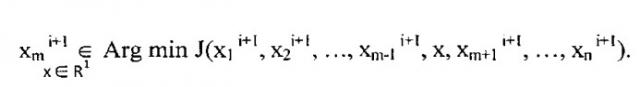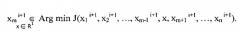2542925 - Способ самоорганизации распределенной многопроцессорной системы

Способ самоорганизации распределенной многопроцессорной системы

Иллюстрации

Показать все

Изобретение относится к области распределенных многопроцессорных систем. Техническим результатом является увеличение производительности распределенной многопроцессорной системы. Способ самоорганизации распределенной многопроцессорной системы заключается в том, что в составе системы выделяют один процессорный элемент, в задачи которого входит отслеживание и управление уровнем производительности системы, определяют набор параметров всех элементов системы, имеющих отношение к оценке производительности, на основе которых строят математическую модель для оценки значения производительности распределенной многопроцессорной системы в виде целевого функционала системы, в процессе функционирования системы получают данные о значении функционала, в случае недостижения функционалом заданного минимально допустимого порогового значения, производят изменение характеристик системы. Для изменения характеристик системы первоначально запускают механизм параметрической самоорганизации, в ходе которого подстраивают значения параметров элементов системы в заданных пределах на основе метода циклического покоординатного спуска, затем, в случае недостижения минимально допустимого порогового значения целевого функционала путем подстройки параметров, запускают механизм функциональной самоорганизации системы, в ходе которой выбирают оптимальные функции для элементов системы из множества реализуемых элементами функций, и затем, в случае недостижения минимально допустимого порогового значения целевого функционала путем изменения функций элементов, изменяют структуру системы, подбирая сначала оптимальные типы элементов, затем реконфигурируя систему, путем определения оптимального местоположения элементов в топологии без изменения их количественного состава, и, наконец, добавляя элементы оптимальных типов в оптимальное местоположение. 4 ил., 1 табл.

Реферат

Изобретение относится к распределенным многопроцессорным системам и может быть использовано для оценки и увеличения производительности такого рода систем.

Под распределенными многопроцессорными системами будем понимать в дальнейшем техническую систему, состоящую из множества процессорных элементов, взаимодействующих между собой посредством каналов связи, и выполняющую определенные задачи. Примерами таких систем могут являться многоядерный сервер обработки и хранения информации, локальная сеть, виртуальные сети, обмен информацией в которых производится через глобальную сеть, и др.

Оценка качества функционирования является одной из важнейших характеристик распределенной многопроцессорной системы, позволяющей сделать выводы о ее производительности и способности к решению поставленных перед ней задач. Кроме того, необходимо иметь методы и средства, позволяющие увеличивать производительность такого рода систем.

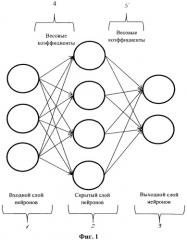
Известен способ оценки и увеличения производительности распределенной многопроцессорной системы (Фиг.1) заключающийся в том, что, анализируя функционирование системы, выделяют несколько параметров, имеющих отношение к комплексной оценке функционирования системы, строят математическую модель системы в виде нейронной сети с минимум одним скрытым слоем нейронов (2). Далее для получения оценки производительности системы на вход сети (1) подают входной вектор значений параметров, а на выходе (3) получают искомую оценку в виде набора выходных параметров. В случае неудовлетворения оценкой качества функционирования системы, нейронная сеть подстраивает весовые коэффициенты (4), (5) в слоях с помощью известных алгоритмов обратного распространения, для того, чтобы выйти на необходимые выходные значения. В дальнейшем подобранные оптимальные значения весов используют в реальной системе как параметры элементов. Недостаток способа заключается в необходимости проведения огромной подготовительной работы по созданию на основе реальной системы ее модели в виде нейронной сети. В случае динамических сред, где число и связи между элементами меняются, в ряде случаев построение единой нейронной модели просто невозможно. Кроме того, в данном способе не анализируются функции системы и ее структура (Pub. № US 2006/0262726 A1 United States, Int. C1. H04L 12/26. Само-изменяющаяся распределенная система / Lieuallen B.R., Samuel G.A., Norton N., Singhal S.K., Manion T.R. - Field 28.04.2006. - Pub date 23.11.2006. - Appl. № 11/413538. - 14 p.).

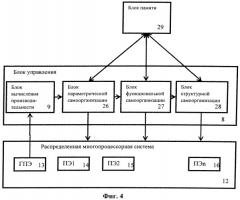
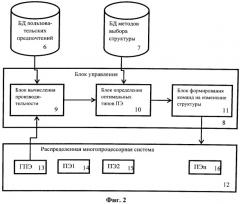
Прототипом заявляемого изобретения является способ оценки и увеличения производительности распределенной многопроцессорной системы (Pub. № US 7913006 B2 United States, Int. C1. G06F 13/00, G06F 9/00, G06F 15/177, G06F 1/24. Самоорганизующаяся параллельная вычислительная система / Hamaoka Y., Ishibashi К., Hayashi H. - Field 06.03.2009. - Pub date 22.03.2011. - Appl. № 12/399, 220. - 25 p.). Функциональная схема системы, реализующей способ, показана на Фиг.2. Способ заключается в том, что в составе системы (12) выделяют один процессорный элемент - главный процессорный элемент (13) - в задачи которого входит отслеживание и управление уровнем производительности системы, определяют набор параметров всех элементов системы (14, 15, 16), имеющих отношение к оценке производительности, на основе которых строят математическую модель для оценки значения производительности распределенной многопроцессорной системы в виде целевого функционала системы, в процессе функционирования системы получают данные о значении функционала в блоке вычисления производительности (9), в случае недостижения функционалом заданного минимально допустимого порогового значения, производят изменение характеристик системы. Изменение характеристик системы производится за счет запуска механизмов самоорганизации, в соответствии с которым все процессорные элементы системы ПЭ1, ПЭ2…ПЭп (14, 15, 16) принадлежат к одному из типов процессных элементов T1, T2…Tm. Тип элемента строго определяет выполняемую элементом функцию. Для улучшения производительности системы на основании выбранного пользователем метода из базы данных методов выбора изменений структуры системы (7) производится определение оптимальной пропорции присутствия элементов типа Ti в системе в блоке определения оптимальных типов (10). Например, если в системе присутствуют 6 элементов (n=6), принадлежащих к одному из 3 типов (m=3), сформированная пропорция может иметь вид 2:1:0, что означает, что система рекомендует изменить структуру таким образом, чтобы в ней было 4 элемента первого типа, 2 - второго и отсутствовали бы третьего. Полученная оптимальная пропорция далее поступает на блок, отвечающий за выработку сигналов на изменение типов элементов (11) и система в зависимости от конкретного применения и исполнения меняет типы некоторых элементов. Описанные действия повторяются циклически или могут быть вызваны различными прерываниями, отражающими изменения состава элементов системы. Кроме того, на основании одного или нескольких критериев оценки производительности системы, хранящихся в базе данных пользовательских предпочтений (6), может быть выбрана другая модель для оценки производительности. В этом случае целевой функционал системы изменяют в соответствии с новой выбранной моделью. Недостатками способа являются низкая масштабируемость в случае присутствия в системе большого числа элементов с большим набором различных типов элементов, отсутствие детальных рекомендаций в общем случае по нахождению оптимальной пропорции, а также присутствие в системе только одного типа самоорганизации - самоорганизации типов элементов - для увеличения ее производительности.

Технический результат заключается в увеличении производительности распределенной многопроцессорной системы.

Для получения указанного технического результата в способе самоорганизации распределенной многопроцессорной системы выделяют один процессорный элемент, в задачи которого входит отслеживание и управление уровнем производительности системы, определяют набор параметров всех элементов системы, имеющих отношение к оценке производительности, на основе которых строят математическую модель для оценки значения производительности распределенной многопроцессорной системы в виде целевого функционала системы, в процессе функционирования системы получают данные о значении функционала, в случае недостижения функционалом заданного минимально допустимого порогового значения производят изменение характеристик системы, для изменения характеристик системы первоначально запускают механизм параметрической самоорганизации, в ходе которого подстраивают значения параметров элементов системы в заданных пределах на основе метода циклического покоординатного спуска, затем, в случае недостижения минимально допустимого порогового значения целевого функционала путем подстройки параметров, запускают механизм функциональной самоорганизации системы, в ходе которой выбирают оптимальные функции для элементов системы из множества реализуемых элементами функций, и затем, в случае недостижения минимально допустимого порогового значения целевого функционала путем изменения функций элементов, изменяют структуру системы, подбирая сначала оптимальные типы элементов, затем реконфигурируя систему, путем определения оптимального местоположения элементов в топологии без изменения их количественного состава, и, наконец, добавляя элементы оптимальных типов в оптимальное местоположение.

На Фиг.3 представлен пример структурной схемы распределенной многопроцессорной системы в виде дерева, вершины которого соответствуют процессорным элементам, а дуги - связям, по которым происходит передача управляющих сигналов и данных. Элементы нижних уровней соответствуют элементарным объектам (ЭО) распределенной многопроцессорной системы (20, 21, 22, 24, 25), которые функционируют по некоторому алгоритму, выполняя некоторую полезную функцию. В качестве элементарного объекта может выступать процессор в многопроцессорной системе, компьютер в составе локальной или глобальной сети, различные автономные устройства и т.д. Элементы-посредники (ЭП) (18, 19, 23) являются элементами более высоких уровней и обобщают полученные результаты функционирования элементов нижних уровней по заранее известному алгоритму, реализуя некоторую функцию свертки

µ=f(el₁, el₂,…, el_p),

где el_i - результат работы элемента i, управляемого текущим ЭП, p - общее число подключенных элементов нижнего уровня к текущему ЭП, f - некоторый оператор (например, оператор сложения), и передают результаты вычисления оценки производительности элементу вышележащего уровня.

Корень дерева (17) формирует значение целевого функционала J для оценки производительности всей системы исходя из полученной информации от элементов первого уровня иерархии и в случае неудовлетворения оценкой корректирует работу системы на основе механизмов самоорганизации.

В случае если для оценки производительности системы необходимо использовать несколько критериев, то для формирования математической модели целевого функционала J используют известные методы: метод главного критерия, метод линейной свертки частных критериев в один и др.

После того как в корне системы задана функция для оценки общей производительности системы, в некоторые моменты времени производят ее замеры J_t и сравнение с некоторым пороговым минимально допустимым значением J_min. Если J_t≥J_min, то считают, что производительность системы находится на приемлемом уровне, никаких действий предпринимать не следует. Иначе, для увеличения производительности системы запускают механизмы самоорганизации в системе. Начинают с параметрической самоорганизации, в ходе которой увеличение производительности может быть достигнуто подстройкой некоторых параметров элементов системы. Если после подстройки параметров удается достичь выполнения неравенства J_t≥J_min, считается, что параметрическая самоорганизация увенчалась успехом, система продолжает функционировать с новыми значениями параметров. Иначе, в случае невозможности подстройки параметров для выполнения неравенства, запускают механизм функциональной самоорганизации, в ходе которого увеличение производительности системы может быть достигнуто за счет изменения реализуемых элементами функций. После каждого изменения функции запускают механизм подбора параметров. В случае, если изменение функций и параметров приводит к выполнению неравенства J_t≥J_min, считается, что функциональная самоорганизация увенчалась успехом, и система продолжает функционировать с новыми реализуемыми функциями и их параметрами. Иначе запускают механизм структурной самоорганизации, в ходе которой изменяют типы элементов в системе, их местоположение и количественный состав. Для каждого изменения структуры системы производят подбор функций элементов и их параметров. В случае, если изменением структуры системы удается достичь выполнения неравенства J_t≥J_min, считается, что структурная самоорганизация увенчалась успехом, и система продолжает функционировать с новой структурой, реализуемыми функциями и их параметрами. Если и в процессе структурной самоорганизации не удается достичь выполнения неравенства J_t≥J_min, делают вывод о невозможности достижения данной распределенной многопроцессорной системой требуемого уровня производительности. В случае наличия в корне системы блока, накапливающего результаты проведенных процессов самоорганизаций, эти результаты сначала анализируют и принимают более оптимальное решение о необходимости того или иного этапа самоорганизации. Например, может быть сделан вывод о нецелесообразности выполнения параметрической самоорганизации, в результате сразу переходят к изменению функций элементов системы, что ускоряет время выполнения способа.

Далее детально рассматривается каждый из этапов самоорганизации для увеличения производительности распределенной многопроцессорной системы.

На первом этапе - этапе параметрической самоорганизации - первоначально определяют набор всех параметров, имеющих отношение к вычислению производительности системы. Производительность каждого элементарного объекта выражают некоторой функцией f_k, зависящей от выбранного набора параметров. Природа параметров может быть принципиально различна. Это могут быть какие-либо его ресурсы, число операций в единицу времени, качество обработки данных и т.д. Функция может состоять из любой комбинации основных элементарных математических функций (sin, cos, ln и т.д.) и операций, кроме того, процессы в системе происходят в реальном времени, поэтому все функции являются также функциями времени.

Реализация элементом функции производительности, в общем, всегда связана с наличием некоторых ограничений, налагаемых на ее параметры. Наиболее часто такие ограничения имеют вид:

a_i≤x_i≤b_i,

где a_i, b_i∈R, хотя возможны и более сложные нелинейные ограничения. Для исключения указанных ограничений используют операцию замены переменных, заключающуюся в замене переменных в исходной функции в соответствии с таблицей 1.

Таблица 1
Замена переменных для снятия ограничений на параметры
Ограничение	Преобразование
x_i>a_i	x_i=a_i+exp(z_i)
x_i>x_j	x i = a i + z i 2
x_i>x_j, i≠j	x_j=z_j, x i = z j + z i 2
a_i≤x_i≤b_i	x_i=b_i+(a_i-b_i)*sin²z_i
x_i=0.5(a_i+b_i)+0.5(b_i-a_i)*sinz_i
a_i<x_i<b_i	x_i=b_i+(a_i-b_i)(1/π)arctgz_i
x_i=b_i+(a_i-b_i)*exp(z_i)/(1+exp(z_i))
a≤x_i≤b	x_j=b+(a-b)*sin²z_j
a≤x_j≤b x_i>x_j, i≠j	x_i=b+(a-b)sin²z_jsin²z_i
a<x_i<b	x_j=b+(a-b)(1/π)arctgz_j
a<x_j<b x_i>x_j, i≠j	x_i=b+(a-b)(1/π²)arctgz_i*arctgz_i
a_i(x_j)≤x_i≤b_i(x_j)	x_j=z_j
i≠j	x_i=b_i(z_j)+(a_i(z_j)-b_i(z_j))*sin²z_i
a_i(x_k)≤x_i≤b_i(x_j)	x_j=z_j x_k=z_k
i≠j, i≠k	x_i=b_i(z_j)+(a_i(z_k)-b_i(z_j))*sin²z_i

Параметры функций f_k могут носить как детерминированный, так и стохастический характер. Во втором случае функция f_k может быть представлена в виде f_k=F(x,ξ), где ξ - неопределенный вектор. Выделяют две основные ситуации, характерные для распределенных многопроцессорных систем и отражающие природу вектора ξ:

- ξ - случайный вектор с известным законом распределения;

- вектор ξ изменяется неизвестным образом, но не носит случайный характер, либо статистические характеристики ξ оказываются неизвестными.

При наличии неопределенности первого рода используют математическое ожидание (МО) случайного вектора ξ. Функция f_k принимает в данном случае вид

f_k=F(x,ξ′)

Значение ξ 0 ' в начале работы системы выбирается и устанавливается в соответствии с экспертными оценками, а затем, в процессе функционирования, уточняется по мере накопления системой информации:

где ξ_i - значения вектора ξ в i-й момент снятия данных.

При наличии неопределенности второго рода указанный подход в ряде случаев оказывается неэффективным из-за невозможности предсказания значения МО вектора ξ. B этом случае применяют расчет на наихудший случай, используя так называемый принцип «гарантированного результата». Функция f_k принимает вид:

f_k=F(x, max(ξ)), или

f_k=F(x, min(ξ)).

После того как все параметры определены и сформирован целевой функционал для оценки производительности, проводят операцию параметрической оптимизации. Операцию параметрической оптимизации ставят как многокритериальную операцию параметрической оптимизации с ограничениями и формулируют следующим образом:

f_i(x)→min(x), i∈[l:k], x∈D⊂Rⁿ,

где D={х∈Rⁿ|g_i(x,δ)≤0, i∈[l:m]; g_i(x,δ)=0, i∈[m+l:s]} - множество допустимых решений; x={x₁, …, x_z} - вектор входных параметров, y={y₁, …, y_k} - вектор критериальных выходных параметров; δ={δ₁, …, δ_w} - вектор внешних параметров, характеризующих неопределенность обстановки. В пределах множества D выполняются прямые, функциональные и критериальные ограничения, представленные в виде общей системы неравенств и равенств. Прямые ограничения накладываются непосредственно на компоненты вектора входных параметров; функциональные ограничения включают условия работоспособности, имеющие принципиальное значение при оценке правильности функционирования объекта оптимизации, выполнение функциональных ограничений с большим запасом обычно не требуется, важно просто обеспечить их выполнение; критериальные ограничения отражают требования к характеристикам объекта оптимизации, их основное отличие от функциональных ограничений состоит в том, что для критериальных ограничений необходимо добиваться выполнения соответствующих им неравенств с максимальным запасом.

Этап параметрической самоорганизации осуществляют одним из нескольких методов параметрической оптимизации, наиболее универсальным из которых является метод циклического покоординатного спуска (ЦПС). Так как необходимо подобрать такой набор параметров x, который обеспечит выполнение условия J_t≥J_min, то при каждом проходе метода осуществляют проверку выполнения данного неравенства, и, если оно выполнено, сохраняют необходимые данные об изменениях параметров и работу этапа прекращают. Метод ЦПС имеет высокую надежность по отношению к различным сбойным ситуациям, а также прост в процессе подготовки задачи к моделированию на компьютере, т.к. имеет нулевой порядок, т.е. не требует включения в вычислительную схему информации о производных от минимизируемого функционала.

Для построения минимизирующей последовательности {x^k} функционала J(x) переход от вектора xⁱ к вектору xⁱ⁺¹ по методу ЦПС проводят следующим образом: для m∈[l:n] компонента x m i + 1 определяется как:

Вначале задают вектор начальных шагов h=(h₁,…, h_n) продвижений из точки x в направлении координатных ортов e¹, e², …, eⁿ. Далее шаги h_i модифицируют от итерации к итерации. Если выполняется неравенство J(x+h_ieⁱ)<J(x), то текущую точку x заменяют на x+h_ieⁱ, а величину h_i утраивают: h_i=3h_i. После этого осуществляют переход к следующему номеру i. Если J(x+h_ieⁱ)>J(x), то производят умножение h_i на -0,5 и также осуществляют переход к следующему координатному орту. Таким образом, метод адаптируется к конкретным условиям оптимизации за счет изменения величин и знаков шагов. Если начальные значения шагов были выбраны неудачно, то они быстро скорректируются до необходимых значений.

Для уменьшения времени выполнения метода может быть использована операция сравнения изменений параметров, при которой по завершении каждого этапа параметрической самоорганизации сохраняют вектор x ' = ( x 1 ' , … , x n ' ) , где x i ' = | x i − x i 0 | / min ( x i ; x i 0 ) . При последующих запусках этапа параметрической самоорганизации изменение составляющих вектора x производят в порядке убывания значений вектора x′, который соответствует убыванию величины, показывающей, во сколько раз изменился каждый параметр после предыдущего этапа параметрической самоорганизации.

Далее рассмотрим реализацию этапа функциональной самоорганизации. В общем случае, ЭО может быть отнесен к определенному типу ЭО. Обозначим множество всех типов ЭО в системе S как T_s:

T_s={T_1,s, T_2,s, …, T_n,s},

где n - число различных типов ЭО в системе S. Отметим, что тип ЭО определяет соответствующий набор характерных параметров и множество реализуемых ЭО функций.

ЭО типа i функционирует по одному из заранее предусмотренных алгоритмов. Алгоритм для каждой конкретной системы может быть задан по-разному и во многих случаях является достаточно сложным и даже «закрытым». Однако нас не интересуют детали функционирования объекта, и мы не заботимся о воспроизведении точной модели его работы. Для нас важна только выходная функция данного объекта, имеющая отношение к формированию целевого функционала для оценки производительности системы. ЭО типа i в каждый момент времени реализует выходную функцию f_k,i∈F_i, где F_i - набор функций, реализуемых ЭО типа i:

F_i={F_1,i, F_2,I,…, F_mi},

где m - число различных функций, которые может реализовать объект типа i.

В общем случае, влияние ЭО на целевую функцию может выражаться не одной, а сразу несколькими независимыми функциями:

где p - общее число функций ЭО, влияющих на формирование целевого функционала системы J(x). Каждая функция f k , i j зависит от набора параметров P, характеризующих ЭО типа i:

где q - число параметров ЭО типа i.

На этапе функциональной самоорганизации подбирают функции, которые реализуют объекты системы для достижения нужного уровня производительности, а не параметры. Исходя из того, что исследование сложной функции на оптимум с параметрами, изменяющимися в произвольном диапазоне, затруднительно, для реализации этапа используют следующие операции.

Первоначально выбирают первую по порядку функцию, которую реализует лист системы, и для нее подбирают оптимальные параметры, т.е. запускают этап параметрической самоорганизации. Если после выполнения этапа параметрической самоорганизации необходимые результаты не достигнуты, выбирают следующую по порядку функцию, которую может реализовать данный элемент, и для нее запускают этап параметрической самоорганизации. Если все функции элемента перебраны, а функционал системы не достиг нужного значения, осуществляют переход к следующему листовому элементу, и описанные операции повторяются.

Для ускорения выполнения этапа функциональной самоорганизации используют операцию выбора оптимальной функции, основанную на использовании предыдущего опыта, при которой, единожды перебрав все функции элемента данного типа, определяется, какая из них дает максимум прироста выходной функции системы. Таким образом, при последующих запусках данного этапа самоорганизации, заранее известно, какая функция даст оптимум для данного типа объектов. Перебор всех функций проводится один раз для всех типов объектов, находящихся в системе. На основе информации об оптимальной функции функциональную самоорганизацию осуществляют при последующих запусках за один шаг, выбирая для каждого элемента найденную оптимальную функцию.

На этапе структурной самоорганизации топология дерева системы, а также количество элементов могут измениться. Структурная самоорганизация является более мощным средством адаптации, чем параметрическая или функциональная, но требует гораздо больших затрат на реализацию.

Очевидно, что добавление новых объектов связано с некоторыми финансовыми и другими затратами. Поэтому на этапе структурной самоорганизации в систему вводят некоторый эквивалент стоимости при добавлении новых элементов. В результате каждому из типов элементов в системе ставят в соответствие число, называемое далее стоимостью (price).

В связи с тем, что элементы-посредники выполняют функцию свертки результатов значений нижестоящих элементов, как правило, с ростом количества дочерних элементов растет и значение в родительском элементе-посреднике. Таким образом, можно выделить из всех элементов-посредников тот, добавление элементарного объекта к которому даст максимальный прирост целевого функционала, и на последующих шагах самоорганизации добавлять элементы только к этому элементу-посреднику. Однако это приведет к неограниченному возрастанию потомков данного элемента-посредника.

Очевидно, что в реальных системах такая ситуация является недопустимой. В связи с этим в систему вводят ограничения на количество дочерних узлов у каждого родительского. Каждому типу ставят в соответствие количество слотов (slots) - некоторое неотрицательное целое число, ограничивающее сверху допустимое количество дочерних узлов-элементов для данного типа. Количество слотов элементарного объекта равно нулю. Именно количество слотов, а не количество существующих дочерних узлов характеризует узел как элемент-посредник или элементарный объект. Так, в частном случае элемент-посредник может быть листом и не иметь детей, но от этого не становится элементарным объектом.

Структурная самоорганизация включает в себя три операции: подбор оптимальных типов для листовых элементов дерева системы (типовая самоорганизация), реконфигурация дерева на уровне элементарных объектов (изменяется топология дерева без изменения состава элементов) и добавление новых элементов в систему.

Первоначально запускают операцию подбора оптимальных типов - типовую самоорганизацию. Далее, если система по-прежнему не удовлетворяет поставленным критериям, осуществляют реконфигурацию системы. Наконец, в систему включают новые элементы. Если и последней операцией не удается достичь нужного значения целевого функционала, работа системы останавливается и выдается запрос об изменении целей функционирования.

Далее приводится детальное описание трех операций этапа структурной самоорганизации. Первой является типовая самоорганизация, в ходе которой подбираются оптимальные типы для элементов системы. Именно тип элемента определяет набор функций, которые может реализовывать элемент системы.

Подбор оптимального типа для каждого элемента системы является переборной задачей и обладает рядом особенностей. Важно помнить, что тип элемента не только определяет набор функций, реализуемых данным узлом, но и показывает, является ли данный узел элементарным объектом или элементом-посредником. Так, элементарный объект может быть только листом дерева, в то время как элемент-посредник может занимать любое положение (кроме корня), однако способен влиять на целевой функционал только при условии наличия дочерних узлов.

Таким образом, при переборе типов важно не допустить ситуации, когда некоторый, имеющий дочерние узлы элемент-посредник получит тип элементарного объекта, так как в таком случае работоспособность системы нарушается. С другой стороны, элементарный объект может сменить тип на тип элемента-посредника, однако, очевидно, в таком случае прирост целевого функционала системы будет отрицателен, так как висячий (не имеющий дочерних узлов) элемент-посредник не оказывает влияния на целевой функционал.

На основании вышеизложенных ограничений типовую самоорганизацию проводят только на уровне элементарных объектов. Подобное ограничение существенно ускоряет время выполнения операции, сокращая количество вариантов перебора. Исключением является элемент-посредник, не имеющий дочерних узлов. Такой элемент-посредник не оказывает влияния на систему и в случае замены его на элементарный объект возможно получить некоторый положительный прирост целевого функционала.

В связи с этим под типовой самоорганизацией понимают процесс самоорганизации, в результате которого для каждого листа дерева системы подбирается оптимальный тип.

В ходе типовой самоорганизации осуществляют обход дерева системы, при этом для каждого элемента-листа осуществляют перебор всех возможных типов. После изменения типа одного объекта осуществляют запуск сначала параметрической, а в случае ее неэффективности - функциональной, самоорганизации. После того как перебраны все возможные типы, в качестве конечного типа для элемента выбирают тот тип, при котором значение в данном листе является максимальным по сравнению со значениями при других типах.

После того как выбран оптимальный тип для одного элемента-листа, осуществляют проверку соответствия системы поставленным критериям. Если система удовлетворяет таковым, этап структурной самоорганизации считается успешным и самоорганизация завершается. В случае, если система не удовлетворяет поставленным критериям, переходят к следующему элементу системы. В случае, если для всех листов дерева подобраны оптимальные типы, а система по-прежнему не удовлетворяет поставленным критериям, типовая самоорганизация считается неуспешной.

На основании вышеизложенного видно, что в результате типовой самоорганизации может оказаться, что не всем листам будет подобран оптимальный тип. Такой подход увеличивает быстродействие операции, существенно сокращая мощность множества вариантов перебора, однако не гарантирует, что полученный на этапе типовой самоорганизации прирост целевого функционала будет максимально возможным.

В случае, если типовая самоорганизация не принесла успеха, переходят к запуску операции реконфигурации системы, в ходе которой производится изменение местоположения элементов в иерархии. Реконфигурацию проводят в несколько этапов, на каждом из которых осуществляют перенос одного элементарного объекта на более выгодное с точки зрения увеличения целевого функционала производительности место. Реконфигурацию заканчивают, если полученная система удовлетворяет поставленным критериям или анализ функционирования системы показывает, что ее дальнейшая оптимизация невозможна.

На каждом из этапов реконфигурации для каждого типа элементарного объекта, представленного в системе одним или несколькими элементами, определяют два положения: «наихудший» элемент данного типа, существующий в системе (под его положением подразумевается родительский элемент данного элементарного объекта) и «наилучшее» место для добавления элемента данного типа в систему.

Под «наихудшим» элементом типа понимают такой элемент, при удалении которого из системы целевой функционал имеет большее значение, чем при удалении любого другого элемента данного типа.

Под «наилучшим» местом понимают такой элемент-посредник, при добавлении элементарного объекта заданного типа к которому целевой функционал будет больше, чем при добавлении элементарного объекта данного типа к любому другому элементу-посреднику. Важно, что добавление объекта в качестве дочернего узла того или иного элемента-посредника возможно лишь при наличии у выбранного элемента-посредника свободных слотов.

Для определения «наихудшего» элемента каждого типа осуществляют обход дерева, т.е. прохождение по всем элементам элементов дерева. Если текущий элемент дерева является элементом-посредником и среди его дочерних узлов имеется хотя бы один элемент необходимого типа, любой (первый найденный) дочерний узел данного типа временно удаляют из системы. После этого проводят подсчет целевого функционала полученной системы и его оценку, а затем удаленный элемент возвращают в систему.

Для определения «наилучшего» места для добавления элемента осуществляют повторный обход дерева. Если текущий элемент дерева является элементом-посредником и имеет свободные слоты, осуществляют временное добавление к нему элемента заданного типа с начальными параметрами - в качестве функции элемента используют первую функцию из списка функций данного типа, все параметры сбрасывают до минимально допустимых значений. Далее запускают функциональную самоорганизацию, которая осуществляет подстройку функций новой системы. Заметим также, что на каждом шаге функциональной самоорганизации запускают параметрическую, подбирающую оптимальные параметры для выбранных функций. По окончании работы функциональной самоорганизации элементы системы содержат оптимальные для данной структуры функции и параметры. Производят подсчет и оценку функционала производительности полученной системы и удаление временного объекта. После удаления элемента система не возвращается к своему исходному состоянию, так как функциональная и структурная самоорганизация необратимы. Однако это не имеет значения, так как для реконфигурации важна только структура системы, а параметры и функции подбирают заново на каждом шаге с целью получения максимального выходного функционала.

Таким образом, для каждого типа находят «наихудший» элемент (и значение функционала при удалении его из системы), а также лучшую позицию для добавления элемента данного типа (и соответствующее значение функционала). После этого определяют тип, перемещение элемента которого даст максимальный прирост функционала системы. Выбирают тот тип, для которого значение выражения J_b-J_w является максимальным, где J_b - максимальное значение функционала при добавлении элемента заданного типа в систему, J_w - максимальное значение функционала при удалении элемента заданного типа из системы.

Если максимальное значение выражения неотрицательно, осуществляют удаление «худшего» элемента соответствующего типа и добавление элемента соответствующего типа на «лучшее место». Если после проведенного этапа реконфигурации система по-прежнему не удовлетворяет поставленным критериям, запускают повторный этап реконфигурации, и описанные действия повторяются.

Отрицательное значение выражения J_b-J_w для всех типов говорит о том, что достигнута оптимальная структура для данного набора элементов системы и дальнейшая реконфигурация нерациональна.

Если реконфигурация не увенчалась успехом, выполняют операцию добавления элементов системы с целью получения максимального прироста функционала производительности. Отметим, что этап структурной самоорганизации запускают после параметрической и функциональной при условии, что они не смогли скорректировать систему так, чтобы она удовлетворяла поставленным критериям. Тогда к началу этапа структурной самоорганизации функции и параметры элементов системы являются оптимальными для существующей структуры, т.е. каждый объект дает положительный прирост целевого функционала и при удалении элемента из системы значение функционала уменьшится. Исходя из этого можно говорить о нецелесообразности удаления существующих элементов из системы.

Операцию добавления разбивают на несколько этапов, на каждом из которых добавляют один элемент. Если по окончании этапа система по-прежнему не удовлетворяет поставленным критериям, проводят следующий этап добавления, в противном случае самоорганизация завершается.

Важнейшим моментом при добавлении элемента в систему является определение типа этого элемента. При этом реализуемая функция, а также ее параметры не являются принципиальными, так как будут впоследствии скорректированы.

Добавление в систему элементарного объекта

Способ самоорганизации распределенной многопроцессорной системы

Патент 2542925