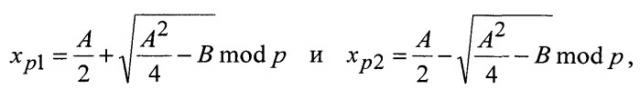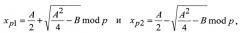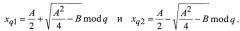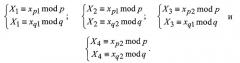Способ шифрования сообщения, представленного в виде многоразрядного двоичного числа

Способ шифрования сообщения, представленного в виде многоразрядного двоичного числа

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области информационной безопасности телекоммуникационных систем и, в частности, может быть использовано в криптографических системах, обеспечивающих конфиденциальность сообщений, передаваемых по открытым каналам связи.

Известен способ шифрования путем формирования секретного ключа, генерации ключевого потока в виде последовательности битов, зависящих от секретного ключа, и сложения текущих битов ключевого потока с текущими битами передаваемого сообщения [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. С.-Петербург, Лань, 2000. - 218 с.; см. с.88-89]. Недостатком этого способа шифрования является необходимость синхронизации ключевого потока и потока данных.

Также известен способ шифрования, включающий генерацию 56-битового секретного ключа, формирование сообщения M в виде 64-битовой строки, генерацию криптограммы, представляющей собой 64-битовую строку, в зависимости от секретного ключа [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. С.-Петербург, Лань, 2000. - 218 с.; см. с.68-73]. При этом генерация криптограммы осуществляется путем разбиения сообщения M на две 32-битовые строки и поочередное преобразование 32-битовых строк в зависимости от секретного ключа. Недостатком этого способа является малый размер секретного ключа, что не обеспечивает криптостойкости, соответствующей современным требованиям.

Толкование терминов, используемых в описании, приведено в Приложении 1

Также известен способ шифрования сообщения M, представленного в виде битовой строки, описанный в патенте США №4424414 [Hellman M.E., Pohlig S.C. Exponentiation Cryptographic Apparatus and Method // U.S. Patent #4,424,414. Jan.3, 1984] и в книге [Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. - М:. Издательство ТРИУМФ, 2002. - 815 с.; см. с.577-578]. Ближайший способ-аналог (прототип) включает следующие действия:

1. Генерируют простое многоразрядное двоичное число (МДЧ) p.

2. Генерируют секретный ключ в в виде двух МДЧ e и d, удовлетворяющих условию ed≡1 mod p-1

3. Формируют криптограмму в виде МДЧ C по формуле C=M^e mod p.

4. Восстанавливают сообщение M из криптограммы C по формуле M=C^d mod p.

Наиболее близким по своей технической сущности к заявленному способу шифрования сообщения M, представленного в виде МДЧ, является известный способ шифрования, включающий генерацию секретного ключа в виде двух больших простых МДЧ p и q, генерацию открытого ключа в виде МДЧ n, формирование криптограммы в виде МДЧ C по формуле C=M² mod n [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С.-Петербург. Петербург - БХВ, 2010. - 304 с.; см. с.78] и восстановление сообщения M из криптограммы C путем вычисления квадратных корней из криптограммы по модулю n, а именно по формуле M = C   mod   n , из которой вычисляются четыре различных корня, одним из которых является сообщение M. Недостатком этого способа шифрования является то, что данный способ шифрования не обеспечивает достаточной стойкости при шифровании сравнительно коротких сообщений, например сообщений, размер которых не превышает половины размера МДЧ n. Этот недостаток связан с тем, что извлечение квадратных корней из криптограмм, полученных путем возведения коротких сообщений в квадрат, может быть выполнен сравнительно легко без знания разложения МДЧ n на простые множители p и q, являющиеся элементами секретного ключа.

Задачей заявленного нового технического решения является разработка способа шифрования, в котором устраняется возможности восстановления сообщения из криптограмм, полученных путем шифрования коротких сообщений, без знания разложения МДЧ n на простые множители p и q.

Техническим результатом нового способа шифрования сообщения M, представленного в виде МДЧ, является повышение уровня защищенности информации при шифровании коротких сообщений.

Указанный технический результат достигается тем, что в способе шифрования сообщения M, представленного в виде МДЧ, заключающемся в том, что генерируют секретный ключ (p, q) в виде двух простых многоразрядных двоичных чисел p и q, генерируют открытый ключ в виде многоразрядного двоичного числа n=pq, формируют криптограмму С в зависимости от сообщения M и открытого ключа n и восстанавливают сообщение M из криптограммы C по секретному ключу (p, q),

новым является то, что дополнительно генерируют вспомогательное МДЧ R<n, криптограмму C формируют в виде пары (A, B) многоразрядных двоичных чисел A и B в зависимости от сообщения M, открытого ключа n и МДЧ R, а восстанавливают сообщение M путем решения уравнения x²-Ax+B=0 mod n относительно неизвестного x и вычисления сообщения M из одного из решений указанного уравнения.

Генерация вспомогательного МДЧ R<n, имеющего разрядность, примерно равную разрядности МДЧ n, устраняет возможность нахождения решений уравнения X²-Ax+B=0 mod n без знания разложения МДЧ n на простые множители p и q для сообщений M, представленных в виде МДЧ любого размера, включая короткие сообщения, например размером от 1 до 500 бит.

Новым также является то, что криптограмму C формируют в виде пары (A, B) МДЧ A и B, генерируемых по формулам A=(R+n-M-1) mod n и B=R(n-M-1) mod n.

Генерация МДЧ A и B по формулам A=(R+n-M-1) mod n и B=R(n-M-1) mod n обеспечивает то, что уравнение x²-Ax+B=0 mod n в качестве своих решений имеет МДЧ x₁=R и МДЧ x₂=n-M-1 mod n, и сообщение вычисляется по формуле M=n-x₂-1 mod n.

Новым также является и то, что криптограмму C формируют в виде пары (A, B) МДЧ A и B, генерируемых по формулам A=(2R-M) mod n и B=R(R-M) mod n.

Генерация МДЧ A и B по формулам A=(2R-M) mod n и B=R(R-M) mod n обеспечивает то, что уравнение x²-Ax+B=0 mod n в качестве своих решений имеет МДЧ x₁=R и МДЧ x₂=R-M mod n и сообщение вычисляется по формуле M=R-x₂ mod n.

Новым является и то, что дополнительно генерируют вспомогательное МДЧ R<n путем генерации вспомогательного сообщения T и вычисления R по формуле R=(n-T) mod n.

Генерация вспомогательного МДЧ R<n путем генерации вспомогательного сообщения T и вычисления R по формуле R=(n-T)² mod n позволяет осуществить совместное шифрование двух сообщений, которые восстанавливаются из криптограммы C=(A, B) путем решения уравнения x²-Ax+B=0 mod n относительно неизвестного x и вычисления сообщения M из одного из решений, а сообщения T - из другого решения. Эта возможность реализуется путем генерации МДЧ A и B по формулам A=(R+M) mod n и В=RM mod n. В случае таких значений МДЧ A и B уравнение x²-Ax+B=0 mod n в качестве своих решений имеет МДЧ x₁=R и МДЧ x₂=M и сообщение T вычисляется по формуле T = n − x 1   mod   n , а сообщение M - по формуле M=x₂.

Изобретательский замысел заявленного нового технического решения состоит в дополнительной генерации вспомогательного МДЧ R<n достаточно большого размера и формировании криптограммы C в виде пары МДЧ A и B, являющихся коэффициентами уравнения x²-Ax+B=0 mod n и зависящих как от сообщения M, так и от МДЧ R. Это позволяет восстановить сообщение M путем решения указанного уравнения и вычисления сообщения M из одного из его решений. Зависимость решений от МДЧ R устраняет возможность восстановления сообщений M малого размера без знания разложении числа n. Благодаря указанной новой совокупности существенных признаков достигнут сформулированный изобретательский замысел.

Проведенный анализ уровня техники позволил установить, что в известных источниках информации аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного изобретения условию патентоспособности «новизна». Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».

Корректность заявленного способа шифрования сообщения M, представленного в виде МДЧ, обеспечивается тем, что многочлен второй степени x²-Ax+B (mod n), корнями которого являются МДЧ x₁ и x₂, может быть представлен в виде произведения (x-x₁)(x-x₂), т.е. имеет место

x²-Ax+B=(x-x₁)(x-x²)=x²-(x₁+x₂)x+x₁x₂ (mod n)

следовательно, A=(x₁+x₂) mod n и B=x1x₂ mod n. Поэтому, если встроить сообщение M и дополнительно генерируемое МДЧ R в корни уравнения x²-Ax+B=0 mod n таким образом, что из корней x₁ и x₂ легко можно вычислить M и R, то восстановление сообщения M из криптограммы можно выполнить путем решения указанного уравнения и вычисления M из одного из корней. Таким образом, корни x₁ и x₂ вычисляются по значениям M и R, а криптограмма C формируется в виде пары МДЧ (A, B) по формулам A=(x₁+x₂) mod n и B=x₁x₂ mod n. Криптограмма задает такие коэффициенты указанного уравнения второй степени, при которых МДЧ x₁ и x₂ являются решениями этого уравнения. Решение уравнения с коэффициентами, заданными криптограммой, позволит найти МДЧ x₁ и x₂ и вычислить из последних сообщение M и МДЧ R.

Решение уравнения x²-Ax+B=0 mod n выполняется по секретному ключу (p, q) следующим путем. Решаются следующие два уравнения: x²-Ax+B=0 mod p и x²-Ax+B=0 mod q, каждое из которых имеет два корня. Пусть корнями первого уравнения являются следующие два значения:

а корнями второго - следующие:

Вычислительно эффективные алгоритмы извлечения квадратных корней по простому модулю описаны, например, в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С.-Петербург. Петербург - БХВ, 2010. - 304 с.; см. с.25-29]. Четыре корня X₁, X₂, X₃ и X₄ уравнения x²-Ax+B=0 mod n находятся как решения следующих четырех систем линейных сравнений

В соответствии с китайской теоремой об остатках [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С.-Петербург. Петербург - БХВ, 2010. - 304 с.; см. с.15-16] решениями этих четырех систем сравнений являются следующие четыре МДЧ:

X₁=(x_p1q(q^-1 mod p)+x_q1p(p^-1 mod q))mod n;

X₂=(x_p1q(q^-1 mod p)+x_q2p(p^-1 mod q))mod n;

X₃=(x_p2q(q^-1 mod p)+x_q1p(p^-1 mod q))mod n;

X₄=(x_p2q(q^-1 mod p)+x_q2p(p^-1 mod q))mod n.

По значениям корней X₁, X₂, X₃, и X₄ вычисляются четыре различных МДЧ M₁, M₂, M₃ и M₄, соответственно. При этом одно из МДЧ M₁, M₂, M₃, и M₄, например M₄, соответствует осмысленному сообщению M, представленному в виде МДЧ, т.е. из криптограммы (A, B) восстанавливается сообщение M=M₄.

Рассмотрим частные примеры реализации заявленного способа шифрования сообщения M, представленного в виде МДЧ.

Пример 1

Данный пример иллюстрирует реализацию заявленного способа по п.2 формулы изобретения. В данном частном варианте реализации способа выполняются следующие действия:

1. Генерируют секретный ключ (p, q) в виде двух простых 512-разрядных двоичных чисел p и q.

2. Генерируют открытый ключ в виде МДЧ n=pq.

3. Формируют криптограмму C в виде пары (A, B) МДЧ A и B в зависимости от сообщения M и открытого ключа n путем выполнения следующих действий:

3.1. Генерируют вспомогательное МДЧ R<n в виде случайного 1022-разрядного двоичного числа R.

3.2. Генерируют МДЧ A по формуле A=(R+n-M-1) mod n.

3.3. Генерируют МДЧ В по формуле B=R(n-M-1) mod n.

4. Восстанавливают сообщение M из криптограммы C по секретному ключу (p, q) путем выполнения следующих действий:

4.1. Вычисляют четыре решения уравнения второй степени x²-Ax+B=0 mod n в виде МДЧ X₁, X₂, X₃ и X₄.

4.2. Вычисляют четыре МДЧ M₁, M₂, M₃, и M₄ по формуле

Mi=(n-X_i-1) mod n, где i=1, 2, 3 и 4.

4.3. Отбрасывают три случайных МДЧ, например МДЧ M₁, M₂ и M₃, и в качестве восстановленного сообщения M берут осмысленное сообщение, представленное МДЧ M₄, т.е. M=M₄.

Пример 2

Данный пример иллюстрирует реализацию заявленного способа по п.3 формулы изобретения. В данном частном варианте реализации способа выполняются следующие действия:

1. Генерируют секретный ключ (p, q) в виде двух простых 768-разрядных двоичных чисел p и q.

2. Генерируют открытый ключ в виде МДЧ n=pq.

3. Формируют криптограмму C=(A, B) в виде пары МДЧ A и B в зависимости от сообщения M и открытого ключа n путем выполнения следующих действий:

3.1. Генерируют вспомогательное МДЧ R<n в виде случайного 1534-разрядного двоичного числа R.

3.2. Генерируют МДЧ A по формуле A=(2R-M) mod n.

3.3. Генерируют МДЧ В по формуле В=R(R-M) mod n.

4. Восстанавливают сообщение M из криптограммы C по секретному ключу (p, q) путем выполнения следующих действий:

4.1. Вычисляют четыре решения уравнения второй степени x²-Ax+B=0 mod n в виде МДЧ X₁, X₂, X₃ и X₄.

4.2. Вычисляют четыре МДЧ M₁, M₂, M₃, и M₄ по формуле

M=(2X_i-A) mod n, где i=1, 2, 3 и 4.

4.3. Отбрасывают три случайных МДЧ, например МДЧ M₁, M₃, и M₄, и в качестве восстановленного сообщения M берут осмысленное сообщение, представленное МДЧ M₃, т.е. M=M₄.

Пример 3

Данный пример иллюстрирует реализацию заявленного способа по п. 4 формулы изобретения. B данном частном варианте реализации способа криптограмма формируется в зависимости от двух независимых сообщений - сообщения M и вспомогательного сообщения T, которые восстанавливаются из криптограммы. В данном примере выполняются следующие действия:

1. Генерируют секретный ключ (p, q) в виде двух простых 1024-разрядных двоичных чисел p и q.

2. Генерируют открытый ключ в виде МДЧ n=pq.

3. Формируют криптограмму C=(A, B) в виде пары МДЧ A и B в зависимости от сообщения M и открытого ключа n путем выполнения следующих действий:

3.1. Генерируют вспомогательное МДЧ R<n в виде случайного 2046-разрядного двоичного числа R, для чего

3.1.1. Генерируют вспомогательное сообщение T.

3.1.2. Вычисляют МДЧ R по формуле R=(n-T)² mod n.

3.2. Генерируют МДЧ A по формуле A=(2R-M) mod n.

3.3. Генерируют МДЧ B по формуле B=R(R-M) mod n.

4. Восстанавливают сообщение M из криптограммы C по секретному ключу (p, q) путем выполнения следующих действий:

4.1. Вычисляют четыре решения уравнения второй степени x²-Ax+B=0 mod n в виде МДЧ X₁, X₂, X₃, и X₄.

4.2. Вычисляют четыре МДЧ M₁, M₂, M₃, и M₄, по формуле

M_i=(2X_i-A) mod n, где i=1, 2, 3 и 4.

4.3. Отбрасывают три случайных МДЧ, например МДЧ M₁, M₃, и M₄, и в качестве восстановленного сообщения M берут осмысленное сообщение, представленное МДЧ M₃, т.е. M=M₃.

5. Восстанавливают вспомогательное сообщение T из криптограммы C по секретному ключу (p, q) путем выполнения следующих действий:

4.1. Вычисляют значение МДЧ R=(M+A)/2 mod n 0 mod n.

4.2. Вычисляют четыре МДЧ U₁, U₂, U₃ и U₄, являющихся корнями второй степени из МДЧ R, после чего вычисляют МДЧ T₁, T₂, T₃, и T₄ по следующей формуле

T_i=n-U_i mod n, где i=1, 2, 3 и 4.

4.3. Отбрасывают три случайных МДЧ, например МДЧ T₁, T₃, и T₄, и в качестве восстановленного вспомогательного сообщения T берут осмысленное сообщение, представленное МДЧ T₂, т.е. T=T₂.

Производительность заявленного способа шифрования сообщения M, представленного в виде МДЧ, примерно равна производительности его ближайшего аналога, поскольку вычислительная сложность как первого, так и второго способа примерно равна вычислительной сложности операции извлечения квадратного корня по простому модулю p и операции извлечения квадратного корня по простому модулю q. Для уменьшения вычислительной сложности операции извлечения квадратных корней по простым модулям p и q можно выбирать в качестве секретного ключа МДЧ p и q, которые удовлетворяют условиям p≡3 mod 4 и q≡3 mod 4 [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С.-Петербург. Петербург - БХВ, 2010. - 304 с.; см. с.25].

Таким образом, приведенные математические выкладки и конкретные примеры реализации показывают, что заявленный способ шифрования сообщения M, представленного в виде МДЧ, технически реализуем и позволяет достичь сформулированного технического результата.

Заявляемый способ шифрования сообщения M, представленного в виде МДЧ, может быть применен для разработки средств защиты информации, передаваемой по открытым телекоммуникационным каналам, от несанкционированного доступа.

Толкование терминов, используемых в описании изобретения

1. Двоичный цифровой электромагнитный сигнал - последовательность битов в виде нулей и единиц.

2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов.

3. Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например число 10011 является 5-разрядным.

4. Битовая строка - двоичный цифровой электромагнитный сигнал, представляемый в виде конечной последовательности цифр «0» и «1».

5. Секретный ключ - двоичный цифровой электромагнитный сигнал, используемый для формирования подписи к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1».

6. Открытый ключ - битовая строка, параметры которой зависят от секретного ключа. Открытый ключ вычисляется по секретному как значение функции, вычислимой в одну сторону, которая делает практически неосуществимым вычисление секретного ключа по открытому ключу.

7. Многоразрядное двоичное число (МДЧ) - двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1».

8. Разрядность МДЧ - это число двоичных разрядов (битов) в записи МДЧ по двоичному основанию.

9. Простое МДЧ - это МДЧ, которое делится только на единицу и на само себя.

10. Взаимно простые МДЧ - это МДЧ, наибольший общий делитель которых равен единице.

11. Сравнимость двух заданных значений по модулю некоторого числа m - это равенство остатков от деления заданных значений на m [Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. - 384 с.].

12. Сравнение - выражение, состоящее из правой и левой частей, такое, что значение левой части сравнимо со значением правой части по заданному модулю [Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. - 384 с.].

13. Обратный элемент по модулю n к числу a, являющемуся взаимно простым с n, есть натуральное число, обозначаемое как a^-1, для которого выполняется условие a^-1a=1; для любого числа, являющегося взаимно простым с модулем, существует элемент, обратный этому числу. Известны эффективные алгоритмы вычисления обратных элементов [Романец Ю.В., Тимофеев П.А., Шань-гин В.Ф. Защита информации в компьютерных системах и сетях. - М.: Радио и связь. - с.308-310].

14. Операция возведения числа S в дискретную степень A по модулю n - это операция, выполняемая над конечным множеством натуральных чисел {0, 1, 2, …, n-1}, включающем n чисел, являющихся остатками от деления всевозможных целых чисел на число n; результат выполнения операций сложения, вычитания и умножения по модулю n представляет собой число из этого же множества [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.];

операция возведения числа S в дискретную степень Z по модулю n определяется как Z-кратное последовательное умножение по модулю n числа S на себя, т.е. в результате этой операции также получается число W, которое меньше или равно числу n-1; даже для очень больших чисел S, Z и n существуют эффективные алгоритмы выполнения операции возведения в дискретную степень по модулю.

12. Сложность операции Oper - количество стандартных элементарных битовых операций (т.е. операций над битами), которые необходимо осуществить для выполнения операции Oper. Чем сложнее операция, тем больше время ее выполнения.

1. Способ шифрования сообщения, представленного в виде многоразрядного двоичного числа, заключающийся в том, что генерируют секретный ключ (p, q) в виде двух простых многоразрядных двоичных чисел p и q, генерируют открытый ключ в виде многоразрядного двоичного числа n=pq, формируют криптограмму C в зависимости от сообщения M и открытого ключа n и восстанавливают сообщение M из криптограммы C по секретному ключу (p, q), отличающийся тем, что дополнительно генерируют вспомогательное многоразрядное двоичное число R<n, криптограмму C формируют в виде пары (A, B) многоразрядных двоичных чисел A и B в зависимости от сообщения M, открытого ключа n и многоразрядного двоичного числа R, а восстанавливают сообщение M путем решения уравнения x²-Ax+B=0 mod n относительно неизвестного x и вычисления сообщения M из одного из решений указанного уравнения.

2. Способ по п.1, отличающийся тем, что криптограмму C формируют в виде пары (A, B) многоразрядных двоичных чисел A и B, генерируемых по формулам A=(R+n-M-1) mod n и B=R(n-M-1) mod n.

3. Способ по п.1, отличающийся тем, что криптограмму C формируют в виде пары (A, B) многоразрядных двоичных чисел A и B, генерируемых по формулам A=(2R-M) mod n и B=R(R-M) mod n.

4. Способ по п.1, отличающийся тем, что дополнительно генерируют вспомогательное многоразрядное двоичное число R<n путем генерации вспомогательного сообщения T и вычисления R по формуле R=(n-T)² mod n.