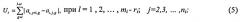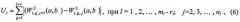Способ исследования электроэнцефалограммы человека и животных

Способ исследования электроэнцефалограммы человека и животных

Иллюстрации

Показать все

Реферат

Изобретение относится к медицине, а точнее к функциональной диагностике нормальной и патологической физиологии.

Известен способ изучения электроэнцефалограмм человека и животных (Патент №2332160 Зарегистрирован в Российском агентстве по патентам и товарным знакам 27 августа 2008 г.), основанный на регистрации ЭЭГ и дальнейшей ее спектральный анализ методом непрерывного вейвлет-преобразования, в котором определяют мощность частоты кардиоинтервалограммы a в момент времени b по формуле:

, a, b∈R, а>0,

где W(a,b) - коэффициент вейвлетного преобразования;

f (t) - анализируемая функция;

ψ((t-b)/a) - анализирующий вейвлет;

построение на основе матрицы вейвлетных коэффициентов скейлограмм на отрезке [b_i,b_j] по формуле:

, i, j<N, j>i,

где V(a _l) - скейлограмма сигнала;

N - количество коэффициентов;

a _l - масштаб вейвлетного преобразования;

выделение на скейлограммах физиологически значимых частотных диапазонов исходя из расстояний между соседними локальными минимумами на кривой скейлограммы по формуле:

где Δa - физиологически значимый диапазон, a _m, a _n - соседние локальные минимумы на кривой скейлограммы;

определение значения вейвлетной плотности мощности (ВПМ) U в каждом из частотных диапазонов по формуле:

,

определение изменения вейвлетной плотности мощности во времени как U(t);

определение изменения частотных диапазонов во времени как Δa(t);

определение значения удельной вейвлетной плотности мощности U' во времени по формуле:

U'=U(t)/Δa(t),

которая отражает динамику изменения активности различных генераторов ЭЭГ на коротких промежутках времени.

Скейлограммы («энергетические» диаграммы) строятся на основе матрицы вейвлет-коэффициентов, заданные как среднее квадратов коэффициентов W(a,b) при фиксированном параметре а на отрезке [b_i, b_j]. Являясь функцией масштаба, скейлограмма отражает ту же информацию, что и спектральная плотность мощности Фурье, являющаяся функцией от частоты. Как известно, вейвлет-преобразование имеет преимущество, прежде всего, за счет свойства частотно-временной локализации вейвлетов. Вейвлет-преобразование, представляющее собой временную развертку спектра, позволяет получить и более локализованную во времени энергетическую информацию. Энергетические диаграммы (скейлограммы) строятся на кратковременных (порядка 0,01 секунд при частоте дискретизации в 5000 Гц) отрезках, что позволяет отслеживать временную динамику процесса.

На скейлограммах выделяют локальные спектры и физиологически значимые частотные диапазоны Δa, которые рассчитывают исходя из расстояний между локальными минимумами a _m, a _n, связанными с различными типами механизмов регуляции В CP человека. При этом, при выявлении трех наиболее значимых диапазонов определяются два наиболее выраженных минимума, при четырех - три и т.д.

Суммарное значение вейвлетной плотности мощности U отражает суммарную активность нервного центра и определяется в каждом из частотных диапазонов .

Удельная вейвлетная плотность мощности U' характеризует удельную выраженность активного нервного центра и отражает процессы изменения во времени вклада нервных центров, генерирующих определенные частоты в общую картину ЭЭГ. Выделение физиологически значимых диапазонов между локальными минимумами на кривой скейлограммы, связанных с различными ЭЭГ ритмами, оценка данного параметра позволяют выявить даже малые по амплитуде ритмические активности на различных этапах онтогенеза, в норме и патологии, как в покое, так и при переходных процессах, что качественным образом повышает информативность и точность способа оценки ЭЭГ. Введение временной оценки удельной вейвлетной плотности мощности позволяет описать динамику изменения активности генераторов различных ритмов ЭЭГ в покое на коротких промежутках времени.

К недостаткам данного метода следует отнести непрерывность оценки структуры локальных минимумов, таким образом, что возникающие в частотном пространстве «разрывы» искусственно объединяются. Действительно, исходя из фиг.1 видно, что структуры локальных минимумов (светло-серые линии на фоне темно-серой заливки) в ряде случаев искусственно соединены другими структурами через области локальных максимумов (светло-серая заливка). Иными словами, отсутствуют критерии, по которым можно определить появление цепочки локальных минимумов, присоединение к этой цепочке последовательности из нескольких локальных минимумов и, следовательно, рассчитанные частотные диапазоны не всегда являются корректными.

Известна программа PikWave (регистрационный №2006613500), обеспечивающая анализ как локальных минимумов, так и локальных максимумов, на скейлограмме по формуле (2), построенной на матрице W(a,b). Программа реализует расчеты и построение их цепочек локальных максимумов и минимумов и расчет значений вейвлетной плотности мощности в динамически изменяющихся диапазонах. К недостаткам этой программы следуете отнести, как и в случае патента, как наличие искусственных соединений цепочек локальный минимумов, так и аналогичный алгоритм для цепочек локальных максимумов. Уточним, что аббревиатура ЦЛМ будет обозначать цепочки локальных максимумов, а цепочки локальных минимумов - ЦЛМин, если не оговорено иное. Тем не менее, настройки этой программы позволяют получать значения цепочек локальных максимумов и минимумов как в виде их истинных координат на матрице вейвлет-коэффициентов, так и в виде их координат в частотно-временной плоскости, сглаженной методом скользящего среднего. При этом будут наблюдаться различия между расчетными и истинным положением экстремумов локального вейвлетного спектра.

Известна также статья «Возрастные изменения частотно-временной структуры сонных веретен на ЭЭГ у крыс с генетической предрасположенностью к абсанс-эпилепсии (линия wag/rij)» Е.Ю. Ситникова, В.В. Грубов, А.Е. Храмов, А.А. Короновский, Журнал высшей нервной деятельности. 20/2, том 62. №6, с.733-744. В статье отсутствует упоминание о локальных минимумах, а в случае с локальными максимумами очевидной ошибкой является отсутствие правил, по которым определяется начало и конец цепочки, которую они формируют. Действительно, как видно на рисунке 1 данной статьи, в расчет включены (и даже отражены на графике) не все цепочки, а только то, что по своей координате времени входит в зону сонных веретен. При этом повторимся: остальные цепочки даже не визуализированы. Таким образом, возможны ситуации, когда имеющаяся ЦЛМ, которую анализируют авторы, представляет собой продолжение значительно ранее начавшейся ЦЛМ. Аналогичная ситуации и с прекращением ЦЛМ. Очевидно, что отсутствие не только правил, по которым осуществляется прерывание ЦЛМ, но и даже примитивной визуализации всех ЦЛМ данной матрицы квадратов вейвлет-коэффициентов делает невозможной оценку корректности их построения. Очевидно, авторы и не задумывались над данными правилами, иначе они были бы приведены. Помимо этого в статье учитывается средняя частота и начальные и конечны частоты ЦЛМ. Поскольку отсутствуют алгоритмы определения начала и конца ЦЛМ, т.е. критерии, по которым локальный максимум считается началом точки, и критерии, по которым он считается ее концом, то содержательная часть в оценке частот локальных максимумов, выделенных подобным образом, стремится к нулю. Нельзя не отметить, что крайне скупо в статье присутствует упоминание о различных типах ЦЛМ. Основу для их классификации, по мнению авторов, составляет только частота ЦЛМ, при этом не учитывается форма ЦЛМ. Однако не проведено исследование распределения ЦЛМ по форме. Действительно, исходя из рисунка 2 означенной статьи, видно, что в ряде случаев распределение типов изучается только по одной частоте, а разделение на типы - не по минимумам гистограммы, а захватывает более высокие значения, что не позволяет оценить эту классификацию как проведенную корректно.

Известна также программа Wavemax 1.0 №2012614720. Программа в отличие от приведенной выше статьи позволяет осуществлять выделение ЦЛМ исходя из правил, которые задает пользователь. Критериями включения локального максимума или минимума в ЦЛМаксимумов или ЦЛМинимумов служит расстояние в частотном и временном пространстве, которое может задаваться как в виде константы, так и в виде динамического показателя. Однако в программе отсутствуют алгоритмы расчета данных значений, что требует при ее использовании достаточно квалифицированного пользователя. При этом программа является по сути лишь инструментом и не содержит физиологической интерпретации полученных данных.

Задачей предлагаемого изобретения является улучшение оценки электроэнцефалограммы человека и животных в различных функциональных состояниях.

Технический результат заключается в увеличении точности и информативности способа исследования ЭЭГ человека и животных в различных функциональных состояниях.

Технический результат достигается тем, что способ исследования электроэнцефалограммы человека и животных включает регистрацию ЭЭГ и дальнейший ее спектральный анализ методом непрерывного вейвлет-преобразования, в котором определяют мощность частоты а электроэнцефалограммы в момент времени b по формуле:

, a, b∈R, а>0,

где W(a,b) - коэффициент вейвлетного преобразования;

f (t) - анализируемая функция;

ψ((t-b)/a) - анализирующий вейвлет.

На основе матрицы вейвлет-коэффициентов W(a,b) можно построить «энергетические» диаграммы - скейлограммы V(a _l) сигналов как среднее значение квадратов этих коэффициентов при фиксированном параметре масштаба a _l:

где N - число усредняемых вейвлет-коэффициентов W(a _l,b_k)

На фиг.2 дан график зависимости величины вейвлетной плотности мощности W (a, b) от масштаба a вейвлет-преобразования для пациента в состоянии покоя. Зависимость величины вейвлетной плотности мощности W²(a, b) от масштаба а вейвлет-преобразования для пациента в состоянии покоя. Использовано отведение Oz, частота дискретизации сигнала - 1кГц, время построения скейлограммы - 10 мс с шагом 20 мс. Спектры построены в следующем порядке: сплошная линия, пунктирная, точечная и штрихпунктирная. По сути сигнал представляет набор скейлограмм, V(a _l).

Можно заметить из фиг.2, что разные локальные спектры ЭЭГ имеют различное расположение экстремумов в частотном пространстве, что с физиологической точки зрения характеризует изменение периода колебаний исследуемых параметров, выделенных пользователем. Таким образом, получив в результате расчетов количество локальных максимумов на одной скейлограмме (т.е. на локальном спектре), можно оценить число осцилляторов, участвующих в формировании сигнала ЭЭГ в конкретном отведении (по сути, имеющихся в данной области головного мозга) и определить частоту их колебаний.

В большинстве опубликованных в настоящее время работ значения экстремумов W²(a, b) вычисляются при постоянном масштабе а вейвлет-преобразования, что дает, например, возможность рассчитать параметр d, который трактуется Н.М. Астафьевой как "фрактальная размерность исследуемого ряда". Однако если проводить расчеты не при постоянном значении масштаба a, а при постоянном времени (b), то распределение локальных максимумов и минимумов частотного спектра будет изменяться. Очевидно, что в общем случае координаты локальных максимумов и минимумов W²(a, b) в пространстве (a,b) не будут совпадать друг с другом.

В первую очередь, речь идет о том, что использование разных типов вейвлетов приводит к разному разрешению по частоте исследуемых сигналов. Из соотношения (3) следует, что при использовании одного из самых популярных видов вейвлетов для анализа биомедицинских данных - вейвлета Морле - можно с разрешением менее 1 Гц достаточно подробно исследовать сигнал ЭЭГ при частоте его дискретизации 1 кГц, начиная с частоты в 32 Гц, что охватывает большую часть частот ЭЭГ. Но это не дает возможности во всей полноте проанализировать малоисследованные высокие частоты γ-ритма, диапазон которых - от 35 Гц и выше. Наряду с этим такое разрешение по частоте можно применять только при компьютерном offline-исследовании, поскольку при использовании вейвлетов Морле невозможно проводить оперативный вейвлет-анализ ЭЭГ с задержкой менее 2-3 с, что, например, является проблемой при использовании таких вейвлетов в технологиях нейрокомпьютерного интерфейса или биологической обратной связи.

Отсюда возникает необходимость применения, обеспечивающего лучшую локализацию во временном пространстве типов вейвлетов, однако при этом произойдет ухудшение частотного разрешения сигнала. Так применение вейвлета типа WAVE позволяет выйти на обозначенный уровень разрешения, полученный с использованием вейвлета Морле, только для частот <13 Гц, вейвлета МНАТ - <15 Гц, вейвлета DOG-8 - <20 Гц. Иными словами, волны электромагнитных колебаний нейронного ансамбля, частоты которых находятся в диапазоне наилучшего выделения их конкретными вейвлетами, могут значительно уменьшить свои амплитуды. Следовательно, они могут остаться недетектированными указанными выше способами или же будут отнесены к одной из центральных частот, на которых происходит вейвлет-анализ, что исказит результаты исследования.

Рассмотрим теперь ход изменения положения локальных максимумов вейвлетной плотности мощности W²(a, b), отмечаемого в процессе анализа регистрируемого сигнала ЭЭГ.

На фиг.3,4, где в координатах масштаб - время представлены картины расположения локальных максимумов вейвлетной плотности мощности W²(a, b) при использовании отведения Oz, частоты дискретизации сигнала - 1кГц и периода построения скейлограммы - 1 мс, видна характерная древовидная структура этой зависимости. При этом для фиг.3 локальные максимумы строились при фиксированном времени, а для фиг.4 - при фиксированной частоте (масштабе).

На фиг.5 (использовано отведение Oz, частота дискретизации сигнала - 1кГц, период построения скейлограммы - 1 мс) представлен пример динамической картины поведения локальных максимумов вейвлетной плотности мощности W²(a, b) для ЭЭГ в состоянии покоя пациента. Как видно из фигуры, можно выделить два типа динамических картин частот ЭЭГ: "активирующая" (область Б, характеризующаяся повышением частоты и появлением новых частотных пиков на скейлограммах) и "угасающая" (область А, характеризующаяся снижением частоты выбранного осциллятора и уменьшением числа осцилляторов, участвующих в формировании сигнала ЭЭГ). Интерпретация результатов динамических картин поведения локальных максимумов вейвлетной плотности мощности W²(a, b) позволяет выявить изменение активности нейронных ансамблей, формирующих сигнал ЭЭГ. Увеличение частоты выбранного осциллятора и появление новых осцилляторов (или рассогласование работы уже существующих ансамблей) характерно, например, для ориентировочной реакции, а синхронизация их работы и снижение частот - для состояния сна.

Рассмотрим выделенный блок А на фиг.5. Хорошо видно, что в течение определенного времени (~ 20-50 мс) период колебаний волны ЭЭГ в ряде случаев остается почти постоянным, то есть масштаб а вейвлет-преобразования, соответствующий пиковой частоте в данном частотном диапазоне ЭЭГ, лишь незначительно дрейфует в область увеличения периода данной волны. В дальнейшем следует резкий переход (скачок) частоты исследуемой волны ЭЭГ на уровень более низких частот. Так происходит несколько раз до тех пор, пока осциллятор, продуцирующий данные частоты, не исчезнет.

Использование различных вариантов кластерного анализа позволило подтвердить, что отмеченные точки на фиг.5 действительно лежат ближе друг к другу, чем точки, отмечающие локальные максимумы, входящие в иные последовательности локальных максимумов на матрице W²(a, b), что позволяет интерпретировать их именно в качестве одного или группы тесно связанных между собой осцилляторов, а не в виде отдельных независимых нейронных ансамблей. Здесь важно отметить, что процесс изменения и скачков частот ритмов ЭЭГ захватывает одновременно и диапазон β-ритма, и высокочастотный поддиапазон α-ритма без их разделения, однако такое разделение традиционно проводится при проведении исследований непосредственно по медицинской тематике.

На блоке Б фиг.5 представлен процесс, обратный по отношению к процессу, отмеченному в блоке А. Хорошо видно, что в том же частотном диапазоне (а именно при изменении частот от ≈ 9 Гц до ≈ 35 Гц) происходит дрейф пиковой частоты выявленных осцилляторов в область высокочастотного β-ритма. Но при этом исчезновение одного пика, то есть прекращение работы на близких частотах группы нервных клеток приводит к появлению двух пиков, природа которых в настоящее время неизвестна. Первый находится в интервале более высоких частот и, как правило, в области, принадлежащей доверительному интервалу точек линии регрессии, построенной на основе координат локальных максимумов предыдущего осциллятора. Второй находится в том же частотном диапазоне, что и предыдущий пик, и во многом повторяет его динамику: зарождается на более низких частотах, дрейфует в сторону высокочастотных диапазонов и в дальнейшем через некоторое время исчезает. Вопрос о том, какой из вновь появившихся осцилляторов является физиологическим (морфо-функциональным) "преемником" осциллятора, уже прекратившего свою работу, требует более детальных биомедицинских исследований.

Особое внимание следует обратить на анализ γ-ритма. Можно заметить, что описанные выше изменения частотных координат пиков осцилляторов наблюдаются гораздо реже в диапазоне частот γ-ритма по сравнению с более низкочастотными диапазонами, что объясняется значительно худшим разрешением использованного вейвлета по частоте на более высоких частотах. Тем не менее, наличие дрейфа частот как в сторону их уменьшения, так и в сторону увеличения показывает, что частоты пиков γ-ритм, связываемые с корковой активностью мозга и когнитивными функциями, изменяются значительно сильнее, чем для α- и β-ритмов. Так, для γ-ритма изменение пиковой частоты ЭЭГ в течение 1-2 мс составляет величину ≈ 5-15 Гц, тем временем как в более низкочастотных диапазонах такие изменения не превышают ≈ 2-5 Гц.

Формализуем правила определения локальных максимумов и минимумов. Ключевым моментом в формировании такой цепочки или же в ее прерывании являются правила, по которым новая координатная точка (a, b), соответствующая локальному максимуму/минимуму на скейлограмме, включается или не включается в уже имеющуюся ЦЛМ.

Для определения того, как формируются ЦЛМ, то есть, по сути, для получения картины кластеризации локальных максимумов/минимумов был создан и апробирован ряд алгоритмов, использующих величины масштаба и времени вейвлет-преобразования, изменяющиеся с постоянным шагом, или осуществляющих динамическую, то есть зависящую от масштаба генерацию этих параметров.

На фиг.6 (цепочки локальных максимумов определяются по динамическим правилам (круглые черные маркеры), при фиксированном значении масштаба (ромбовидные черные маркеры) и времени (квадратные светлые маркеры) представлена зависимость между величинами a и отношением Δt/k (разности времени окончания и начала ЦЛМ или ЦЛМин в случае построения цепочек минимумов к числу входящих в нее точек) для вейвлета Морле, полученная при использовании оптимального алгоритма для принятия решения о включении в ЦЛМ или ЦЛМин конкретной точки, характеризующей частотно-временное расположение локального максимума. Как видно из фиг.6, при динамическом формировании условий для включения точки в ЦЛМ (круглые черные маркеры) или ЦЛМин исследуемое отношение с увеличением масштаба вейвлет-преобразования (уменьшением частоты) быстро приближается к единице, что отражает отсутствие в ЦЛМ «выпадающих точек». Подобные точки возникают в том случае, когда происходит объединение двух разных ЦЛМ или ЦЛМин, между которыми отсутствуют локальные максимумы/минимумы, расположенные в окрестности данного значения масштаба временных отсчетов. Фиксированные значения окрестностей концевой точки ЦЛМ, в которых должна находиться следующая точка ЦЛМ, представлены квадратными прозрачными маркерами (область масштабов вейвлет-преобразования ±10 значений в случае, если масштаб a конечной точки ЦЛМ был меньше 10, то диапазон масштабов вейвлет-преобразования рассматривался от 0 до a+10, область по времени: +10 значений) и ромбовидными черными маркерами (область масштабов вейвлет-преобразования ±50 значений, область по времени +50 значений). Видно из фиг.6, что если в первом случае зависимость только несколько уступает зависимости, полученной на основе динамически формируемого правила включения локальных максимумов в ЦЛМ, что представляется несколько большими масштабами a, на которых отношение Δt/k достигает максимальных значений, то во втором случае ЦЛМ представляют собой неверно объединенные локальные максимумы, то есть ЦЛМ, разделенные «пустыми» участками, не содержащими в исследуемые моменты времени локальных максимумов, что хорошо видно по низким значениям отношения Δt/k. Важно отметить, что аналогичные зависимости были получены и для локальных минимумов.

В ходе анализа 64-х ЭЭГ, зарегистрированных по 21-му каналу с частотой дискретизации 1 kHz на канал как в состоянии покоя, так и при фотостимуляции, при решении человеком образных и логических задач, а также при его работе с нейрокомпьютерными интерфейсами, реализованными по технологиям SSVEP и Р300, было получено правило максимизации отношения Δt/k. Суть этого правила в том, что оно дает возможность, с одной стороны, выделить ЦЛМ или ЦЛМин, а с другой - избежать чрезмерного объединения таких ЦЛМ или ЦЛМин, при котором между ними наблюдаются частотно-временные области без локальных максимумов/минимумов. Используя это правило, получено выражение для логической функции f(a, b) принятия решения о включении (или невключении) локального экстремума с координатами (a _i, b_i) в конкретную ЦЛМ или ЦЛМин:

где a _i-1 - масштаб локального максимума/минимума концевой точки ЦЛМ или ЦЛМин, ближайшей по величине масштаба к предполагаемому для включения в ЦЛМ или ЦЛМин локальному максимуму/минимуму; b_j-1 - время (или номер отсчета, номер скейлограммы) концевой точки ЦЛМ или ЦЛМин, ближайшей по времени (номеру отсчета, номеру скейлограммы) к аналогичному значению предполагаемого для включения в ЦЛМ или ЦЛМин локального максимума/минимума; a _s - значение масштаба первой точки формирующейся ЦЛМ или ЦЛМин. Константы u и ν получены при использовании правила максимизации отношения Δt/k и при наибольших для данного диапазона масштабов значений k. Для вейвлетов Морле и WAVE u=3 и ν=0,05.

Полученное таким образом множество ЦЛМ или ЦЛМин может быть подвергнуто дальнейшей обработке с целью выявления в них значимых элементов. Целесообразно использовать для этого следующие характеристики ЦЛМ или ЦЛМин: масштаб вейвлет-преобразования a (или соответствующая частота), при котором появилась (a _s) или прервалась (a _f), данная ЦЛМ или ЦЛМин; время появления t_s и прекращения t_f ЦЛМ или ЦЛМин; длительность ЦЛМ или ЦЛМин Δt=t_f-t_s; «дрейф» масштаба Δa=a _s-a_f; количество k локальных максимумов/минимумов в ЦЛМ или ЦЛМин; отношение Δt/k, отражающее «плотность» локальных максимумов/минимумов в ЦЛМ или ЦЛМин.

Рассмотрим результаты дальнейшего анализа полученных ЦЛМ или ЦЛМин.

В основу метода положена парадигма, основанная на использовании идеологии выделения вызванных потенциалов (ВП) головного мозга. Как известно, ВП представляют собой низкоамплитудные колебания электрического поля мозга, возникающие в ответ на определенные стимулы (вспышку света, резкий звук, щелчок, тактильное раздражение и т.п.) или предшествующие определенным действиям (например, сокращению мышц). Поскольку амплитуда ВП значительно ниже амплитуд колебаний для фоновой ЭЭГ, в предлагаемом методе для улучшения отношения сигнал/шум используется когерентное накопление фрагментов ЭЭГ, связанных с изучаемым стимулом, что позволяет провести детальный анализ ВП.

В ходе исследования проводится усреднение в частотно-временном пространстве частот локальных максимумов, присутствующих в данной ЦЛМ или ЦЛМин, для получения C_i,k - значений координат усредненной ЦЛМ или ЦЛМин i-го типа:

где a _i,j,k - значение частоты локального максимума; i=1, …, 5 - тип ЦЛМ или ЦЛМин; j=1, …, n_i - номер цепочки в массиве ЦЛМ или ЦЛМин данного типа i (номера цепочек устанавливаются в соответствии с их длиной, меньший номер соответствует большей длине, общее количество цепочек типа i равно n_i); k=1, …, m_i - номер точки в конкретной ЦЛМ или ЦЛМин типа i; m_i - количество точек в наиболее длинной ЦЛМ или ЦЛМин i-го типа.

Важным моментом при использовании данного метода является выбор начальной точки для усреднения ЦЛМ или ЦЛМин как в частотном, так и во временном пространстве.

Для решения этой задачи во временном пространстве было использовано два подхода.

В первом из них усреднение выполняется после совмещения первых точек ЦЛМ или ЦЛМин, так что времена появления первых локальных максимумов t_s1, t_s2, …, t_sn будут равны нулю, где t_s1 - время (или номер отсчета) появления первого локального максимума первой ЦЛМ или ЦЛМин; t_s2 - время (или номер отсчета) появления первого локального максимума второй ЦЛМ или ЦЛМин при его наличии; t_sn - время (или номер отсчета) появления локального максимума вейвлет-спектра, формирующего первую точку n-й цепочки, используемой в расчетах. Затем проводится синхронизация всех координат ЦЛМ или ЦЛМин во временном пространстве, заключающаяся в том, что рассчитываются средние значения частот для усредненной ЦЛМ или ЦЛМин. В случае если в одной из ЦЛМ или ЦЛМин отсутствует точка с определенными временными координатами (на фиг.7 этот случай указан стрелкой), то в общей суммации для данной временной координаты такая ЦЛМ или ЦЛМин не участвует. Следовательно, здесь усреднение осуществляется только по точкам, полученным в ходе расчета ЦЛМ или ЦЛМин, без учета «искусственно» построенных точек, например, в результате аппроксимации или интерполяции, которые могут заполнять участки ЦЛМ или ЦЛМин без локальных максимумов.

Во втором подходе используется функция U_i, характеризующая степень различия цепочек в частотном пространстве:

r_i - число точек в текущей ЦЛМ или ЦЛМин i-го типа. Остальные обозначения те же, что и в формуле (4).

Требуется найти целое l, при котором значение функции U_i будет наименьшим. Минимум функции U_i будет указывать на такое взаиморасположение ЦЛМ или ЦЛМин во временном пространстве, при котором их различие в частотном пространстве будут минимальными. Т.о. для получения итоговой усредненной ЦЛМ или ЦЛМин перед процессом усреднения каждая цепочка для j>1 сдвигается во временном пространстве на l_j, где l_j - значение l, соответствующее минимальному U_i для цепочки i-го типа с номером j.

Нетрудно заметить, что использование данного подхода, в котором ЦЛМ или ЦЛМин перед последующим усреднением выстраиваются, перемещаясь во временном пространстве путем изменения всех временных координат ЦЛМ за счет прибавления к ним константы l, позволяет минимизировать в частотном пространстве отличия данной ЦЛМ или ЦЛМин от ЦЛМ или ЦЛМин с максимальным числом локальных максимумов/минимумов. При этом следует обратить внимание, что минимизация этих различий осуществляется именно с использованием шкалы значений, измеряемых в Гц, а не в масштабах вейвлет-преобразования, так как в этом случае данные, полученные для разных вейвлетов для одного и того же сигнала, могут существенно различаться. К тому же, используя именно частотное пространство и зная разрешение различных вейвлетов для определенных масштабов вейвлет-преобразования исследуемого сигнала, можно наиболее корректно интерпретировать классифицированные данные.

Реализация данных способов усреднения ЦЛМ или ЦЛМин в изложенном выше виде сталкивается, однако, с рядом проблем. В частности, длина ЦЛМ или ЦЛМин как во временном пространстве, так и характеризуемая числом точек, зависит от частоты (масштаба вейвлет-преобразования). Таким образом, суммация двух ЦЛМ или ЦЛМин, появившихся на ЭЭГ на частотах, например 3 и 35 Гц, представляется бессмысленной не только с физиологической точки зрения, но и с точки зрения численной обработки исследуемого сигнала. Для устранения данной проблемы применялось разделение на поддиапазоны всего исследуемого диапазона частот ЭЭГ: нижняя граница исследуемого поддиапазона бралась равной нижней границе θ-ритма, а верхняя - частоте Найквиста для данного электроэнцефалографа. Можно пользоваться таким разделением как в рамках «классического» варианта анализа ЭЭГ, так и путем построения поддиапазонов, исходя из динамических характеристик их границ, основанном на частотных значениях локальных минимумов, которые подобно максимумам ЦЛМ или минимумам ЦЛМин также изменяют свои частотные характеристики.

Другая проблема, возникающая при получении усредненных ЦЛМ или ЦЛМин методом когерентного накопления, связана с их весьма различающейся динамикой поведения во времени.

Как видно из фиг.7 (распределение локальных максимумов в матрице квадратов коэффициентов вейвлет-преобразования W²(a, b) сигналов ЭЭГ, построенное на основе скейлограмм; отведение Oz, частота дискретизации сигнала - 1 кГц; по горизонтальной оси отложено время в мс, по вертикальной оси - масштаб вейвлет-преобразования; стрелкой указано наличие «разрыва» в ЦЛМ; области: А - ЦЛМ первого; Б - второго; В - третьего; Г - четвертого; Д - пятого типа), можно выделить пять различных типов характера поведения ЦЛМ или ЦЛМин:

1) ЦЛМ или ЦЛМин со стабильно нарастающей частотой (фиг.7, область А). Такие ЦЛМ или ЦЛМин во многом свойственны ЭЭГ в состоянии покоя. Характер увеличения частоты локального максимума/минимума для разных случаев здесь различен, что, возможно, позволит выделить несколько подтипов данного типа поведения ЦЛМ или ЦЛМин. Поведение ЦЛМ или ЦЛМин в частотном пространстве различается как по скорости ν дрейфа частот (ν=ω/t, где - ω частота; t - время; v измеряется в Гц/с), так и по форме получившейся ЦЛМ в пространстве время - масштаб вейвлет-преобразования. Наблюдаются следующие виды динамики поведения ЦЛМ или ЦЛМин: а) линейно-равномерная (когда зависимость ν(t) хорошо аппроксимируется линейной функцией); б) неравномерная (когда тренды, построенные по началу и концу ЦЛМ или ЦЛМин, отличаются от ее центральной части).

2) ЦЛМ или ЦЛМин со стабильно убывающей частотой (фиг.7, область Б). Так же, как и для ЦЛМ или ЦЛМин первого типа, характер снижения частоты для ЦЛМ данного типа достаточно сильно различается. Возможно, «стабильно убывающий тип» представляет собой обратный по сравнению с типом 1 вариант функционирования осцилляторов, модулирующих электрическую активность головного мозга, порождающих поведение ЦЛМ или ЦЛМин первого типа.

3) ЦЛМ или ЦЛМин без динамики изменения в частотном пространстве (фиг.7, область В). Осциллятор (или группа осцилляторов) головного мозга не увеличивает и не уменьшает свою частоту в пределах разрешающей способности используемого вейвлета.

4) ЦЛМ или ЦЛМин, в которых сначала происходит рост частоты, а потом ее уменьшение, притом, что ЦЛМ или ЦЛМин может завершиться как на более высокой, так и на более низкой по сравнению с начальной частоте (фиг.7, область Г).

5) ЦЛМ или ЦЛМин, демонстрирующие первоначальное уменьшение частоты с последующим ее ростом. Как и для ЦЛМ или ЦЛМин предыдущего типа, отношение частот начала и завершения ЦЛМ или ЦЛМин может быть различным (фиг.7, область Д).

Проведенная выше типологизация локальных максимумов/минимумов матриц вейвлет-коэффициентов для ЭЭГ имеет важное значение для исследования процессов ЭЭГ в различных функциональных состояниях человека.

Продемонстрируем теперь возможности метода применительно не к частотной, а к энергетической составляющей ЦЛМ или ЦЛМин.

Для корректного усреднения амплитудных параметров ЦЛМ или ЦЛМин предлагается три подхода, использующие различные критерии выбора точек пространства (W²(a, b)) для синхронизации ЦЛМ (фиг.8 - схематическое изображение трех подходов к взаиморасположению ЦЛМ по оси b (время, номер локального спектра) при вычислении усредненных данных по энергии ЦЛМ; по оси OX отложена величина b, отражающая время процесса, по оси OY - значения W²(a, b), характеризующие энергию процесса, происходящего в заданном диапазоне частот ЭЭГ; А - усреднение при синхронизации по первому значению ЦЛМ; Б - усреднение при синхронизации при минимизации разницы по показателю W²(a, b); В - усреднение при синхронизация по показателям для двух ЦЛМ).

В первом подходе (см. фиг.8А) опорной точкой для проведения усреднения служит первое по времени значение в ЦЛМ или ЦЛМин, при этом остальные значения W²(a, b) в ЦЛМ или ЦЛМин выстраиваются по координате b таким образом, чтобы их порядковые номера отсчетов в различных ЦЛМ или ЦЛМин совпадали, и только после этого осуществляется усреднение. Данный подход аналогичен применяемому нами подходу к усреднению ЦЛМ или ЦЛМин по параметру масштаба (частоты) вейвлет-преобразования.

Второй подход (фиг.8Б) основан на минимизации различий ЦЛМ или ЦЛМин по значениям W²(a, b) в ЦЛМ или ЦЛМин. При этом одна ЦЛМ сдвигается относительно другой вдоль оси b до тех пор, пока между ними не установится минимальное различие между энергиями двух ЦЛМ или ЦЛМин:

где W²(a, b) - локальная энергия сигнала в момент времени b на частоте a; r_i - число точек в текущей ЦЛМ i-го типа; i=1, …, 5 - тип ЦЛМ или ЦЛМин; j=1, …, n_i - номер цепочки в массиве ЦЛМ или ЦЛМин данного типа i (номера цепочек устанавливаются в соответствии с их длиной, меньший номер соответствует большей длине, общее количество цепочек типа i равно n_i); k=1, …, m_i - номер точки в конкретной ЦЛМ или ЦЛМин типа i; m_i - количество точек в наиболее длинной ЦЛМ или ЦЛМин i-го типа.

Второй подход, так же как и первый, концептуально идентичен применяемому в наших исследованиях при оценке динамики ЦЛМ или ЦЛМин в частотном пространстве. В этом случае для характеристики W²(a, b) используются координаты а локальных максимумов ЦЛМ или ЦЛМин.

Третий подход (фиг.8В) основан на представлении о величинах W²(a, b) как о демонстрирующих энергию и в конечном счете амплитуду сигнала на заданной частоте, являющейся частотой локального максимума. Это позволяет предложить еще одно правило усреднения: ЦЛМ или ЦЛМин синхронизируются таким образом, чтобы различия и были минимальными, где - максимальная энергия первой ЦЛМ или ЦЛМин типа i, а максимальная энергия второй ЦЛМ или ЦЛМин типа i.

Очевидно, что при внешней схожести второй и третий подходы принципиально различаются. Второй подход минимизирует разницу между энергиями двух ЦЛМ или ЦЛМин в течение всего периода их существования. Таким образом, ищется такое взаимное распол