Способ определения напряженно-деформированного состояния материала с хрупким скелетом

Способ определения напряженно-деформированного состояния материала с хрупким скелетом

Иллюстрации

Показать все

Реферат

Изобретение относится к испытательной технике, в частности к области инженерных изысканий, и может быть использовано для определения напряженно-деформированного состояния пород, а именно определения стадии развития деформационных процессов в массиве материала (в горном массиве, грунтов под инженерным сооружением и т.п.).

Физико-механические параметры породы, как правило, определяют в лабораторных условиях. Механическая нагрузка вызывает в горных породах или грунте напряжения и деформации. На величину показателей физико-механических свойств материала влияют: анизотропия среды, силы и характер связей между частицами, размер включений, пористость, минеральный состав и т.п. Механические свойства подразделяют на упругие (модуль Юнга, коэффициент Пуассона и др.), прочностные (пределы прочности при сжатии, растяжении и др.), реологические свойства (период релаксации, предел длительной прочности, а также такие, как объемный модуль скелета породы (при учете порового давления) и пр. Для описания состояния породы используется ряд моделей с параметрами, которые определяются в результате испытаний материала. Например, для характеристики хрупкого скелета породы (гранит, гранулы песка с другими включениями и т.п.), а также энергетического состояния породы (трещиноватость и ее развитие под нагрузкой) в последнее время предложены коэффициенты α_±, α_J, α p ± , γ^± [1]. Постоянные коэффициенты α_±, α_J, α p ± характеризуют изменение потенциальной энергии упругого деформирования при рассеянном разрушении вследствие объемной деформации, сдвига и наличия порового давления. Причем коэффициенты α_J, α₊ , α p + > 0 , а α_-, α p − < 0 . Знак плюс в индексе ± соответствует рассеянному разрушению вследствие деформации растяжения, минус соответствует разрушению при сжатии. Положительные параметры γ^± - задают квадратичную зависимость поверхностной энергии ансамбля микротрещин в хрупком материале от накопленной трещиноватости, которая может интерпретироваться как предвестник разрушения материала ω.

Например, связь проницаемости с трещиноватостью можно определить при измерении проницаемости в процессе активного нагружения. Тензор полных напряжений и изменение пористости, определяемые упругой энергией деформируемого скелета, имеют в вид,

σ = ρ S 0 ∂ Ψ ( e , Δ p , ω ) ∂ e = ( K I 1 − b Δ p − α ± ω ) I + ( 2 μ − α J ω J ) e ' ,                      ( 1 ) ,

где σ=σ_S+σ_f - тензор полных напряжений, σ_S - тензор парциальных напряжений в скелете, σ_f - тензор парциальных напряжений во флюиде, Ψ - упругая энергия скелета, e - тензор малых деформаций, Δp - изменение внутрипорового давления, ρ S 0 - средняя плотность скелета в начальном состоянии, K - модуль сжимаемости скелета, µ - модуль сдвига, J - интенсивность касательных деформаций, e′ - девиатор тензора малых деформаций, I - единичный тензор второго ранга.

φ = − ρ S 0 ∂ Ψ ( e , Δ p , ω ) ∂ p = φ 0 + b I 1 + 1 N Δ p + α p ± ω                       ( 2 ) ,

где ϕ - пористость, ϕ₀ - пористость в начальном состоянии, I₁ - относительное изменение объема материала (I₁>0 - растяжение, I₁<0 - сжатие), N - модуль Био.

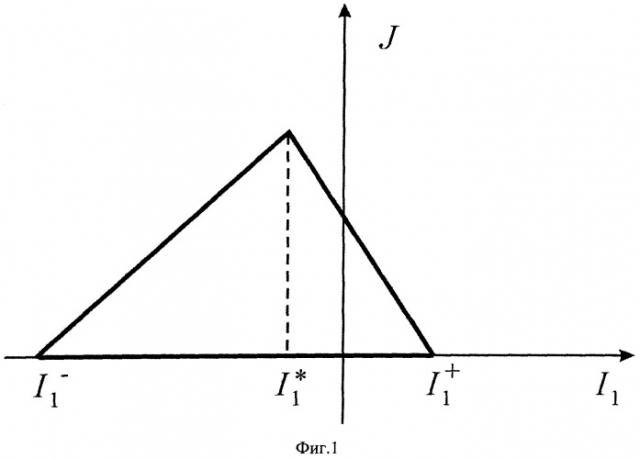
Процесс деформирования при нагружении породы, сопровождающийся развитием микротрещин, называют активным. Если развитие трещиноватости не происходит, то процесс называется пассивным. Область пассивного и активного процессов разделяет граница зоны упругости на полуплоскости I₁, J≥0 (фиг.1), уравнение которой

J = − α ± α J I 1 + γ ± − α p ± Δ p α J                                 ( 3 )

На полуплоскости (I₁, J≥0) функция (3) определяет зависящую от порового давления треугольную область (фиг.1). Из рисунка видно, что граница области упругости обладает сильной асимметрией относительно оси J, что связано с существенным различием прочностных свойств хрупкого скелета при растяжении и сжатии.

Уравнение границы упругой области имеет вид

J ( I 1 , Δ p ) = { J 0 ( 1 − I 1 / I 1 + ) , I 1 ∗ ≤ I 1 ≤ I 1 + J 1 ( 1 − I 1 / I 1 − ) , I 1 − ≤ I 1 ≤ I 1 ∗ ,                 ( 4 )

где J₀ - пороговое значение чистого сдвига (I₁=0), при превышении которого начинается разрушение, I 1 ± - значения объемной деформации, при которых начинается процесс роста поврежденности, а величина J 1 = J 0 ( 1 − I 1 ∗ / I 1 + ) / ( 1 − I 1 ∗ / I 1 − ) .

Связь величин, входящих в уравнение (4), с параметрами материала находится как:

J 0 ( γ − − α p − Δ p ) / α J ,    J 1 ( γ − − α p − Δ p ) / α J ,    I 1 + = ( γ + − α p + Δ p ) / α + , I 1 − ( γ − − α p − Δ p ) / α − ,    I 1 ∗ [ γ + − γ − − ( α p + − α p − ) Δ p ] / ( α + − α − ) .                   ( 5 )

Для медленных процессов, в которых уровень трещиноватости определяется текущей деформацией и поровым давлением, равновесное накопление трещиноватости (предвестника разрушения материала) ω определяется, как

ω = α ± I 1 + α J J + α p ± Δ p − γ ±                  ( 6 )

Соотношение (6) выполняется при условии активного нагружения ω≥0, ω ˙ > 0 , что дает α ± I 1 + α J J + α p ± Δ p > γ ± , α ± I ˙ 1 + α J J ˙ + α p ± Δ p ˙ > 0 .

В противном случае скорость изменения трещиноватости равна нулю.

Известен способ прогнозирования механических свойств горной породы [2], включающий измерение массовой доли минералов, находящихся в породе, определение их физико-механических характеристик, плотности и пористости. Зная пористость и массовую долю породы, определяют набор упругих коэффициентов, по которым прогнозируют состояние материала (породы). Недостатком известного способа является невысокая точность нахождения упругих коэффициентов и невозможность долгосрочного предсказания стадии разрушения массива исследуемого материала.

Известен способ определения напряженно-деформированного состояния материала [3], включающий отбор образцов материала, их нагружение и выявление предвестника разрушения материала. Недостатком известного способа является невозможность получения долгосрочного предсказания разрушения исследуемого материала.

Наиболее близким к предлагаемому техническому решению является способ определения напряженно-деформированного состояния материала (в том числе и с хрупким скелетом) [4], состоящий из отбора образцов материала, их нагружения и построения деформационной зависимости, выявления физико-механических характеристик материала и нахождения по зависимости «напряжение-деформация» коэффициентов, характеризующих предвестник разрушения материала. Недостатком известного способа является трудоемкость и невысокая точность в определении коэффициентов состояния материала, а также длительная обработка полученных результатов.

Задачей технического решения является снижение трудоемкости в определении коэффициентов состояния материала, упрощение и ускорение обработки полученных результатов.

Технический результат, получаемый при решении поставленной задачи, выражается в том, что имеется возможность характеризовать стадию состояния материала перед разрушением, что и является предвестником разрушения материала, путем сокращения времени измерения за счет уменьшения количества испытываемых образцов.

Поставленная задача решается следующим образом. В известном способе определения напряженно-деформированного состояния материала с хрупким скелетом, состоящем из отбора образцов материала, их нагружения и построения деформационной зависимости, выявления физико-механических характеристик материала и нахождения по зависимости «напряжение-деформация» коэффициентов, характеризующих предвестник разрушения материала, согласно изобретению при сжатии образцов определяют коэффициенты α p − , α_-, α_J, характеризующие изменение потенциальной энергии упругого деформирования при рассеянном разрушении материала, при этом предвестник разрушения материала ω находят по формуле

ω = α − I 1 + α J J + α p − Δ p − γ − ,

где α p − , α_-, α_J - постоянные коэффициенты, γ^- - положительный параметр, задающий квадратичную зависимость поверхностной энергии накопленного ансамбля микротрещин в хрупком материале, I₁ - относительное изменение объема материала, J - интенсивность касательных деформаций, Δp - изменение внутрипорового давления.

Кроме того, зависимость «напряжение-деформация» получают в виде кривой, которая имеет излом, делящий кривую на два участка, первый до излома и второй после излома, тогда коэффициент α p − находят по положению излома при всестороннем сжатии насыщенных флюидом образцов при поддержании постоянного давления в порах в течение всего испытания, коэффициент α_J находят по углу наклона участков кривой «осевое напряжение-осевая деформация» при одноосном сжатии и из зависимости «всестороннее давление-объемная деформация» при всестороннем сжатии ненасыщенных флюидом образцов, коэффициент α_- находят по углу наклона участков кривой «всестороннее давление-объемная деформация» при всестороннем сжатии ненасыщенных флюидом образцов, коэффициент γ^- находят по положению излома графика «всестороннее давление-объемная деформация» при всестороннем сжатии ненасыщенных флюидом образцов.

Кроме того, коэффициент α p − вычисляют из уравнения α p − = γ − − e p ∗ ( t g θ ν 1 − t g θ ν 2 ) 1 2 p , коэффициент α_J вычисляют из уравнения α J = 3 / 2 ( ( t g θ ν 1 − t g θ ν 2 ) 1 / 2 − ( t g θ c 1 − t g θ c 2 ) 1 / 2 ) , коэффициент α_- вычисляют из уравнения α_-=(tgθ_ν1-tgθ_ν2)^1/2, коэффициент γ^- вычисляют из уравнения γ − = e p ∗ ( t g θ ν 1 − t g θ ν 2 ) 1 2 , где θ_ν1 - угол наклона первого участка, θ_ν2 - угол наклона второго участка зависимости «всестороннее давление-объемная деформация» при всестороннем сжатии, e^∗ - относительное изменение объема, соответствующее излому кривой, θ_c1 - угол наклона первого участка, θ_c2 - угол наклона второго участка кривой зависимости «вертикальная нагрузка-вертикальная деформация» при одноосном сжатии.

Сравнение признаков заявленного технического решения с известными аналогичного назначения свидетельствует о соответствии его критерию «новизна». Признак - нахождение предвестника разрушения материала после испытания образцов по формуле: ω = α − I 1 + α J J + α p − Δ p − γ − обеспечивает уменьшение количества испытываемых образцов (для определения состояния напряженно-деформированного материала с хрупким скелетом), а значит снижает трудоемкость, упрощает и ускоряет обработку полученных результатов. Дополнительные признаки показывают конкретные способы достижения заявленных результатов.

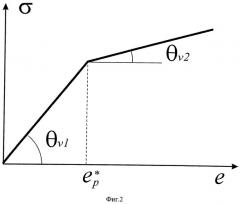
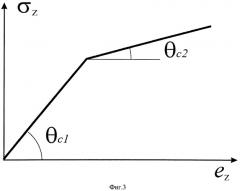
Техническая сущность предложенного решения поясняется чертежами, где на фиг.1 дан вид границы зоны упругости, на фиг.2 дана зависимость «напряжение-деформация» при всестороннем сжатии, на фиг.3 дана зависимость «осевое напряжение-осевая деформация» при одноосном сжатии.

Пример конкретного выполнения способа определения напряженно-деформированного состояния материала с хрупким скелетом.

Уровень трещиноватости характеризует состояние материала под нагрузкой и может считаться параметром предвестника разрушения материала с хрупким скелетом ω = α ± I 1 + α J J + α p ± Δ p − γ ± . Т.к. горные породы находятся в состоянии сжатия горным давлением, то предвестник разрушения материала ω зависит только от отрицательных коэффициентов, которые находят после испытания отобранных образцов исследуемого материала при их сжатии. Поэтому предвестник разрушения материала находят по формуле: ω = α − I 1 + α J J + α p − Δ p − γ − . Для определения коэффициентов состояния вещества ( α p − , α_-, α_J, γ^-) на трехосной испытательной машине проводят всестороннее сжатие образцов исследуемого материала, как насыщенных флюидом, так и без него, а на другой испытательной машине с вертикальной нагрузкой проводят одноосное сжатие образцов этого же материала.

При всестороннем сжатии ненасыщенного флюидом (сухого) образца получается график (как на фиг.2) - всестороннее напряжение σ - относительное изменение объема e, который имеет два участка: первый (до излома) - линейный, соответствующий упругому поведению материала образца, второй (после излома) - «квазилинейный» с меньшим углом наклона, соответствует поведению материала при развитии трещиноватости. Следует заметить, что не для всех материалов кривая σ-e имеет линейные участки с выраженным изломом, поэтому точку перегиба находят по второй производной, а участки считают квазилинейными. Коэффициент α_- определяется по разности тангенсов углов наклона этих участков

α − = ( t g θ ν 1 − t g θ ν 2 ) 1 / 2 ,                             ( 7 )

где θ_ν1 - угол наклона первого участка, θ_ν2 - угол наклона второго участка.

Коэффициент γ^- определяется по положению точки излома графика:

γ − = e p ∗ ( t g θ ν 1 − t g θ ν 2 ) 1 2 ,                       ( 8 )

где e^∗ - относительное изменение объема, соответствующее точке излома графика.

Коэффициент α_J (фиг.3) определяется по разности тангенсов углов наклона tgθ_c1-tgθ_c2 двух квазилинейных участков на графике вертикальная нагрузка σ_z - вертикальная деформация e_z при одноосном сжатии

α J = 3 / 2 ( ( t g θ ν 1 − t g θ ν 2 ) 1 / 2 − ( t g θ c 1 − t g θ c 2 ) 1 / 2 ) ,                       ( 9 )

где θ_c1 - угол наклона первого участка, θ_c2 - угол наклона второго участка на фиг.3.

Коэффициент α p − измеряется при испытании насыщенных флюидом образцов при постоянном давлении в порах за время всего испытания и вычисляется из уравнения

α p − = γ − − e p ∗ ( t g θ ν 1 − t g θ ν 2 ) 1 2 p ,                        ( 10 )

где p - давление флюида в порах образца, e p ∗ - положение точки излома на графике всестороннее напряжение σ - относительное изменение объема e, при давлении p, θ_ν1 - угол наклона первого участка, θ_ν2 - угол наклона второго участка, как на графике фиг.2.

Сведения, подтверждающие возможность осуществления изобретения

Существуют испытательные машины объемного и осевого сжатия [5], позволяющие реализовать предлагаемый способ, т.е. строить графики зависимости всестороннее давление - объемная деформация при всестороннем сжатии (как сухого материала, так и заполненного флюидом) и вертикальная нагрузка - вертикальная деформация при одноосном сжатии, для вычисления коэффициентов энергетического состояния материала (массива, породы), по которым находится предвестник разрушения материала ω.

Источники информации

1. Извеков О.Я., Кондауров В.И. О рассеянном разрушении пористых материалов с хрупким скелетом. // Механика твердого тела. №3, 2010.

2. Заявка США №20110022320, МПК G01V 9/00, 27.01.2011.

3. Патент RU №2234073, МПК G01N 3/00, 2004.

4. Патент RU №2322657, МПК G01N 3/00, 2005.

5. Болдырев Г.Г. Методы определения механических свойств грунтов. Пенза. 2008.

1. Способ определения напряженно-деформированного состояния материала с хрупким скелетом, состоящий из отбора образцов материала, их нагружения и построения деформационной зависимости, выявления физико-механических характеристик материала и нахождения по зависимости «напряжение-деформация» коэффициентов, характеризующих предвестник разрушения материала, отличающийся тем, что при сжатии образцов определяют коэффициенты α p − , α_-, α_J, характеризующие изменение потенциальной энергии упругого деформирования при рассеянном разрушении материала, при этом предвестник разрушения материала ω находят по формуле ω = α _ I 1 + α J J + α p − Δ p − γ − ,где α p − , α_-, α_J - постоянные коэффициенты, γ^- - положительный параметр, задающий квадратичную зависимость поверхностной энергии накопленного ансамбля микротрещин в хрупком материале, I₁ - относительное изменение объема материала, J - интенсивность касательных деформаций, Δp - изменение внутрипорового давления.

2. Способ по п. 1, отличающийся тем, что зависимость «напряжение-деформация» получают в виде кривой, которая имеет излом, делящий кривую на два участка, первый до излома и второй после излома, причем коэффициент α p − находят по положению излома при всестороннем сжатии насыщенных флюидом образцов, коэффициенты α_J и α_- находят по углу наклона участков кривой «осевое напряжение-осевая деформация» при одноосном сжатии и из зависимости «всестороннее давление-объемная деформация» при всестороннем сжатии ненасыщенных флюидом образцов, коэффициент γ^- находят по положению излома графика «всестороннее давление-объемная деформация» при всестороннем сжатии ненасыщенных флюидом образцов.

3. Способ по п. 2, отличающийся тем, что коэффициент α p − вычисляют из уравнения α p − = γ − − e p ∗ ( t g θ ν 1 − t g θ ν 2 ) 1 2 p , коэффициент α_J вычисляют из уравнения α J = 3 / 2 ( ( t g θ ν 1 − t g θ ν 2 ) 1 / 2 − ( t g θ c 1 − t g θ c 2 ) 1 / 2 ) , коэффициент α_- вычисляют из уравнения α_-=(tgθ_ν1-tgθ_ν2)^1/2, коэффициент γ^- вычисляют из уравнения γ − = e p ∗ ( t g θ ν 1 − t g θ ν 2 ) 1 2 , где θ_ν1 - угол наклона первого участка, θ_ν2 - угол наклона второго участка зависимости «всестороннее давление-объемная деформация» при всестороннем сжатии, e^∗ - относительное изменение объема, соответствующее излому кривой, θ_c1 - угол наклона первого участка, θ_c2 - угол наклона второго участка кривой зависимости «вертикальная нагрузка-вертикальная деформация» при одноосном сжатии.