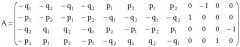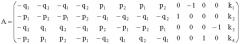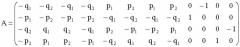Способ определения параметров волнового твердотельного гироскопа

Способ определения параметров волнового твердотельного гироскопа

Иллюстрации

Показать все

Реферат

Изобретение относится к области приборостроения и может быть использовано при изготовлении и подготовке к работе волнового твердотельного гироскопа (ВТГ), предназначенного для инерциальных навигационных систем и систем управления подвижных объектов.

Большое количество работ затрагивает вопрос идентификации производственных погрешностей изготовления резонаторов и методы повышения точности ВТГ. Вот некоторые из них: Матвеев В.А., Липатников В.И., Алехин А.В. Проектирование волнового твердотельного гироскопа / М.: Изд-во МГТУ им. Н.Э. Баумана. 1997; Гавриленко А.Б., Меркурьев И.В., Подалков В.В. Экспериментальные методы определения параметров вязкоупругой анизотропии резонатора волнового твердотельного гироскопа Вестник МЭИ, 2010, №5. Предлагаемые способы определения параметров используются при малых амплитудах колебаний, при которых отношение сигнала к шуму не достаточно высокое. При повышенных амплитудах колебаний отношение сигнала к шуму повышается, но при этом возрастают погрешности, вызванные нелинейностью колебаний. Это обстоятельство не позволяет идентифицировать параметры с высокой точностью.

Известен способ определения параметров волнового твердотельного гироскопа, заключающийся в том, что измеряют амплитуды колебаний резонатора на частотах вблизи резонанса в стационарных режимах (см. Журавлев В.Ф. Задача идентификации погрешностей обобщенного маятника Фуко // Изв. РАН. МТТ. 2000. №5. С.5-9). Определяются следующие параметры: коэффициенты неравножесткости, разнодобротности, демпфирования, ориентация главных осей упругой и вязкоупругой анизотропии, величина начального систематического ухода. При этом для нахождения параметров гироскопа используются линейные калибровочные уравнения.

Однако существующий способ определения параметров волнового твердотельного гироскопа не полностью реализует возможность получения оценок параметров с повышенной точностью. Это вызвано пренебрежением нелинейностью, которое возможно лишь при малых амплитудах колебаний, не превышающих одну десятую рабочего зазора. В этом случае отношение сигнала к шуму недостаточно высокое. Для его повышения следует увеличивать амплитуду колебаний. Однако при этом возрастают погрешности, вызванные нелинейностью, которые не учитываются.

Технической задачей настоящего изобретения является повышение точности определения параметров ВТГ. Полученные данные о параметрах используются для аналитической компенсации погрешностей гироскопа и для балансировки резонатора. Данные о параметрах позволят значительно улучшить одну из основных характеристик гироскопа - точность определения угловой скорости.

Технический эффект, заключающийся в учете нелинейности при повышенных амплитудах колебаний резонатора ВТГ, достигается тем, что в известном способе определения параметров волнового твердотельного гироскопа, а именно коэффициента демпфирования γ, угловой скорости ν, коэффициентов упругой анизотропии g_c и g_s, коэффициентов, характеризующих жесткость резонатора с и n, коэффициентов расщепления частот h_c и h_s, параметров внешнего воздействия на резонатор b₁, b₂, b₃, b₄, заключающемся в том, что измеряют емкостной системой электродов медленные переменные p₁, q₁, p₂, q₂ на частотах ω вблизи частоты резонанса ω₀ в стационарных режимах, измеренные значения медленных переменных и частотных расстроек λ=(ω-ω₀)/ω₀ используют при формировании вектора b=(2λp₁,-2λq₁,2λp2,-2λq₂)^T и матрицы

A = ( − q 1 − q 2 − q 1 − q 2 − p 1 − p 2 − p 1 − p 2 − q 2 q 1 q 2 − q 1 − p 2 p 1 p 2 − p 1   p 1 p 2 p 1 p 2 − q 1 − q 2 − q 1 − q 2 p 2 − p 1 − p 2 p 1 − q 2 q 1 q 2 − q 1   0 − 1 0 0 1 0 0 0 0 0 0 − 1 0 0 1 0 )

согласно изобретению увеличивают в два-три раза амплитуды колебаний резонатора, матрицу дополняют столбцом элементов k₁ k₂, k₃, k₄, нелинейных относительно медленных переменных, где k₁=-p₁E-q₂K, k₂=q₁E-p₂K, k₃=-p₂E+q₁K, k₄=q₂E+p₁K,

E = ( q 1 2 + p 1 2 + q 2 2 + p 2 2 / 8 ) , K=(p₂q₁-p₁q₂)/4, и вычисляют параметры волнового твердотельного гироскопа одновременно с коэффициентом нелинейности колебаний ξ по формуле x=(A^TA)^-1A^Tb, где х=(γ, ν, g_c, g_s, c, n, h_c, h_s, b₁, b₂, b₃, b₄, ξ)^T - вектор определяемых параметров.

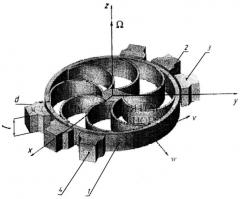
Изобретение поясняется рисунком, который не охватывает и, тем более не ограничивает весь объем притязаний данного технического решения, а является лишь иллюстрирующим материалом частного случая выполнения ВТГ, микромеханическая реализация ВТГ.

Гироскоп состоит из тонкого упругого кольцевого резонатора 1, связанного с основанием торсионами 2, электростатического электрода измерения нормального прогиба 3 и электрода возбуждения колебаний 4. Резонатор 1 изготовлен методом литографии совместно с торсионами 2 упругого подвеса и электронным контуром управления из поликристаллического кремния. Его подробное описание приведено в книге Меркурьева И.В., Подалкова В.В. Динамика микромеханического и волнового твердотельного гироскопов. М.: ФИЗМАТЛИТ, 2009, 228 с., на 86 стр.

Нормализованные дифференциальные уравнения колебаний неидеального резонатора по второй основной форме запишем в стандартной форме одночастотной системы:

x ¨ + x = q ( τ , x , x ˙ ) ,                                           (1)

здесь х=(f, g)^T - обобщенные координаты, определяющие колебания резонатора по второй основной форме, в (1) и далее точкой обозначено дифференцирование по безразмерному времени τ=ωt;

q - вектор малых обобщенных сил, возмущающих движение резонатора:

q = − ( C + N + H ) x − ( D + G + F ) x ˙ + ξ ( x , x ) x + u ( t ) ,

C = c ( 1 0 0 1 ) , N = n ( 0 1 − 1 0 ) , H = h ( cos 4 ψ sin 4 ψ sin 4 ψ − cos 4 ψ ) ,

D = γ ( 1 0 0 1 ) , G = ν ( 0 1 − 1 0 ) , F = g ( cos 4 ψ * sin 4 ψ * sin 4 ψ * − cos 4 ψ * ) ,

u ( t ) = ( b 1 cos μ τ b 2 sin μ τ b 3 cos μ τ b 4 sin μ τ ) ,

где C и H симметрические матрицы потенциальных сил сферического и гиперболического типа, N - кососимметрическая матрица непотенциальных сил, D и F - симметрические матрицы диссипативных сил сферического и гиперболического типа, G - кососимметрическая матрица гироскопических сил, матрицы Н и F имеют след, равный нулю (девиаторы), γ - коэффициент демпфирования, ν - начальная угловая скорость. Коэффициенты g и h определяют нормы девиаторов гиперболических сил, характеризующие вязкую и упругую анизотропию. Углы ψ и ψ* определяют ориентацию главных осей упругой и вязкоупругой анизотропии по отношению к основанию гироскопа. Параметр ξ обусловлен нелинейными эффектами ММГ. Параметры b_i (i=1, 2, 3, 4) характеризуют направление, амплитуду и фазу внешнего воздействия на резонатор. Величина µ=ω₀/ω=1+λ, λ - малая нормализованная частотная расстройка.

Отметим, что слагаемое ξ(x,x)x формулы получено в книге Меркурьева И.В., Подалкова В.В., в предположении, что напряжение, возникающее при окружной деформации, подчиняется нелинейному закону. В результате замены переменных по формулам

f = q 1 cos μ τ + p 1 sin μ τ ,   f ˙ = − q 1 sin μ τ + p 1 cos μ τ , g = q 2 cos μ τ + p 2 sin μ τ ,   g ˙ = − q 2 sin μ τ + p 2 cos μ τ ,                 (2)

в системе (1) и осреднения по методу Крылова - Боголюбова, получим систему дифференциальных уравнений в медленных переменных

2 p ˙ = A x − b ,                                                                               (3)

где p=(q_],p_l,q₂,p₂)^T,

A = ( − q 1 − q 2 − q 1 − q 2 − p 1 − p 2 − p 1 − p 2 − q 2 q 1 q 2 − q 1 − p 2 p 1 p 2 − p 1   p 1 p 2 p 1 p 2 − q 1 − q 2 − q 1 − q 2 p 2 − p 1 − p 2 p 1 − q 2 q 1 q 2 − q 1   0 − 1 0 0 1 0 0 0 0 0 0 − 1 0 0 1 0   k 1 k 2 k 3 k 4 ) ,

x=(γ, ν, g_c, g_s, c, n, h_c, h_s, b₁, b₂, b₃, b₄, ξ)^T - вектор параметров,

b=(2λp₁, -2λq₁, 2λp₂, -2λq₂) - измеряемый вектор,

g_S=gsin4ψ*, g_c=gxos4ψ*, h_s=hsin4ψ, h_c=hcos4ψ,

k₁=-p_lE-q₂K, k₂=q₁E-p₂K, k₃=-p₂E+q₁K, k₄=q₂E+p₁K,

E = 3 ( q 1 2 + p 1 2 + q 2 2 + p 2 2 ) / 8 , K=(p₂q₁-p₁q₂)/4.

Для целей идентификации параметров математической модели (3) рассмотрим стационарный режим вынужденных колебаний резонатора, определяемый алгебраической системой уравнений, полученной из (3) при значениях p ˙ = 0 :

A x − b = 0                                                                            (4)

В системе алгебраических уравнений (4) измеряемыми являются стационарные значения p₁, q₁, p₂, q₂, полученные при заданной частотной расстройке λ. Перепишем уравнения (4) с учетом ненаблюдавшихся в эксперименте случайных ошибок

b = A x + e ,                                                                              (5)

где e=(e₁, e₂, e₃, e₄) - вектор случайных ошибок.

Составим переопределенную алгебраическую систему уравнений из блоков (5), соответствующих заданной частотной расстройке.

Для идентификации параметров системы (5) необходимо выбрать такие значения расстройки λ, для которых матрица C=A^TA не является вырожденной.

По методу наименьших квадратов получим оценку x ^ параметров математической модели

x ^ = ( A T A ) − 1 A T b

Искомые оценки минимизируют сумму квадратов отклонений

S о с т = ( b − A x ^ ) T ( b − A x ^ )

и остаточную дисперсию σ ^ о с т 2 = S о с т / ( n − k )

где n - число уравнений, k - число идентифицируемых параметров.

Перейдем к интервальной оценки регрессионной модели.

Предположим, что случайная величина e_i имеет нулевое математическое ожидание M[e_i]=0, во всех опытах дисперсия ошибки е одинакова D [ e i ] = σ e 2 , ошибки в отдельных опытах не зависят друг от друга cov[e_ie_j]=M[e_ie_j]=0 для i≠j и M [ e i 2 ] = D [ e i ] = σ e 2 , случайная величина подчиняется нормальному закону распределения, т.е. e ~N(0, σ e 2 ,I) , I - единичная матрица.

Доверительный интервал находим по формуле, представленной в книге Бородюка В.П. Статистические методы математического описания сложных объектов. - М.: МЭИ, 1981. - 91 с.на 42 стр.

x ^ j − t γ σ ^ о с т c i j ≤ x j ≤ x ^ j + t γ σ ^ о с т c i j ,                    (6)

где t_γ - число, выбираемое из таблицы функций Лапласа. Для уровня надежности γ=0.95 число t_γ=1,96. Если число n-k мало, то t_γ выбирают по таблице распределения Стьюдента, c_ij - диагональные элементы матрицы C.

Рассмотрим два случая:

1-й линейных колебаний (ξ=0;, 2-й с учетом коэффициента нелинейности (ξ≠0).

Для оценки параметров математической модели использован 61 режим стационарных колебаний, представленный на фиг.2. Число уравнений системы равно n=244.

В первом случае определяются 12 параметров, т.е. k=12. Остаточная дисперсия равна σ ^ о с т 2 = 0 , 0874 . Во втором - k=13, σ ^ о с т 2 = 0 , 0848 .

Уменьшение остаточной дисперсии σ ^ о с т 2 более чем в десять раз при учете коэффициента нелинейности указывает на то, что математическая модель, рассмотренная во втором случае, является более адекватной и позволяет точнее определять параметры гироскопа.

Остаточное среднее квадратичное отклонение σ ^ о с т при этом снизилось в 3,2 раза. Из формулы (6), которая справедлива только для адекватной модели, следует, что во столько же раз уменьшились доверительные интервалы и повысилась точность определения параметров ВТГ. Однако без учета нелинейности математическая модель не является адекватной. Проведенные численные расчеты показали, что точность определения параметров повышается более чем в 3,2 раза.

Таким образом, разработана методика определения параметров гироскопа с учетом нелинейности колебаний кольцевого резонатора. Эта методика позволяет проводить испытания при больших амплитудах колебаний, при которых отношение сигнала к шуму достаточно высокое. Результаты обработки экспериментальных данных показали, что учет нелинейности значительно повышает точность определения параметров.

Использование коэффициентов нелинейности при аналитической компенсации позволит существенно повысить точность.

Способ определения параметров волнового твердотельного гироскопа, а именно коэффициента демпфирования γ, начальной угловой скорости v, коэффициентов упругой анизотропии g_c и g_s , коэффициентов, характеризующих жесткость резонатора с и n, коэффициентов расщепления частот h_c и h_s, параметров внешнего воздействия на резонатор b₁, b₂, b₃, b₄, заключающийся в том, что измеряют емкостной системой электродов медленные переменные p₁, q₁, p₂, q₂ на частотах со вблизи частоты резонанса ω₀ в стационарных режимах, измеренные значения медленных переменных и частотных расстроек λ=(ω-ω₀)/ω₀ используют при формировании вектора b=(2λp₁, -2λq₁, 2λp2, -2λq₂)^T и матрицы A = ( − q 1 − q 2 − q 1 − q 2 − p 1 − p 2 − p 1 − p 2 − q 2 q 1 q 2 − q 1 − p 2 p 1 p 2 − p 1   p 1 p 2 p 1 p 2 − q 1 − q 2 − q 1 − q 2 p 2 − p 1 − p 2 p 1 − q 2 q 1 q 2 − q 1   0 − 1 0 0 1 0 0 0 0 0 0 − 1 0 0 1 0 ) отличающийся тем, чтоувеличивают в два-три раза амплитуды колебаний резонатора, измеряют медленные переменные не менее чем на четырех различных частотах вблизи резонанса, матрицу дополняют столбцом элементов k₁, k₂, k₃, k₄ нелинейных относительно медленных переменных, где k₁=-p₁E-q₂K, k₂=q₁E- p₂K, k₃=-p₂E+q₂k, k₄=q₂E+p₁K, E = ( q 1 2 + p 1 2 + q 2 2 + p 2 2 / 8 ) , K=(p₂q₁-p₁q₂)/4 и вычисляют параметры волнового твердотельного гироскопа одновременно с коэффициентом нелинейности колебаний ξ по формуле х=(A^TA)^-1A^Tb, где х=(γ, ν, g_c, g_s, c, n, h_c, h_s, b₁, b₂, b₃, b₄, ξ)^T - вектор определяемых параметров, A и b - матрица и вектор, составленные из матриц A_i и векторов b_i.