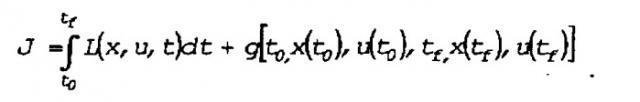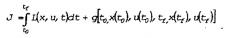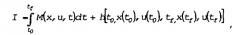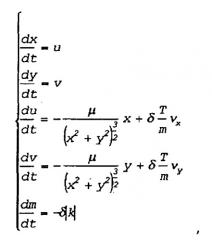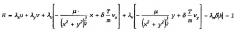Адаптивный способ оптимизации с множественной пристрелкой для определения оптимальных траекторий космического летательного аппарата

Адаптивный способ оптимизации с множественной пристрелкой для определения оптимальных траекторий космического летательного аппарата

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Настоящее изобретение относится к определению оптимальных траекторий перемещения космического летательного аппарата и может использоваться для решения широкого круга задач, задействующих оптимизацию траекторий перемещения космических летательных аппаратов, например космических кораблей, ракет, космических челноков и т.д.

В частности настоящее изобретение позволяет определять оптимальную траекторию перемещения в данном диапазоне эпохи, причем оптимальная траектория перемещения позволяет, в целом, отвечать требованию данной космической миссии и, в частности, минимизировать время перемещения, расход топлива или комбинацию их обоих.

УРОВЕНЬ ТЕХНИКИ

Как показано, в литературе дается определение наилучшей траектории космического летательного аппарата для данной миссии как "двухточечной краевой задачи", и она состоит в определении траектории, среди всех возможных, соединяющей две разные точки в пространстве (представляющие граничные условия) и позволяющей максимизировать или минимизировать данную функцию стоимости (также именуемую индексом стоимости). Уравнения движения являются дифференциальными ограничениями задачи.

Известно несколько способов оптимизации, полезных для решения задач оптимизации, связанных с космическими перемещениями, которые делятся, по существу, на две основные категории:

- классические, косвенные способы на основе принципа максимума Понтрягина; и

- прямые способы, которые пытаются найти минимум функции стоимости многими численными методами и могут дополнительно группироваться в

прямые способы, применяемые в вариационном исчислении, и

методы поиска.

Генетические алгоритмы также применяются для решения задач, связанных с межпланетными перемещениями.

Ниже приведено краткое описание вышеперечисленных известных способов.

Принцип максимума Понтрягина является основной теоремой вариационного исчисления, применяемой к теории оптимального управления: он дает некоторые необходимые условия для определения оптимального решения анализируемой задачи, и он основан только на дифференциальных свойствах, которые определенные классы функций демонстрируют в точках экстремума. Согласно таким условиям можно определять развитие во времени некоторых параметров, так называемых множителей Лагранжа, используемых для оценивания переменных управления, необходимых для решения задачи оптимизации. Начальные значения множителей Лагранжа неизвестны, и их можно оценивать численно, чтобы удовлетворять граничным условиям. Другими словами, задача оптимизации полностью сводится к определению начальных значений множителей Лагранжа. Задача становится еще более сложной, когда конечное состояние не полностью определено, то есть некоторые переменные вектора состояния не назначены на граничных условиях. Помимо условий, заданных принципом максимума Понтрягина, следует рассматривать дополнительные ограничения, заданные как "условия трансверсальности".

В частности косвенные способы посредством условий, заданных принципом максимума Понтрягина, позволяют определить в ходе выполнения, какой путь является наилучшим для использования переменных управления для решения задачи оптимизации, но такие переменные в начале неизвестны, как показано ниже.

Пусть

x ˙ = f ( x , u , t )

- это система дифференциальных уравнений в частных производных первого порядка, где х - вектор состояния, и u - так называемый вектор управления, то есть вектор, определяемый в ходе выполнения для минимизации или максимизации данной функции стоимости J. Обращаясь к формулировке задачи Больца, функция стоимости может иметь вид:

Предположим, например, что функцию стоимости J нужно минимизировать. Это приводит к следующему условию

Пусть также H(x, u, λ, t) является функцией Гамильтона, связанной с системой, выраженной в форме:

H ( x , u , λ , t ) = λ T x ˙ − L . Заметим, что если нужно максимизировать другой данный функционал I, заданный как:

предыдущие формулы принимают вид:

и

где λ - вектор множителей Лагранжа (который также задан как вектор косостояния или вектор сопряженной переменной). Принцип максимума Понтрягина утверждает, что если x(t), λ(t) удовлетворяют условия:

и для всех

то u* является желаемым оптимальным управлением, которое максимизирует функцию Гамильтона H.

Помимо принципа максимума Понтрягина, если вектор состояния не полностью определен на границах, необходимо добавить дополнительные условия под названием "условия трансверсальности". Количество этих дополнительных ограничений равно количеству составляющих в векторе состояния, которые не определены на границах. Например, если конечный момент времени не установлен, соответствующее условие трансверсальности должно быть:

H_f=1,

если рассмотреть задачу минимального времени перемещения, или:

H_f=0,

если анализируется задача минимального расхода топлива.

Количество и выражение условий трансверсальности изменяется согласно данной анализируемой задаче.

Применим вышеприведенную общую формулировку к двухточечной задаче, в случае межпланетных перемещений, например, рассмотрим перемещение Земля-Марс. Согласно гипотезе копланарного движения (все орбиты основных тел в Солнечной системе имеют малый наклон относительно плоскости Эклиптики) и, рассматривая инерциальную систему координат xOy, где начало отсчета О совпадает с центром масс Солнца, уравнения движения можно записать следующим образом:

где {x, y, u, v, m} - вектор состояния (х, у - компоненты вектора положения, a u, v - компоненты вектора скорости; m фактическая масса космического летательного аппарата), µ - гравитационный параметр Солнца, Т - уровень тяги, достижимый на данной силовой установке (непрерывного маневрирования) и δ - функция включения-отключения, представляющая состояние силовой установки (δ=0 - двигатель отключен; δ=1 - двигатель действует), {v_x, v_y} - единичный вектор, указывающий направление тяги. Для данных времени вылета t₀ и времени прилета t_f космического летательного аппарата можно также определить функционал

который нужно минимизировать (т.е. нужно минимизировать время перемещения); соответствующая функция Гамильтона должна принять вид:

или более удобным образом:

где {λ_х,λ_y,λ_u,λ_v} - вектор множителей Лагранжа (вектор косостояния). Применим принцип максимума Понтрягина. Управление является оптимальным, если и только если:

и

Первое условие утверждает, что направление вектора тяги {v_x, v_y} должно быть выровнено с вектором {λ_u, λ_v}, а второе условие указывает, удобно ли включать маневровый двигатель. В отношении производных косостояния, принцип максимума Понтрягина утверждает, что:

Если все эти условия выполняются, принцип максимума Понтрягина полностью удовлетворяется, и оптимальное направление тяги задается аналитически через переменные косостояния λ_u, λ_v. Основная проблема, оказывающая влияние на этот подход, состоит в том, что начальные значения {λ_х, λ_y, λ_u, λ_v, λ_m,} неизвестны и не поддаются оценке из физических соображений; можно лишь предположить порядок величины каждого члена, исходя из соответствующей производной. Безусловно, существует ограниченное количество оптимальных векторов {λ_х,0, λ_y,0, λ_u,0, λ_v,0, λ_m,0}, которые нужно искать в ℜ⁵ (или в ℜ⁷, если гипотеза копланарного движения неверна), позволяющих достичь желаемых конечных условий. Ясно, что такой подход, хотя он дает аналитическое выражение для оптимальных направления и величины тяги, выглядит весьма неудовлетворительным ввиду трудности достижения конечных условий.

Напротив, прямые способы, применяемые в вариационном исчислении, основаны на аппроксимации вектора состояния и функционала стоимости через представления последовательности. Выбрав надлежащее множество элементарных функций для представления последовательности, на основании данных гипотез, можно найти неизвестные коэффициенты последовательности путем нахождения экстремума приближенного функционала стоимости. Другими словами, задача нахождения экстремума функционала на множестве функций сводится к нахождению экстремума функции на множестве параметров. Полученное решение является, в целом, приближенным решением, если множество параметров не является бесконечным множеством.

В частности, такого рода прямые способы призваны сводить задачу максимизации (или минимизации) функционала относительно функции к задаче максимизации (или минимизации) функции на множестве переменных через представления последовательности, хотя полученное решение является, в целом, приближенным решением, если множество параметров не является бесконечным множеством. Рассмотрим 1-мерную дифференциальную задачу, выраженную в форме x ˙ = f ( x , u , t ) , где х - вектор состояния и u - вектор управления. Пусть также J(x) - функционал, подлежащий максимизации или минимизации. Способы аппроксимации последовательностью основаны на предположении о том, что функцию x=x(t), обеспечивающую максимум (или минимум) функционала J(x), можно разложить в ряд в виде:

и также

где a_k - коэффициенты, не зависящие от времени, и ψ_k(t} известные функции. Ясно, что нужно применять усеченные формы предыдущих выражений:

Предполагается, что эта последовательность аппроксимирующих функций полна для функций x(t). По определению, последовательность аппроксимирующих функций полна при следующем условии: для всех ε>0 существует целое число j, для которого:

Важность этого определения заключается в том, что

если J(x) строго непрерывен и если последовательность функций полна. Приближенный функционал J_n(x_n) должен принимать форму:

Для решения задачи оптимизации J_n(x_n) должен быть стационарным относительно каждого a_k, то есть:

Выполнив указанные интегрирования, результирующую систему уравнений можно решить для стационарных точек, и эти стационарные точки, которые являются относительными максимумами (или минимумами), можно определить методами поиска. Функционал J_n(x_n) часто выражают следующим образом:

Кроме того, методы поиска основаны на численных методах для оценивания оптимального решения, начиная с приближенного оценивания функции стоимости. Получив такую аппроксимацию, можно искать множество переменных, максимизирующих (или минимизирующих) функцию стоимости в данной области; поэтому такие способы также называются "методам поиска". Функцию можно задавать аналитически или определять экспериментально; она может иметь или не иметь разрывы, и могут существовать ограничительные уравнения, ограничивающие аргументы меры производительности. В последнем случае задача называется задачей "нелинейного программирования". Среди методов поиска максимума (или минимума) следует упомянуть способы градиентного поиска, одномерного поиска и непоследовательного поиска.

Кроме того, генетические алгоритмы представляют собой методы поиска, используемые для нахождения точных или приближенных решений задач оптимизации и поиска. Они принадлежат широкому классу эволюционных алгоритмов, которые используют теоретические построения, инспирированные эволюционной теорией в биологии, например, наследственность, мутация, селекция и кроссинговер. Для решения задачи оптимизации выбирается несколько множеств, состоящих из двух или более параметров управления, именуемых хромосомами; после построения хромосом имеют место случайные "совпадения" между хромосомами, и благодаря кроссинговеру порождаются новые хромосомы (потомки), будем надеяться, более близкие к желаемому решению. Кроссинговеры происходят согласно данным правилам. Затем весь процесс повторяется до тех пор, пока не будут получены значительные усовершенствования; таким образом, алгоритм находит оптимальное решение.

Всем вышеописанным методам оптимизации присущи внутренние ограничения, ограничивающие их применимость данной задачей или их эффективность при нахождении решения.

Кроме того, заявитель обратил внимание на то, что "двухточечная краевая задача" применительно к перемещениям космических летательных аппаратов, не только межпланетным, оказалась более сложной, чем предполагалось (этот результат будет описан ниже), и это сильно влияет на действенность каждого вышеописанного способа.

Что касается косвенных способов, хотя выполняются некоторые аналитические ограничения по оптимальности, не удается заранее установить значение начальных множителей Лагранжа, позволяющее отвечать граничным условиям. Трехмерный анализ двухточечной задачи оптимизации потребовал бы шести множителей для вектора состояния космического летательного аппарата, плюс одинсоответствующий его массе. Кроме того, если начальная эпоха является параметром для оптимизации, также следует рассматривать начальный момент t₀ для начала миссии. Что касается начальной эпохи t₀, может быть важно подчеркнуть, что при рассмотрении межпланетных перемещений, в особенности при анализе перемещений среди внутренних планет, выбор начальной эпохи t₀ играет важнейшую роль в планировании миссии, поскольку эпоха определяет взаимное расположение начальной и целевой точек. Если взаимное расположение не выбрано правильно, космическая миссия также может окончиться неудачей.

Поэтому, что касается косвенных способов, до восьми переменных для оптимизации можно включать в анализ для оптимизации, и это приводит к большим затратам времени вычисления.

Что касается прямых способов, применяемых в вариационном исчислении, весьма трудно получить аналитическое выражение для ошибки, вносимой вышеописанной процедурой, поэтому трудно оценить, сходится ли аппроксимация функции стоимости, из-за чего трудно понять, совпадает ли приближенное решение с реальным поведением оптимального решения. Кроме того, анализ N-мерных задач, например межпланетного перемещения, требует большого количества интегрирований и коэффициентов, но всех этих усилий самих по себе может быть недостаточно для обеспечения удовлетворительного представления функционала стоимости вследствие взаимозависимости всех переменных в векторе состояния.

Другое ограничение, влияющее на подобные способы, состоит в том, что функционал стоимости, а также компоненты вектора состояния должны быть непрерывными в области интегрирования. Задачи, предусматривающие мгновенные изменения вектора состояния, например, переход между системами координат в ходе межпланетного перемещения или отход ступени при анализе траектории ракеты-носителя, не поддаются уверенному решению этими способами.

Градиентные способы основаны на определении градиента функции стоимости посредством нескольких оценок самой функции относительно данных параметров: чем лучше известен градиент функции, тем выше вероятность нахождения минимума (или максимума) в области поиска. Локальные минимумы можно получить быстро, если функция стоимости является гладкой относительно выбранных параметров; другие задачи, например оценивание траектории космического летательного аппарата, отличаются поразительно неправильным функционалом стоимости, что показано в дальнейшем. Поэтому градиентные методы поиска не могут быть надежными при рассмотрении подобных задач.

Способы одномерного поиска весьма просто и легко реализовать. Такие способы используют, например, те, кому приходится настраивать электрическую цепь, регулируя несколько параметров. Сначала один из параметров регулируется, пока не будет достигнуто дальнейшее улучшение; затем настраивается другой параметр, пока не будет достигнуто дополнительное улучшение, и т.д. После однократной регулировки каждого параметра процесс повторяется путем возврата к первому параметру и проведения вышеописанных операций. Согласно неправдоподобной гипотезе, что параметры не взаимодействуют друг с другом, эта процедура приводит к желаемой оптимальной конфигурации. Взаимозависимость среди переменных сильно влияет на области применения этой процедуры.

Непоследовательный поиск производится по равномерно разнесенным точкам в односвязной области евклидова пространства. Каждой из координат x_i назначается множество равномерно разнесенных точек, именуемых точками сетки, и используются только значения x_i в этих точках сетки. Затем оценивается функция стоимости для всех возможных комбинаций точек сетки, и значение сетки вектора х, обеспечивающее наилучшую f(x), считается выигрышным. Поисковик должен соответственно выбирать интервал сетки; что касается количества необходимых точек данных, если каждой координате x_i назначается k разнесенных точек, полный объем данных составляет kⁿ, где n - количество составляющих в х. Методы непоследовательного поиска не требуют предположений, касающихся резкости изменений вектора состояния и функционала стоимости, но большое количество необходимых оценок делает их совершенно неэффективными.

Рассмотрим теперь двухточечную краевую задачу и предположим, что полное время перемещения является функционалом, подлежащим минимизации. Общий метод, используемый для решения двухточечной задачи, состоит в минимизации

расширенной функции стоимости J ˜ , которая является взвешенной комбинацией самого функционала стоимости и нормы ошибки, оцененной на границах:

где (r_f-r_target) - разность между вектором конечного положения космического летательного аппарата и вектором целевого положения, (V_f-V_target) - разность между вектором конечной скорости космического летательного аппарата и вектором целевой скорости, и Y_f - угол полета, который должен быть близким к нулю, чтобы траектория перемещения космического летательного аппарата, в конце концов, проходила по касательной к целевой орбите при совпадении. Коэффициенты δr, δV, δγ представляют допуски, а также t_ref, вносимые для того, чтобы сделать функционал однородным. Такой функционал стоимости удобен для повышения правдоподобия сходимости к оптимальному решению при данных граничных ограничениях. Возникает проблема, состоящая в том, что такого рода функция демонстрирует две разные тенденции, которые делают нахождение оптимального решения очень трудным.

В частности, такого рода функция демонстрирует плавный макроскопический тренд и неправильное микроскопическое поведение, как показано на фиг. 1 и на фиг. 2, соответственно.

В частности, фиг. 1 демонстрирует пример макроскопического тренда расширенной функции стоимости J ˜ , который выглядит плавным в обширных областях пространства, а фиг. 2 демонстрирует пример микроскопического тренда расширенной функции стоимости J ˜ , в котором область вблизи начала отсчета насыщена большим количеством пиков и впадин.

Это представляет доказательство того факта, что двухточечная краевая задача часто бывает гораздо сложнее, чем предполагается, и сходимость к истинному оптимальному решению является крайне маловероятным событием, по меньшей мере, согласно вышеописанным известным алгоритмам оптимизации.

ЗАДАЧА И СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Заявитель провел тщательное исследование для определения возможности разработки эффективного, не требующего больших вычислительных затрат способа, позволяющего надежно определять оптимальные траектории перемещения космических летательных аппаратов.

Задачей настоящего изобретения является предоставление способа определения оптимальных траекторий перемещения космических летательных аппаратов, который позволяет решить вышеописанные проблемы известных методов и преодолеть препятствия, делающие известные алгоритмы неэффективными.

Эта задача решается настоящим изобретением, которое относится к способу определения оптимальной траектории перемещения космического летательного аппарата; программе программного обеспечения, содержащей участки кода программного обеспечения для реализации, при ее выполнении, упомянутого способа; программному продукту программного обеспечения, содержащему компьютерно-читаемый носитель, на котором хранится упомянутая программа программного обеспечения; электронному процессору, сконфигурированному для реализации упомянутого способа; и космическому летательному аппарату, содержащему электронный процессор, сконфигурированный для реализации упомянутого способа, как задано в прилагаемой формуле изобретения.

В частности, настоящее изобретение относится к способу определения траектории перемещения космического летательного аппарата, например космического корабля, ракеты, космического челнока и т.д., от начального космического тела к целевому космическому телу относительно данного центрального космического тела, причем определенная траектория является оптимальной в отношении того, чтобы перемещение космического летательного аппарата отвечало требованию данной космической миссии; причем способ содержит этапы, на которых:

- предоставляют, согласно принципу максимума Понтрягина, физико-математическую модель, связывающую модельные величины и физические величины, представляющие перемещение космического летательного аппарата относительно данного центрального космического тела, причем модельные величины содержат первую векторную величину модели и вторую векторную величину модели, причем первая векторная величина модели имеет первый модуль, изменяющийся во времени, и первую ориентацию в пространстве, которая изменяется во времени и задается первым углом долготы, изменяющимся во времени, и первым углом возвышения, изменяющимся во времени, причем первая векторная величина модели представляет, момент за моментом, соответствующее оптимальное направление тяги космического летательного аппарата относительно требования данной космической миссии, причем вторая векторная величина модели имеет второй модуль, изменяющийся во времени, и вторую ориентацию в пространстве, которая изменяется во времени и задается вторым углом долготы, изменяющимся во времени, и вторым углом возвышения, изменяющимся во времени, причем вторая векторная величина модели представляет, момент за моментом, развитие во времени первой векторной величины модели;

- устанавливают, в физико-математической модели, начальные и конечные граничные условия, причем начальные граничные условия таковы, что в начальный момент времени перемещения положение и скорость космического летательного аппарата близки к положению и скорости соответственно начального космического тела, причем конечные граничные условия таковы, что в конечный момент времени перемещения положение и скорость космического летательного аппарата близки к положению и скорости соответственно целевого космического тела;

- устанавливают, в физико-математической модели, первые условия так, что второй модуль связан с первым модулем через величину, связанную с угловой скоростью в зависимости от данного центрального космического тела;

- устанавливают, в физико-математической модели, вторые условия так, что конкретный угол долготы, между первым углом долготы и вторым углом долготы, и конкретный угол возвышения, между первым углом возвышения и вторым углом возвышения, не зависят друг от друга;

- рассматривают первые начальные моменты времени, включенные в данный временной диапазон, первые значения долготы конкретного угла долготы, включенные в данный диапазон долготы, и первые значения возвышения конкретного угла возвышения, включенные в данный диапазон возвышения; и

- определяют траекторию перемещения космического летательного аппарата на основании физико-математической модели, рассматриваемых первых начальных моментов времени, рассматриваемых первых значений долготы и рассматриваемых первых значений возвышения.

Предпочтительно определение траектории перемещения космического летательного аппарата на основании физико-математической модели, рассматриваемых первых начальных моментов времени, рассматриваемых первых значений долготы и рассматриваемых первых значений возвышения содержит этапы, на которых:

вычисляют значения данной функции стоимости, связанной с требованием данной космической миссии, причем значения данной функции стоимости вычисляются на основании рассматриваемых первых начальных моментов времени, рассматриваемых первых значений долготы и рассматриваемых первых значений возвышения;

определяют приближенную функцию стоимости на основании вычисленных значений данной функции стоимости;

вычисляют значения приближенной функции стоимости на основании рассматриваемых первых начальных моментов времени, рассматриваемых первых значений долготы и рассматриваемых первых значений возвышения;

идентифицируют, среди вычисленных значений приближенной функции стоимости, экстремальное значение приближенной функции стоимости и, среди рассматриваемых первых начальных моментов времени, среди рассматриваемых первых значений долготы и среди рассматриваемых первых значений возвышения, оптимальный начальный момент времени, оптимальное значение долготы и оптимальное значение возвышения соответственно на основании которых вычислено экстремальное значение приближенной функции стоимости; и

определяют траекторию перемещения космического летательного аппарата на основании физико-математической модели, идентифицированного оптимального начального момента времени, идентифицированного оптимального значения долготы и идентифицированного оптимального значения возвышения.

Более предпочтительно, способ согласно настоящему изобретению дополнительно содержит этапы, на которых:

- если траектория, определенная на основании физико-математической модели, рассматриваемых первых начальных моментов времени, рассматриваемых первых значений долготы и рассматриваемых первых значений возвышения, не отвечает начальным граничным условиям и конечным граничным условиям в пределах предварительно заданного допуска,

выбирают временной поддиапазон на основании данного временного диапазона и идентифицированного оптимального начального момента времени,

выбирают поддиапазон долготы на основании данного диапазона долготы и идентифицированного оптимального значения долготы,

выбирают поддиапазон возвышения на основании данного диапазона возвышения и идентифицированного оптимального значения возвышения,

рассматривают вторые начальные моменты времени, включенные в выбранный временной поддиапазон, вторые значения долготы конкретного угла долготы, включенные в выбранный поддиапазон долготы, и вторые значения возвышения конкретного угла возвышения, включенные в выбранный поддиапазон возвышения, и

определяют траекторию перемещения космического летательного аппарата на основании физико-математической модели, рассматриваемых вторых начальных моментов времени, рассматриваемых вторых значений долготы и рассматриваемых вторых значений возвышения.

В частности, выбор временного поддиапазона на основании данного временного диапазона и идентифицированного оптимального начального момента времени содержит этапы, на которых:

выбирают временной поддиапазон, который включен в данный временной диапазон, имеет меньшую протяженность, чем протяженность данного временного диапазона, и сцентрирован на идентифицированном оптимальном начальном моменте времени.

Кроме того, выбор поддиапазона долготы на основании данного диапазона долготы и идентифицированного оптимального значения долготы содержит этапы, на которых:

выбирают поддиапазон долготы, который включен в данный диапазон долготы, имеет меньшую протяженность, чем протяженность данного диапазона долготы, и сцентрирован на идентифицированном оптимальном значении долготы.

Кроме того, выбор поддиапазона возвышения на основании данного диапазона возвышения и идентифицированного второго значения возвышения содержит этапы, на которых:

выбирают поддиапазон возвышения, который включен в данный диапазон возвышения, имеет меньшую протяженность, чем протяженность данного диапазона возвышения, и сцентрирован на идентифицированном оптимальном значении возвышения.

Удобно, чтобы способ согласно настоящему изобретению дополнительно содержал:

- если траектория, определенная на основании физико-математической модели, рассматриваемых вторых начальных моментов времени, рассматриваемых вторых значений долготы и рассматриваемых вторых значений возвышения, не отвечает начальным граничным условиям и конечным граничным условиям в пределах предварительно заданного допуска, повторение этапов, на которых

выбирают новый временной поддиапазон на основании предварительно выбранного временного поддиапазона и предварительно идентифицированного оптимального начального момента времени,

выбирают новый поддиапазон долготы на основании предварительно выбранного поддиапазона долготы и предварительно идентифицированного оптимального значения долготы,

выбирают новый поддиапазон возвышения на основании предварительно выбранного поддиапазона возвышения и предварительно идентифицированного оптимального значения возвышения,

рассматривают новые начальные моменты времени, включенные в выбранный новый временной поддиапазон, новые значения долготы конкретного угла долготы, включенные в выбранный новый поддиапазон долготы, и новые значения возвышения конкретного угла возвышения, включенные в выбранный новый поддиапазон возвышения, и

определяют траекторию перемещения космического летательного аппарата на основании физико-математической модели, рассматриваемых новых начальных моментов времени, рассматриваемых новых значений долготы и рассматриваемых новых значений возвышения;

и этап, на котором

- останавливают повторение, если траектория, определенная на основании физико-математической модели, рассматриваемых новых начальных моментов времени, рассматриваемых новых значений долготы и рассматриваемых новых значений возвышения, отвечает начальным граничным условиям и конечным граничным условиям в пределах предварительно заданного допуска.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Для лучшего понимания настоящего изобретения предпочтительные варианты осуществления, призванные служить исключительно примером, но не ограничением, будут описаны со ссылкой на прилагаемые чертежи (выполненные не в масштабе), в которых:

- фиг. 1 демонстрирует макроскопический тренд расширенной функции стоимости, подлежащей минимизации для решения двухточечной краевой задачи;

- фиг. 2 демонстрирует микроскопический тренд расширенной функции стоимости, показанной фиг. 1;

- фиг. 3 демонстрирует логическую блок-схему способа определения оптимальных траекторий перемещения космических летательных аппаратов согласно предпочтительному варианту осуществления настоящего изобретения;

- фиг. 4 демонстрирует первую сетку поиска, построенную для определения оптимальной траектории перемещения Земля-Марс согласно способу, показанному на фиг. 3;

- фиг. 5 демонстрирует вторую сетку поиска, построенную для определения оптимальной траектории перемещения Земля-Марс согласно способу, показанному на фиг. 3;

- фиг. 6 демонстрирует вторую сетку поиска, показанную на фиг. 5, совместно с третьей сеткой поиска, построенной для определения оптимальной траектории перемещения Земля-Марс согласно способу, показанному на фиг. 3; и

- фиг. 7 демонстрирует оптимальную траекторию перемещения Земля-Марс, определенную согласно способу, показанному на фиг. 3.

ПОДРОБНОЕ ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ

Нижеследующее рассмотрение представлено для того, чтобы специалист в данной области техники мог применять и использовать изобретение. Специалисты в данной области техники могут предложить различные модификации вариантов осуществления, не выходя за рамки заявленного объема настоящего изобретения. Таким образом, настоящее изобретение не предусматривает ограничение представленными вариантами осуществления, но должно соответствовать широчайшему объему, согласующемуся с принципами и признаками, раскрытыми в данном документе и заданными в прилагаемой формуле изобретения.

Кроме того, настоящее изобретение реализовано посредством программы программного обеспечения, загружаемой в память электронного процессора и содержащей участки программного кода для реализации, когда программа программного обеспечения выполняется электронным процессором, способа определения оптимальных траекторий перемещения космических летательных аппаратов, описанного далее.

Настоящее изобретение относится к адаптивному способу с множественной пристрелкой, т.е. алгоритму для решения так называемой "двухточечной краевой задачи", применяемой к траекториям перемещения космических летательных аппаратов. Такой способ, с учетом всех предыдущих усилий для решения задач, касающихся оптимизации пространственной траектории, позволяет вычислять направление тяги, необходимое для согласования с граничными условиями, путем минимизации данного функционала стоимости, согласно данной силовой установке.

Заявитель обратил внимание на то, что вышеописанная расширенная функция стоимости J ˜ имеет форму, которая не требует алгоритма поиска ни на основании оценивания градиента, типичного для прямых способов, ни на основании разложения в ряд функционала стоимости, как в прямых способах, применяемых в вариационном исчислении.

Алгоритм согласно настоящему изобретению по-новом