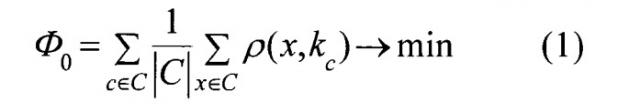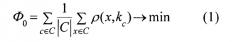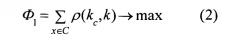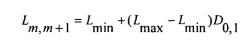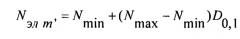Способ моделирования сетей связи

Способ моделирования сетей связи

Иллюстрации

Показать все

Реферат

Изобретение относится к средствам моделирования сетей связи и может быть применено для моделирования топологических неоднородностей сетей связи, инвариантных заданному фрагменту, с учетом физико-географических свойств местности, в целях научных исследований сетей, прогнозирования их развития.

Развитие технического прогресса ведет к увеличению объема и разнообразия информационных потоков, передаваемых по информационным телекоммуникационным сетям. В результате непрерывно расширяются существующие информационные сети, а по мере появления новых видов информации, новых технологий передачи информации создаются новые.

Необходимо отметить, что если раньше единая сеть электросвязи (ЕСЭ) проектировалась и строилась по единому замыслу, который был заложен в долгосрочную программу формирования системы связи страны (регионов), то сейчас на рынок вышло огромное количество операторов связи, каждый из которых в процессе эксплуатации сети связи модернизирует и преобразовывает существующую структуру единой сети электросвязи в части касающейся.

Вследствие этого особенностями современных информационно-телекоммуникационных сетей являются:

- большое число оконечных пунктов и узлов связи и их неоднородность;

- длительность существования с постепенным наращиванием емкостей и расширением предоставляемых услуг;

- большое разнообразие требований к доставке различных сообщений;

- неоднородность пропускных способностей линий (каналов);

- территориальная неоднородность и неоднородность тяготения между отдельными оконечными пунктами. [Давыдов Г.Б., Рогинский В.Н. «Сети электросвязи». - М.: Связь, 1977. - 366 с. с ил.]

Информационно-телекоммуникационные системы относятся к классу больших систем, этапы проектирования, внедрения, эксплуатации и эволюции которых в настоящее время невозможны без использования различных видов моделирования. [Советов Б.Я., Яковлев С.А. «Моделирование систем». - М.: Высшая школа, 2009, - 343 с., Шелухин О.И., Тенякшев A.M., Осин А.В. «Моделирование информационных систем». Учебное пособие. - М.: Радиотехника, 2005. - 368 с.: ил.]

В целях научных исследований существующих информационно-телекоммуникационных сетей и прогнозирования их развития, вследствие их структурной сложности, нерегулярности и неоднородности, становится актуальной разработка способов моделирования фрагментов сетей связи, инвариантных имеющимся.

Инвариантность (от лат. invarians, род. п. invariantis - неизменяющийся) - неизменность какой-либо величины по отношению к некоторым преобразованиям. [Физический энциклопедический словарь. - М.: Советская энциклопедия. Под редакцией А.М. Прохорова. 1983.]

Неоднородность - 1) неравномерность свойств; 2) разрывность; 3) наличие разнородных элементов. [Русско-английский физический словарь. 2013.]

Под топологической структурой будем понимать взаимное расположение элементов сети связи на местности. (Топология - наука, учение о местностях. [Словарь иностранных слов, вошедших в состав русского языка. - Чудинов А.Н., 1910.])

В настоящее время существует два способа моделирования топологической структуры сетей:

- детерминированный (координаты пунктов (узлов) строго заданы) [Давыдов Г.Б., Рогинский В.Н. «Сети электросвязи». - М.: Связь, 1977. - 366 с. с ил.], что достаточно сложно в условиях сбора данных от большого количества региональных операторов связи (например, в Калининградской области на 2010 г. зарегистрировано 439 операторов связи) [Постановление Правительства Калининградской области от 02.08.2012 № «Об утверждении Стратегии социально-экономического развития Калининградской области на период до 2020 года». [Электронный ресурс]. URL: http://www.gosbook.ru/node/67613 (Дата обращения 14.10.2013 г.);

- статистический (координаты пунктов (узлов) заданы распределениями случайных величин) [Коршун В.Г., Макаров М.И. «Математическое обеспечение автоматизированной системы экспресс-анализа и синтеза сетей передачи данных. Учебное пособие. - Спб.: ВАС, 2007. - 128 с.], результаты моделирования которого вызывают сложность при применении на практике.

Так, известен способ моделирования сети связи [изобретение «Способ моделирования сети связи» RU 2476930 G06N 99/00, H04W 16/22, H04L 12/26, опубликованное 27.02.2013, бюл. №6], обеспечивающий возможность моделирования с учетом перемещения абонентов сети связи и вероятности смены узлов сети связи, обслуживающих данных абонентов. Начальная топология и структура сети в данном способе задаются по случайному закону.

Известен способ моделирования сети связи (изобретение «Способ моделирования сетей связи» RU 2379750 C1, G06F 11/22, H04W, опубликованное 20.01.2010, бюл. №2), заключающийся в возможности имитации перемещения элементов и абонентов СС, где функционирует СС и находятся абоненты СС, моделирования изменения топологии СС и изменения емкости каналов (линий) СС.

Недостатком перечисленных выше способов является то, что при моделировании сети связи не учитываются физико-географические условия района (области, недоступные для связи), а также топологические неоднородности, возникающие в процессе развития сети связи, что снижает адекватность моделирования.

Наиболее близким по технической сущности к заявленному способу является способ моделирования (изобретение “Способ моделирования разнородных сетей связи” RU 2481629 C1, G06F 17/50, G06F 17/10, опубликованное 10.05.2013, бюл. №13). Способ заключается в том, что задают исходные данные, формируют в каждом из статистических экспериментов граф вероятностной сети, в котором существует или отсутствует маршрут в заданных информационных направлениях, имитируют перемещение абонентов, генерируют начальную топологию и структуру разнородных сетей, при этом для каждой разнородной сети связи осуществляется генерация координат размещения ее элементов, формируют матрицу информационных направлений между узлами разнородных сетей связи, имитируют соединение узла сети с другим узлом сети, фиксируют пути успешного функционирования для каждого информационного направления, генерируют значения пропускной способности и показателя живучести для сформированной линии привязки между узлами, рассчитывают вероятность наличия маршрута между абонентами.

Генерация координат разнородных сетей в данном способе осуществляется с помощью датчиков случайных величин с различными законами распределения и параметрами.

Недостатком данного способа является отсутствие данных, позволяющих осуществить адекватный выбор закона распределения при генерации координат элементов сети связи, а также то, что физико-географические условия района и топологические неоднородности, возникающие в процессе развития сети связи, не учитываются, что снижает достоверность и адекватность моделирования.

Техническим результатом изобретения является повышение достоверности и адекватности моделирования, а также возможность моделирования фрагментов сетей связи, инвариантных имеющимся, с учетом физико-географических условий местности и топологических неоднородностей, возникших в процессе развития сети, за счет того, что исходные данные для моделирования формируют исходя из топологической структуры реальной сети, затем моделируют расположение неоднородностей в заданном фрагменте и расположение элементов в каждой неоднородности.

Технический результат достигается тем, что в известном способе моделирования сетей связи, заключающемся в том, что задают исходные данные, формируют в каждом из статистических экспериментов граф вероятностной сети, в котором существует или отсутствует маршрут в заданных информационных направлениях, имитируют перемещение абонентов, генерируют начальную топологию и структуру разнородных сетей, при этом для каждой разнородной сети связи осуществляется генерация координат размещения ее элементов, формируют матрицу информационных направлений между узлами разнородных сетей связи, имитируют соединение узла сети с другим узлом сети, фиксируют пути успешного функционирования для каждого информационного направления, генерируют значения пропускной способности и показателя живучести для сформированной линии привязки между узлами, рассчитывают вероятность наличия маршрута между абонентами, для формирования необходимых исходных данных дополнительно задают площадь реального фрагмента сети связи произвольной формы выбранного региона, радиусы площадей неоднородностей Rmin, Rmax, шаг ΔR, присваивают номера от 1 до I элементам сети связи заданного фрагмента, фиксируют географические координаты (Xi, Yi) элементов сети связи заданного фрагмента, фиксируют географические области, недоступные для связи в заданном фрагменте, задают радиус площади неоднородности Rs=Rmin, совмещают центр неоднородности с координатами i-го элемента сети связи (Xi, Yi), где i=1, 2, …, I, вычисляют расстояние от центра неоднородности до всех остальных элементов сети связи r_ij, фиксируют координаты элементов сети связи, до которых расстояние меньше заданного радиуса неоднородности r_ij<R_s, вычисляют координаты центра тяжести для зафиксированных элементов, вычисляют расстояния от вычисленного центра тяжести до остальных элементов сети связи, фиксируют координаты точек, для которых расстояние k_ci<R_S, проверяют, совпадают ли координаты центров тяжести, если координаты центров тяжести совпадают, то причисляют элементы, для которых k_ci<R_S, к неоднородности T_m, запоминают результат, исключают элементы, причисленные к неоднородности T_m, из множества , проверяют, все ли элементы причислены к неоднородностям, если нет, то переходят к формированию следующей неоднородности T_m+1, выбирают элемент из оставшегося множества, совмещают центр неоднородности с координатами выбранного элемента и повторяют действия по формированию неоднородности Т_m, пока все элементы не будут причислены к неоднородностям, вычисляют по определенному правилу функционалы качества Ф_0i, Ф_1i, запоминают значение функционалов качества, радиус неоднородности, количество неоднородностей m и их состав, затем повторяют действия по формированию неоднородностей, начиная поочередно со всех элементов сети связи от i+1-го до I-го, далее вычисляют Rs=Rs+ΔR, сравнивают вычисленное значение радиуса площади неоднородности с заданным максимальным значением, если Rs<Rmax, то повторяют действия по формированию неоднородностей с вычисленным значением радиуса Rs, если Rs>Rmax, то выбирают вариант с наилучшими функционалами качества, фиксируют радиус площади неоднородности Rs, количество m и состав неоднородностей для выбранного варианта, стирают невыбранные запомненные ранее результаты итераций, подсчитывают количество элементов N в каждой неоднородности, фиксируют минимальное N_min и максимальное N_max количество элементов в неоднородностях, вычисляют расстояния L_mk между центрами неоднородностей, фиксируют минимальное, максимальное L_min, L_max, после этого переходят к моделированию расположения неоднородностей в заданном фрагменте, для чего формируют фрагмент заданной площади, генерируют с помощью датчика случайных чисел с обоснованным законом распределения координаты центра первой неоднородности, запоминают координаты центра неоднородности, формируют неоднородность радиусом Rs с центром в полученной точке, присваивают ей номер m′, вычисляют координаты центра следующей неоднородности m′+1 по заданному правилу, проверяют, принадлежат ли координаты выделенному фрагменту, если не принадлежат, то возвращаются к вычислению центра неоднородностей, если принадлежат, то запоминают координаты центра m′+1-й неоднородности, формируют неоднородность радиусом Rs с центром в полученной точке, присваивают ей номер m′+1, проверяют, все ли m неоднородностей сформированы, если не сформированы, то повторяют действия по вычислению центра и формированию неоднородностей, если все неоднородности сформированы, то приступают к моделированию расположения элементов в каждой неоднородности, для чего выбирают сформированную топологическую неоднородность с номером m′=1, вычисляют количество элементов в неоднородности по заданному правилу, генерируют с помощью датчика случайных чисел с обоснованным законом распределения координаты n-го элемента, проверяют, не попали ли координаты в область, недоступную для связи, если попали, то генерируют координаты n-го элемента заново, если не попали, то запоминают координаты n-го элемента, проверяют, расположение всех ли элементов смоделировано, если смоделировано расположение не всех элементов, то вычисляют координаты n+1-го элемента при условии, что координаты центра тяжести не должны измениться, проверяют, не попали ли координаты n+1-го элемента в область, недоступную для связи, если попали, то генерируют координаты n+1-го элемента с вышеописанной проверкой, если не попали, то запоминают координаты n+1-го элемента, проверяют, расположение всех ли элементов смоделировано, если нет, то повторяют действия, пока не будет смоделировано расположение всех Nэл в данной неоднородности, если смоделировано расположение всех Nэл в данной неоднородности, то проверяют, смоделировано ли расположение элементов во всех неоднородностях, если нет, то повторяют действия по перечисленной совокупности действий моделирования от m′+1-й неоднородности до m.

Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностями признаков, тождественным всем признакам заявленного способа, отсутствуют. Следовательно, заявленное изобретение соответствует условию патентоспособности “новизна”.

Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличительными от прототипов признаками заявленного изобретения, показали, что они не следуют явным образом из уровня техники. Из определенного заявителем уровня техники не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности “изобретательский уровень”.

Заявленный способ поясняется чертежами, на которых показаны:

фиг.1 - алгоритм способа моделирования топологических неоднородностей сетей связи, инвариантных заданному фрагменту с учетом физико-географических условий местности;

фиг.2 - алгоритм формирования исходных данных для моделирования;

фиг.3 - алгоритм моделирования расположения неоднородностей в заданном фрагменте;

фиг.4 - графическое представление моделирования расположения неоднородностей в заданном фрагменте;

фиг.5 - алгоритм моделирования расположения элементов в каждой неоднородности;

фиг.6 - графическое представление моделирования расположения элементов в каждой неоднородности.

Заявленный способ реализован в виде алгоритма моделирования, представленного на фиг.1.

В блоке 1 осуществляется формирование исходных данных для моделирования, а именно: количество неоднородностей m, минимальное и максимальное количество элементов в неоднородностях Nmin, Nmax, минимальное и максимальное расстояние между центрами неоднородностей Lmin, Lmax, радиус неоднородности Rs.

В блоке 2 осуществляется моделирование расположения неоднородностей в заданном фрагменте.

В блоке 3 осуществляется моделирование элементов в каждой неоднородности.

Формирование исходных данных для моделирования реализовано в виде алгоритма, представленного на фиг.2:

В блоке 1 вводят исходные данные, а именно: площадь реального фрагмента сети связи выбранного региона, радиусы неоднородностей Rmin, Rmax, шаг изменения радиуса ΔR.

В блоке 2 присваивают номера от 1 до 7 элементами сети связи заданного фрагмента.

В блоке 3 фиксируют географические координаты (Xi, Yi) элементов сети связи заданного фрагмента.

В блоке 4 фиксируют географические области, недоступные для связи в заданном фрагменте.

В блоках 5-28 выделяют неоднородности сети связи заданного фрагмента путем применения адаптированного алгоритма кластеризации FOREL.

Согласно [Загоруйко Н.Г. «Методы распознавания и их применение». - М.: Советское радио. 1972 - 208 с., Загоруйко Н.Г. Прикладные методы анализа данных и знаний. [Электронный ресурс]. URL:http://www.alingva.ru/index.php/2010-05-24-19-29-23/6-2010-05-25-18-58-50 (Дата обращения 24.03.2013 г.)] алгоритмы данного класса дают быстрые и простые решения. Доказана сходимость алгоритма за конечное число шагов. Кластеры, получаемые этим алгоритмом, имеют сферическую форму. Их количество зависит от радиуса сфер. Варьируя параметр R, можно получать кластеризации различной степени детальности, а также описывать фрагменты заданного региона произвольной геометрической формы.

Поскольку начальное положение центров выбирается случайным образом, кластеризации будут довольно сильно отличаться. Результат будет зависеть от того, с какой первой точки был начат процесс.

Для устранения данного недостатка в алгоритме предусмотрено начало итераций с каждого элемента сети заданного фрагмента. Окончательно выбирается та кластеризация, которая доставляет наилучшее значение заданному функционалу качества.

Разновидности функционалов качества кластеризации описаны, например, в [Загоруйко Н.Г. «Методы распознавания и их применение». - М.: Советское радио. 1972 - 208 с.]

Так как алгоритм вычисляет центры кластеров, то вычислительно более эффективными можно определить следующие функционалы [Воронцов К.В. Лекции по алгоритмам кластеризации. [Электронный ресурс]. URL:http://www.ccas.ru/voron/download/Clustering.pdf (Дата обращения 24.03.2013 г.), Бериков В.Б., Лбов Г.С. «Современные тенденции в кластерном анализе». // Всероссийский конкурсный отбор обзорно-аналитических статей по приоритетному направлению «Информационно-телекоммуникационные системы», 2008. - 26 с., Николенко С. Алгоритмы кластеризации. [Электронный ресурс]. URL:http://logic.pdmi.ras.ru/~sergey/teaching/m1/11-cluster.pdf (Дата обращения 24.03.2013 г.]:

1. Сумма средних внутрикластерных расстояний должна быть как можно меньше:

где k_c - центр кластера C.

2. Сумма межкластерных расстояний должна быть как можно больше:

где k - центр тяжести всей выборки.

Выделение кластеров (неоднородностей) сети связи заданного фрагмента производится следующим образом:

В блоке 5 задают радиус кластера (неоднородности) Rs=Rmin.

Затем приступают к выделению первого кластера (неоднородности).

В блоке 7 совмещают центр кластера (неоднородности) с координатами первого элемента сети связи заданного фрагмента.

В блоке 8 вычисляют расстояния от центра кластера (неоднородности) до всех остальных элементов сети связи.

В блоке 9 сравнивают вычисленные расстояния с заданным радиусом кластера (неоднородности).

В блоке 10 фиксируют координаты элементов сети связи, для которых r_ij<R. Элементы, для которых r_ij>R, на данном этапе не рассматриваются.

В блоке 11 вычисляют координаты центра тяжести для зафиксированных точек.

Примеры вычисления координат центра тяжести плоских фигур приведены в [Виленкин Н.Я., Куницкая Е.С., Мордкович А.Г. «Математический анализ. Интегральное исчисление». - М.: «Просвещение», 1979. - 176 с.]

В блоке 12 вычисляют расстояния от центра тяжести до всех остальных элементов сети связи ρ_ci.

В блоке 13 сравнивают вычисленные расстояния с заданным радиусом кластера (неоднородности).

В блоке 14 фиксируют координаты точек, для которых расстояние меньше заданного радиуса кластера (неоднородности) ρ_ci<Rs.

В блоке 15 вычисляют координаты центра тяжести для зафиксированных точек.

В блоке 16 проверяют, совпали ли координаты центров тяжести, вычисленных в блоках 11 и 15. Если нет, то повторяют шаги, выполняемые в блоках 12-15, пока координаты центров тяжести не совпадут.

В блоке 17 причисляют элементы сети связи, расстояние до которых меньше заданного радиуса, к первому кластеру (неоднородности) С₁.

В блоке 18 запоминают результат.

В блоке 19 исключают элементы сети связи, причисленные к первому кластеру (неоднородности), из множества .

В блоке 21 проверяют, все ли элементы сети связи причислены к кластерам (неоднородностям). Если нет, то приступают к выделению второго кластера (неоднородности), выбирая начальную точку в блоке 22 из оставшегося множества и повторяя шаги, выполняемые в блоках 7-20. И так далее, пока все элементы не будут причислены к С_m кластерам (неоднородностям).

В блоке 23 вычисляют значения функционалов качества Ф₀ и Ф₁ по правилам (1) и (2).

В блоке 24 запоминают значения функционалов качества, радиус кластера (неоднородности) Rs, количество кластеров (неоднородностей) m и их состав.

Повторяют вышеперечисленные действия (блоки 7-26), начиная кластеризацию со второго элемента (i=2), потом с третьего (i=3)… до I-го (i=I).

В блоке 27 увеличивают значение заданного радиуса кластера (неоднородности) на величину ΔR.

В блоке 28 проверяют, не достигло ли значение радиуса неоднородности максимального заданного R_max. Если нет, то повторяют действия, производимые в блоках 5-28 для вычисленного радиуса неоднородности. Если увеличенное значение радиуса кластера (неоднородности) R_S достигло максимального заданного значения R_max, то в в блоке 29 выбирают вариант с наилучшими функционалами качества Ф₀ и Ф₁ при условии

,

фиксируют радиус кластера (неоднородности) R_S, количество m и состав кластеров (неоднородностей) для данного варианта.

В блоке 30 стирают остальные ранее запомненные результаты итераций.

В блоке 31 подсчитывают количество элементов в каждом кластере (неоднородности). Фиксируют минимальное Nmin, максимальное Nmax количество элементов в кластерах (неоднородностях).

В блоке 32 вычисляют расстояния Lmk между центрами кластеров (неоднородностей). Фиксируют минимальное Lmin, максимальное Lmax расстояния между центрами кластеров (неоднородностей).

В блоке 33 выводят все необходимые для дальнейшего моделирования данные: количество неоднородностей m, минимальное, максимальное количество элементов в неоднородностях Nmin, Nmax, минимальное, максимальное расстояние между центрами неоднородностей Lmin, Lmax, радиус площади неоднородности Rs.

Моделирование расположения неоднородностей в заданном фрагменте реализовано в виде алгоритма, представленного на фиг.3, 4:

В блоке 1 вводят данные, полученные при помощи предыдущего алгоритма, а именно количество неоднородностей m, минимальное, максимальное количество элементов в неоднородностях Nmin, Nmax, минимальное, максимальное расстояние между центрами неоднородностей Lmin, Lmax, радиус неоднородности R_S, а также площадь (границы) заданного фрагмента.

В блоке 2 формируют фрагмент заданной площади.

В блоке 3 устанавливают в единицу счетчик, определяющий номер формируемой неоднородности.

Далее в блоке 4 генерируют с помощью ДСЧ с обоснованным законом распределения координаты центра первой неоднородности.

Методы генерации последовательности случайных чисел по заданному закону распределения случайных величин описаны в [Дональд Кнут. Искусство программирования, том 2. Получисленные алгоритмы - 3-е изд. - М: “Вильямс”, 2007. - c.11-165].

В блоке 5 запоминают координаты центра первой неоднородности.

В блоке 6 формируют площадь неоднородности радиусом Rs с центром в полученной точке.

В блоке 7 присваивают ей номер m′.

Далее переходят к вычислению координат центра m′+1-й топологической неоднородности по правилу треугольника.

Для этого определяют расстояние между центрами m′-й и m′+1-й неоднородностей по правилу:

,

где D_0,1 - случайное число, распределенное в интервале (0,1), получаемое с помощью датчика случайных чисел.

Угол отклонения от оси ОХ вычисляется следующим образом:

α=360*D_0,1

Тогда координаты центра m′+1-й топологической неоднородности могут быть вычислены с помощью соотношений:

,

В блоке 10 проверяют, принадлежат ли координаты заданному фрагменту. Если нет, то повторяют действия, производимые в блоке 9.

Если координаты принадлежат заданному фрагменту, то в блоке 11 запоминают их.

В блоке 12 формируют неоднородность радиусом Rs с центром в полученной точке.

В блоке 13 присваивают ей номер.

В блоке 14 проверяют, все ли m неоднородностей сформированы. Если нет, то повторяют действия, выполняемые в блоках 8-14. Если все m неоднородностей сформированы, то приступают к моделированию расположения элементов в каждой из топологических неоднородностей.

Моделирование расположения топологических неоднородностей реализовано в виде алгоритма, представленного на фиг.5, 6:

В блоке 1 вводят исходные данные: сформированные площади неоднородностей, количество неоднородностей m, минимальное, максимальное количество элементов в неоднородностях Nmin, Nmax.

В блоке 2 устанавливают в единицу счетчик, определяющий номер неоднородности m′, в которой моделируем расположение элементов.

В блоке 3 выбирают сформированную топологическую неоднородность m′.

В блоке 4 вычисляют количество элементов сети связи для данной неоднородности по правилу:

,

где D_0,1 - случайное число, распределенное в интервале (0, 1), получаемое с помощью датчика случайных чисел.

В блоке 5 устанавливают в единицу счетчик, определяющий номер элемента сети связи n в неоднородности m′.

В блоке 6 генерируют с помощью ДСЧ с обоснованным законом распределения координаты первого элемента сети связи.

В блоке 7 проверяют, не попали ли сгенерированные координаты в область, недоступную для связи. Если координаты попали в область, недоступную для связи, то их генерируют заново.

Если координаты не попали в область, недоступную для связи, то в блоке 8 запоминают координаты n-го элемента.

В блоке 9 проверяют, координаты всех ли элементов N_эл смоделированы. Если нет, то в блоке 13 вычисляют координаты n+1-го элемента при условии, что координаты центра тяжести не должны измениться.

В блоке 14 проверяют, не попали ли сгенерированные координаты в область, недоступную для связи. Если координаты попали в область, недоступную для связи, то повторяют действия, выполняемые в блоках 6-14.

Если координаты не попали в область, недоступную для связи, то в блоке 15 запоминают координаты n-го элемента.

В блоке 17 проверяют, координаты всех ли элементов N_эл смоделированы. Если нет, то повторяют действия, выполняемые в блоках 5-17.

Если все координаты всех элементов неоднородности N_эл сформированы, то переходят к моделированию расположения элементов сети связи в следующей неоднородности, для чего в блоке 11 увеличивают счетчик, определяющий номер неоднородности на 1.

В блоке 12 проверяют, во всех ли m неоднородностях смоделировано расположение элементов. Если нет, то повторяют действия, выполняемые для моделирования элементов первой неоднородности.

Если расположение элементов смоделировано во всех неоднородностях, то моделирование топологических неоднородностей, инвариантных заданному фрагменту, считают завершенным.

Таким образом, за счет формирования исходных данных исходя из учета топологической структуры реальной сети, учета физико-географических условий местности и топологических неоднородностей, возникших в процессе развития сети, повышается достоверность и адекватность моделирования, а также появляется возможность моделирования фрагментов сетей связи, инвариантных имеющимся, что и определяет достижение технического результата.

Способ моделирования сетей связи, заключающийся в том, что задают исходные данные, формируют в каждом из статистических экспериментов граф вероятностной сети, в котором существует или отсутствует маршрут в заданных информационных направлениях, имитируют перемещение абонентов, генерируют начальную топологию и структуру разнородных сетей, при этом для каждой разнородной сети связи осуществляется генерация координат размещения ее элементов, формируют матрицу информационных направлений между узлами разнородных сетей связи, имитируют соединение узла сети с другим узлом сети, фиксируют пути успешного функционирования для каждого информационного направления, генерируют значения пропускной способности и показателя живучести для сформированной линии привязки между узлами, рассчитывают вероятность наличия маршрута между абонентами, отличающийся тем, что для формирования необходимых исходных данных дополнительно задают площадь реального фрагмента сети связи произвольной формы выбранного региона, радиусы площадей неоднородностей Rmin, Rmax, шаг ΔR, присваивают номера от 1 до I элементам сети связи заданного фрагмента, фиксируют географические координаты (Xi, Yi) элементов сети связи заданного фрагмента, фиксируют географические области, недоступные для связи в заданном фрагменте, задают радиус площади неоднородности Rs=Rmin, совмещают центр неоднородности с координатами i-го элемента сети связи (Xi, Yi), где i=1,2,…,I, вычисляют расстояние от центра неоднородности до всех остальных элементов сети связи r_ij, фиксируют координаты элементов сети связи, до которых расстояние меньше заданного радиуса неоднородности r_ij<R_S, вычисляют координаты центра тяжести для зафиксированных элементов, вычисляют расстояния от вычисленного центра тяжести до остальных элементов сети связи, фиксируют координаты точек, для которых расстояние k_ci<R_s, проверяют, совпадают ли координаты центров тяжести, если координаты центров тяжести совпадают, то причисляют элементы, для которых k_ci<R_s, к неоднородности T_m, запоминают результат, исключают элементы, причисленные к неоднородности T_m из множества 1, I ¯ , проверяют, все ли элементы причислены к неоднородностям, если нет, то переходят к формированию следующей неоднородности T_m+₁, выбирают элемент из оставшегося множества, совмещают центр неоднородности с координатами выбранного элемента и повторяют действия по формированию неоднородности Т_m, пока все элементы не будут причислены к неоднородностям, вычисляют по определенному правилу функционалы качества Ф_0i, Ф_1i, запоминают значение функционалов качества, радиус неоднородности, количество неоднородностей m и их состав, затем повторяют действия по формированию неоднородностей, начиная поочередно со всех элементов сети связи от i+1-го до I-го, далее вычисляют Rs=Rs+ΔR, сравнивают вычисленное значение радиуса площади неоднородности с заданным максимальным значением, если Rs<Rmax, то повторяют действия по формированию неоднородностей с вычисленным значением радиуса Rs, если Rs>Rmax, то выбирают вариант с наилучшими функционалами качества, фиксируют радиус площади неоднородности Rs, количество m и состав неоднородностей для выбранного варианта, стирают невыбранные запомненные ранее результаты итераций, подсчитывают количество элементов N в каждой неоднородности, фиксируют минимальное N_min и максимальное N_max количество элементов в неоднородностях, вычисляют расстояния L_mk между центрами неоднородностей, фиксируют минимальное, максимальное L_min, L_max, после этого переходят к моделированию расположения неоднородностей в заданном фрагменте, для чего формируют фрагмент заданной площади, генерируют с помощью датчика случайных чисел с обоснованным законом распределения координаты центра первой неоднородности, запоминают координаты центра неоднородности, формируют неоднородность радиусом Rs с центром в полученной точке, присваивают ей номер m′, вычисляют координаты центра следующей неоднородности m′+1 по заданному правилу, проверяют, принадлежат ли координаты выделенному фрагменту, если не принадлежат, то возвращаются к вычислению центра неоднородностей, если принадлежат, то запоминают координаты центра m′+1-й неоднородности, формируют неоднородность радиусом Rs с центром в полученной точке, присваивают ей номер m′+1, проверяют, все ли m неоднородностей сформированы, если не сформированы, то повторяют действия по вычислению центра и формированию неоднородностей, если все неоднородности сформированы, то приступают к моделированию расположения элементов в каждой неоднородности, для чего выбирают сформированную топологическую неоднородность с номером m′=1, вычисляют количество элементов в неоднородности по заданному правилу, генерируют с помощью датчика случайных чисел с обоснованным законом распределения координаты n-го элемента, проверяют, не попали ли координаты в область, недоступную для связи, если попали, то генерируют координаты n-го элемента заново, если не попали, то запоминают координаты n-го элемента, проверяют, расположение всех ли элементов смоделировано, если смоделировано расположение не всех элементов, то вычисляют координаты n+1-го элемента при условии, что координаты центра тяжести не должны измениться, проверяют, не попали ли координаты n+1-го элемента в область, недоступную для связи, если попали, то генерируют координаты n+1-го элемента с вышеописанной проверкой, если не попали, то запоминают координаты n+1-го элемента, проверяют, расположение всех ли элементов смоделировано, если нет, то повторяют действия, пока не будет смоделировано расположение всех Nэл в данной неоднородности, если смоделировано расположение всех Nэл в данной неоднородности, то проверяют, смоделировано ли расположение элементов во всех неоднородностях, если нет, то повторяют действия по перечисленной совокупности действий моделирования от m′+1-й неоднородности до m.