Генератор коррелированных случайных сигналов

Генератор коррелированных случайных сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области создания устройств для генерирования широкополосных случайных стационарных сигналов с заданными собственными и взаимными спектральными плотностями мощности и может быть использовано в приборостроении, машиностроении, вычислительной технике для создания, в частности, многоканальных автоматических систем, в испытаниях на вибростойкость к воздействиям случайной вибрации и т.д.

Известно («Автоматическое управление вибрационными испытаниями», Библиотека по автоматике выпуск 579, Москва, Энергия, 1978 г.) устройство, генерирующее одномерный случайный стационарный сигнал с заданной спектральной плотностью, состоящее из стандартного однопроцессорного компьютера, программного обеспечения для формирования по заданной спектральной плотности случайного сигнала в форме разложения Райса-Пирсона со случайной на каждой гармонике фазой, равномерно распределенной в диапазоне [-π, π], и выполнения процедуры обратного быстрого преобразования Фурье (ОБПФ), модуля цифро-аналогового преобразователя для перевода сформированных цифровых процессов в аналоговые сигналы генератора.

Сформированные таким способом случайные сигналы являются независимыми, что в некоторых случаях является недостатком.

Предлагаемым изобретением решается задача генерирования двух случайных сигналов x(f) и y(f) с заданной функцией когерентности γ_xy(f).

Для достижения названного технического результата предлагается генератор коррелированных случайных сигналов x(t) и y(t), включающий стандартный однопроцессорный компьютер, программное обеспечение для формирования по заданным спектральным плотностям S_x(f) и S_y(f) случайных сигналов в форме разложения Райса-Пирсона со случайными на каждой гармонике f_i фазами Θ_i, и Ω_i, определяемыми методом случайной выборки случайной величины, одна из которых - Θ_i, для сигнала x(t) равномерно распределена в диапазоне [-π, π], а другая - Ω_i для второго сигнала y(t), определяется как сумма Ω_i=Θ_i +Δφ_i случайной величины Θ_i и случайной величины Δφ_i, равномерно распределенной в диапазоне [-φ_i, φ_i], границы которого определяются через взаимную спектральную плотность S_xy(f) случайных сигналов x(t) и y(t) из решения уравнения:

sin ϕ i ϕ i = S x y ( f i ) S x ( f i ) ⋅ S y ( f i )

с последующим выполнением процедуры ОБПФ, модуля цифро-аналогового преобразователя для перевода сформированных цифровых сигналов в аналоговые сигналы генератора.

Отличительным признаком предлагаемого устройства является формирование по заданным спектральным плотностям S_x(f) и S_y(f) и взаимной спектральной плотности S_xy(f) двух случайных сигналов x(t) и y(t) с заданной функцией когерентности γ_xy(f) путем определения на каждой гармонике f_i случайной фазы Θ_i, одного сигнала x(t) методом случайной выборки случайной величины, равномерно распределенной в диапазоне [-π, π], а случайной фазы Ω_i второго сигнала y(f) как суммы Ω_i=Θ_i +Δφ_i случайной величины Θ_i, равномерно распределенной в диапазоне [-π, π], и случайной величины Δφ_i, равномерно распределенной в диапазоне [-φ_i, φ_i], границы которого определяются через взаимную спектральную плотность S_xy(f) случайных сигналов x(f) и y(t) из решения уравнения:

sin ϕ i ϕ i = S x y ( f i ) S x ( f i ) ⋅ S y ( f i )

Благодаря наличию указанного отличительного признака в совокупности с известными приобретается возможность формирования двух случайных сигналов x(t) и y(t) с заданной функцией когерентности γ_xy(f).

В результате поиска по источникам патентной и научно-технической информации, решений, содержащих аналогичные признаки, не обнаружено.

Таким образом, можно сделать заключение о том, что предложенное устройство неизвестно на уровне техники и, следовательно, соответствует критерию «патентоспособности».

Предложенное устройство может найти применение везде, где возникает необходимость в случайных взаимно коррелированных сигналах с заданным уровнем когерентности, что позволяет сделать вывод о соответствии критерию «Промышленная применимость».

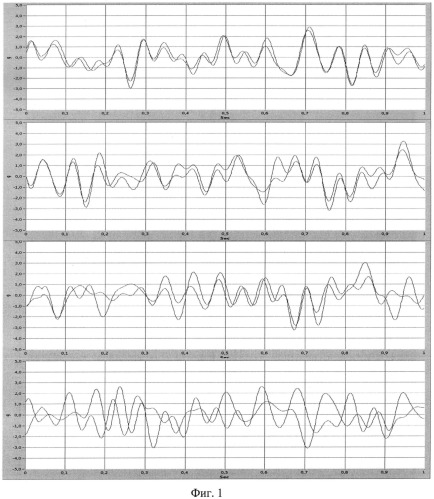
В качестве иллюстрации на фигуре 1 приведены примеры взаимосвязанных процессов (2-20 Гц, белый шум, 1g среднеквадратическое значение) с когерентностью 0,9; 0,7; 0,5 и 0,0 соответственно, полученные предложенным способом.

Генератор коррелированных случайных сигналов x(t) и y(t), включающий стандартный однопроцессорный компьютер, программное обеспечение для формирования по заданным спектральным плотностям S_x(f) и S_y(f) случайных сигналов в форме разложения Райса-Пирсона со случайными на каждой гармонике f_i фазами Θ_i и Ω_i, отличающийся тем, что случайные фазы Θ_i одного сигнала x(f) определяются на каждой гармонике f_i методом случайной выборки случайной величины, равномерно распределенной в диапазоне [-π, π], а случайные фазы Ω_i второго сигнала y(t) определяются на каждой гармонике f_i как сумма Ω_i=Θ_i+Δφ_i случайной величины Θ_i, равномерно распределенной в диапазоне [-π, π], и случайной величины Δφ_i, равномерно распределенной в диапазоне[-φ_i, φ_i], границы которого определяются через взаимную спектральную плотность S_xy(f) случайных сигналов x(t) и y(t) из решения уравнения: sin ϕ i ϕ i = S x y ( f i ) S x ( f i ) ⋅ S y ( f i )