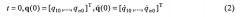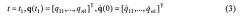Устройство контура фазовой автоподстройки частоты с обратной связью на основе объединенного принципа максимума

Устройство контура фазовой автоподстройки частоты с обратной связью на основе объединенного принципа максимума

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиоавтоматики и может быть использовано в радиотехнических устройствах и системах связи различного назначения для повышения стабильности частот и синхронизации приемной и передающей аппаратуры.

Известны различные модификации устройств контуров фазовой автоподстройки частоты (ФАПЧ) [1]. Все они представляют собой следящую систему автоматического регулирования с одним «входом», одним «выходом» и однопетлевой обратной связью, где объектом регулирования является подстраиваемый генератор. При построении таких систем основное внимание уделяют решению проблемы определения условий устойчивости требуемого режима, а также качественных характеристик процесса его установления. Наиболее близким по технической сущности к заявленному изобретению является устройство фазовой автоподстройки частоты (ФАПЧ) (фиг.1) [1, с.15], где ЭГ - эталонный генератор, УЭ - управляющий элемент, ПГ - подстраиваемый генератор, ФД - фазовый детектор, ФНЧ - фильтр нижних частот.

Однако проектирование мультиагентных систем требует минимизировать время вхождения в синхронизм (время захвата), что сложно обеспечить на основе использования известного устройства, и это определяет его недостаток.

Цель изобретения - уменьшить время захвата в сравнении с устройством ФАПЧ с однозвенным RC-фильтром. Указанный технический результат достигается за счет реализации устройства контура фазовой автоподстройки частоты с обратной связью на основе объединенного принципа максимума [2-5, 7], которое содержит следующие блоки: ЭГ; ПГ; блок формирования arcsin; блок формирования sign; блок формирования модуля; первый, второй, третий, четвертый, пятый, шестой, седьмой блоки формирования произведения; первый и второй блоки формирования суммы, RC-фильтр, интегрирующий масштабный преобразователь, блок формирования производной, форсирующее звено.

При этом в ЭГ, который является входом устройства, формируется значение наблюдаемой величины. Выход ЭГ соединен с первым входом первого блока формирования произведения, выход которого соединен с первым входом первого блока формирования суммы, выход которого соединен с входом RC-фильтра, первый выход которого соединен с входом интегрирующего масштабного преобразователя, выход которого соединен с входом ПГ, первый выход которого соединен со вторым входом первого блока формирования произведения; второй выход ПГ является выходом устройства. Второй выход RC-фильтра соединен с входом форсирующего звена, выход которого соединен с входом блока формирования arcsin, первый выход которого соединен с входом блока формирования производной, первый выход которого соединен с входом блока формирования модуля, выход которого соединен с первым входом второго блока формирования произведения, выход которого соединен с входом четвертого блока формирования произведения, выход которого соединен со вторым входом пятого блока формирования произведения, выход которого соединен с входом шестого блока формирования произведения, выход которого соединен со вторым входом второго блока формирования суммы, выход которого соединен с входом блока формирования sign, выход которого соединен с входом седьмого блока формирования произведения, выход которого соединен со вторым входом первого блока формирования суммы; второй выход блока формирования arcsin соединен с входом третьего блока формирования произведения, выход которого соединен с первым входом пятого блока формирования произведения; третий выход блока формирования arcsin соединен с первым входом второго блока формирования суммы.

Сущность изобретения поясняется чертежами, где на фиг.2 представлено устройство контура фазовой автоподстройки частоты с обратной связью на основе объединенного принципа максимума, которое содержит:

1 - ЭГ;

2 - первый блок формирования произведения;

3 - первый блок формирования суммы;

4 - RC-фильтр;

5 - интегрирующий масштабный преобразователь;

6 - ПГ;

7 - блок формирования arcsin;

8 - блок формирования производной;

9 - блок формирования модуля;

10 - второй блок формирования произведения;

11 - третий блок формирования произведения;

12 - четвертый блок формирования произведения;

13 - пятый блок формирования произведения;

14 - шестой блок формирования произведения;

15 - второй блок формирования суммы;

16 - блок формирования sign;

17 - седьмой блок формирования произведения;

18 - форсирующее звено.

Пояснить работу устройства позволяют следующие математические выкладки.

Рассматривается голономная управляемая динамическая система, интеграл действия которой имеет вид [6]

где T = 1 2 ∑ s , k = 1 n a s k q ˙ s q ˙ k - кинетическая энергия; q=[q₁, …, q_n]^T - вектор обобщенных координат; a _sk - коэффициенты инерции; A = ∫ q ( 0 ) q ( t 1 ) ∑ s = 1 n Q s d q s - работа обобщенных внешних сил; Q = [ Q 1 ( q , q ˙ , u ) , … , Q 1 ( q , q ˙ , u ) ] T - непрерывный по совокупности переменных вектор обобщенных сил; u=[u₁, …, u_m]^T - вектор управления; q(0), q(t) - соответственно начальное и текущее состояние вектора обобщенных координат; n=dim q≥m=dim u, ^T - знак транспонирования, точкой обозначена производная по времени.

Потребуем, чтобы при движении системы из начального состояния

в конечное состояние

под действием управления u выполнялось соотношение, аналогичное принципу Гамильтона-Остроградского для интеграла действия (1)

где знак δ′ - бесконечно малая величина, зависящая от вектора вариаций обобщенных координат, но не являющаяся вариацией величины А [6]

Отметим, что данное требование позволяет утверждать, что справедливы уравнения Лагранжа второго рода, которые для голономной системы можно записать в виде [3]

Пусть задана скалярная непрерывная вместе с частными производными на всей области определения знакопостоянная функция F ( q , q ˙ ) . Сформулируем задачу оптимального уравнения: определить вектор-функции u ( q , q ˙ ) и q(t), доставляющие минимум функционалу

при условиях (2), (3), (4) и ограничении

где G ¯ u - замкнутое множество допустимых управлений в пространстве кусочно-непрерывных на конечном интервале времени [0, t₁] функций.

Рассмотрим расширенный функционал следующего вида:

где λ - множитель Лагранжа. Пусть u ∈ G ¯ u - произвольное допустимое управление. Тогда, если u ~ доставляет минимум функционалу (8), необходимо чтобы его вариация была неотрицательна

δJ≥0

для любых допустимых вариаций δu.

Введем в рассмотрение функцию Ф ( q , q ˙ , u , λ ) :

где V_s=δ′F/δq_s. По физическому смыслу она представляет мощность действительных обобщенных сил Q s = Q s ( q , q ˙ , u ) , явно зависящих от управления u ∈ G ¯ u и фиктивных обобщенных сил V s ( q , q ˙ ) = δ ' F / δ q s , определяемых формой заданного функционала. Функция Ф ( q , q ˙ , u , λ ) , λ∈R непрерывна по совокупности переменных и определена на области

где Ω - некоторая ограниченная в пространстве непрерывных на конечном интервале времени [0, t₁] функций область, которая представляет собой множество решений уравнения (5). Ограниченность Ω следует из непрерывной зависимости решения уравнения (5) от управления.

Выбрав произвольное управление u ∈ G ¯ u , 0≤t≤t₁ по уравнениям Лагранжа второго рода (5) можно вычислить значения обобщенных координат ( q , q ˙ ) ∈ Ω , а по ним и величину функции Ф ( q , q ˙ , u , λ ) , наибольшее значение которой при фиксированном λ существует в силу ограниченности множества Ω × G ¯ u

Пусть фазовая траектория ( q , q ˙ ) и соответствующее ему управление u ( q , q ˙ ) при заданном λ доставляют максимум функции Ф ( q , q ˙ , u , λ ) на области Ω × G ¯ u , тогда справедлива запись

Теорема [2, 3, 4]. Если управление u ~ ( t ) доставляет минимум функционалу (6) при условиях (2), (3), (4), (7), то существует такой постоянный множитель Лагранжа λ, что при любом t∈[0, t₁] функция Ф переменных ( q , q ˙ , u ) ∈ Ω × G ¯ u достигает в точке ( u ~ ( t ) , q ~ ( t ) , q ~ ˙ ( t ) ) максимума

Построение корректирующей петли авторегулирования ФАПЧ на основе объединенного принципа максимума (ОПМ). В [1] представлена структурная схема простейшей системы ФАПЧ, включающая фазовый дискриминатор, петлевой фильтр, подстраиваемый генератор, крутизна характеристики которого определяет полосу удержания Ω_y.

Выбирая в качестве петлевого фильтра однозвенный RC-фильтр, получим нелинейное дифференциальное уравнение, описывающее систему ФАПЧ [1, с.21]

Здесь φ(t)=φ_c(t)-φ₀(t) - разница фаз сигнала и подстраиваемого генератора; F(φ) - выход фазового дискриминатора, ω н = ϕ ˙ c ( t 0 ) − ϕ ˙ 0 ( t 0 ) - разность угловых частот сигнала и подстраиваемого генератора в начальный момент времени t₀, начальные условия ( ϕ ( t 0 ) , ϕ ˙ ( t 0 ) ) . Данное уравнение допускает представление в форме уравнения Лагранжа второго рода. Следовательно, может быть поставлена задача определения оптимального управления системой ФАПЧ на основе метода ОПМ.

Рассмотрим задачу поиска U ( ϕ , ϕ ˙ ) < | U | , обеспечивающего переход динамической системы

из начальной произвольной точки фазового пространства ( ϕ ( t 0 ) , ϕ ˙ ( t 0 ) ) в конечную (0, 0), такую что

Это математическая формулировка задачи синхронизации.

В соответствии с (9) и полученным на основе объединенного принципа максимума результата (13), анализ условия максимума функции Ф = [ λ U ( ϕ , ϕ ˙ ) + ϕ ] ϕ ˙ с учетом ограничений U ( ϕ , ϕ ˙ ) < | U | позволяет получить по аналогии с [2, 5] следующую структуру петли авторегулирования [7]:

где λ^-1 - неопределенный множитель Лагранжа, L - константа, зависящая от формы линии переключения, ε и D - константы, определяющие соответственно сдвиг линий переключения и диаметр эллипса в фазовом пространстве состояний ФАПЧ. Тогда структура ФАПЧ ОПМ определяется уравнением [7]:

В ходе численного эксперимента получены решения дифференциальных уравнений, описывающих динамику системы ФАПЧ с RC-фильтром (15) и системы ФАПЧ с петлей авторегулирования, полученной на основе метода ОПМ (18). Моделирование проведено для следующих значений параметров: Т=0,014 с; Ω_y=21 рад/с; |U|=5; λ^-1=1; ε=0,001; D=1; L=4. Уравнение фазового дискриминатора имеет вид

F(φ)=sin(φ).

На фиг.3 демонстрируется процесс захвата на временной диаграмме (а) и фазовой плоскости (б).

На фиг.4 представлены зависимости времени захвата t_з для рассматриваемых систем ФАПЧ от начальной расстройки по частоте ϕ ˙ ( t 0 ) для трех значений начальной расстройки по фазе φ(t₀)=0 рад, φ(t₀)=1 рад и φ(t₀)=2 рад.

Приведенные результаты показывают, что время захвата для ФАПЧ с управлением по методу ОПМ примерно в 2-6 раз меньше и практически не зависит от начальных условий. Для данной ФАПЧ в режиме удержания установившееся значение разности фаз φ_y=0, в отличие от ФАПЧ с RC-фильтром, для которой φ_y=arcsin(ω_н/Ω_y)+2πk. Кроме того для ФАПЧ ОПМ наблюдается захват при превышении начальной расстройки по частоте полосы удержания системы ФАПЧ с RC-фильтром, в которой возникают биения (фиг.5).

Таким образом, разработанная система ФАПЧ с корректирующим нелинейным элементом, построенным на основе объединенного принципа максимума, позволяет в несколько раз уменьшить время захвата в сравнении с ФАПЧ с однозвенным RC-фильтром.

Устройство работает следующим образом.

В исходном состоянии эталонный генератор формирует сигнал с фазой φ_ЭГ, который поступает на первый вход первого блока формирования произведения, на второй вход которого поступает сигнал от подстраиваемого генератора с фазой φ_ПГ, на выходе которого формируется спектр сигнала с компонентой sinφ=sin(φ_ЭГ-φ_ПГ) и поступает на первый вход первого блока формирования суммы, на второй вход которого поступает сигнал обратной связи Ω y λ − 1 | U | sin g ( [ D | p ϕ | p ϕ L | ϕ | + ε ] T Ω y + ϕ ) − ω н , на выходе первого блока формирования суммы формируется значение Ω y λ − 1 | U | sin g ( [ D | p ϕ | p ϕ L | ϕ | + ε ] T Ω y + ϕ ) − sin ϕ − ω н , которое поступает на вход RC-фильтра, на первом выходе которого формируется отфильтрованный сигнал и поступает на вход интегрирующего масштабного преобразователя, сигнал с выхода которого поступает на вход ПГ, на первом выходе которого формируется гармонический сигнал и поступает на второй вход первого блока формирования произведения; со второго выхода ПГ, являющегося выходом устройства, снимается выходной сигнал; со второго выхода RC-фильтра сигнал поступает на вход форсирующего звена, на выходе которого формируется сигнал, пропорциональный sinφ, и поступает на вход блока формирования arcsin, на выходе которого формируется сигнал, пропорциональный φ, и с первого выхода полученный сигнал поступает на вход блока формирования производной, на выходе которого формируется сигнал, пропорциональный ϕ ˙ , и с первого выхода полученное значение поступает на вход блока формирования модуля, на выходе которого формируется сигнал, пропорциональный | ϕ ˙ | , и поступает на первый вход второго блока формирования произведения; со второго выхода блока формирования производной полученное значение ϕ ˙ поступает на второй вход второго блока формирования произведения, на выходе которого формируется сигнал, пропорциональный ϕ ˙ | ϕ ˙ | , и поступает на вход четвертого блока формирования произведения, на выходе которого формируется сигнал, пропорциональный D ϕ ˙ | ϕ ˙ | , и поступает на второй вход пятого блока формирования произведения; со второго выхода блока формирования arcsin полученное значение сигнала, пропорционального φ, поступает на вход третьего блока формирования произведения, на выходе которого формируется значение сигнала, пропорционального (L|φ|+ε)^-1, и поступает на первый вход пятого блока формирования произведения, на выходе которого формируется значение сигнала пропорционального ϕ ˙ | ϕ ˙ | L | ϕ | + ε и поступает на вход шестого блока формирования произведения, на выходе которого формируется значение сигнала, пропорционального [ D | ϕ ˙ | ϕ ˙ L | ϕ | + ε ] T Ω y , и поступает на второй вход второго блока формирования суммы; с третьего выхода блока формирования arcsin полученное значение сигнала, пропорционального φ, поступает на первый вход второго блока формирования суммы, на выходе которого формируется значение сигнала, пропорционального [ D | ϕ ˙ | ϕ ˙ L | ϕ | + ε + ϕ ] T Ω y , и поступает на вход блока формирования sign, на выходе которого формируется значение сигнала, пропорционального s i g n [ D | ϕ ˙ | ϕ ˙ L | ϕ | + ε + ϕ ] T Ω y , и поступает на вход седьмого блока формирования произведения, на выходе которого формируется значение сигнала, пропорционального Ω y λ − 1 | U | s i g n [ D | ϕ ˙ | ϕ ˙ L | ϕ | + ε + ϕ ] T Ω y , и поступает на второй вход первого блока формирования суммы.

На входе устройства действует сигнал ЭГ, а с выхода устройства снимается сигнал подстраиваемого генератора, при этом работа устройства продолжается до момента сведения к нулю значения φ.

Источники информации

1. Шахгильдян В.В., Ляховский А.А. Системы фазовой автоподстройки частоты. М.: Связь. 1972. 447 с.

2. Костоглотов А.А., Костоглотов А.И., Лазаренко С.В. Объединенный принцип максимума в информационных технологиях анализа и синтеза: Монография. Ростов-на-Дону: РАС ЮРГУЭС. 2010. 165 с.

3. Андрашитов Д.С., Костоглотов А.А., Лазаренко С.В., Дерябкин И.В. Вариационный метод многопараметрической идентификации динамических систем на основе итерационной регуляризации // Успехи современной радиоэлектроники. 2012. №6. С.67-72.

4. Андрашитов Д.С., Костоглотов А.А., Костоглотов А.И., Лазаренко С.В. Методы многопараметрической идентификации динамических систем на основе объединенного принципа максимума: Монография. Ростов-на-Дону, ЮРГУЭС, 2011 г., 105 с.

5. Костоглотов А.А., Костоглотов А.И., Лазаренко С.В., Кузнецов А.А. Синтез оптимального регулятора на основе использования физических принципов // Нелинейный мир. 2012. №11. С.819-824.

6. Лурье А.И. Аналитическая механика. М.: Гос. изд. физ. - мат. лит., 1961, с.642-648.

7. Костоглотов А.А., Малый В.А., Понкратов А.И., Приймаков С.Н., Чеботарев А.В. Система фазовой автоподстройки частоты в режиме захвата с корректирующей петлей авторегулирования // Успехи современной радиоэлектроники. 2013. №8. С.32-36.

Устройство контура фазовой автоподстройки частоты с обратной связью на основе объединенного принципа максимума, содержащее блок эталонного генератора, блок подстраиваемого генератора, первый блок формирования произведения, RC-фильтр, интегрирующий масштабный преобразователь, отличающееся тем, что в устройство введены блок формирования arcsin, блок формирования sign, блок формирования модуля, блок формирования производной, второй, третий, четвертый, пятый, шестой, седьмой блоки формирования произведения, первый и второй блоки формирования суммы, форсирующее звено, при этом выход первого блока формирования произведения соединен с первым входом первого блока формирования суммы, выход которого соединен с входом RC-фильтра, первый выход которого соединен с входом интегрирующего масштабного преобразователя, выход которого соединен с входом подстраиваемого генератора, первый выход которого соединен со вторым входом первого блока формирования произведения; второй выход подстраиваемого генератора является выходом устройства; второй выход RC-фильтра соединен с входом форсирующего звена, выход которого соединен с входом блока формирования arcsin, первый выход которого соединен с входом блока формирования производной, первый выход которого соединен с входом блока формирования модуля, выход которого соединен с первым входом второго блока формирования произведения, выход которого соединен с входом четвертого блока формирования произведения, выход которого соединен с входом пятого блока формирования произведения, выход которого соединен с входом шестого блока формирования произведения, выход которого соединен со вторым входом второго блока формирования суммы, выход которого соединен с входом блока формирования sign сигнала, выход которого соединен с входом седьмого блока формирования произведения, выход которого соединен со вторым входом первого блока формирования суммы; второй выход блока формирования arcsin сигнала соединен с входом третьего блока формирования произведения, выход которого соединен с первым входом пятого блока формирования произведения; третий выход блока формирования arcsin сигнала соединен с первым входом второго блока формирования суммы.