Способ формирования функциональных-интегральных-дифференцированных квадратурных опорных сигналов

Способ формирования функциональных-интегральных-дифференцированных квадратурных опорных сигналов

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области техники первичного измерительного преобразования физических величин в электрические сигналы и касается способа формирования функционально-интегрированных дифференцированных (далее - ΦИД) квадратурных опорных сигналов (далее - КОС). Предложенное техническое решение (TP) может быть использовано для разработки и изготовления ФИД датчиков КОС. Такие датчики могут найти применение в системах управления, контроля и регистрации вращающихся объектов (ВО), например, одноканальных вращающихся ракет и снарядов, системах стабилизации угловой скорости вращения ВО, следящего регулирования пространственной ориентации ВО и т.д.

Для задания систем отсчета координат ВО и формирования управляющих воздействий в режиме вращения используют так называемые КОС. В математическом представлении опорные сигналы представляют собой первые гармоники совокупности ортонормированных базисных систем функций, например, тригонометрических синусно-косинусных, Лагерра, Эрмита, Радемахера, Адамара, Уолша и т.д. В настоящее время на практике наибольшее распространение получили синусно-косинусные функции, а представляющие эти функции сигналы принято называть КОС.

Первичные измерительные преобразователи, называемые также датчиками, являются важнейшими любой информационной, автоматической и измерительной системы. Выбор способа преобразования физической величины и представления информации о ней в признаках и параметрах сигнала датчика существенно влияет на точность, быстродействие и на уровень сложности процедур ее дальнейшей обработки. В свою очередь это определяет конечный результат функционирования всей системы. Как правило, никакими усложнениями дальнейших алгоритмов обработки информации, помученной с датчиков, нельзя восстановить утраченную первичную информацию, если часть информации утеряна в процессе преобразования физической величин и формировании измерительных сигналов, а быстродействие и точность не соответствуют заложенным требованиям. Особенно это касается управления подвижными и скоростными объектами и быстротекущими процессами, когда необходимо обеспечить работу в режиме реального масштаба времени (РМВ). Опираясь на изложенные соображения, рассмотрим историю вопроса и уровень техники известных способов формирования КОС в известных в настоящее время датчиках.

До бурного развития компьютерной и другой цифровой техники наибольшее распространение в качестве датчиков КОС имели аналоговые синусно-косинусные вращающиеся трансформаторы (CKBT). Способ функционирования которых (см., например, 1, стр. 6-9) состоит в использовании основного закона электромагнитной индукции, сформулированного Фарадеем и уточненного Максвеллом. По закону Фарадея электродвижущая сила индукции пропорциональна скорости изменения магнитного потока во времени, или скорости движения контура относительно магнитного поля, или она может быть обусловлена деформацией поля. Последняя взаимосвязь не отражена в формуле закона Фарадея, но она реально существует и используется при разработке электрических машин. По известному способу ротор с двумя взаимно перпендикулярными синусной и косинусной обмотками соединяют с объектом и вращают вместе с ним относительно статора. А на статоре устанавливают синусную обмотку и обмотку возбуждения, на которую подают переменный ток. При угловом перемещении или вращении ротора относительно статора согласно закону Фарадея на его обмотках формируются синусно-косинусные КОС.

Индукционный способ имеет ряд существенных недостатков. Прежде всего, это недостаточный диапазон допустимых частот вращения, уменьшение точности воспроизведения формы синусно-косинусных зависимостей при повышении частоты вращения. Также это наличие дополнительных погрешностей при изменении нагрузки и условий работы, наличие обратной реакции на объект, неудобства сопряжения с цифровыми системами обработки информации из-за аналоговой формы КОС. К достоинству способа относится то, что на его основе реализуется абсолютных датчик КОС, что имеет преимущество перед датчиками накапливающего типа.

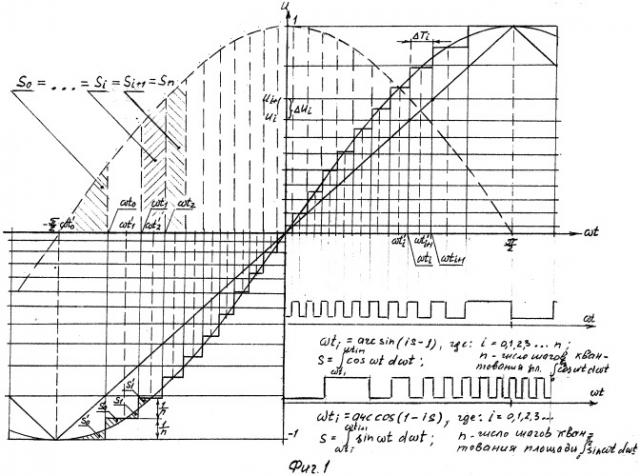
Известен фотоэлектрический способ формирования КОС (2), основанный на преобразовании текущей фазы вращения объекта в совокупность прецизионных цифровых синусно-косинусных сигналов в виде последовательностей счетных импульсов, унитарным число-импульсным кодом, представляющих единичные функции синуса и косинуса, таким образом, что между блоком светоизлучателей и фотоприемников вращают модулирующий диск (растр) с четырьмя модулирующими дорожками, две из которых выполнены в виде сдвинутых между собой на 90° чередующихся прозрачных и непрозрачных 2^m=2n модулирующих площадок, расположенных с переменным по углу шагом и на заданных квантованной решетчатой функцией позициях угла текущей фазы вращения по закону wt_i=arc sin (is-1), где w - угловая скорость вращения объекта, t - время; i - номер площадки от начального отсчета I=0, 1, 2, 3…2n, s = 1 n шаг квантования, а другие две выполнены в виде сдвинутых между собой на 90° прозрачных и непрозрачных полуколец, полученные счетные импульсы считают суммирующим счетом в интервалах, где функции sin wt и cos wt имеют положительное значение, и вычитающим счетом, где они имеют отрицательное значение, а полученные «меандры» sign sin wt и sign cos wt используют для управления алгебраическим счетом импульсов, одновременно полученные цифровые КОС преобразуют в аналоговые. Математическое представление шага s квантования состоит в разбиении на равные по длине отрезки взаимно перпендикулярных единичных радиусов, совпадающих с линиями синуса и косинуса в единичном тригонометрическом круге, в котором вместе с управляемым или контролируемым объектом вращается единичный вектор.

Известный способ имеет высокое быстродействие и точность (задается числом разбиений η), широкий диапазон допустимых частот вращения объекта, а одновременно цифровая и аналоговая форма представления КОС дает удобство сопряжения с любыми системами обработки информации, включая современные цифровые системы на основе ЭВМ. Недостатком является малая информативность, так как КОС представляют только функциональные синусно-косинусные зависимости.

Более информативным и наиболее близким по технической сущности к заявленному TP является предложенный мной способ формирования КОС с представлением их в виде дискретно заданных цифровых интегрированных сигналов (т.е. с воспроизведением первообразных функций) и реализованный в ряде устройств (см. 3, 4, 5, 6). Наиболее близкий известный способ заключается в фотоэлектрическом преобразовании текущей фазы вращения объекта в две последовательности счетных импульсов с переменным периодом следования, представляющие унитарным число-импульсным кодом первообразные функции, а точнее все семейство функционалов ∫ sin wt d wt и ∫ cos wt d wt, расположенных на позициях угла текущей фазы вращения объекта по закону wt_i=arc cos (1-is), где w - угловая скорость вращения объекта, t - время, I=0, 1, 2, 3…n независимая переменная (номер модулирующей площадки), s = 2 n постоянный по площади шаг квантования площадей ∫ 0 π sin wt d wt и ∫ − π 2 π 2 cos wt dwt, произведенного разбиением линиями, параллельными оси ординат на равные между собой по площади площадки ∫ w t i w t i + 1 Sin wt d wt, ∫ w t i w t i + 1 cos wt d wt, и алгебраическом счете по двум каналам полученных счетных импульсов с любыми начальными условиями, которые задаются естественным путем начала и окончания счета, например фронтами полученных «меандров» sign sin wt и sign cos wt.

Наиболее близкий способ обеспечивает высокие точность и быстродействие, высокую информативность за счет формирования интегрированных КОС с удобной для дальнейшей обработки формой представления первообразных функций, которая значительно снижает уровень сложности дальнейшей обработки информации, снижает затраты технических средств и объем вычислительных операций.

Недостатком наиболее близкого известного способа является недостаточная информативность, так как формируются только первообразные функции КОС. Однако в настоящее время в связи с развитием и совершенствованием теории и практики систем автоматического регулирования и управления с целью повышения показателей качества управления (control performance index) в регуляторах применяют пропорционально-интегрально-дифференциальный (ПИД) закон управления (proportional plus integral plus derivative control law; pid-law). При проектировании аналоговых и цифровых ПИД-регуляторов требуется вводить безынерционное пропорциональное, интегрирующее и дифференцирующее звенья. Введение ПИД закона значительно улучшает качественные и количественные характеристики систем автоматического управления (САУ) и производится аппаратными или программными средствами. Но известные алгоритмы цифрового интегрирования и дифференцирования требуют больших объемов вычислительных операций и не всегда физически реализуются. Кроме того, точность известных способов интегрирования и дифференцирования ограничена. Уменьшение шага дискретизации при интегрировании вызывает сначала вычислительные шумы, а затем так называемый «взрыв погрешностей», а при дифференцировании «разбалтывание». Устранить эти недостатки и освободить ЭВМ для решения других задач может помочь совмещение в одном датчике КОС функциональных, первообразных и производных зависимостей.

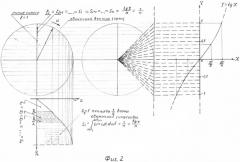
Мной предложен, неоднократно изложен на НТС ЛОМО, одобрен ведущими специалистами КБМ, Коломна, новый способ представления и преобразования информации, на основе которого получены многочисленные авторские свидетельства на изобретения СССР на новые типы датчиков КОС, цифровые способы и устройства управления и контроля параметров вращающихся объектов (СССР, А.с. №№265518, 263567, 265527, 298319 и др. Суть нового способа представления информации состоит в смене ролей физических координат задания сигнала: в качестве независимых координат (аргументов) используются пространственные величины, путь, площадь или объем, а в качестве зависимых координат (функций) время или текущая фаза вращения объекта. Тогда с постоянным шагом квантуется путь или площадь, а шаг квантования сигнала по уровню и времени становится переменным и задается квантованной решетчатой функцией (см. Фиг. 1 и Фиг. 2, где графически и аналитически представлено математическое описание такого представления в виде унитарного число-импульсного кода синусно-косинусных функциональных зависимостей, первообразных и производных функционалов. Причем связь с производными публикуется мной впервые и обладает полной новизной. На Фиг.2 показано, что предложенный способ квантует с постоянным шагом не только площади под полуволнами единичных синусоиды и косинусоиды, но также тангенсы угла наклона касательной, т.е, производные сигналы. Промежуточные математические выкладки вывода позиций wt_i текущей фазы вращения объекта, позиций по уровню сигналов u_i и переменного шага по текущей фазе и по уровню Δu_i не показаны ввиду объемности формул, при желании, экспертизы они могут быть представлены в процессе экспертизы либо останутся моим «ноу-хау».

Указанная цель повышения информативности КОС за счет одновременного формирования функциональных, первообразных и производных сигналов достигается следующим образом. Способ формирования дискретно заданных интегрированных КОС, основанный на вращении между блоком источников света и блоком фотоприемников модулирующего диска с четырьмя дорожками, две из которых состоят и сдвинутых между собой на 90° прозрачных и непрозрачных полуколец, а две другие из сдвитутых между собой на 90° расположенных с переменным шагом прозрачных и непрозрачных модулирующих площадок, формировании двух «меандров» sign sinwt и sign coswt и двух последовательностей счетных импульсов с переменным периодом следования, расположенных на позициях текущей фазы вращения объекта от начального отсчета wt_i=arccos(1-is) и wt_i=arcsin(is-1), где I=0, 1, 2, 3…n=2^m s = ∫ w t i w t i + 1 coswt d wt, алгебраическом счете импульсов по двум каналам, суммирующем счете в интервалах, где «меандры» sign sinwt и sign coswt имеют высокий уровень, и вычитающем счете, где они имеют низкий уровень, и отличается тем, что модулирующие площадки выполняют не одинакового размера как в прототипе, а половинного размера каждого периода их следования, а счет импульсов выполняют одновременно по трем каналам функциональных, первообразных и производных зависимостей, в каждом из которых параллельно ведут алгебраический счет по синусному и косинусному каналу, а управление режимами суммирующего и вычитающего счета производят согласно логике возрастания и убывания функций, а также их первообразных и производных (см. Фиг. 1 и Фиг. 2), которые задают "меандры" sign (sin wt), sign (cos wt) и sign (sin wt) × sign (coswt), а короткие счетные импульсы формируют детектированием фронтов полученных нелинейных последовательностей переменного шага текущей фазы вращения wt. (Конкретный пример организации и схемотехнических решений логики счета с учетом реверса смотреть СССР. А.с. №297567 "Способ формирования прецизионных квадратурных опорных сигналов и устройство для его осуществления").

Таким образом, предложенный способ отличает от известных технических решений аналога (СССР, А.с. №297567) и прототипа (сам способ мной не защищен, но он описан в А.с. СССР. №265518 интегрирующего синусно-косинусного датчика КОС, и технических решениях СССР, А.с. №№263567, 265527, 298319, 265518 и других моих изобретениях) тем, что алгебраический счет нелнейностей текущей фазы вращения управляемого или контролируемого объекта ведут одновременно по шести каналам и используют все отличительные особенности разработанного мной нового метода представления и преобразования информации применительно к синусно-косинусным функциям, которые позволяют закодировать унитарным число-импульсным кодом сами функции, а также их первообразные и производные. Обзор известных разделов высшей математики матанализа, теорий функций и функционалов, тригонометрии, теории и практики цифровой обработки сигналов, известных методов цифрового дифференцирования и интегрирования показал новизну разработанного мной метода представления и преобразования сигналов. Также патентный поиск по основным промышленным странам показал отсутствие близких по технической сущности решений, кроме упомянутых выше А.с. СССР с моим участием. С учетом изложенного заявленное решение удовлетворяет критериям новизны, неочевидности, не вытекает из известного уровня науки и техники и имеет изобретательский уровень.

К основному полезному техническому результату повышения информативности следует добавить и другие полезные эффекты предлагаемого решения. Например, наряду с высокой точность и быстродействием достигается значительное упрощение дальнейших процедур обработки представленных таким образом КОС. Так, не требуется вводить начальные условия интегрирования, как при применении известных алгоритмов, в нашем случае они вводятся без дополнительных затрат аппаратных и программных средств естественно началом и окончанием алгебраического счета импульсов. Если понадобится, это позволит получить все семейство решений функционалов sin wt d wt и Jcos wt d wt (известно, что неопределенный интеграл является простейшим функционалом). Более того, применение такого типа опорного сигнала позволяет реализовать весьма сложную и объемную операцию свертки с сигналом управления вращающегося объекта (заявлено мной отдельно, вх. №003076 от 22.01.2014, регистрационный №2014102071) по довольно простому прямому алгоритму. Полезным достигаемым результатом также является одновременное представление КОС в последовательном унитарном число-импульсном коде, параллельном двоичном и аналоговой форме. Это дает удобство сопряжения с любой системой на основе как цифровых устройств, аналоговых либо их комбинаций.

На Фиг. 1 представлены математическое описание в графической и аналитической форме, демонстрирующее квантование с переменным шагом по уровню и текущей фазе единичного синусного сигнала и первообразной функции косинусного сигнала, выведенное аналитически исходя из квантования по постоянному шагу площадей

s₀=s₁=…=s_i=…s_n= ∫ w t i w t i + 1 sin wt d wt = ∫ w t i w t i + 1 cos wt d wt;

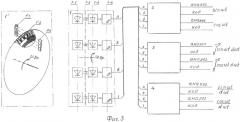
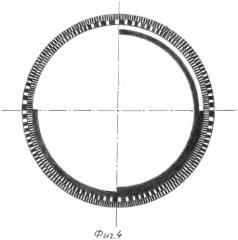
на Фиг. 2 представлено математическое описание в графической и аналитической форме, демонстрирующее применение этого же метода квантования для первообразной и производной функций сигналов, показывающее, что квантование тангенсов угла наклона касательной также происходит с постоянным шагом, то есть и производные функции sin wt/dwt, cos wt/dwt квантуются с постоянным шагом, что позволяет формировать их алгебраическим счетом при условии начала счета импульсов от нулевых значений производных, где tg угла наклона касательной равен нулю; на Фиг. 3 представлены укрупненная функциональная схема примера конкретного устройства для реализации заявленного способа и эскиз механической части датчика; на Фиг. 4 представлен эскиз модулирующего диска датика КОС, на Фиг. 5 представлена структурная схема блока формирования производных (т.е, дифференцированных) сигналов; на Фиг. 6 представлены временные диаграммы работы блока формирования производных.

На Фиг. 1 и Фиг. 2 показан принцип представления КОС в виде последовательных унитарных кодов, собственно нелинейностей текущей фазы вращения, выраженных счетными импульсами в виде двоичного числа, алгебраический счет которых в зависимости от заданных начальных условий счета формирует единичные ортогональные синусно-косинусные зависимости, а также первообразные и производные. При этом точность задается числом шагов квантования и составляет плюс, минус единицу счета, а быстродействие ограничивается только быстродействием применяемых счетчиков импульсов.

Пример реализации датчика 1 на Фиг. 3 содержит блок источников 1-1 света, оптически соединенный через четыре дорожки модулирующего диска 1-2 с блоком фотоприемников 1-3. Модулирующий диск механически соединен с управляемым или контролируемым объектом и вращается вместе с ним с угловой скоростью w вр, при этом на выходе фотоприемников формируются бинарные импульсы двух квадратурных "меандров" и две квадратурные последовательности счетных импульсов. Электрическая схема датчика 1 изображена на функциональной схеме. Модулированные при вращении диска 1-2 сигналы с выходов фотоприемников 1-3 поступают на входы формирователей 1-4, которые выполняют по типовым схема, например, на RS-триггерах, или на триггерах Шмитта для устранения дребезга фронтов и нормировки уровней логического нуля и логической единицы для прменяемого типа микросхем. Нормализованные бинарные сигналы а, б, в, г поступают на входы блока 2 синусно-косинусных КОС, блока 3 первообразных и блока 4 производных КОС.

На Фиг. 4 изображен эскиз одного из варианта выполнения модулирующего диска (растра). Диск содержит 4 модулирующие дорожки, две в виде сдвинутых между собой на 90 прозрачных и непрозрачных полуколец, и две в виде выполненных с переменным шагом 2 прозрачных и непрозрачных модулирующих площадок, расположенных на заданных позициях (см. Фиг. 1 и Фиг. 2).

На Фиг. 5 изображена структурная схема выполнения блоков формирования КОС на примере блока 4 производных, а на Фиг. 6 изображены временные диаграммы работы этого блока. Последовательности а, б поступают сначала на формирователи 1, 2 коротких счетных импульсов и с выходов формирователей на вторые входы блоков 3, 4 управления двоичными реверсивными счетчиками 5, 6 импульсов синусного и косинусного каналов соответственно. На первый вход блока 3 управления счетчиком 5 поступает бинарный сигнал д с выхода перемножителя 7, выполненного на элементе ИСКЛ. ИЛИ. А на первый вход блока 4 управления счетчиком 6 поступает сигнал д1 перемножения с инверсией на элементе 8 НЕ. Блоки 3, 4 в соответствии своей логике управления переключают счетные импульсы на входы +1 суммирующего счета и -1 вычитающего счетчиков 5, 6. Выходы счетчиков 5, 6 соединены с входами 4-квадрантных ЦАП 11, 12, а выходы регистров 13, 14 соединены с информационными входами счетчиков 5, 6. На регистрах (наборные поля) устанавливают в двоичном дополнительном коде начальные нулевые условия счета. Это обусловлено тем, что синусно-косинусные функции имеют 4 квадранта значений, поэтому используются 4-квадрантные ЦАП и двоичный дополнительный код. ЦАП 11, 12 преобразуют двоичный код с выходов счетчиков 5, 6 в двухполярные аналоговые сигналы к, л производных функций от синуса и косинуса. ФНЧ 15, 16 служат для сглаживания ступенек. Режим реверса в данной заявке не рассматривается, так как объем притязаний ограничивается способом формирования КОС, и поэтому в объеме заявки раскрыт только принцип функционирования способа.

Как показано выше, заявленное решение способа обладает новизной и изобретательским уровнем. Реализация способа в реальном устройстве (датчике) не требует новых неизвестных технологий. Модулирующий диск (растр) может быть выполнен методом фотошаблона, схемотехнические решения организации реверсивного счета импульсов известны, одно из них раскрыто в примере реализации способа. Таким образом, заявленное решение соответствует критерию промышленной применимости.

Источники информации

1. Баканов М.В. и др. "Информационные микромашины следящих и счетно-решающих устройств". М., 1977, стр. 6-9, аналог способа.

3. СССР, А.с, №265518, "Фотоэлектрический интегрирующий преобразователь угол - код" (способ-прототип).

4. СССР, А.с. №263567 (способ-прототип).

5. СССР, А.с. №265527 (способ-прототип).

6. СССР, А.с. №298319 (способ-прототип).

7. Ньютон И. "Математические работы", M-Л, ГИТТЛ, 1937.

8. Альберт Д. "Теория сигналов и ее приложения". М., Мир, 1972.

9. Бермант А.Ф. "Курс математического анализа". М., Физматгиз, 1958.

10. Гольденберг Л. "Цифровая обработка сигналов". М., Радио и связь, 1985.

11. Преснухин Л.H. "Фотоэлектрические преобразователи информации". М., Машиностроение, 1974.

Способ формирования квадратурных опорных сигналов, заключающийся в том, что формируют синхронно по частоте и фазе вращения объекта два сдвинутых по фазе на 90° "меандра" sign (sinwt) и sign (coswt), где w - угловая частота вращения объекта, t - время, и две также сдвинутые по фазе на 90° последовательности счетных импульсов с переменным периодом следования путем вращения между оптически связанными между собой блоком из четырех источников света и блоком из четырех фотоприемников модулирующего диска с четырьмя дорожками, две из которых выполняют в виде сдвинутых на 90° полуколец, а две другие - в виде двоичного числа 2^m сдвинутых на 90° и расположенных с переменным шагом прозрачных и непрозрачных модулирующих площадок, суммируют полученные счетные импульсы по двум каналам синуса и косинуса в интервалах высокого уровня "меандров" sign (sinwt) и sign (coswt) и вычитают в интервалах, где эти "меандры" имеют низкий уровень, одновременно преобразуют текущие результаты счета в параллельный двоичный код и в сигналы аналоговой формы, отличающийся тем, что, с целью повышения информативности, прозрачные и непрозрачные модулирующие площадки в каждом шаге квантования выполняют равными, счетные импульсы формируют детектированием фронтов полученных последовательностей "меандров" переменного шага, а алгебраический счет полученных последовательностей коротких счетных импульсов выполняют одновременно по трем каналам формирования синусно-косинусных функциональных, первообразных и производных опорных сигналов в соответствии с логикой возрастания и убывания от нулевых значений синусно-косинусных функций, их первообразных и производных, задаваемых верхним и нижним уровнем "меандров" sign (sinwt), sign (coswt) и sign (sinwt)×sign (coswt).