Измерение параметров, связанных с прохождением текучих сред в пористом материале

Измерение параметров, связанных с прохождением текучих сред в пористом материале

Иллюстрации

Показать все

Реферат

Изобретение относится к измерению физических свойств, связанных с прохождением текучей фазы в пористом материале.

В частности, изобретение находит свое применение для материалов с очень малыми диаметрами проходных каналов в масштабе поры, то есть для материалов с очень большим сопротивлением прохождению текучей среды (в отличие от собственной проницаемости). В качестве неограничивающих примеров этих материалов можно указать сверхплотные породы газоносных пласт-коллекторов (″tight gas reservoirs″), покрывающие породы в потенциальных местах хранения, материалы, используемые в уплотнительных устройствах, композиционные материалы и т.д.

На уровне характерного блока материала прохождение текучей среды через пористое вещество зависит от трех собственных физических характеристик вещества, которыми являются:

- его жидкостная или собственная проницаемость k_I, выраженная в м² или, что более распространенно, в Д (дарси: 1 Д ≈ 0,987 × 10^-12 м²);

- его коэффициент Клинкенберга b, выраженный в Па, если речь идет о малопроницаемом веществе и при прохождении газового потока с низким уровнем давления, или его коэффициент Форхаймера β, выраженный в м^-1, называемый также коэффициентом инерционного сопротивления, если речь идет о высоких уровнях напора, приводящих к инерционным эффектам;

- его пористость ϕ, равная отношению объема пустот материала к его общему объему.

Ни один современный метод не позволяет определять эти три параметра одновременно в ходе одного эксперимента. В частности, пористость часто измеряют отдельно от двух других параметров при помощи пикнометрического метода (гелиевая пикнометрия, ртутная пикнометрия,…) или посредством взвешивания.

Для измерения газопроницаемости материала различают методы в стационарном режиме и методы в нестационарном режиме. См., например, J.A. Rushing et al., Klinkenberg-corrected permeability measurements in tight gas sands: Steady-state versus unsteady-state techniques, SPE 89867 1-11, 2004.

Недостатком способа в стационарном режиме является то, что он требует довольно длительного времени для установления стационарного режима потока, чтобы получить точку измерения. Время достижения этого стационарного режима меняется обратно пропорционально значению k_I и прямо пропорционально квадрату толщины образца. Оно может легко дойти до нескольких часов при очень низкой проницаемости. Раздельное определение собственной проницаемости k_I и коэффициента Клинкенберга b требует нескольких точек измерения и, следовательно, получения такого же числа стационарных состояний. Это может занять много времени, поэтому данный метод не годится для измерения в диапазоне низких значений проницаемости. Кроме того, эта технология требует измерения расхода текучей среды, которое может создать проблемы при очень низкой проницаемости.

Для устранения этих недостатков предпочтительно производить измерение в переходных условиях. Обычно эксперимент при нестационарном состоянии состоит в регистрации изменения дифференциального давления ΔP(t) между концами образца. Каждый конец образца соединяют с соответствующей емкостью и на один из них воздействуют импульсом давления. Этот метод называют ″Pulse decay″. Вариант, в котором выходной резервуар представляет собой бесконечный объем (атмосфера), называется ″Draw down″.

Анализ ΔP(t) дает возможность идентифицировать проницаемость вещества. Часто эта технология не учитывает эффекты Клинкенберга.

В патенте US №2 867 116 был предложен приближенный метод экспериментального определения пористости, эффективной проницаемости (то есть включая эффекты Клинкенберга) и собственной проницаемости. В этих работах значения k_I, b и ϕ определяют приближенно, повторяя эксперимент три раза при постоянном соотношении между значением первоначального импульса давления и первоначальным давлением образца. Первый эксперимент проводят, замеряя время уменьшения импульса давления до заданной доли (например, 55%) от его первоначального значения. Второй эксперимент является идентичным первому, но его осуществляют, просто меняя уровень давления импульса и первоначальное давление образца таким образом, чтобы разность между ними была такой же, что и в первом эксперименте. При этом опять замеряют время, чтобы импульс давления уменьшился до такой же доли (55%) от первоначального значения. Третий эксперимент является идентичным двум первым, но с изменением объема камеры, используемой для создания импульса давления. Определение k_I, b и ϕ на основании этих трех экспериментов осуществляют приближенно, применяя график и используя эмпирическое линейное поведение. На самом деле в общем случае трудно рассчитать реальное влияние этих приближений. Кроме того, следует отметить сложность эксперимента, связанную с устройством и с временем выполнения, необходимым для доведения образца до кондиции при разных давлениях.

В публикации ″A method for the simultaneous determination of permeability and porosity in a low permeability cores″, SPE 15379, 1-11, 1988, S.E. Haskett et al. был предложен способ определения проницаемости k_I, причем без учета эффектов Клинкенберга, и пористости ϕ. Способ требует проведения эксперимента до установления конечного равновесия давления во входном и выходном резервуарах. Он основан на измерении в течение времени разности давления между входным и выходным резервуарами. Эта конфигурация не отличается точностью и не является оптимальной для определения параметров.

В публикации ″A detailed analysis of permeability and Klinkenberg coefficient estimation from unsteady-state pulse decay or draw-down experiments″, Symp. Soc. Core Analysts, Calgary, 10-13 September, 5CA2007-08, 2007, Y. Jannot et al. было предложено пересмотреть метод ″Pulse decay″ без выдвижения каких-либо особых упрощающих гипотез. Просто было указано, что образец представляет собой твердую матрицу, не деформирующуюся под действием потока измерительного газа, и что поток газа является слабосжимаемым, изотермическим и ползучим. В этом контексте физическую задачу, описывающую опыт ″Pulse decay″ в общем случае, можно выразить следующим образом:

∂ ∂ x [ ( P + b ) ∂ P ∂ x ] = φ μ k I ∂ P ∂ t   п р и   0 < x < e   и   t > 0             ( 1 )

при начальных условиях:

P ( 0.0 ) = P 0 i             ( 2 )

P ( x ,0 ) = P 1 i   п р и   x > 0             ( 3 )

и при граничных условиях:

k I S μ V 0 [ P ( 0, t ) + b ] ∂ P ∂ x ( 0, t ) = ∂ P ∂ t ( 0, t )             ( 4 )

k I S μ V 1 [ P ( e , t ) + b ] ∂ P ∂ x ( e , t ) = − ∂ P ∂ t ( e , t )             ( 5 )

где: Р является давлением в момент t и в положении x вдоль образца, при этом x = 0 соответствует входной стороне образца, x = е соответствует его выходной стороне, причем импульс давления прикладывают в t = 0;

S является площадью сечения образца;

е является длиной образца;

V₀ и V₁ соответственно являются объемами входного резервуара (высокое давление) и выходного резервуара (низкое давление), сообщающихся с образцом, в которых первоначально (в t = 0) присутствует давление с соответствующими значениями Р_0i и Р_1i;

µ является динамической вязкостью газа, предположительно постоянной.

В конфигурации ″Draw down″ второе граничное условие заменено классическим условием Дирихле: P(e,t) = P₁ = Р_1i. В данном случае предполагают, что первоначально образец находится под действием атмосферного давления, с которым он в нормальных условиях находится в состоянии равновесия.

На входе образца обязательно присутствует мертвый объем, то есть между вентилем, который изолирует образец от входного резервуара, и входной стороной образца. Желательно, чтобы объем V₀ был очень малым (в идеале порядка объема поры в образце), чтобы повысить чувствительность измерений к пористости ϕ, но в этом случае ее точное определение с целью учета в условии (4) становится очень деликатным, так как предполагает точное знание мертвого объема. Таким образом, существование этого мертвого объема оказывает большое влияние на оценочные значения k_I и b. Кроме того, открывание вентиля в момент начала эксперимента ″Pulse decay″ приводит к расширению текучей среды в мертвом объеме, что влечет за собой термические и гидродинамические помехи, которые, хотя и являются наблюдаемыми, очень трудно учитывать точно при моделировании. Вышеуказанные уравнения (1)-(5) не учитывают эти термические и гидродинамические эффекты.

Ошибка в определении пористости ϕ существенно влияет на оценочные значения проницаемости k_I и коэффициента Клинкенберга b. Качественная оценка этих двух параметров требует таким образом точного знания ϕ, если эту величину используют в качестве входного параметра. Применяемые для этого пикнометрические методы занимают много времени и приводят к оценке собственной пористости, а не пористости под напряжением (коэффициент загрузки), обычно применяемой для анализа реального материала.

Существует потребность в экспериментальном методе, позволяющем улучшить оценку проницаемости k_I и коэффициента Клинкенберга b (для значений низкой проницаемости, вместо которого определяют коэффициент Форхаймера для значений высокой проницаемости). Кроме того, желательно одновременно производить оценку пористости ϕ в ходе одного эксперимента.

В связи с этим изобретением предложен способ оценки физических параметров материала, содержащий следующие этапы:

- образец материала помещают в герметичную камеру таким образом, чтобы входная сторона образца сообщалась с первым объемом и чтобы выходная сторона образца сообщалась со вторым объемом;

- в первом объеме осуществляют модуляцию давления;

- в течение времени измеряют изменения соответствующих давлений в первом объеме и во втором объеме; и

- при помощи дифференциального уравнения, параметрами которого являются собственная проницаемость материала, пористость материала и, по меньшей мере, один другой коэффициент, характерный для материала, и граничным условием которого является изменение измеряемого давления в первом объеме, производят цифровой анализ изменения измеряемого давления во втором объеме для оценки, по меньшей мере, собственной проницаемости и указанного другого коэффициента.

Чтобы устранить проблемы, связанные с мертвым объемом на входе образца, в качестве исходной данной уже берут не только исходную данную, которую единственно рассматривают как значение импульса давления P_0i, которое служит для моделирования изменения P(0,t), для осуществления инверсии. Наоборот, предусматривают резервуар конечного объема V₁ с выходной стороны и рассматривают две отдельные данные, причем обе измеряемые: сигнал давления на входе P(0,t) = P₀(t) и сигнал давления на выходе P(1,t) = P₁(t). Сигнал P₀(t) может служить входным сигналом на этапе анализа, который состоит в цифровой инверсии дифференциального уравнения, производимой на выходном сигнале P₁(t). Поскольку P₀(t) получен в результате измерения, а не моделирования, он может содержать погрешности, связанные с термическими явлениями, с наличием мертвого объема и т.д., хотя это и не является причиной искажения по отношению к модели, используемой в процедуре инверсии.

Другим коэффициентом, характерным для материала и получаемым посредством оценки одновременно с его собственной проницаемостью k_I, обычно является коэффициент Клинкенберга b, если известно, что исследуемый материал находится в интервале низких значений проницаемости (примерно менее 10^-16 м²). Если проницаемость находится в более высоком интервале, другим коэффициентом может быть коэффициент Форхаймера β. Может существовать диапазон проницаемости, для которого в модели можно учитывать одновременно коэффициент Клинкенберга b и коэффициент Форхаймера β.

В случае, когда вместе с собственной проницаемостью k_I определяют коэффициент Клинкенберга b, на этапе анализа производят цифровую инверсию (1) на выходном сигнале P₁(t). Граничное условие (4) заменяют условием Дирихле по давлению P(0,t) = P₀(t), где P₀(t) измеряют при помощи манометра в первом объеме V₀. Физическая задача больше не зависит ни от V₀, ни от мертвого объема, который таким образом можно игнорировать.

Модуляцию давления в первом объеме применяют не просто моментально, а в шкале времени, большей, чем шкала времени импульса давления. Обычно ее производят в шкале времени, зависящей от диапазона проницаемости материала, но, как правило, в течение более одной минуты. Эту модуляцию давления в первом объеме можно, в частности, осуществлять при помощи последовательности импульсов давления.

В варианте выполнения цифровой анализ изменений измеряемых давлений содержит мониторинг изменения во времени пониженной чувствительности давления P₁(t), измеряемого во втором объеме, к собственной проницаемости и изменения во времени пониженной чувствительности P₁(t) к коэффициенту Клинкенберга или Форхаймера. Это позволяет убедиться, что модуляция давления была применена в первом объеме таким образом, чтобы избежать стабилизации соотношения между этими двумя чувствительностями, что не позволило бы правильно оценить проницаемость и соответствующий коэффициент.

В предпочтительном варианте выполнения цифровой анализ изменений измеряемых давлений P₀(t), P₁(t) осуществляют таким образом, чтобы оценить пористость ϕ материала в дополнение к оценке его собственной проницаемости k_I и его коэффициента Клинкенберга b (или Форхаймера β).

В классическом эксперименте типа ″Pulse decay″ чувствительность P₁(t) быстро становится постоянной, причем по истечении достаточно короткого времени, чтобы этот параметр можно было оценить правильно. Чтобы повысить эту чувствительность, следует увеличить число краткосрочных эффектов, чтобы накапливание текучей среды в порах материала происходило многократно в течение эксперимента. Поскольку способ содержит измерение P₀(t), которое становится данной для осуществления инверсии на P₁(t), возможно любое задаваемое изменение P₀(t). Таким образом, на входе образца генерируют последовательность импульсов давления, чтобы активировать емкостное поведение системы с целью облегчения оценки пористости.

Цифровой анализ изменений измеряемых давлений может содержать мониторинг изменения во времени пониженной чувствительности измеряемого давления P₁(t) к пористости. Это позволяет убедиться, что модуляция давления была применена в первом объеме таким образом, чтобы избежать стабилизации этой пониженной чувствительности к пористости, что не позволило бы правильно оценить пористость ϕ.

Для облегчения схождения оценки параметров в некоторых случаях можно производить предварительную оценку собственной проницаемости k_I и коэффициента Клинкенберга b при помощи давлений, измеренных в интервалах времени, в которых давление во втором объеме меняется по существу линейно.

В этом случае предпочтительный вариант выполнения содержит исследование изменения во времени давления во втором объеме. Если это исследование показывает, что давление во втором объеме меняется по существу линейно в зависимости от времени, это давление оставляют изменяться по существу линейно, чтобы получить значения для предварительной оценки собственной проницаемости и коэффициента, после чего в первом объеме применяют новый импульс давления.

Другие отличительные признаки и преимущества настоящего изобретения будут более очевидны из нижеследующего описания неограничивающего примера осуществления со ссылками на прилагаемые чертежи, на которых:

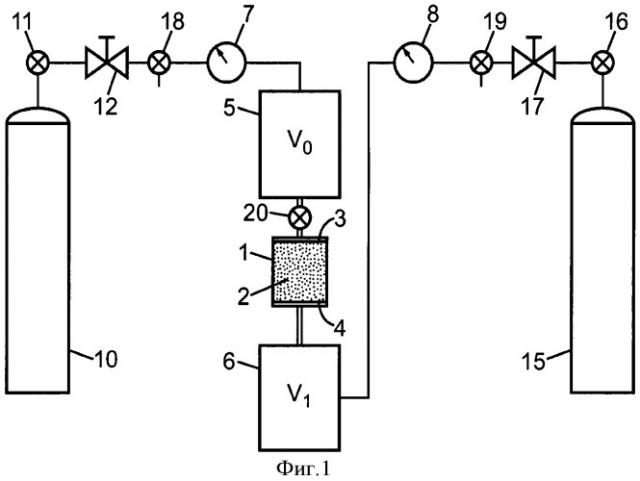
на фиг.1 показана схема установки, используемой для применения заявленного способа оценки физических параметров;

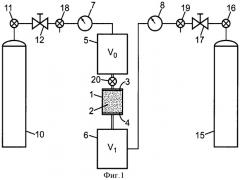
на фиг.2 представлен график, показывающий значения пониженной чувствительности к проницаемости, к коэффициенту Клинкенберга и к пористости в варианте осуществления способа;

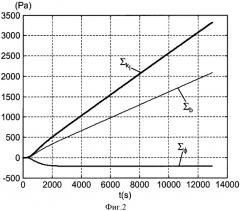
на фиг.3 представлен график, показывающий изменение моделируемого давления на выходе образца в примере применения способа;

на фиг.4 представлен график, показывающий изменение значений пониженной чувствительности к проницаемости, к коэффициенту Клинкенберга и к пористости в примере, представленном на фиг.3;

на фиг.5 представлен график, показывающий изменение соотношения между значениями пониженной чувствительности к проницаемости и к коэффициенту Клинкенберга в примере, представленном на фиг.3;

на фиг.6 представлен график, показывающий изменение соотношения между значениями пониженной чувствительности к проницаемости и к пористости в примере, представленном на фиг.3;

на фиг.7-10 представлены графики, аналогичные графикам, показанным на фиг.3-6, в другом примере применения способа;

на фиг.11-14 представлены графики, аналогичные графикам, показанным на фиг.3-6, в еще одном примере применения способа;

на фиг.15 и 16 представлены графики, показывающие изменение моделируемых давлений на входе и на выходе образца в случае теста, согласно способу;

на фиг.17 и 18 представлены графики, показывающие изменение моделируемых давлений на входе и на выходе образца в испытании на сосновом образце;

на фиг.19 представлен график, показывающий остаточное давление на выходе образца в испытании, изображенном на фиг.17 и 18, при этом остаток представляет собой разность между давлением, вычисленным при помощи модели, описывающей физику испытания, и давлением, измеренным во время испытания;

на фиг.20-22 представлены графики, аналогичные графикам, показанным на фиг.17-19, во время первого испытания на образце породы;

на фиг.23-25 представлены графики, аналогичные графикам, показанным на фиг.17-19, во время второго испытания на этом же образце породы;

на фиг.26-28 представлены графики, аналогичные графикам, показанным на фиг.17-19, во время третьего испытания на этом же образце породы.

Установка, показанная на фиг.1, содержит камеру Хасслера, в которую помещают образец 2 материала, для которого необходимо определить физические параметры в присутствии потока текучей среды. В качестве неограничивающего примера текучей среды можно указать газ, такой как азот или гелий.

Как известно, камера Хасслера представляет собой полый цилиндр, в котором образец 2 цилиндрической формы и с сечением S закрывают с уплотнением, чтобы заставить газ проходить через пористую структуру материала. Образец 2 имеет входную сторону 3 и выходную сторону 4, которые сообщаются с двумя резервуарами 5, 6, объемы которых обозначены соответственно V₀ и V₁.

Манометры 7, 8 позволяют измерять давления в резервуарах 5, 6. Газ, который пропускают через образец, поступает из баллона 10, соединенного с входным объемом V₀ через вентиль 11 и редуктор 12. Со стороны выхода объем V₁ соединен с баллоном-коллектором 15 через вентиль 16 и редуктор 17. Между редуктором 12 и входным объемом V₀ и между редуктором 17 и выходным объемом V₁ установлены другие вентили 18, 19, чтобы выборочно устанавливать сообщение между редукторами и резервуарами 5, 6.

Другой вентиль 20 установлен между входным резервуаром 5 и камерой Хасслера 1 для создания импульсов давления на уровне входной стороны 3 образца. Для приложения первого импульса давления к образцу 2 вентиль 19 позиционируют таким образом, чтобы установить выходной резервуар 6 на исходное давление Р_1i (например, атмосферное давление), тогда как вентиль 20 закрыт. После достижения равновесия давления вентиль 19 закрывают. Открывают вентили 11, 18 и регулируют редуктор 12 по значению давления, необходимому для импульса. Таким образом, газ заполняет входной объем V₀ при необходимом давлении. После этого закрывают вентиль 18 и открывают вентиль 20 для приложения импульса давления к образцу 2. При помощи манометров 7 и 8 отслеживают снижение давления во входном объеме V₀ и повышение давления в выходном объеме V₁. Изменение измеряемых давлений P₀(t) и P₁(t) записывают для последующего цифрового анализа. Чтобы в дальнейшем приложить еще один импульс давления к образцу 2, редуктор 12 регулируют по новому необходимому значению давления, открывают вентиль 18 для заполнения объема Vo при необходимом давлении, затем его закрывают.

Перед приложением первого импульса давления вентиль 20 закрыт, образец 2 находится в состоянии равновесия с выходным объемом V₁ и можно применить первоначальное условие (3). В случае когда эффектами Форхаймера можно пренебречь, физической задачей, решаемой в цифровом виде для оценки параметров, является следующая задача (1)-(3)-(4′)-(5):

∂ ∂ x [ ( P + b ) ∂ P ∂ x ] = φ μ k I ∂ P ∂ t   п р и   0 < x < e   и   t > 0             ( 1 )

при первоначальном условии:

P ( x ,0 ) = P 1 i   п р и   x > 0             ( 3 )

и при граничных условиях:

P ( 0, t ) = P 0 ( t )   п р и   t ≥ 0             ( 4 ' )

k I S μ V 1 [ P ( e , t ) + b ] ∂ P ∂ x ( e , t ) = − ∂ P ∂ t ( e , t )             ( 5 )

В выражении этой задачи давление P₀(t) на входе образца 2 является данной. Физическими параметрами материала образца 2, участвующими в системе, являются его пористость ϕ, его собственная проницаемость k_I и его коэффициент Клинкенберга b.

Возможность оценки параметров на основании сигнала f(t) можно определить посредством исследования чувствительности. В нашем случае можно, например, рассмотреть сигнал f(t) - P₁(t). Чувствительность f(t) к параметру ψ, который необходимо оценить, определяется отношением ∂ ∫ ( t ) ∂ ψ . Из практических соображений чаще всего применяют Σ ψ = ψ ∂ ∫ ( t ) ∂ ψ , что позволяет получить эти величины в единицах давления. Анализ изменения этих величин в зависимости от времени позволяет спрогнозировать возможность оценки параметра ψ на основании сигнала f(t). Эта оценка оказывается возможной, если:

- изменения Σ ψ = ψ ∂ ∫ ( t ) ∂ ψ являются значительными в достаточно большом интервале времени перед шагом временной дискретизации сигнала. Понятие «значительные» означает, что Σψ превышает точность измерительного инструмента (датчики давления 7, 8), используемого для измерения f(t);

- если искомыми являются несколько параметров (например, k_I, b и даже ϕ), значения пониженной чувствительности ко всем этим параметрам необходимо вывести из взаимосвязи, то есть они не должны быть пропорциональны между собой. В противном случае это значит, что изменения, наблюдаемые на f(t), нельзя по отдельности отнести к тому или иному из параметров, что делает их одновременную оценку невозможной на основании только одного сигнала f(t).

На фиг.2 показано изменение во времени значений пониженной чувствительности к проницаемости k_I, к коэффициенту Клинкенберга b и к пористости ϕ, вычисленных в случае только одного импульса давления (типа ″Pulse decay″) в следующих условиях: k_I = 10^-19 м², b = 13,08 бар, ϕ = 0,02, е = 5 см, диаметр образца d = 5 см, V₀ = 10^-3 м³, V₁ = 2,5.10^-3 м³ при исходном давлении 15 бар во входном объеме V₀ и 1 бар в выходном объеме V₁.

Эти значения чувствительности вычисляют на основании сигналов P₁(t), смоделированных при помощи физической модели (1)-(3)-(4′)-(5). При этом по истечении нескольких десятков минут пониженная чувствительность Σ_ϕ к пористости стабилизируется, поэтому после этого времени измерение давления больше не дает представления о пористости ϕ. Таким образом, измерения, произведенные в условиях, представленных на фиг.2, могут оказаться недостаточными для определения пористости ϕ. Тем не менее, они могут быть использованы для определения проницаемости k_I и коэффициента Клинкенберга b, если значение пористости ϕ известно. Эти оценки k_I и b можно получить, не прибегая к точному определению объема V₀ и соответствующего мертвого объема с входной стороны образца 2 и не обращая внимания на возможные погрешности P₀(t), которые после измерения уже не надо вычислять.

Для повышения чувствительности к пористости ϕ и для обеспечения ее оценки следует увеличить число краткосрочных эффектов, чтобы накапливание газа в порах материала происходило многократно в течение всего времени эксперимента. Это проиллюстрировано ниже при помощи трех примеров.

Пример 1 (фиг.3-6)

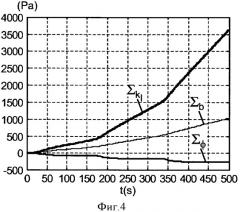
В этом примере анализ чувствительности был произведен посредством моделирования на материале, имеющем собственную проницаемость k_I = 10^-17 м², коэффициент Клинкенберга b = 2,49 бар, пористость ϕ = 0,02 в течение времени эксперимента t_f = 500 с. Были применены три последовательных импульса давления, первый - 5 бар при t = 0, второй - 10 бар при t = t_f/3 и третий - 15 бар при t = 2t_f/3.

Объем входного резервуара 5 был равен V₀ = 10^-3 м³, а объем выходного резервуара 6 был равен V₁ = 2,5.10^-3 м³.

На фиг.3 показано изменение во времени давления P₁(t) на выходе образца. На фиг.4 показано изменение во времени значений пониженной чувствительности Σ_kI, Σ_b и Σϕ давления P₁(t) к собственной проницаемости k_I, к коэффициенту Клинкенберга b и к пористости ϕ. На фиг.5 показано изменение во времени соотношения между значениями пониженной чувствительности Σ_kI, Σ_b к собственной проницаемости k_I и к коэффициенту Клинкенберга b. На фиг.6 показано изменение во времени соотношения между значениями пониженной чувствительности Σ_kI, Σ_ϕ к собственной проницаемости k_I и к пористости ϕ.

Пример 2 (фиг.7-10)

В этом примере анализ чувствительности был произведен в тех же условиях, что и в примере 1, на материале, имеющем собственную проницаемость k_I = 10^-17 м², коэффициент Клинкенберга b = 2,49 бар, пористость ϕ = 0,1 в течение времени эксперимента t_f = 200 с. На фиг.7-10 представлены графики для примера 2, аналогичные графикам на фиг.3-6.

Пример 3 (фиг.11-14)

В этом примере анализ чувствительности был произведен в тех же условиях, что и в примерах 1 и 2, на материале, имеющем собственную проницаемость k_I = 10^-19 м², коэффициент Клинкенберга b = 13,08 бар, пористость ϕ = 0,02 в течение времени эксперимента t_f = 13000 с. На фиг.11-14 представлены графики для примера 3, аналогичные графикам на фиг.3-6.

Все три примера показывают на трех разных материалах, что повышения давления P₁(t) на выходе образца являются измеряемыми величинами, даже если выбрать относительно большой объем V₁ (2,5 литра). Этот объем был специально выбран большим, чтобы подчеркнуть, как можно минимизировать относительную ошибку при измерении. Выбор меньшего объема приводит к более значительным повышениям и можно убедиться, что это не влияет на значения чувствительности. Выбор большого объема для V₁ не мотивирован, как в методе ″Draw down″, получением большого изменения среднего давления в течение времени. Действительно, очень значительное изменение среднего давления в данном случае вызвано последовательными импульсами давления.

Во всех случаях значения чувствительности являются очень значительными и хорошо декоррелированы по парам. Это позволяет произвести одновременную оценку трех параметров k_I, b и ϕ. Если сравнить фиг.4, 8 или 12 с фиг.2, то можно заметить, что модуляция входного давления при помощи нескольких последовательных импульсов существенно улучшает чувствительность к пористости ϕ, что облегчает ее оценку.

Чтобы проиллюстрировать возможность одновременной оценки трех параметров k_I, b и ϕ при помощи заявленного способа, был проведен ряд тестов на основании сигналов, сформированных в цифровом виде при помощи физической модели, при P_0i=1бар. Чтобы лучше представить реальное измерение, на два смоделированных сигнала P₀(t) и P₁(t) был наложен произвольный шум посредством δР₀ = 0,01 × dP × s × Р_0max/3 и δP₁ = 0,01 × dP × s × P_1max/3. Эти шумы таковы, что s является случайным числом со стандартным отклонением от 1, а dP является ошибкой от P₀(t) и P₁(t) (взятые в % от измерений). Коэффициент 3 был взят таким образом, чтобы интервалы P₀(t) ± δР₀ и P₁(t) ± δP₁ включали в себя 99,7% значений, если бы они были действительно измерены. В этих моделях взяли dP = 0,1%, что является типовым значением для датчика давления, исключая случаи 14, 15 и 16, для которых взяли dP = 1%.

Таблица I
Случай №	kI, (м2)	b (бар)	ϕ (%)	V0 (м3)	V1 (м3)	P0i (бар)	dP (%)	N	tf (с)	М
1	10-17	2,49	0,02	10-5	10-2	3	0,1	1000	1000	200
2	10-17	2,49	0,02	10-2	10-2	3	0,1	1000	1000	200
3	10-17	2,49	0,02	10-5	10-2	3	0,1	100	1000	200
4	10-17	2,49	0,02	10-5	10-2	3	0,1	1000	300	200
5	10-17	2,49	0,02	10-5	10-2	3	0,1	1000	1000	50
6	10-17	2,49	0,1	10-5	10-2	3	0,1	1000	1000	200
7	10-17	13,08	0,02	10-5	10-2	3	0,1	1000	100000	200
8	10-17	2,49	0,02	10-2	10-4	3	0,1	1000	1000	200
9	10-17	2,49	0,1	10-2	10-4	3	0,1	1000	1000	200
10	10-17	13,08	0,02	10-2	10-4	3	0,1	1000	10000	200
11	10-17	13,08	0,02	10-2	10-4	5	0,1	1000	10000	200
12	10-17	2,49	0,02	10-2	10-4	3	1	1000	1000	200
13	10-17	2,49	0,1	10-2	10-4	3	1	1000	1000	200
14	10-17	13,08	0,02	10-2	10-4	5	1	1000	10000	200

Параметрами, применяемыми в последовательности тестов, являются параметры, указанные в таблице I, в том числе число N точек измерения давлений P₀(t) и P₁(t), продолжительность tf эксперимента и число М шагов дискретизации в пространстве по толщине е образца, используемых для инверсии задачи (1)-(3)-(4′)-(5). В каждом случае в моменты 0, t_f/3 и 2t_f/3 были применены три импульса давления, доводящие давление во входном резервуаре до P_0i, 2P_0i и 3P_0i. Модуляция давления, примененная в этой последовательности тестов, позволяет в этом случае квалифицировать метод измерения как ″Step Decay″. На фиг.15 и 16 показано изменение давлений P₀(t) и P₁(t) в барах, синтезированных на входе и на выходе образца в случае №1.

Результаты инверсий представлены в таблице II с отклонениями dk_I, db, dϕ в % между исходными значениями k_I, b и ϕ и значениями, полученными посредством инверсионных вычислений.

Таблица II
Случай №	kI (м2)	dkI (%)	b (бар)	db (%)	ϕ (%)	dϕ (%)
1	1,007.10-17	0,10	2,456	0,26	1,96	0,28
2	1,003.10-17	0,11	2,469	0,34	1,97	0,50
3	1,067.10-17	0,61	2,159	1,70	1,60	2,00
4	1.005.10-17	0,09	2,460-	0,31	1,98	0,21
5	1,006.10-17	0,10	2,460	0,26	1,97	0,28
6	1,007.10-17	0,09	2,454	0,28	9,93	0,18
7	1,030.10-1У	0,31	12,55	0,44	1,96	0,25
8	1,004.10-17	0,11	2,460	0,35	1,95	0,53
9	1,002.10-17	0,08	2,472	0,38	9,95	0,38
10	1,027.10-17	0,21	12,58	0,47	1,96	0,30
11	1,007.10-17	0,21	13,08	0,37	2,00	0,30
12	1,001.10-17	1,07	2,49	3,47	2,06	5,11
13	1,003.10-17	0,81	2,42	3,85	9,67	3,81
14	1,088.10-17	1,81	11,24	3,37	1,78	2,99

Эти результаты позволяют сделать следующие выводы:

- точность оценок является высокой (часто лучше чем 1%) для трех оценочных параметров и остается вполне приемлемой с измерительным шумом в 1% от максимального значения давления (случаи №№12-14);

- точность мало зависит от объема Vo. Вполне приемлемым является объем от 0,1 до 10 литров, предпочтительно от 0,1 до 1 литра;