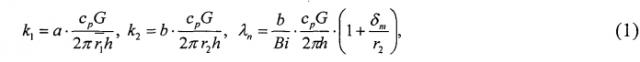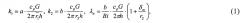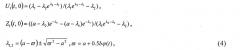Способ определения коэффициентов теплопроводности пород, теплопередачи через насосно-компрессорные трубы и обсадную колонну и длины циркуляционной системы скважины

Способ определения коэффициентов теплопроводности пород, теплопередачи через насосно-компрессорные трубы и обсадную колонну и длины циркуляционной системы скважины

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к нефтегазовой промышленности и касается определения тепловых свойств (тепло - и температуропроводности) пород, слагающих разрез скважины и пласт в целом.

Распространенным методом удаления парафинистых отложений на внутренней поверхности насосно-компрессорных труб (НКТ), уменьшающих живое сечение колонны НКТ и приводящее к снижению ее пропускной способности при добыче высоковязких парафинистых нефтей является тепловой метод депарафинизации скважин с помощью закачки в них теплоносителей, например, горячей нефти.

Для определения тепло- и температуропроводности горных пород разработан метод с применением подвижного сосредоточенного бесконтактного источника тепловой энергии и установка на его основе («Теплофизические свойства горных пород», Бабаев В.В., Будымка В.Ф., Сергеева Т.А. и др. - М.: Недра, 1987, - с.37-38).

Отмеченная установка состоит из подвижной платформы, на которой размещается эталонный образец и исследуемый керн оптического излучателя мощностью 0,5-5,0 Вт, служащего источником тепловой энергии, бесконтактного датчика температуры, представляющего собой низкотемпературный радиометр с чувствительностью 0,10С, самопишущего потенциометра КСП-4 и блока питания.

В эксперименте подвижная платформа с расположенными на ней образцами горных пород перемещается с постоянной скоростью от 0,3 до 1,0 см/с. При этом поверхность образцов нагревается в заданной точке (по линии) лучом лазера и через определенное время температура этой поверхности фиксируется бесконтактным датчиком.

К существенным недостаткам отмеченного метода и установки необходимо отнести отсутствие моделирования термобарических условий залегания горных пород. В частности, как показывает опыт, коэффициенты тепло- и температуропроводности значительно зависят от температуры, что не обеспечивает достоверности измерений при температурах, превышающих комнатную (20°С).

В этой связи представляет интерес метод определения тепловых свойств горных пород в условиях их естественного залегания. В работе (Николаев С.А., Николаева Н.Г., Саламатин А.Н. «Теплофизика горных пород». - Казань: Изд-во КГУ, 1987, с.66-73) представлен скважинный метод определения температуропроводности горных пород пласта, основанный на восстановлении температуры в скважине после ее остановки.

Вокруг действующей скважины естественное температурное поле, как правило, бывает нарушено за счет теплообмена движущегося в ней потока жидкости с окружающей средой. Процесс восстановления температуры, который начинается после остановки последней, зависит от многих факторов, в том числе от предыстории эксплуатации скважины, ее конструкции, тепловых характеристик ее элементов и окружающего горного массива.

Недостатками данной методики являются сложность и длительность проведения эксперимента и отсутствие измерения коэффициента теплопроводности пород.

Кроме отмеченного, оба описанные выше аналога не позволяют определять коэффициенты теплопередачи от теплоносителя в НКТ к потоку в затрубном пространстве в циркуляционной системе скважины.

Наиболее близким к сущности предлагаемого изобретения является модифицированный метод (способы А и В) определения тепло- и температуропроводности горных пород, окружающих скважину, по темпу восстановления температуры бурового раствора после нарушения установившегося теплового поля (Яковлев Б.А. «Прогнозирование нефтегазоносности недр по данным геотермии», М: Недра, 1996, с.47-56).

Способ А учитывает влияние на восстановление нарушенных температур в скважине цементного кольца в затрубном пространстве. При этом рассматривается однородный пласт, вскрытый вертикальной обсаженной скважиной, заполненной жидкостью. Пласт имеет одинаковую температуру t∞, такая же температура и у заполняющей жидкости (длительно простаивающая скважина). После нарушения однородного температурного поля (например, промывкой скважины) оно восстанавливается с темпом, зависящим от интенсивности промывки, конструкции скважины, тепловых свойств затрубного цемента и окружающих пород.

Методика проведения скважинных экспериментов с целью получения исходных данных для определения тепло- и температуропроводности заключается в следующем:

- выбирается длительно простаивающая скважина с достаточно толстыми однородными пластами;

- регистрируется установившаяся естественная температура по стволу скважины (геотермограмма);

- производится промывка скважины (при которой необходимо за 1-2 часа полностью заменить заполняющую ее жидкость и в течение всего этого времени должна регистрироваться температура вытекающей жидкости);

- перед окончанием промывки производится термозамер по стволу скважины в исследуемом интервале глубин;

- последующие термозамеры в этом же интервале производятся через 1, 4, 8, 24 часа простоя скважины после промывки.

Особенностями способа определения тепловых свойств с использованием интегрального преобразования Лапласа являются: учет в математической модели влияния на температурное поле скважины тепловых свойств цементного кольца и возможность применения численных итерационных методов минимизации невязок, реализуемых с помощью ЭВМ.

Способ В (упрощенный статистический метод), реализация которого возможна также с применением ЭВМ, базируется на решении задачи остывания цилиндра бесконечной длины, конечного диаметра в безграничной однородной среде, когда передача тепла в ней от теплоносителя происходит по закону теплопроводности.

В решении задачи допускается, что в пределах изучаемых слоев пород, литологически однородных, изменение теплового поля незначительно; влияние границ раздела (подстилающих и перекрывающих слоев) имеет место только в интервалах, непосредственно прилегающих к этим разделам; влияние конвекции вследствие значительно выраженной вязкости глинистого раствора невелико; диаметр скважины в пределах изучаемого интервала разреза не изменяется.

Недостатком способов А и В является невысокая точность определения средних интегральных значений тепло- и температуропроводности пород по разрезу скважины.

Сопоставление результатов определения теплопроводности λ и температуропроводности а пород по темпу восстановления температуры с данными лабораторных определений, проведенное Б.А. Яковлевым, показывает, что в способах А и В величины тепло- и температуропроводности завышены. При определениях тепловых свойств по статистической методике (способ В) породы по λ, и а слабее дифференцированы (особенно по а).

Принципиальным недостатком прототипа является отсутствие измерения коэффициентов теплопередачи от теплоносителя в НКТ к потоку в затрубном пространстве и длины циркуляционной системы скважины.

Целью изобретения является повышение точности измерения среднеинтегрального значения теплопроводности горных пород по разрезу скважины и определение коэффициентов теплопередачи через НКТ и через обсадную колонну, а также длины циркуляционной системы скважины.

Поставленная цель достигается тем, что в соответствии с известным способом (прототипом) выбирается остановленная скважина, производится ее промывка, регистрируется температура вытекающей промывочной жидкости, при этом в отличие от прототипа закачка горячей жидкости (теплоносителя) производится через затрубное пространство, на входе в него температура этой жидкости меняется по периодическому закону и регистрируется, а коэффициент теплопроводности λ_п и коэффициенты теплопередачи через НКТ k₁ и обсадную колонну k₂, а также длина циркуляционной системы скважины h вычисляются по следующим формулам:

где a, b и Bi находятся из решения системы уравнений:

Условные обозначения:

А_э, ϕ_э - амплитуда и сдвиг фаз, найденные путем обработки замеренной температуры на выходе из циркуляционной системы;

p_э, q_э, - параметры, характеризующие среднюю составляющую температуры на выходе из циркуляционной системы и найденные путем обработки замеренной температуры;

t₁, t_n - безразмерное время начала и конца интервала, в котором ведется обработка замеренной температуры на выходе из циркуляционной системы;

h - длина циркуляционной системы, м;

Т_m - средняя температура на входе в затрубное пространство, °С;

В - температура нейтрального слоя, °С;

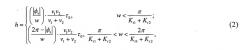
θ_m1(t₁,0), θ_m1(t_n,0) - безразмерные температуры на выходе из НКТ в моменты t₁, t_n, определяемые формулами

где

а функция φ(t) может быть вычислена по формуле

η, ξ, - параметры, определяемые выражениями:

η=Re[ψ₁(iw,0)], ξ=Im[ψ₁(iw,0)],

где i - мнимая единица; Re, Im - действительная и мнимая части функции

K₀(z), K₁(z )- функции Бесселя мнимого аргумента второго рода нулевого и первого порядка, a s=iw;

w=ω·τ₀, ω - частота колебаний температуры, τ₀ - характерное время процесса в часах, указывающее на время, за которое тепловое возмущение распространится вокруг скважины на величину r ¯ 2 ;

v₁, v₂,- скорости потока в НКТ и в затрубном пространстве, м/час;

G=f_1,2 ρv_1,2 - массовый расход, кг/час;

f₁, f₂ - площади поперечных сечений НКТ и затрубного пространства, соответственно, м²;

c_р - теплоемкость кДж/(кг*К);

ρ - плотность, кг/м³;

r₁, r₂ - внутренние радиусы НКТ и обсадной колонны, м;

r ¯ 1 = r 1 − δ p , δ p - толщина слоя парафина на стенке НКТ, м;

k₁, k₂ - коэффициенты теплопередачи от теплоносителя в НКТ к жидкости в затрубном пространстве и от теплоносителя в затрубном пространстве к окружающим скважину породам, соответственно, Вт/(м²*К);

r ¯ 2 = r 2 − δ m , δ m - средняя по длине скважины толщина обсадной колонны, м;

λ_n - коэффициент теплопроводности окружающих скважину пород, Вт/(м²*К);

Bi - безразмерный критерий Био, Bi=k₂ r ¯ 2 /λ_n;

/2„;

K_Г - безразмерный параметр вида K_Г=Гh/(T_m-В).

Предлагаемое изобретение можно описать следующим образом. Перед началом промывки скважину останавливают и выдерживают до тех пор, пока температурное поле в ней не примет вид геотермического распределения. Далее начинается промывка скважины через затрубное пространство. Существенным моментом промывки является то, что температура на входе в него является функцией времени и изменяется по периодическому закону. В этом случае наступает регулярный режим теплообмена, при котором температурное поле в скважине перестает зависеть от начальных данных и определяется периодическими колебаниями температуры на входе. При наступлении такого режима в тепловой обработке скважины температура на выходе из нее содержит много полезной информации о теплообменных процессах в потоке теплоносителя.

Температурное поле в случае регулярного режима теплообмена формируется как суперпозиция двух полей, обусловленного средней температурой на входе в скважину и наведенного периодическими колебаниями температуры. Температура в скважине, обусловленная средней температурой на входе, вычисляется по формулам:

Здесь функции U_1,2, и Z_1,2 определяются следующими выражениями:

U 1 ( t , x ) = ( λ 1 e λ 2 x − λ 2 e λ 2 − λ 1 ( 1 − x ) ) / ( λ 1 e λ 2 − λ 1 − λ 2 ) ,

U 2 ( t , x ) = ( λ 1 e λ 2 − λ 1 ( 1 − x ) − λ 2 e λ 2 x ) / ( λ 1 e λ 2 − λ 1 − λ 2 ) ,

,

,

где λ_1,2, и функция φ(t) могут быть вычислены по формулам (4), (5).

Связь размерных и безразмерных переменных осуществляется следующими выражениями

где τ - время промывки, час;

z - координата сечения скважины, отсчитываемая от устья, м;

T_1,2 - температуры в НКТ и затрубном пространстве соответственно;

Т₀=Гz+В, °С.

Если температура на входе в затрубное пространство скважины изменяется со временем по периодическому закону, то ее всегда можно представить в следующем виде

где A_f - амплитуда, а ω - частота колебаний температуры на входе в циркуляционную систему, или, используя (11), в безразмерной форме

Используя теорию функций комплексного переменного, можно получить формулы, определяющие периодическую составляющую температурного поля в скважине:

где, как и ранее, s=iw, i - мнимая единица; Im - означает мнимую часть соответствующих комплексных функций:

в которых величины ψ₁, ψ₂ вычисляются по формулам:

Величины µ_1,2, ϕ ¯ ( s ) определяются выражениями (6), (7), (8).

Таким образом, при периодическом изменении температуры на входе в затрубное пространство скважины с течением времени наступает регулярный режим теплообмена. При этом температурное поле может быть рассчитано по следующим формулам:

Функции θ_m1(t,x),θ_m2(t,x), θ_p1(t,x), θ_p2(t,x) находятся из выражений (9), (10), (14). Выражения (14)-(16) являются оригинальными и приводятся впервые.

Вычислительные эксперименты, проведенные с использованием формул (16) позволяют сделать следующие выводы:

- амплитуда колебаний температуры на выходе из НКТ существенно отличается от амплитуды колебаний входной температуры. Этот факт объясняется интенсивным теплообменом скважины с окружающим ее массивом горных пород;

- имеется сдвиг по фазе колебаний температуры на входе в затрубное пространство и на выходе из НКТ;

- средняя температура слабо зависит от времени и в достаточно широком диапазоне может быть аппроксимирована линейным законом. В частности, если период колебаний значительно меньше продолжительности промывки скважины, то в интервале времени, имеющем порядок периода колебаний, линейная аппроксимация вполне оправдана.

Первые два факта свидетельствуют о том, что если замерить температуру на выходе и по полученным данным определить амплитуду колебаний выходной температуры и сдвиг фаз, то сравнение этих значений с полученными теоретическими выражениями приводит к двум уравнениям для определения каких-либо параметров, в частности параметров а и b, связанных с коэффициентами теплопередачи. Третий факт говорит о том, что если в процессе закачки на выходе из НКТ скважины произвести замеры температуры и выделить среднюю ее составляющую на текущий момент, то сравнивая ее с θ_m1(t,x) можно получить третье уравнение для вычисления параметра Bi, зависящего от теплопроводности пород.

Обработка экспериментальных данных

Из вышесказанного следует, что для определения тепловых свойств необходимо знать среднюю составляющую температуры, амплитуду колебаний и сдвиг фаз. Вычисление указанных параметров осуществляется по следующему алгоритму. Пусть T_эi, τ_i - замеренные значения температуры и соответствующие моменты времени, 1≤i≤n, где n - число замеров. Ранее было отмечено, что температура на устье скважины (как входная, так и выходная) достаточно хорошо аппроксимируется выражением

где р, q, А, ϕ - параметры, требующие определения из анализа экспериментальных данных.

Для нахождения величин р, q, А, ϕ используется метод наименьших квадратов. Суть его состоит в том, что рассматривается функционал вида

J ( p , q , A , φ ) = ∑ i = 1 n ( p + q ⋅ t i + A sin [ w ⋅ t i + φ ] − θ э i ) 2 .

Здесь t_i, θ_эi - безразмерное время и соответствующее безразмерное значение, замеренной на устье скважины температуры. Значения р, q, А, ϕ находятся из условия минимума рассматриваемого функционала:

Алгоритмы, решающие задачу (18), реализованы в современных компьютерных пакетах. Например, в пакете «Математика» эта задача решается с помощью одного оператора:

FindFit[data, p+q*t+A*Sin[w*t+ϕ], {р,q,A,ϕ},t},

где data - имя массива с экспериментальными данными.

Предложенный алгоритм обработки экспериментальных данных достаточно точно позволяет определить как среднюю составляющую температурного поля, так и периодическую при небольшом количестве замеров. При этом находятся амплитуда колебаний температуры и сдвиг фаз.

Расчетные формулы для определения тепловых свойств.

Оценка тепловых свойств скважины проводится на основе анализа температуры на выходе из НКТ. Учитывая равенства (9), (10), (11), (14), (16), для температуры на выходе из НКТ можно записать:

где i - мнимая единица.

Функция ψ₁(iw,0) является комплексной функцией, то есть

ψ₁(iw,0)=η+iξ, η=Re[ψ₁(iw,0)], ξ=Im[ψ₁(iw,0)].

Следовательно, равенство (19) может быть переписано в виде

где χ=arctg(ξ/η).

Сравнивая выражение (20) с результатами обработки замеров температуры на выходе из НКТ, получаем систему из четырех уравнений:

Индекс «э», как и ранее, указывает на параметры, полученные на основе обработки экспериментальных данных.

Анализ полученной системы показывает, что первые три уравнения могут быть использованы для определения а, b, Bi, а четвертое уравнение дает оценку длины циркуляционной системы. Это связано с тем, что сдвиг фаз практически не зависит от Bi и мало зависит от параметров а, b в широком диапазоне их изменения. Сдвиг фаз определяется частотой колебании температуры и параметром K_1t+K_2t, характеризующим время прохода теплоносителя по всему каналу его движения. Так, при 0<a<1,0<b<4 сдвиг фаз хорошо описывается уравнениями

Из четвертого уравнения вышеуказанной системы находятся формулы для оценки длины циркуляционной системы скважины (2), а первые три уравнения образуют систему (3), определяющую параметры а, b, Bi. Зная величины а, b, Bi и используя формулы (1), можно найти коэффициенты теплопередачи через НКТ и через обсадную колонну скважины k₁, k₂ соответственно, а также коэффициент теплопроводности пород λ_n.

Измеряя температуры на входе в скважину и выходе из НКТ, можно определить их среднюю составляющую, амплитуду колебаний температуры и сдвиг фаз. По экспериментальным данным вычисляются коэффициенты теплопередачи через НКТ и через обсадную колонну, а также коэффициент теплопроводности, окружающих скважину пород, и длину циркуляционной системы скважины.

Полученные результаты, в частности, позволяют более достоверно определять распределение температуры по стволу скважины и вследствие этого повысить эффективность процесса тепловой депарафинизации скважины, что, в конечном счете, увеличит ее текущий дебит.

Таким образом, при осуществлении тепловой обработки скважины в режиме периодического измерения температуры на входе в затрубное пространство с течением времени наступает регулярный режим теплообмена. В этом случае температурное поле не зависит от начальных данных и является суперпозицией средней температуры и периодической составляющей.

Способ определения коэффициентов теплопроводности пород, теплопередачи через насосно-компрессорные трубы и обсадную колонну, а также длины циркуляционной системы скважины, заключающийся в том, что выбирается остановленная скважина, производится ее промывка и при этом регистрируется температура на выходе циркуляционной системы, отличающийся тем, что закачка горячей жидкости (теплоносителя) производится через затрубное пространство, при этом на входе в него температура жидкости меняется по периодическому закону и регистрируется, а коэффициент теплопроводности λ_п и коэффициенты теплопередачи через НКТ k₁ и обсадную колонну k₂ вычисляются по формулам в которых a, b и Bi находятся из решения уравнений системы а длина циркуляционной системы определяется формулами где используются следующие условные обозначения:А_э, ϕ_э - амплитуда и сдвиг фаз, найденные путем обработки замеренной температуры на выходе из циркуляционной системы;p_э, q_э - параметры, характеризующие среднюю составляющую температуры на выходе из циркуляционной системы и найденные путем обработки замеренной температуры;t₁, t_n - безразмерное время начала и конца интервала, в котором ведется обработка замеренной температуры на выходе из циркуляционной системы;h - длина циркуляционной системы, м;T_m - средняя температура на входе в затрубье, °C;B - температура нейтрального слоя, °C;θ_m1(t₁,0), θ_m1(t_n,0) - безразмерные температуры на выходе из НКТ в моменты t₁, t_n, определяемые формулами где , ϖ=a+0.5bφ(t), а функция φ(t) может быть вычислена по формуле η, ξ - параметры, определяемые выражениями:η=Re[ψ₁(iw,0)], ξ=Im[ψ₁(iw,0)],где i - мнимая единица; Re, Im - действительная и мнимая части функции ϕ ¯ ( s ) = 1 s ⋅ s K 1 ( s ) s K 1 ( s ) + B i K 0 ( s ) , K₀(z), K₁(z) - функции Бесселя мнимого аргумента второго рода нулевого и первого порядка, а s=iw;w=ω·τ₀, ω - частота колебаний температуры, τ₀ - характерное время процесса в часах, указывающее на время, за которое тепловое возмущение распространится вокруг скважины на величину r ¯ 2 ;K_t1=τ₁/τ₀, K_t2=τ₂/τ₀, τ₁=h/v₁, τ₂=h/v₂, v₁, v₂ - скорости потока в НКТ и в затрубном пространстве, м/час;G=f_{1, 2}ρv_{1, 2} - массовый расход, кг/час;f₁, f₂ - площади поперечных сечений НКТ и затрубного пространства, соответственно, м²;C_p - теплоемкость кДж/(кг*К);ρ - плотность, кг/м³;r₁, r₂ - внутренние радиусы НКТ и обсадной колонны, м; r ¯ 1 = r 1 − δ p   , δ_p - толщина слоя парафина на стенке НКТ, м;k₁, k₂ - коэффициенты теплопередачи от теплоносителя в НКТ к жидкости в затрубном пространстве и от теплоносителя в затрубном пространстве к окружающим скважину породам, соответственно, Вт/(м²*K); r ¯ 2 = r 2 − δ m , δ_m - средняя по длине скважины толщина обсадной колонны, м;λ_n - коэффициент теплопроводности окружающих скважину пород, Вт/(м²*K);Bi - безразмерный критерий Био, B i = k 2 r ¯ 2 / λ n ;K_Г - безразмерный параметр вида K_Г=Гh/(T_m-B).