Способ определения показателя преломления частиц, образующих многослойную упорядоченную структуру (варианты)

Способ определения показателя преломления частиц, образующих многослойную упорядоченную структуру (варианты)

Иллюстрации

Показать все

Реферат

Изобретение относится к способам определения показателя преломления частиц, образующих трехмерные упорядоченные структуры, такие как фотонные кристаллы или коллоидные кристаллы.

Одной из важнейших характеристик вещества является показатель преломления n, определяющий скорость v распространения в нем электромагнитного излучения (света). Соответственно, важной является задача по его определению.

Существуют различные способы определения показателя преломления вещества.

В частности, известны рефрактометрические способы [1] измерения показателя преломления однородных твердых тел и жидкостей, основанные на законе преломления (законе Снеллиуса) света.

Существуют также интерфенционные способы [1] измерения показателя преломления. Они основаны на явлении интерфенции световых лучей, проходящих через исследуемый (с показателем преломления n₁) и контрольный (с известным показателем преломления n₂) образцы. При этом показатель преломления n₁ исследуемого образца вычисляют исходя из числа наблюдаемых порядков интерференции.

Недостатком указанных способов является то, что они применимы к однородной изотропной среде и не могут быть использованы для определения показателя преломления частиц, образующих упорядоченную дисперсную структуру.

Известен также иммерсионный способ [2] определения показателя преломления, при котором частицы исследуемого вещества помещают в различные жидкости с известными показателями преломления. При совпадении показателей преломления исследуемого вещества с показателем преломления жидкости система становиться прозрачной. Таким образом определяют показатель преломления исследуемого вещества. В отличие от предыдущих данным способом можно определять показатель преломления частиц произвольной формы. Недостатком указанного способа является то, что для определения показателя преломления n_p частиц исследуемого вещества необходимо подбирать жидкости (или их смеси) с известными показателями преломления n_env. При этом если n_p не совпадет ни с одним из n_env, то данным способом показатель преломления исследуемого вещества не будет определен.

Изобретение направлено на решение задачи определения показателя преломления n_p частиц, образующих упорядоченную многослойную (трехмерную) дисперсную структуру, такую как фотонный кристалл или коллоидный кристалл, без ограничения на совпадение показателя преломления частиц с показателем преломления окружающей среды.

Технический результат, который может быть получен при осуществлении заявленного способа, заключается в определении показателя преломления n_p частиц многослойной структуры на длине волны λ_PBG минимума коэффициента когерентного пропускания T_PBG фотонной запрещенной зоны (ФЗЗ) структуры в окружающей среде с известным спектром показателя преломления n_env, при этом для определения n_p на других длинах волн структуру помещают в другие окружающие среды с известными спектрами показателя преломления, в результате чего изменяют λ_PBG, при этом в отличие от известных способов n_env не должны совпадать с n_p.

Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения показателя преломления частиц упорядоченной многослойной структуры, включающем измерение спектра коэффициента когерентного пропускания T_c структуры, помещенной в окружающую среду с известным спектром показателя преломления n_env, нахождение по измеренному спектру T_c длины волны λ_PBG, на которой имеет место минимум пропускания T_PBG фотонной запрещенной зоны, осуществляют путем нахождения такого значения показателя преломления n_p,ret частиц, при котором спектральное положение λ_PBG,ret рассчитанного минимума фотонной запрещенной зоны совпадет с измеренным λ_PBG, либо спектральное положение λ_PBG,ret и значение T_PBG,ret рассчитанного минимума фотонной запрещенной зоны совпадут соответственно с измеренными λ_PBG и T_PBG, при этом для определения показателя преломления на других длинах волн структуру помещают в другие окружающие среды с известными спектрами показателя преломления n_env.

Сущность изобретения поясняется чертежами, где на:

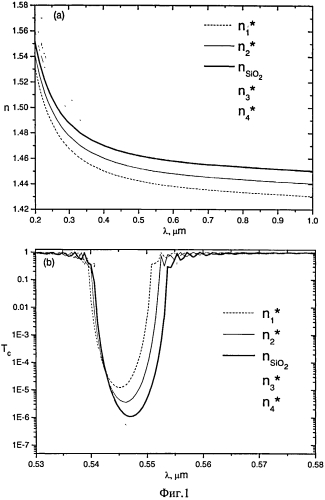
Фиг.1 (a) показаны спектры показателя преломления частиц оксида кремния SiO₂ ( n S i O 2 , жирная линия) и частиц с показателями преломления n 1 * = n S i O 2 − 0 . 0 2 , n 2 * = n S i O 2 − 0 . 0 1 , n 3 * = n S i O 2 + 0 . 0 1 , n 4 * = n S i O 2 + 0 . 0 2 (тонкие линии).

Фиг.1(b) - спектры коэффициента когерентного пропускания T_c мультислоя частиц SiO₂ (жирная линия) и мультислоя частиц с показателем преломления n 1 * = n S i O 2 − 0 . 0 2 , n 2 * = n S i O 2 − 0 . 0 1 , n 3 * = n S i O 2 + 0 . 0 1 , n 4 * = n S i O 2 + 0 . 0 2 (тонкие линии) в метаноле. Диаметр частиц D=0.2 мкм, коэффициент заполнения монослоя (отношение площади проекций всех частиц слоя к площади слоя, на которой они расположены) η=0.5, функция σ(u)=σ₀u, где σ₀=0.01, число монослоев N_mnl=200, расстояние между соседними монослоями (между плоскостями, проходящими через центры частиц в соседних монослоях) h=0.2 мкм.

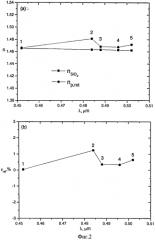
Фиг.2(a) - спектр показателя преломления SiO₂ ( n S i O 2 , по данным [3], квадраты) и определенные (найденные) значения показателя преломления n_p,ret частиц по данным о λ_PBG работы [4]. Расчеты выполнены для многослойной системы, состоящей из монослоев с треугольной решеткой из монодисперсных сферических частиц для значений λ_PBG, обозначенных цифрами 1, 2, …, 5: 1 - система расположена в воздухе, расстояние между соседними монослоями h=0.1715 мкм, число монослоев N_mnl=100; 2 - метаноле, h=0.1719 мкм, N_mnl=200; 3 - этаноле, h=0.1724 мкм, N_mnl=250; 4 - циклогексане, h=0.1715 мкм, N_mnl=500; 5 - толуоле, h=0.169 мкм, N_mnl=400. Диаметр частиц D=0.2 мкм, коэффициент заполнения монослоев η=0.9, функция σ(u)=σ₀u, где σ₀=0.001.

Фиг.2(b) - относительная погрешность восстановления (по данным фиг.2a).

Известно, что спектр коэффициента когерентного пропускания и отражения пространственно упорядоченной многослойной структуры, состоящей из монослоев частиц, имеет диапазон длин волн, в котором частично или полностью подавляется прохождение света через структуру. В этом же диапазоне имеет место резкое возрастание отражения. Этот диапазон длин волн называют фотонной запрещенной зоной (ФЗЗ). Эффект ФЗЗ обусловлен периодичностью структуры в направлении падающей волны.

Известно, что спектральное положение λ_PBG и значение T_PBG минимума ФЗЗ зависят от относительного показателя преломления частиц структуры (см. Фиг.1). Изменяя показатель преломления окружающей структуру среды, можно изменять относительный показатель преломления частиц и, тем самым, λ_PBG и T_PBG минимума ФЗЗ и таким образом находить показатель преломления частиц на разных длинах волн путем сравнения рассчитанных и измеренных значений λ_PBG и T_PBG.

Определение показателя преломления n_p частиц состоит в следующем. Измеряют спектр коэффициента когерентного пропускания упорядоченной - многослойной системы монослоев частиц в окружающей среде с известным спектром показателя преломления n_env и находят спектральное положение (то есть длину волны) λ_PBG минимума ФЗЗ и значение T_PBG на этой длине волны коэффициента когерентного пропускания. После этого рассчитывают ряд значений коэффициента когерентного пропускания T_c на длине волны λ_PBG для диапазона возможных (предполагаемых) n_p и находят такое значение показателя преломления n_p,ret частиц, при котором рассчитанное значение минимума T_c будет наиболее близко к T_PBG. Полученное значение n_p,ret считают определенным (найденным) показателем преломления частиц на длине волны λ_PBG.

Способ позволяет определять показатель преломления частиц n_p и в случае, когда известно только спектральное положение λ_PBG минимума ФЗЗ, например при отсутствии данных о значении T_PBG или невозможности его точного измерения. При этом рассчитывают ряд значений коэффициента когерентного пропускания T_c на длине волны λ_PBG для диапазона возможных (предполагаемых) n_p и находят такое значение показателя преломления n_p,ret частиц, при котором имеет место минимальное значение минимума Т_с. Полученное значение n_p,ret считают определенным (найденным) показателем преломления частиц на длине волны λ_PBG.

Для нахождения именно минимума, а не просто наименьшего значения на спектре T_c системы, рассчитывают значения ее коэффициента когерентного пропускания на двух соседних, достаточно близких к λ_PBG длинах волн: λ_PBG±Δλ, при этом значения T_c на этих длинах волн должны быть больше, чем на длине волны λ_PBG. Также предполагают, что показатель преломления частиц на длинах волн λ_PBG±Δλ совпадает с их показателем преломления на λ_PBG. Для определения показателя преломления частиц на других длинах волн систему помещают в другие окружающие среды, измеряют новые спектры и производят расчеты для новых λ_PBG и T_PBG.

Описанный выше способ определения показателя преломления частиц может быть осуществлен с использованием следующего подхода.

Упорядоченная структура частиц, такая как фотонный кристалл или коллоидный кристалл, может быть представлена в виде набора плоскопараллельных пространственно упорядоченных монослоев частиц.

Существует метод расчета радиальной функции распределения пространственно упорядоченного монослоя частиц, расположенных в узлах неидеальных двумерных периодических решеток (двумерных планарных фотонных кристаллов) [5, 6], позволяющий рассчитывать в квазикристаллическом приближении (ККП) теории многократного рассеяния волн коэффициенты когерентного пропускания и отражения такого монослоя. Суть метода состоит в следующем. Центр любой частицы в монослое выбирается за начало координат. Относительно него рассчитываются радиусы координационных окружностей идеальной решетки (идеального двумерного кристалла) и число центров частиц, лежащих на каждой из них. Радиальная функция распределения частиц такого кристалла представляет собой набор бесконечно узких пиков на расстояниях, равных радиусам координационных окружностей. Реальные кристаллы имеют неидеальную решетку с "размытыми" координационными окружностями. В работах [5, 6] было показано, что выражение для расчета радиальной функции распределения g(u) реального двумерного кристалла (т.е. регулярно упакованного монослоя с неидеальной решеткой) может быть записано в виде:

g ( u ) = ρ 0 − 1 ∑ i N i 2 π   R i 1 2 π σ ( u ) e x p ( − ( u − R i ) 2 2 σ 2 ( u ) ) .   ( 1 )

Здесь σ(u) - функция размытия, характеризующая "размытие" (уширение) координационных окружностей фотонного кристалла в зависимости от расстояния и относительно начала координат. Целесообразно использовать линейную функцию размытия:

σ ( u ) = σ 0 ( a u + b ) .       ( 2 )

В формулах (1) и (2) параметр u=R/D - безразмерное расстояние, выраженное в диаметрах D частиц (u≥1); R - расстояние в плоскости монослоя относительно начала координат, связанного с центром любой частицы; ρ₀ - средняя числовая концентрация частиц в монослое; N_i - число центров частиц, находящихся на координационной окружности с радиусом R_i идеального кристалла; σ₀ - безразмерная начальная дисперсия радиусов координационных окружностей, выраженная в диаметрах частиц; а и b - коэффициенты, зависящие от коэффициента заполнения слоя, типа решетки и σ₀. Изменяя σ₀, можно задавать степень упорядоченности моделируемого кристалла, а изменяя коэффициенты а и b - "дальность" его пространственного порядка.

Используя описанный метод, в ККП рассчитываются амплитудные коэффициенты когерентного пропускания и отражения отдельных монослоев, из которых состоит исследуемая пространственно упорядоченная многослойная система.

Расчет коэффициентов когерентного пропускания и отражения многослойной системы, состоящей из таких монослоев, осуществляется в рамках метода матрицы переноса (ММП) [7] с использованием полученных в ККП амплитудных коэффициентов когерентного пропускания и отражения монослоев.

Таким образом, описанный метод моделирования радиальной функции позволяет в рамках ККП находить характеристики пропускания и отражения отдельных монослоев, на основе которых, используя ММП для многослойной системы, решается задача определения показателя преломления частиц, образующих многослойные (трехмерные) упорядоченные дисперсные структуры.

Как видно из результатов, представленных на Фиг.1, при изменении показателя преломления частиц изменяется как положение, так и глубина ФЗЗ. Эта особенность изменения спектра пропускания многослойной системы лежит в основе заявленного способа.

Заявленный способ был проверен на экспериментальных данных работы [4], в которой приведены результаты измерения спектров многослойной структуры частиц оксида кремния SiO₂ (искусственного опала) в воздухе, метаноле, этаноле, циклогексане и толуоле. На Фиг.2 показаны (a) - значения показателя преломления SiO₂ ( n S i O 2 , по данным работы [3]) и значения показателя преломления частиц n_p,ret, определенные (найденные) описанным выше способом по данным о спектральном положении λ_PBG минимума ФЗЗ работы [4] и (б) - относительная погрешность определения ε_rel показателя преломления, рассчитываемая по формуле

ε r e l = ( n p , r e t − n p ) n p × 1 0 0 % ,       ( 3 )

где n p = n S i O 2 _.

Из приведенных на Фиг.2 результатов видно хорошее совпадение определенных (найденных) значений показателя преломления частиц со значениями показателя преломления оксида кремния (|ε_rel|<1.5%).

Источники информации, принятые во внимание.

1. Физическая Энциклопедия. Статья "Рефрактометр", Москва, "Большая Российская энциклопедия", с.386 (1994).

2. В.Б. Татарский. Кристаллооптика и иммерсионный метод исследования минералов, Москва, "Недра", 1965.

3. E.D. Palik, editor, Handbook of optical constants of solids (Academic, San Diego, 1985).

4. V.N. Bogomolov, S.V. Gaponenko, I.N. Germanenko, A.M. Kapitonov, E.P. Petrov, N.V. Gaponenko, A.V. Prokofiev, A.N. Ponyavina, N.I. Silvanovich, S.M. Samoilovich, "Photonic band gap phenomenon and optical properties of artificial opals", Phys. Rev. E, 55, 7619-7625, (1997).

5. Miskevich A.A., Loiko V.A., "Two-dimensional planar photonic crystals: Calculation of coherent transmittance and reflectance at normal illumination under the quasicrystalline approximation", JQSRT, 112, 1082-1089 (2011).

6. A.A. Мискевич, B.A. Лойко. "Когерентное пропускание и отражение двумерного планарного фотонного кристалла", ЖЭТФ, 140, №1(7), 5-20 (2011).

7. C.C. Katsidis, D.I. Siapkas, "General transfer-matrix method for optical multilayer systems with coherent, partially coherent, and incoherent interference." Appl. Opt. 41, 3978-3987 (2002).

1. Способ определения показателя преломления частиц, образующих упорядоченную многослойную дисперсную структуру, включающий измерение спектра коэффициента когерентного пропускания Т_c(λ) структуры, помещенной в окружающую среду с известным спектром показателя преломления n_enν(λ), где λ - длина волны, нахождение по измеренному спектру Т_c(λ) длины волны λ_PBG, на которой имеет место минимум коэффициента когерентного пропускания фотонной запрещенной зоны, и определение на этой длине волны показателя преломления частиц путем нахождения такого его значения n_p,ret, при котором рассчитанный минимум коэффициента когерентного пропускания имеет наименьшее значение.

2. Способ определения показателя преломления частиц, образующих упорядоченную многослойную дисперсную структуру, включающий измерение спектра коэффициента когерентного пропускания Т_c(λ) структуры, помещенной в окружающую среду с известным спектром показателя преломления n_enν(λ), где λ - длина волны, нахождение по измеренному спектру Т_c(λ) длины волны λ_PBG на которой имеет место минимум коэффициента когерентного пропускания фотонной запрещенной зоны, и значения T_PBG коэффициента когерентного пропускания на этой длине волны и определение на λ_PBG показателя преломления частиц путем нахождения такого его значения n_p,ret, при котором на этой длине волны рассчитанное значение минимума коэффициента когерентного пропускания наиболее близко к измеренному T_PBG.

3. Способ по п.2, отличающийся тем, что структуру помещают в разные окружающие среды, в результате чего изменяют длину волны минимума фотонной запрещенной зоны.