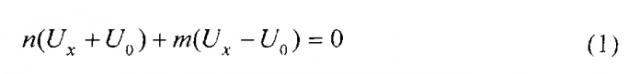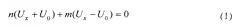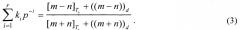Способ интегрирующего аналого-цифрового преобразования напряжения

Способ интегрирующего аналого-цифрового преобразования напряжения

Иллюстрации

Показать все

Реферат

Изобретение относится к электроизмерительной технике.

Цель изобретения - повышение точности.

Известны способы интегрирующего аналого-цифрового преобразования напряжения: патент ФРГ №2214602, кл. G01R, 19/26, 04.09.75; Орнатский П.П. Автоматические измерения и приборы. Киев: Вища школа, 1973, с.435-437. В данных способах имеют место пропуски информации о входном напряжении.

Среди всех известных способов осуществляющих аналого-цифровое преобразование без пропусков информации наиболее высокая точность достигнута в способе, известном в зарубежной литературе как способ сигма-дельта (ΣΔ) аналого-цифрового преобразования [3-5]. Преобразователи, реализующие данный способ, называют ΣΔ-АЦП (в некоторых источниках ΔΣ-АЦП). Ряд иностранных фирм, в том числе Analog Devices, Texas Instruments, Linear Technology и другие, освоили выпуск ΣΔ-АЦП в интегральном исполнении с разрешением до 24 двоичных разрядов.

Данный способ интегрирующего аналого-цифрового преобразования основан на формировании интервала преобразования, состоящего из конечного числа интервалов времени фиксированной длительности, и формировании в течение каждого интервала преобразования непрерывной развертывающей функции путем интегрирования суммы или разности входного и опорного напряжений в течение каждого интервала времени фиксированной длительности, причем изменение полярности опорного напряжения осуществляется в момент времени, соответствующий началу текущего фиксированного интервала времени, если на предыдущем фиксированном интервале времени происходит изменение полярности развертывающей функции, при этом результат преобразования определяют как произведение масштабирующего коэффициента и опорного напряжения, причем масштабирующий коэффициент вычисляют как отношение разности всех интервалов времени фиксированной длительности, соответствующих подключениям положительного и отрицательного опорных напряжений в течение интервала преобразования, к длительности интервала преобразования.

На Фиг.1 приведена структурная схема ΣΔ-АЦП первого порядка (порядок определяется количеством интеграторов). Он состоит из ΣΔ-модулятора первого порядка и цифрового фильтра 8 (ЦФ). Модулятор первого порядка содержит интегратор 2 (И), компаратор 4 (К), триггер 7, одноразрядный ЦАП, работа схемы тактируется генератором тактовых импульсов 6 (ГТИ) частотой f₀, соответствующей интервалам времени фиксированной длительности T₀. Ключ 3 в составе одноразрядного ЦАП осуществляет коммутацию положительного +U₀ и отрицательного -U₀ опорных напряжений, формируемых источником опорных напряжений 5 (ИОН). Таким образом, в течение каждого интервала времени фиксированной длительности T₀ на вход интегратора поступает входное преобразуемое напряжение U_x, сложенное с помощью сумматора 1 с положительным +U₀ или отрицательным +U₀ опорным напряжением.

Работу схемы поясняют временные диаграммы, показанные на Фиг.2. Развертывающая функция R(t) формируется интегратором 1. Момент перехода развертывающей функции через нулевой уровень фиксируется компаратором 4. Результат сравнения развертывающей функции с нулевым уровнем (логический «0» или логическая «1») в момент прихода очередного тактового импульса, соответствующего интервалу времени фиксированной длительности Т₀, с помощью триггера 7 устанавливается на входе одноразрядного ЦАП и сохраняется до начала следующего интервала T₀. Бинарный поток с выхода триггера, имеющий частоту f₀, несет информацию о величине входного напряжения: если входное напряжение растет, стремясь к значению положительного опорного напряжения +U₀, число логических «0» в потоке увеличивается, а число «1» уменьшается, и наоборот, если входное напряжение стремиться к значению отрицательного опорного напряжения -U₀, число логических «0» в потоке снижается, а число «1» увеличивается. Результат преобразования вычисляется ЦФ 8 на каждом интервале преобразования T_П, соответствующем частоте дискретизации f_Д входного сигнала, как произведение масштабирующего коэффициента и опорного напряжения. Масштабирующий коэффициент находится преобразованием выборки бинарных данных с выхода триггера 7, соответствующей текущему интервалу преобразования, как отношение разности количества логических «1» и количества логических «0» в выборке к их сумме (т.е. их общему количеству на интервале преобразования).

В соответствии с описанным способом преобразования в ΣΔ-АЦП происходит непрерывно-дискретное уравновешивание интегрального значения суммы входного и опорного напряжений (U_x+U₀) интегральным значениям их разности (U_x-U₀). Если за время преобразования (T_П) процесс уравновешивания был завершен и при этом количество интервалов дискретизации, в которых интегрировалась сумма напряжений, равно n, а разность - m, можем записать следующее уравнение:

В остальных случаях имеет место методическая погрешность, называемая в известных источниках погрешностью квантования [3, 4]. Введем вместо U_x нормированную переменную k, лежащую на интервале 0≤k<1, т.е. U_x=kU₀ и, рассматривая входной сигнал, как любое действительное число, принимающее N=p^r равноотстоящих значений на этом интервале (где 1/N - разрешающая способность АЦП, r - количество разрядов преобразования, p - основание системы счисления), можем записать следующее выражение:

где k_i - разрядные коэффициенты 0≤k<p. Выражение (2) можно рассматривать как математическую модель ΣΔ-преобразования во временной области.

В существующих ΣΔ-АЦП время преобразования T_П принимает ряд фиксированных значений и, следовательно, сумма (m+n) задается фиксированным значением. Поэтому процесс полного уравновешивания может быть осуществлен только для фиксированного числа точек входного диапазона k, в остальных точках будет иметь место погрешность квантования. Например, для десятичной системы счисления (p=10) и разрешающей способности 10^-6 необходимо иметь 6 разрядов (r=6), при (m+n)=100 имеется 98 фиксированных значений.

Известные направления, связанные с совершенствованием ΣΔ-АЦП, заключаются в следующем:

- повышении порядка модулятора, другими словами в увеличении числа интегрирующих и суммирующих звеньев. Как отмечается в [3, 4], такие системы не могут обеспечить устойчивость при всех входных воздействиях, причем неустойчивость сохраняется даже после того, как вызвавший ее сигнал будет снят;

- применении многокаскадной архитектуры, основывающейся на построении взаимосвязанных каскадов первого порядка. Однако в составе подобных систем используются цифровые дифференциаторы, применение которых существенно повышает требования ко всем высокочастотным шумам в структуре ΣΔ-АЦП;

- уменьшением длительности T₀, т.е. увеличении объема промежуточных бинарных данных на каждом интервале преобразования. Для этого интегратор реализуется по схеме на переключаемых конденсаторах и формируется максимально возможный для данной элементной базы режим быстродействия системы "интеграторы-квантователь-ЦАП". Данное направление ограничено возможностями элементной базы;

- применении многоразрядной структуры. Данные АЦП имеют в своем составе n-разрядный АЦП (в качестве компаратора) и n-разрядный ЦАП. Основным недостатком таких структур является то, что линейность системы зависит от линейности ЦАП и для достижения 16-разрядного разрешения требуется лазерная подгонка [3, 4], поэтому для создания ЦАП с соответствующими характеристиками используют алгоритм скремблирования, который по своим параметрам пропорционален прямому каналу преобразования [3, 4].

Таким образом, именно применение всех указанных выше методов совершенствования характеристик ΣΔ-АЦП позволяет получить высокую точность (24 разряда) данных АЦП. Естественно, такой подход ведет к значительному усложнению структуры преобразователей и в ряде случаев к снижению эксплуатационных характеристик (например, значительное увеличение потребляемой мощности).

Предлагаемый способ интегрирующего аналого-цифрового преобразования призван обеспечить повышение точности АЦП на основе ΣΔ-преобразования без существенного увеличения аппаратных затрат. Задача будет решаться на примере структуры первого порядка, поскольку она является основой для использования всех известных методов совершенствования [3, 4]. Другими словами, указанные методы совершенствования могут также применяться и к предлагаемому способу.

С целью повышения точности в способе интегрирующего аналого-цифрового преобразования, основанном на формировании интервала преобразования, состоящего из конечного числа интервалов времени фиксированной длительности, и формировании в течение каждого интервала преобразования непрерывной развертывающей функции путем интегрирования суммы или разности входного и опорного напряжений в течение каждого интервала времени фиксированной длительности, при этом результат преобразования определяют как произведение масштабирующего коэффициента и опорного напряжения, причем масштабирующий коэффициент вычисляют как отношение разности всех интервалов времени фиксированной длительности, соответствующих подключениям положительного и отрицательного опорных напряжений в течение интервала преобразования, к длительности интервала преобразования, формируют дополнительные интервалы времени фиксированной длительности, причем длительность дополнительных интервалов времени фиксированной длительности задается меньше длительности интервалов времени фиксированной длительности в целое число раз, изменение полярности опорного напряжения осуществляется в момент времени, соответствующий началу текущего фиксированного интервала времени, если на предыдущем фиксированном интервале времени происходит изменение полярности развертывающей функции, причем все нечетные переходы синхронизируются интервалами времени фиксированной длительности, а четные - интервалами дополнительной длительности.

В соответствии с описанием в способе-прототипе время преобразования T_П=T₀(n+m)=const. Длительность T₀ задается минимально возможной (частота дискретизации - максимальна) для данной элементной базы. Следовательно, увеличить размер суммы (n+m), что однозначно снизит погрешность квантования, невозможно.

Для разрешения этого противоречия в предлагаемом способе используется тот факт, что в процессе формирования развертывающей функции принимают участие две равноправные величины - время и напряжение (в форме их произведения). Следовательно, происходит уравновешивание вольт-секундной площади S₊=(U_x+U₀)T₀ вольт-секундной площадью S_-=(U_x-U₀)T₀, а погрешность квантования определяется отклонением результата процесса уравновешивания от нулевого значения. Минимизировать значение этой площади можно, если после второго такта преобразования ввести операцию определения момента перехода через ноль с большим разрешением по времени.

Эта операция возможна, поскольку компаратор имеет быстродействие примерно на два десятичных порядка больше, чем интегратор, и это неравенство будет существовать всегда. Таким образом, длительность частного цикла преобразования может быть определена как t₀=T₀/d, где d - любое целое число от 1 до 100. Следовательно, числа m и n могут принимать следующие значения: m=[m]_T0+((m))_d, где [m]_T0 - целое значение числа m, а ((m))_d - дробная часть числа m (выражение для n аналогично). Целые значения n и m изменяются с шагом 1, т.е. 1, 2, 3, 4… (аналогично способу-прототипу), а дробные части принимают на интервале [0, 1]d равноотстоящих значений с шагом 1/d. В этом случае выражение (2) запишется в следующем виде:

Отсюда следует, что количество точек, в которых происходит полное уравновешивание, увеличивается по сравнению со способом-прототипом в d раз. Для того же примера при (n+m)=100 и d=10 получим 998 фиксированных значений, при которых может произойти полное уравновешивание процесса интегрирования, т.е. выигрыш составляет десятичный порядок. Кроме того, в остальных точках входного диапазона, где имеет место погрешность квантования, ее размер также уменьшается в d раз по сравнению с известным способом. Действительно, минимальное значение абсолютной погрешности квантования в способе-прототипе равно (U_x-U₀)T₀/Т_П, а в предлагаемом способе эта погрешность будет равна (U_x-U₀)T₀/(T_Пd). Что касается максимально возможных значений погрешностей квантования, то для рассматриваемых способов они будут равны (U_x+U₀)T₀/T_П и (U_x+U₀)T₀/(T_Пd) соответственно.

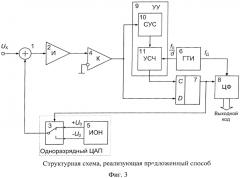
Структурная схема, реализующая предложенный способ и показанная на Фиг.3, содержит сумматор 1, интегратор 2 (И), компаратор 4 (К), триггер 7, одноразрядный ЦАП, устройство управления 9 (УУ), состоящее из схемы управления сбросом 10 (СУС) и устройства счета 11 (УСЧ). Работа схемы тактируется генератором тактовых импульсов 6 (ГТИ) частотой f₀/d, соответствующей дополнительным интервалам времени фиксированной длительности T₀/d. Ключ 3 в составе одноразрядного ЦАП осуществляет коммутацию положительного +U₀ и отрицательного -U₀ опорных напряжений, формируемых источником опорных напряжений 5 (ИОН), которые посредством сумматора складываются с входным напряжением U_x. Результат преобразования вычисляется ЦФ 8 на каждом интервале преобразования T_П, соответствующем частоте дискретизации f_Д входного сигнала, как произведение масштабирующего коэффициента и опорного напряжения. Масштабирующий коэффициент находится преобразованием выборки бинарных данных с выхода триггера 7, соответствующей текущему интервалу преобразования, как отношение разности количества логических «1» и количества логических «0» в выборке к их сумме (т.е. их общему количеству на интервале преобразования).

Временные диаграммы, поясняющие работу предлагаемого способа, приведены на Фиг.4. Развертывающая функция R(t) формируется интегратором 1 путем интегрирования суммы входного напряжения U_x с положительным +U₀ или отрицательным -U₀ опорным напряжением. Для показанной на Фиг.4 временной диаграммы интегрирование суммы входного напряжения U_x и положительного +U₀ опорного напряжения синхронизируется интервалами времени фиксированной длительности T₀, а суммы входного и отрицательного -U₀ опорного напряжения - дополнительными интервалами времени фиксированной длительности T₀/d. Формирование интервалов T₀ осуществляется устройством счета 11 путем подсчета дополнительных интервалов T₀/d. Для управления работой устройства счета 11 применяется схема управления сбросом 10, входным сигналом которой служит выходной логический уровень компаратора. Если на предыдущем фиксированном интервале времени происходит изменение полярности развертывающей функции, схема управления сбросом устанавливает коэффициент счета УСЧ, равный 1 для четных переходов (Фиг.4) и равный d для нечетных.

Из временных диаграмм видно, что предлагаемый способ для своей реализации не требует повышения характеристик аналоговой части преобразователя: интегратор, компаратор, одноразрядный ЦАП работают в тех же режимах быстродействия, что и в устройстве, реализующем способ-прототип. Выбор величины d определяется необходимым компромиссом между вычислительными возможностями цифровой части устройства и точностью преобразования.

Источники информации

1. Патент ФРГ №2214602, кл. G01R 19/26, 04.09.75.

2. Орнатский П.П. Автоматические измерения и приборы. Киев: Вища школа, 1973, с.435-437.

3. Кестер У. Аналого-цифровое преобразование. Перевод с английского под редакцией Володина Е.Б. - М.: «Техносфера», 2007. - 1016 с.

4. Шахов Э.К., Ашанин В.Н., Надев А.И. Реализация концепций ΣΔ-АЦП в интегрирующих АЦП с другими видами импульсной модуляции / Известия высших учебных заведений(поволжский регион). Пенза: ПГУ, 2006, №6. С.226-237.

5. Шахов Э.К. ΣΔ-АЦП: Процессы передискретизации, шейпинга шума квантования и децимации // Датчики и системы. - 2006 г. - №11. - с.50-57.

Способ интегрирующего аналого-цифрового преобразования, основанный на формировании интервала преобразования, состоящего из конечного числа интервалов времени фиксированной длительности, и формировании в течение каждого интервала преобразования непрерывной развертывающей функции путем интегрирования суммы или разности входного и опорного напряжений в течение каждого интервала времени фиксированной длительности, при этом результат преобразования определяют как произведение масштабирующего коэффициента и опорного напряжения, причем масштабирующий коэффициент вычисляют как отношение разности всех интервалов времени фиксированной длительности, соответствующих подключениям положительного и отрицательного опорных напряжений в течение интервала преобразования, к длительности интервала преобразования, отличающийся тем, что, с целью повышения точности, формируются дополнительные интервалы времени фиксированной длительности, причем длительность дополнительных интервалов времени фиксированной длительности задается меньше длительности интервалов времени фиксированной длительности в целое число раз, изменение полярности опорного напряжения осуществляется в момент времени, соответствующий началу текущего фиксированного интервала времени, если на предыдущем фиксированном интервале времени происходит изменение полярности развертывающей функции, причем все нечетные переходы синхронизируются интервалами времени фиксированной длительности, а четные - интервалами дополнительной длительности.