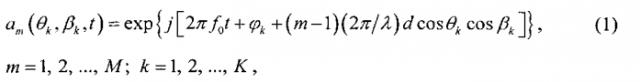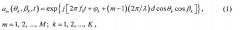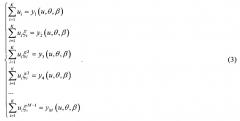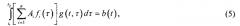Способ определения характеристик наложившихся друг на друга радиосигналов одной частоты

Способ определения характеристик наложившихся друг на друга радиосигналов одной частоты

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к радиотехнике, в частности к радиопеленгации.

Уровень техники

Пеленгация источников радиоизлучения (ИРИ) имеет место в процессе мониторинга радиоэлектронной обстановки при распространении радиоволн, сопровождающихся регистрацией наряду с исходным сигналом и отраженных сигналов от различных объектов и слоев атмосферы. Эти сигналы имеют одну частоту и регистрируются в виде суммарного сигнала. Необходимо определить для каждого зарегистрированного на одной частоте сигнала (излучаемого ИРИ и отраженных от различных объектов) азимутальный и угломестный пеленги, амплитуду и начальную фазу. Получаем задачу многосигнальной пеленгации на одной частоте. Особенностью задачи является тот факт, что зарегистрированные сигналы проходят различные расстояния.

Задача радиопеленгации является некорректной. Большинство методов многосигнальной пеленгации на одной частоте, описанных в литературе, опираются на статистические методы проверки гипотез, на метод максимума правдоподобия, сверхразрешающие методы (например, MUSIC) и др. Однако задача пеленгации ИРИ как некорректная задача не может быть решена надежно ни статистическими методами, достоверность результата которых определяется точностью полученных оценок параметров сигналов; ни МНК, в силу нелинейности и плохой обусловленности решаемой системы уравнений; ни сверхразрешающими методами, которые дают приемлемые результаты лишь при высоких соотношениях сигнал/шум и не обеспечивают разрешение ИРИ, имеющих близкие по значениям пеленги.

Все способы пеленгации имеют много общего: радиосигналы источников принимают посредством антенной системы (АС), получают комплексные амплитуды сигналов на выходах элементов антенн (вектор амплитудно-фазового распределения (АФР)) и по этим данным определяют значения параметров сигналов. Отличие состоит в том, по каким алгоритмам обрабатывают зарегистрированные антенной системой сигналы. Работ, в которых успешно решены подобные задачи, немного [1-4].

Известен авторский способ пеленгации с повышенной разрешающей способностью [1], принятый за прототип. Согласно этому способу:

1. Радиосигналы источников принимают посредством линейной антенной системы (АС), состоящей из М элементов.

2. Получают комплексные амплитуды сигналов на выходах антенн (вектор амплитудно-фазового распределения (АФР)). m-й элемент вектора АФР имеет вид y m = ∑ k = 1 K u k   e x p { j ϕ m ( θ k ,   β k ,   ϕ k ) } + n m , где K - количество источников радиосигнала (ИРИ), u_k - амплитуда сигнала k-го ИРИ, φ_m(θ_k, β_k, φ_k) - фаза сигнала k-го ИРИ на m-м вибраторе, зависящая от азимутального и угломестного пеленгов k-го ИРИ θ_k и β_k соответственно, и начальной фазы сигнала φ_k n_m - шум, имеющий место на m-м вибраторе, включающий в себя шум мирового фона и аппаратуры.

Дальше решают задачу пеленгации в следующей постановке. В эфире присутствует K ИРИ с азимутальными пеленгами θ=[θ₁, θ_{2 …} θ_K]^T, угломестными пеленгами β=[β₁, β₂ … β_K]^T и амплитудами (мощностями) излучаемых сигналов u=[u₁, u₂ … u_K]^T; y=[y₁, y₂ … y_M]^T - сигнал комплексного амплитудно-фазового распределения, описывающий амплитуды и фазы сигналов, принятых элементами АС, где М - количество элементов АС. Используемый вид модуляции (амплитудная, частотная, фазовая и др.) не имеет принципиального значения.

Для линейной антенной системы с фазовым центром, расположенным на крайнем вибраторе, элементы матрицы имеют A(θ, β, φ_k, t) вид

где

j - мнимая единица, j = − 1 ,

f₀ - частота сигналов, излучаемых пеленгуемыми ИРИ,

φ_k - начальная фаза k-го сигнала,

R - радиус окружности, вдоль которой расположены элементы антенной системы,

λ - длина волны сигналов ИРИ,

d - расстояние между соседними элементами антенной системы,

γ_i, i=1; 2; …; M - угол между линией отсчета пеленгов и линией, проведенной через центр окружности и i-й элемент антенной системы (для круговой AC),

M - количество элементов в антенной системе. Сводят задачу определения пеленгов к задаче определения показателей суммы экспонент. Данный метод приводит к оценке пеленгов посредством решения алгебраических уравнений (квадратных, кубических, четвертой степени и т.д.) путем введения новых переменных, ξ_i=1; 2; …; K. Если шаг задания этих переменных будет равномерным, то получим полное алгебраическое уравнение (линейная АС), если шаг для ξ_i будет неравномерным, то получим неполное алгебраическое уравнение или уравнение с дробными показателями (нелинейная АС). Корни полученного алгебраического уравнения - значения ξ_i.

Рассмотрим случай, когда в эфире имеют место K источников радиоизлучения (ИРИ). Выход m-го элемента линейной АС имеет вид

где

u_i - амплитуда i-го сигнала на m-ом вибраторе.

Введем обозначение ξ_i=exp(j(2π/λ)dcosθ_icosβ_iφ_i), i=1; 2; …; K. Тогда можно записать следующую систему уравнений

В процессе решения системы (3) определяют ξ_i, а затем u, θ, β, φ.

Корни ξ_i полученного полинома можно записать как функции от случайных величин C_i, i=0; 1; …; K-1, и вычислить дисперсии значений корней как для функций случайных аргументов.

Способ-прототип обладает следующими недостатками:

- способ-прототип предназначен для линейных АС; определить с помощью линейных АС угломестный пеленг β нельзя;

- алгоритм прототипа не учитывает временные задержки отраженных сигналов;

- для нелинейных и круговой АС не удается свести задачу к системе алгебраических уравнений, в которых неизвестные переменные имеют целочисленные показатели степени;

- нельзя исключить неизвестные амплитуды сигналов на первом этапе решения задачи, тем самым раздельно определить амплитуды сигналов и пеленги излучателей.

Указанные недостатки не позволяют применять способ-прототип в реальных условиях, когда регистрируются одновременно и отраженные сигналы.

Раскрытие изобретения

Предлагаемый способ свободен от указанных недостатков и является параметрическим способом многосигнального пеленгования на одной частоте.

Достигаемый технический результат - уменьшение времени и повышение точности определения пеленгов при приеме радиосигналов источника радиоизлучения с использованием антенных систем (АС), состоящих из слабонаправленных элементов (вибраторов), а также получение интервальных оценок пеленгов. Повышение скорости пеленгации и повышение достигается за счет использования эффективного алгоритма идентификации параметров радиосигналов.

Способ определения характеристик наложившихся друг на друга радиосигналов одной частоты, а именно: амплитуды, азимутального и угломестного пеленгов источника радиоизлучения и начальной фазы φ₀ его сигнала при регистрации основного и отраженных сигналов, включает в себя прием этого многолучевого сигнала антенной системой (АС), состоящей из M элементов, формируют ансамбль сигналов o ˙ m ( t ) , m=1; 2; …; M, зависящих от времени t, синхронно преобразуют ансамбль принятых сигналов o ˙ m ( t ) в цифровые сигналы o ˙ m ( z ) , где z - номер временного отсчета сигнала, преобразуют цифровые сигналы o ˙ m ( z ) в сигнал комплексного амплитудно-фазового распределения (АФР), описывающий амплитуды и фазы сигналов, принятых элементами АС, восстанавливают вектор комплексных амплитуд сигналов y=[y₁ y₂ … y_M]^T, полученных с выхода каждого элемента АС. При этом на каждом элементе АС во временном пространстве зарегистрированный сигнал подвергается преобразованию Фурье, получают модуль этого преобразования, модуль преобразования Фурье от ожидаемой формы единичного сигнала и от импульсной характеристики трассы, по которой проходил сигнал, определяют модуль преобразования Фурье функции, описывающей смещение сигналов, поделив модуль преобразования Фурье сигнала, полученного с выхода элемента АС, на произведение модулей преобразования Фурье от ожидаемой формы единичного сигнала и от импульсной характеристики трассы, по которой проходил сигнал, исследуют зависимость от частоты модуля преобразования Фурье функции, описывающей смещение сигналов, по точкам минимумов которой определяют разность по времени поступления сигналов, а по точкам максимумов и минимумов - амплитуды или относительные амплитуды сигналов; по известным временным значениям разности прихода сигналов и по известной частоте определяют аналитическое выражение для первого сигнала и его амплитуду и фазу, вычитают первый сигнал из суммарного сигнала, повторяют последнюю процедуру до тех пор, пока не определят амплитуды и фазы каждого сигнала в суммарном сигнале, по известным фазам одного сигнала на разных элементах АС определяют азимутальный и угломестный пеленги и начальную фазу каждого сигнала.

Способ также обычно дополнительно включает вычисление дисперсий значений амплитуды, азимутального и угломестного пеленгов и начальной фазы сигнала источника радиоизлучения по общей формуле: D ( f ( x ) ) = ∑ [ ∂ f ( x ) ∂ ( x i ) ] 2 D ( x i ) , где f(x) - функция, определяющая значение искомого параметра; x_i - i-я переменная, входящая в f(x_i), i=1, 2, …, k, k - число переменных; с использованием аналитических выражений частных производных ∂ f ( x ) ∂ x i и заранее известных величин дисперсий D(x_i) переменных x_i, в данном случае в качестве f(x) выступают формулы для cosβ, tgθ, φ₀, а в качестве x_i выступают все другие переменные, входящие в формулу, а именно: c o s β = P 1 − ϕ 0 c o s θ ; тогда f(x)=cosβ, P₁≡x₁; φ₀≡x₂; cosθ≡x₃. и D ( c o s β ) = ∑ i = 1 3 ( ∂ cos β ∂ x i ) 2 D ( x i ) .

Перечень чертежей

Фиг.1. Определение интервалов между двумя импульсами: а, б - выходные сигналы; в - импульсная характеристика системы; г - квадраты модулей Фурье-образов выходных сигналов.

Фиг.2. Влияние неопределенности исходных данных на квадрат модуля Фурье-образа выходного сигнала.

Фиг.3. Неразрешенные импульсы: 1 - суммарный; 2 - единичный.

Фиг.4. Функция |I(ω)| для импульса, приведенного на фиг.3.

Осуществление изобретения

Сигналы рассматриваются как детерминированные, подверженные аддитивной помехе, оценки параметров которых подлежат определению. В качестве примера нелинейной АС рассматривается круговая АС, состоящая из нескольких слабонаправленных элементов (вибраторов). В качестве фазового центра (точки, относительно которой происходит измерение фаз сигналов, приходящих на элементы антенной системы) выбирается один из вибраторов.

Ставится задача определения следующих параметров для присутствующего в эфире ИРИ:

- временные задержки зарегистрированных сигналов;

- амплитуды (мощности) зарегистрированных сигналов;

- азимутальные и угломестные пеленги каждого зарегистрированного сигнала;

- начальные фазы каждого зарегистрированного сигнала.

Поскольку на результаты измерений неизбежно накладывается помеха, а также имеют место ошибки измерений, обусловленные используемой аппаратурой, необходимо получить не только точечные оценки искомых параметров, но и их ковариационные матрицы или, по крайней мере, дисперсии.

В предлагаемом способе с помощью преобразования Фурье определяются отдельно на КАЖДОМ элементе АС амплитуды сигналов, разности по времени прихода сигналов и затем значения фаз наложившихся сигналов. Принципиально важно точно знать временной интервал между приходом сигналов, т.е. правильно последовательно выделить запись каждого сигнала, начиная с пришедшего первым. Примем во внимание следующий важный факт. Поскольку сигналы имеют одну частоту, но разные время прихода и пеленги и, соответственно, разные начальные фазы, то их можно рассматривать как результат смешения во времени второго сигнала относительно первого и т.д. А смешение сигналов во времени позволяет последовательно выделить зарегистрированные сигналы, фазы которых определяются соответствующими пеленгами сигналов и начальными фазами сигналов. Но необходимо точно определять временные задержки сигналов. Проблема определения временных сигналов состоит в том, что и исходный сигнал, и регистрируемый суммарный сигнал - это гармонические сигналы на одной частоте, но с возможно разными амплитудами и фазами, которые определяются амплитудами и фазами наложившихся сигналов. А эти величины неизвестны - их надо определить.

Тот факт, что каждый элемент АС обрабатывается независимо, позволяет сократить число элементов АС пеленгатора, но их должно быть не менее трех, чтобы определить пеленги и начальную фазу сигналов. В реальной практике наиболее часто рассматриваются случаи наложения двух и трех сигналов.

Для классических линейных АС нельзя определить угол места, для нелинейных АС набеги фаз различны на каждом элементе АС. Поэтому будем рассматривать временную запись суммарного сигнала на каждом элементе АС.

Выход m-го элемента нелинейной АС имеет вид

где A_i - амплитуда i-го сигнала;

f_i(t) - гармонические сигналы с одной частотой, но с разными фазами;

b_m - суммарный сигнал на m-ом элементе АС.

Если излучение в процессе прохождения подвергается влиянию среды и регистрирующей (передающей) системы с импульсной характеристикой g(t), то суммарная линия b(7) описывается интегральным уравнением

Применив преобразование Фурье к уравнению (5), или соответственно к уравнению (4), получим [5-7]

где |F(ω)|, |G(ω)| и |B(ω)| - соответственно модули Фурье-образов ∑ i = 1 n A i f i ( t ) ; g(t)и b(t).

Смещение импульсов f_i(t) позволяет записать |F(ω)| в виде произведения

Здесь |Φ(ω)| - модуль Фурье-образа f(t); |I(ω)| - модуль сомножителя, описывающего смещение.

Согласно (6)

и в то же время по теореме смещения [5]

где τ_j - временной интервал между первым и j-ым импульсами серии; τ₀=0.

Из формулы (9) следует, что спектр |I(ω)| отличается при разном числе поступивших сигналов, т.е. можно сразу определить число поступивших сигналов.

Модули |Φ(ω)| и |G(ω)| определяют в процессе калибровки при обработке результатов. Менее точно можно получить |Φ(ω)| |G(ω)| как огибающую функции |F(ω)|, например, построив линию регрессии по максимумам функции |F(ω)|. Частоты, при которых |Φ(ω)| |G(ω)|=0, не рассматриваются. Таким образом, значения |I(ω)| рассчитываются по условию (8), а с другой стороны, они известны из формулы (9). Таким образом, если форма каждой компоненты неразрешенной линии описывается одной и той же функцией, то веса A_j компонент неразрешенных линий и интервалы τ_j, на которые сметены компоненты относительно друг друга, находятся из условия

Выделив частоты гармоник в |I(ω)|, при которых наблюдаются максимумы и минимумы |I(ω)|, и, определив их амплитуды, находим оценки искомых параметров A_j и τ_j.

В процессе обработки данных функции f(t) и b(t) задаются набором дискретных значений с шагом h. Погрешность вычисления |I(ω)| в основном определяется погрешностью |B(ω)|; значения f(t) и g(t) и соответственно |Φ(ω)| и |G(ω)| и могут быть получены при калибровке с требующейся точностью. Кроме того, |G(ω)| и |Φ(ω)| - достаточно пологие функции в области частот, представляющих интерес, и большой ошибки они не внесут.

Реализация алгоритма изобретения.

1. Принимают многолучевой сигнал антенной системой (АС), состоящей из M элементов, и формируют ансамбль сигналов o ˙ m ( t ) , m=1; 2; …; M, зависящих от времени t.

2. Синхронно преобразуют ансамбль принятых сигналов o ˙ m ( t ) в цифровые сигналы o ˙ m ( z ) , где z - номер временного отсчета сигнала.

3. Преобразуют цифровые сигналы o ˙ m ( z ) в сигнал комплексного амплитудно-фазового распределения (АФР), описывающий амплитуды и фазы сигналов, принятых элементами АС. Восстанавливается вектор комплексных амплитуд сигналов y=[y₁ y₂ … y_M]^T, полученных с выхода каждого элемента АС.

4. На каждом элементе АС во временном пространстве выделяется сигнал для обработки, в котором получают модуль преобразования Фурье. Получают также модуль преобразования Фурье от ожидаемой формы единичного сигнала и от импульсной характеристики трассы, если есть необходимость учесть влияние трассы, по которой проходил сигнал.

5. Определяют модуль преобразования Фурье функции, описывающей смещение сигналов, поделив модуль преобразования Фурье выделенного суммарного сигнала, полученного с выхода каждого элемента АС, на произведение модулей преобразования Фурье от ожидаемой формы единичного сигнала и от импульсной характеристики трассы, по которой проходил сигнал.

6. Исследуют зависимость от частоты модуля преобразования Фурье функции, описывающей смещение сигналов. По точкам минимумов определяют разность времен прихода сигналов, а по точкам максимумов и минимумов - амплитуды или относительные амплитуды сигналов.

7. По известным значениям разности времен прихода сигналов выделяют первый сигнал и традиционными методами находят его аналитическое выражение, по которому определяют его амплитуду и фазу. После выделения первого сигнала выделяют второй и т.д. По известным аналитическим выражениям для каждого сигнала определяют амплитуды и фазы каждого сигнала в суммарном сигнале.

8. По известным фазам составляется система алгебраических уравнений, из которой определяют азимутальный и угломестный пеленги и начальную фазу каждого сигнала.

9. Поскольку азимутальный и угломестный пеленги и начальная фаза каждого сигнала описываются аналитическими выражениями, то их дисперсии определяются как дисперсии функции со случайными аргументами.

Определение разности времени прихода сигналов

Рассмотрим алгоритм для наиболее частого случая, когда зарегистрированный сигнал состоит из двух импульсов, имеющих одинаковую форму, но разные амплитуды A₁ и A₂, и отстоящих друг от друга на интервал τ (наложение отраженных сигналов). В этом случае |I²(τ, A₁, A₂, ω)| определяется формулой

Оценку интервала времени между импульсами τ и оценки амплитуд A₁, A₂ наиболее просто можно произвести по точкам экстремумов кривой |I(ω)|: точки минимума соответствуют

а точки максимума -

Из условия (11) находят оценки интервала времени между импульсами, а из условий (11) и (12) находят оценки амплитуд (или отношение амплитуд при заметном влиянии неизвестной функции g(t)) импульсов - получают из системы уравнений

Порядок следования импульсов в данном случае проще всего определять по форме суммарного импульса. При числе импульсов m>2 эта неопределенность устраняется.

Поскольку нам известна частота регистрируемых сигналов, и мы определили время смещения второго сигнала относительно первого, достаточно просто определить традиционными методами [5-7] уравнение для первого сигнала. Вычитаем первый сигнал из суммарного и определяем необходимые характеристики обоих сигналов раздельно.

В силу того, что в практических задачах функции |G(ω)| и |Φ(ω)| достаточно пологие, можно найти качественные оценки интервала τ и отношения амплитуд A₁ и A₂ даже при неизвестном значении произведения |G(ω)| |Φ(ω)|, даже если функции g(t) и f(t) неизвестны.

Методом статистического моделирования установлено, что относительная погрешность исходных данных переносится на значения амплитуд двух сигналов с коэффициентом порядка 1, а на значения интервалов - с коэффициентами меньше единицы.

Пример 1: sin 785t+sin (785t+π/2)=b_m; круговая частота ω=785; период = 8·10^-3 сек; принимаем в рассмотрение только положительные значения каждой функции. Сигнал записан в течение 10^-2 сек, смещение сигналов составляет 2×10^-3 сек. Амплитуды сигналов равны единице.

Преобразование Фурье в данном случае имеет вид

Вычисляя этот интеграл как сумму двух интегралов, увидим, что второй интеграл отличается от первого множителем e x p ( − i ω π 2 × 7 8 5 ) . Точка минимума будет при условии 2 π f π 2 × 785 = π . Изменяя частоту в окрестности f, получили |I²(ω)|=0 при частоте 250 Гц, т.е. амплитуды сигналов одинаковы. Отсюда смещение τ=2·10^-3 сек. Из условия A 1 + A 2 = I ( 2 π τ ) = 2 следует, что амплитуды сигналов равны единице. В результате получили смещение по времени между сигналами.

Определение пеленгов и начальной фазы сигналов. Поскольку мы определили уравнения каждого сигнала, то нам известны и значения фаз сигналов. Приступим к определению пеленгов и начальной фазы сигналов. Для этого АС должна содержать не менее трех элементов, не параллельных друг другу. Для каждого сигнала на каждом элементе АС определяем свои значения фаз и записываем для каждой фазы свои уравнения, из которых находим значения пеленгов и начальных фаз сигналов. Для каждой фазы r_m получим следующую систему уравнений

r m = 2 π P λ cos ( θ − γ m ) cos β + ϕ 0 , m=1, …, n; или:

p m = cos ( θ − γ m ) cos β + ϕ ⌢ ; где p m = r m λ 2 π R ; ϕ ⌢ 0 = ϕ 0 λ 2 π R ; γ₁=0 - начало отсчета углов γ_m.

Составим систему уравнений для пеленгов θ, β и начальной фазы сигнала ϕ ⌢ 0 :

Решить эту систему можно разными методами. Приведем один из них. Переносим ϕ ⌢ 0 вправо, делим все уравнения на первое. Получим

или в матричном виде: A θ → = Y , где

Отсюда решение

Формула (15) - это матричная формула для tgθ и φ₀. Компьютеру задают формулы (15), а компьютер выдает 2 числа: значения t g θ ( P 1 − ϕ ⌢ 0 ) = a 1 и φ₀=a₂. Тогда t g θ = a 1 P 1 − ϕ ⌢ 0 и φ₀=a₂; c o s β = P 1 − ϕ 0 c o s θ .

После нахождения пеленга θ и начальной фазы φ₀ определяют пеленг β.

Из-за простоты вычислений значительно уменьшается время вычислений и увеличивается точность определения пеленгов. Кроме того, точность определения пеленгов повышается, поскольку учтена величина φ₀, которая входит в набег фаз и влияет на значения пеленгов.

Следует отметить, что операции, имеющие место в формулах (14) и (15), не представляют большой вычислительной сложности и, соответственно, требуют малых временных затрат.

Что касается повышения достоверности результатов, поскольку получены формулы для искомых величин, то их дисперсии определяют, как для функций от случайных аргументов [8]. Вычисление дисперсий значений амплитуды, азимутального и угломестного пеленгов и начальной фазы сигнала источника радиоизлучения проводится по общей формуле: D ( f ( x ) ) = ∑ [ ∂ f ( x ) ∂ x i ] 2 D ( x i ) , где f(x) - функция, определяющая значение искомого параметра; x_i - i-я переменная, входящая в f(x_i), i=1, 2, …, k, k - число переменных; с использованием аналитических выражений частных производных ∂ f ( x ) ∂ x i и заранее известных величин дисперсий D(x_i) переменных x_i, в данном случае в качестве f(x) выступают формулы для cosβ, tgθ, φ₀, а в качестве x_i выступают все другие переменные, входящие в формулу, а именно: c o s     β = P 1 − ϕ 0 c o s θ ; тогда f(x)=cosβ, P₁≡x₁; φ₀≡x₂; cosθ≡x₃ и D ( c o s β ) = ∑ i = 1 3 ( ∂ cos β ∂ x i ) 2 D ( x i ) .

Можно пропустить операцию определения значений фаз, а сразу записать систему уравнений для найденного значения разности фаз. Тогда составляется и решается только одна система уравнений, но более громоздкая.

Пример 2. Рассмотрим случай двух сигналов. Исходные данные - зарегистрированные сигналы, каждый из которых является суммой двух импульсов, приведены на фиг.1, а, б. На том же чертеже приводится предполагаемая ориентировочная импульсная характеристика системы, через которую прошли анализируемые сигналы (фиг.1, в). Требуется по этим исходным данным в каждом случае определить интервал между импульсами и отношение их амплитуд.

На фиг.1, г приведены квадраты модулей Фурье-образов первого (кривая 1) и второго (кривая 2) сигналов. Из анализа Фурье-образов следует, что временной интервал между компонентами первого импульса составляет 5·10^-6 с, а второго - 7·10^-6 с. В первом случае амплитуды компонент одинаковы, а во втором - достаточно близки.

Для определения погрешности оценки временных интервалов между импульсами за счет неопределенности амплитуды зарегистрированного сигнала были проведены статистические испытания: амплитуды сигналов с помощью датчика случайных чисел, подчиняющихся нормальному закону, изменялись в пределах ±5% при доверительной вероятности 68%. Погрешность в определении временных интервалов между компонентами импульсов оказалась равной ±4% при той же доверительной вероятности.

Пример 3. На фиг.2 приведен квадрат модуля Фурье-образа |B(ω)|² выходного сигнала для последовательности пяти треугольных импульсов одинаковой формы и амплитуды, отстоящих друг от друга на 250 нс. Длительность каждого импульса по основанию равна 250 нс. Имитировалось прохождение этой серии импульсов через отрезок радиокабеля марки РК-75-9-13 длиной 3 км. Принималось, что амплитуды импульсов - нормально-распределенные случайные величины с относительным среднеквадратическим отклонением, равным 5%. На фиг.2 показаны огибающие возможных отклонений в значениях квадратов Фурье-образов. Положение нулей практически не изменилось. Первый нуль получен при частоте f=0,816 МГц, что соответствует интервалу между импульсами, равному 250 нс.

Пример 4. Рассмотрим обработку суммарного импульса, три компоненты которого имеют длительность по основанию 40 единиц и две последние смещены соответственно от первой компоненты на пять и восемь единиц (фиг.3). Точность исходных данных - не хуже 2%.

Вид функции |I(ω)| для приведенного импульса показан на фиг.4. Значения |I(ω)| получены для ω∈[0; 2, 5] с шагом Δω=π²/160. При выбранном шаге Δω получены следующие оценки интервалов: τ₁=4,92±0,13; τ₂=7,94±0,16; τ₂-τ₁=3,0±0,1.

При найденных оценках τ₁ и τ₂ методом наименьших квадратов установлено, что компоненты суммарного импульса имели равные амплитуды.

При больших погрешностях исходных данных для оценки точности получаемых результатов предпочтительнее метод статистических испытаний, так как исходные данные подвергаются в описанном способе целому ряду нелинейных преобразований.

Источники информации

1. Грешилов А.А. RU, патент, 2380719 С2, МПК G01S 5/04 (2006.01), 2008 г.

2. Патент RU 2380720, опубликовано 27.01.2010, МПК G01S 5/04.

3. Патент RU 2151406, опубликовано 20.06.2000, МПК G01S 5/04, G01S 5/14, H04B 17/00.

4. Грешилов А.А., Плохута П.А. Патент RU 2382379, МПК G01S 5/04, опубл. 20.02.2010.

5. Г. Деч. Руководство к практическому применению преобразования Лапласа и Z-преобразования. Перевод с немецкого. - М.: Наука. - 1971.

6. Грешилов А.А. Некорректные задачи цифровой обработки информации и сигналов. - М.: Изд. Логос - 2009.

7. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. - М.: Наука. - 1980.

8. Грешилов А.А. Математические методы принятия решений: Учебное пособие для вузов. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. - 584 с.

Способ определения характеристик наложившихся друг на друга радиосигналов одной частоты, а именно: амплитуды, азимутального и угломестного пеленгов источника радиоизлучения и начальной фазы φ₀ его сигнала при регистрации основного и отраженных сигналов, включающий в себя прием этого многолучевого сигнала антенной системой (АС), состоящей из М элементов, формируют ансамбль сигналов ó_m(t), m=1; 2;…;М, зависящих от времени t, синхронно преобразуют ансамбль принятых сигналов ó_m(t) в цифровые сигналы ó_m(z), где z - номер временного отсчета сигнала, преобразуют цифровые сигналы ó_m(z) в сигнал комплексного амплитудно-фазового распределения (АФР), описывающий амплитуды и фазы сигналов, принятых элементами АС, восстанавливают вектор комплексных амплитуд сигналов y=[y₁ y₂…y_M]^T, полученных с выхода каждого элемента АС, отличающийся тем, что на каждом элементе АС получают и выделяют суммарный сигнал, который подвергается преобразованию Фурье, получают модуль этого преобразования, модуль преобразования Фурье от ожидаемой формы единичного сигнала и от импульсной характеристики трассы, по которой проходил сигнал, определяют модуль преобразования Фурье функции, описывающей смещение сигналов, поделив модуль преобразования Фурье сигнала, полученного с выхода элемента АС, на произведение модулей преобразования Фурье от ожидаемой формы единичного сигнала и от импульсной характеристики трассы, по которой проходил сигнал, получают зависимость от частоты модуля преобразования Фурье функции, описывающей смещение сигналов, по точкам минимумов которой определяют разность во времени поступления сигналов, а по точкам максимумов и минимумов - амплитуды или относительные амплитуды сигналов; по полученным временным значениям разности прихода сигналов и по известной частоте регистрируемых сигналов выделяют первый сигнал, определяют его амплитуду и фазу, вычитают первый сигнал из с