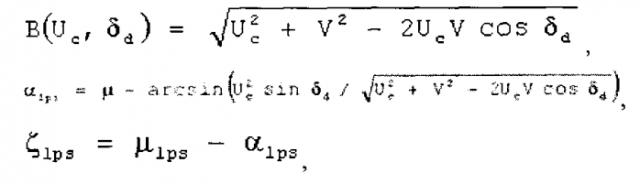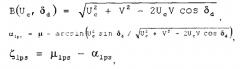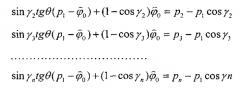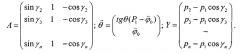Способ определения координат источника радиоизлучения

Способ определения координат источника радиоизлучения

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к радиотехнике, в частности к радиопеленгации.

Уровень техники

Пеленгация источников радиоизлучения (ИРИ) имеет место в процессе мониторинга радиоэлектронной обстановки. При этом необходимо определять азимутальные, угломестные пеленги ИРИ и амплитуду сигнала, по которым определяют координаты источника радиоизлучения. Пеленгатор регистрирует излучение путем записи сигналов на элементах антенной системы АС, на вибраторах. Выполняя различные действия над сигналами с вибраторов, определяют параметры излучения, а затем - координаты источника радиоизлучения. Проблема состоит в том, какие действия над сигналами окажутся более эффективными.

Имеются патенты, посвященные данной проблеме. В качестве прототипа выбран патент RU 2419106 Способ и устройство определения координат источника радиоизлучения (МПК G01S 13/46, опубл. 20.05.2011), как наиболее полно рассматривающий проблему. В прототипе поставленная цель достигается тем, что в способе определения координат источника радиоизлучения, включающем прием сигналов ИРИ в заданной полосе частот ΔF перемещающимся в пространстве бортовым пеленгатором на летно-подъемном средстве (ЛПС), измерение пространственно-информационных параметров обнаруженных сигналов: азимута θ_i и угла места β_i в системе координат антенной системы с одновременным определением местоположения ЛПС {B_lps, L_lps, H_lps}, где B_lps, L_lps и H_lps соответственно широта, долгота и высота ЛПС, предварительное определение удаления ИРИ от ЛПС d_i и координат ИРИ в момент времени t_i V П i → = { X 0 , Y 0 , Z 0 } i в левосторонней системе декартовых координат антенной системы пеленгатора, корректируют координаты ИРИ V Y i → = { X 0 ' , Y 0 ' , Z 0 ' } i с учетом априорно известной ориентации антенной системы бортового пеленгатора относительно ЛПС {k_ant, l_ant, ζ_ant} путем последовательного умножения значений координат V П i → на соответствующие углам Эйлера матрицы поворота. После чего определяют истинные геоцентрические координаты местоположения ИРИ V Г Ц i → = { X 0 ' ' , Y 0 ' ' , Z 0 ' ' } i с учетом измеренных в момент времени t_i пространственных углов ЛПС: крена k_lpsi, тангажа l_lpsi, курсового угла α_lpsi и склонения ζ_lpsi, а также координат его местоположения: широты B_lpsi, долготы L_lpsi, и высоты H_lpsi, а склонение ζ_lpsi определяют как разность между путевым µ_lpsi и курсовым α_lpsi углами ЛПС. Преобразуют истинные геоцентрические координаты V Г Ц i → местоположения ИРИ в географические координаты V Г i → = { B 0 , L 0 , H 0 } i . При этом для определения курсового угла летно-подъемного средства принимают радиосигналы от космических аппаратов (КА) глобальных навигационных спутниковых систем (ГНСС), выделяют из обнаруженных сигналов навигационные сообщения КА ГНСС и осуществляют их демодуляцию, оценивают навигационные параметры и рассчитывают массив из I векторов состояния ЛПС W i → ( B l p s i , L l p s i , H l p s i , V X i , V Y i , V Z i , t i ) , где V_Xi, V_Yi, V_Zi - величины, описывающие вектор V → и характеризующие значение путевого угла µ_i и путевой скорости V_i ЛПС, i=10, 11, ^…, I, а емкость массива I определяют заданной точностью измерения курсового угла α_lpsi. В зависимости от геометрии маршрута полета ЛПС оценивают значения воздушных скоростей ЛПС B ˙ 1 ( U , δ ) , B ˙ 2 ( U , δ ) , …, B ˙ 1 ( U , δ ) для соответствующих значений вектора состояния W i → ( B l p s i , L l p s i , H l p s i , V X i , V Y i , V Z i , t i ) в соответствии с выражением B ˙ l ( U l , δ k ) = ( V i sin μ i − U l sin δ k ) 2 + ( V i cos μ i − U l cos δ k ) 2 ,), курсового угла α_lpsi и склонения ζ_lpsi в соответствии с выражениями: B ( U c , δ d ) = U c 2 + V 2 − 2 U c V cos δ d , ζ_lps=µ_lps-α_lps, а найденные параметры ветра U_c и δ_d используют в очередном цикле измерений курсового угла α_lps и склонения ζ_lps в качестве средних значений U ¯ и δ ¯ ограниченных выборок {U} и {δ} оценочных параметров ветра. α l p s = μ − arcsin ( U c 2 sin δ 4 / U c 2 + V 2 − 2 U c V cos δ d ) .

В прототипе достигается более полный учет пространственной ориентации ЛПС (а следовательно, и антенной системы пеленгатора), что и обуславливает положительный эффект в виде повышения точности местоопределения ИРИ. Перечисленная совокупность существенных признаков позволяет повысить точность местоопределения ИРИ за счет более полного и объективного измерения пространственных параметров ЛПС (угла ориентации антенной решетки измерителя) в условиях воздействия на него возмущающих факторов (ветровой нагрузки, выполнения маневров ЛПС и др.).

При этом для определения курсового угла летно-подъемного средства принимают радиосигналы от космических аппаратов (КА) глобальных навигационных спутниковых систем (ГНСС) и рассчитывают массив из I векторов состояния ЛПС W i → ( B l p s i , L l p s i , H l p s i , V X i , V Y i , V Z i , t i ) , где V_Xi, V_Yi, V_Zi - величины, описывающие вектор V → и характеризующие значение путевого угла µ_i и путевой скорости V_i ЛПС, i=10, 11, ^…, I, а емкость массива I определяют заданной точностью измерения курсового угла α_lpsi. В зависимости от геометрии маршрута полета ЛПС оценивают значения воздушных скоростей ЛПС B ˙ 1 ( U , δ ) , B ˙ 2 ( U , δ ) , …, B ˙ 1 ( U , δ ) для соответствующих значений вектора состояния W i → ( B l p s i , L l p s i , H l p s i , V X i , V Y i , V Z i , t i ) в соответствии с выражением

B ˙ l ( U l , δ k ) = ( V i sin μ i − U l sin δ k ) 2 + ( V i cos μ i − U l cos δ k ) 2 .

где V_i - i-e значение путевой скорости, µ_i - i-e значение путевого угла, U_l - 1-е оценочное, значение скорости ветра, l=1, 2, ^…, L, δ_k - k-e оценочное направление ветра, k=1, 2, ^…, K, оценивают качество принятого решения о параметрах ветра в соответствии с выражением f ( U l , δ k ) = max B ˙ s ( U l , δ k ) − min B ˙ m ( U l , δ k ) , где max B ˙ s ( U l , δ k ) и min B ˙ m ( U l , δ k ) соответственно максимальное и минимальное оценочные значения воздушных скоростей из набора { B ˙ l ( U l , δ k ) , B ˙ 2 ( U l , δ k ) , …, B ˙ I ( U l , δ k ) } для параметров ветра U_l и δ_k, результаты вычислений f(U_l,δ_k) сравнивают с пороговым значением f_зад(U,δ), определяющим априорно заданную точность оценивания параметров ветра U и δ, при невыполнении пороговых условий параметрам ветра U и δ присваивают очередные значения и повторяют процедуру вычисления набора оценочных значений воздушных скоростей, при выполнении на очередной итерации пороговых условий f_зад(U,δ) за параметры ветра принимают соответствующие значения U_c и δ_d, на основе навигационного треугольника скоростей рассчитывают значения воздушной скорости B(U_c,δ_d), курсового угла α_lps и склонения ζ_lps в соответствии с выражениями:

а найденные параметры ветра U_c и δ_d используют в очередном цикле измерении курсового угла α_lps и склонения ζ_lps в качестве средних значений U ¯ и δ ¯ ограниченных выборок {U} и {δ} оценочных параметров ветра. С помощью внешнего генератора проводится с шагом Δθ и Δβ измерение фаз на элементах АС, которые запоминаются и служат в дальнейшем для определения пространственно-информационных параметров обнаруженных сигналов: азимута θ_i и угла места β_i.

Изобретение-прототип имеет недостатки.

Определение пеленгов с помощью заранее подготовленной таблицы, связывающей показания на элементах АС с азимутальными и угловыми пеленгами, полученными с помощью внешнего генератора, включая облет ЛПС, не обеспечит высокой точности результатов.

Основное назначение блоков 12, 13, 14, 15, 16 и 2, 3 в устройстве, реализующем прототип, состоит в том, чтобы оценить степень отличия измеренных параметров Δϕ_l,h,изм (f_v) от эталонных значений Δϕ_l,h,эт (f_v), рассчитанных для всех направлений прихода сигнала Δθ_k и Δβ_c и всех f_v используют формулу

Но в этой формуле нет никакой информации о погрешностях участвующих величин.

Нет четкого алгоритма определения погрешностей координат источника излучения.

В изобретении проводится много математических операций с измеренными величинами (случайными величинами). Ошибки при каждой математической операции накапливаются, но авторы не уделяют этому внимания.

Раскрытие изобретения

Предлагаемый способ учитывает указанные недостатки.

Способ определения координат источника радиоизлучения (ИРИ) заключается в том, что принимают сигналы ИРИ в заданной полосе частот ΔF наземным или перемещающимся в пространстве бортовым пеленгатором, установленным на летно-подъемном средстве (ЛПС), измеряют пространственно-информационные параметры обнаруженных сигналов: азимут θ, угол места β и начальные фазы сигналов в прямоугольной декартовой системе координат с одновременным определением местоположения ЛПС, корректируют координаты ИРИ с учетом априорно известной ориентации антенной системы бортового пеленгатора относительно ЛПС, после чего вычисляют истинные геоцентрические координаты местоположения ИРИ с учетом измеренных пространственных углов ЛПС, для определения курсового угла летно-подъемного средства (ЛПС) принимают радиосигналы от космических аппаратов (КА) глобальных навигационных спутниковых систем (ГНСС). При этом с каждого пеленгующего устройства измеренные комплексные амплитуды с каждого элемента АС и функция, описывающая комплексную огибающую выходов элементов АС, поступают в блок логарифмирования, затем в блок сравнения действительных и мнимых частей аналитического выражения натурального логарифма комплексной огибающей выходов элементов АС и натурального логарифма измеренных комплексных амплитуд сигналов с каждого элемента АС, получают амплитуду сигнала и систему уравнений для определения по явным формулам, описывающим точечные оценки пространственно-информационных параметров обнаруженных сигналов: азимут θ, угол места β, начальную фазу сигнала и их погрешности, которые поступают в вычислитель 1 для определения корреляционной матрицы полученных оценок, как от функции случайных аргументов, затем в базу пеленгов ИРИ и их погрешностей наряду с подобной информацией от других пеленгующих устройств, на основе данных базы пеленгов формируются системы уравнений из первых частных производных от функционала ортогональной регрессии, позволяющего учесть погрешности всех исходных данных, по координатам ИРИ для прямых линий в пространстве и на плоскости, по которым в вычислителях 2 и 3 определяются точечные оценки координат ИРИ в пространстве и на плоскости, с помощью обратной матрицы, составленной из отрицательных значений всех вторых частных производных от функционала ортогональной регрессии по координатам ИРИ в вычислителях 4 и 5 определяются ковариационные матрицы оценок координат ИРИ.

Выбор вида прямых - на плоскости или в пространстве по признаку: если ИРИ в воздухе, то прямая линия в пространстве, а если на земле - прямая линия на плоскости.

Чтобы определить координаты ИРИ, надо знать координаты регистратора (пеленгатора). И тот и другой могут быть на земле и в воздухе (например, беспилотники). В предлагаемом способе они не разделяются. Координаты пеленгаторов могут определяться разными способами, в том числе и ГНСС. Эти координаты известны.

Пеленгаторов нужно два и более. Случайная компонента погрешности результата уменьшается пропорционально корню из числа пеленгаторов при приблизительно близких погрешностях в каждом случае. Иначе надо учесть погрешность каждого со своим весом.

В сравнении с прототипом предлагаемый способ лучше по быстродействию (в предлагаемом способе - по формуле, а в прототипе облетают объект) и точности не менее двух раз. По точности - здесь есть и принципиальный момент: никто не учитывает погрешности всех исходных данных (учитывают только одной величины!), т.е. попадают "сбоку". Отсюда же следует и резкое снижение стоимости затрат и оборудования на реализацию предлагаемого способа.

В реализации алгоритма, прежде всего, определяется заранее ф-я комплексной огибающей выходов элементов АС для каждой АС. Для стандартных видов (линейная, круговая) функции известны. Если другой вид, то его сводят к известному, часто к линейной АС. К линейной АС даже сводят и круговую АС. Посмотрев на АС и вспомнив, в каком случае Вы можете получить пеленг, к этому случаю и сводим конкретную АС. Это делается один раз и навсегда заранее.

Фиг.1. Блок-схема алгоритма определение координат ИРИ

Осуществление изобретения

На фиг.1 обозначены позициями:

1. Пеленгующие устройства

2. Комплексные амплитуды с выходов элементов АС

3. Комплексная огибающая выходов элементов АС

4. Блок логарифмирования

5. Блок сравнения действительных и мнимых частей

6. Амплитуда зарегистрированного сигнала

7. Формирование уравнений из равенства мнимых частей

8. Решатель систем алгебраических уравнений

9. Точечные оценки пеленгов и начальной фазы сигнала

10. Вычислитель 1. Вычисление ковариционной матрицы оценок пеленгов и начальной фазы сигнала

11. База пеленгов и их погрешностей

12. Выбор: прямая линия - в пространстве или на плоскости

13. Формирование системы уравнений для прямой на плоскости

14. Формирование системы уравнений для прямой в пространстве

15. Вычислитель 2. Точечные оценки координат ИРИ на плоскости

16. Вычислитель 3. Точечные оценки координат ИРИ в пространстве

17. Вычислитель 4. Вычисление ковариационной матрицы оценок координат ИРИ на плоскости

18. Вычислитель 5. Вычисление ковариационной матрицы оценок координат ИРИ в пространстве

19. Эллипс рассеяния для оценки координат ИРИ

20. Эллипсоид рассеяния для оценки координат ИРИ

21. Блок вывода результатов

22. Выход

Определение азимутальных и угломестных пеленгов

Процедура определения координат ИРИ базируется на определении азимутальных и угломестных пеленгов, на основании которых определяются уравнения прямых линий на плоскости и в пространстве. Точка пересечения последних определяет координаты источника излечений. Рассмотрим предлагаемый способ определения пеленгов источника излучения. Как показано в прототипе, результаты, полученные в одной системе координат, легко пересчитываются в другие системы координат. Выберем декартову прямоугольную систему координат.

Предлагаемый способ определения пеленгов на АС любой конфигурации заключается в том, что АС любой конфигурации можно свести к линейной, к системе круговых АС с общим фазовым центром и т.п. От полученной функции, описывающей комплексную огибающую сигнала ИРИ на выходе элементов АС, и от комплексных чисел на элементах АС берется натуральный логарифм. Приравниваются соответствующие действительные и мнимые части. Из равенства действительных частей определяется амплитуда сигнала, а из равенства мнимых - фазы. Записывая равенства мнимых частей для всех элементов АС, получаем систему алгебраических уравнений, из которой определяем азимутальный и угломестный пеленги, а также начальную фазу сигнала. Для предлагаемого способа необходимо иметь не менее двух элементов АС, отстоящих на разные углы от направления отсчета.

Предлагаемый способ определения пеленгов источника излучения продемонстрируем на примере круговой (кольцевой) АС.

1. В круговой АС каждый элемент смещен на некоторый угол от другого, т.е. круговая АС автоматически разделена на число областей, равное числу вибраторов. Восстанавливается вектор комплексных амплитуд сигналов y=[y₁y_2…y_M]^Т, полученных с выхода каждого элемента АС.

2. Запишем нелинейную систему уравнений, правая часть которой является аналитическим выражением комплексной амплитуды сигнала на m-ом элементе АС, комплексной огибающей выходов элементов круговой АС

где m=1, …, n;

j - мнимая единица, j = − 1 ,

θ - азимутальный пеленг,

β - угломестный пеленг,

γ_m - угол между m-ым вибратором и направлением отсчета,

f₀ - частота сигналов, излучаемых пеленгуемыми ИРИ,

u - амплитуда сигнала,

φ₀ - начальная фаза сигнала,

t - время, в данном случае его можно положить равным нулю,

λ - длина волны сигналов ИРИ,

R - радиус антенной системы.

3. Запишем натуральный логарифм выражения (1), получим

Обозначим argy_m=P_m и приравняем соответственно действительные и мнимые части. Действительные части u=|y_m|; амплитуду u определили.

Приравниваем мнимые части:

или

где ; γ₁=0 - начало отсчета.

4. Составим систему уравнений для пеленгов θ, β и начальной фазы сигнала ϕ ⌢ 0 :

Решить эту систему (3) можно разными методами - матричным и нематричным, как кому привычнее.

Приведем следующий.

Переносим ϕ ⌢ 0 вправо, делим все уравнения на первое. Получим новую систему

или в матричном виде: A θ → = Y ,

где

Отсюда решение

Сразу получаем оценку начальной фазы сигнала φ₀, затем определяем оценку азимутального пеленга θ из найденного значения tg   θ(P 1 − ϕ ⌢ 0 ) и оценку угломестного пеленга β. Поскольку получены аналитические формулы для вычисления начальной фазы сигнала φ₀, азимутального пеленга θ, а затем угломестного пеленга β, то для них достаточно просто вычислить дисперсии, как для функции случайного аргумента [3].

Решить систему (3) можно и другим способом. Вычтем первое уравнение из остальных (исключим начальную фазу φ₀), получим новую систему

Разделим все полученные уравнения на одно из них и проведем преобразования. Найдем оценки азимутального пеленга θ и угломестного пеленга β. Продемонстрируем эту процедуру на первых двух уравнениях новой системы. Разделим первое уравнение на второе

Сократим на cos β

Обозначим

;

А и В известные константы, т.е. получаем

Из условия

при известном θ получим

Пеленги θ и β определяются по каждому элементу АС. Из полученного ряда значений определяется среднее значение пеленгов, их дисперсии и коэффициенты корреляции.

Следует отметить, что операции, имеющие место в формулах (2) и (3), (5) и (6), не представляют большой вычислительной сложности и, соответственно, требуют малых временных затрат и уменьшает ошибку в определении пеленгов, поскольку предлагаемый алгоритм учитывает или исключает начальную фазу сигнала φ₀, влияющую на значение пеленгов.

Предлагаемый способ может применяться в совокупности с любым способом пеленгации (при любой конфигурации АС) при регистрации одного сигнала на выделенной частоте для определения значений азимутальных и угломестных пеленгов ИРИ, т.к. вычисление произведения косинусов азимутального и угломестного пеленгов гораздо менее сложная операция, чем вычисление упомянутых пеленгов по отдельности. Тем более, что в предлагаемом методе не применяются одномерные, двух- и трехмерные сетки значений θ, β, φ₀.

Реализация алгоритма определения пеленгов:

1. Для функционирующей АС (до проведения измерений) аналитически вычисляется натуральный логарифм (2) от функции, описывающей комплексную огибающую выходов элементов АС (1).

2. Вычисляется натуральный логарифм измеренных комплексных амплитуд сигналов с каждого элемента АС.

3. Действительные и мнимые части полученного аналитического выражения натурального логарифма комплексной огибающей выходов элементов АС (2) приравниваются соответственно к действительным и мнимым частям натурального логарифма измеренных комплексных амплитуд сигналов с каждого элемента АС.

4. Получают систему алгебраических уравнений (3), из которой определяются аналитические выражения для вычисления азимутального пеленга θ, угломестного пеленга β, начальной фазы сигнала φ₀.

5. Согласно формулам (4) или (5), (6) вычисляются азимутальный пеленг θ, начальная фаза сигнала φ₀, а затем угломестный пеленг β.

6. Поскольку известны аналитические формулы для вычисления начальной фазы сигнала φ₀, азимутального пеленга θ, а затем угломестного пеленга β, то их дисперсии вычисляют, как для функции случайного аргумента [3].

При независимых переменных дисперсия функции f(x) вычисляется по следующей формуле

В нашем случае в качестве f(x) выступают формулы для cosβ, tgθ, φ₀. В качестве x_i выступают все другие переменные, входящие в формулу. Например: ; тогда f(x)=cosβ, P₁≡x_z; φ₀≡x₂; cosθ≡х₃.

Компьютеру задаются матрицы и формула (3), компьютер выдает два числа со своими среднеквадратическими отклонениями: значения t g θ ( P 1 − ϕ ⌢ 0 ) = α 1 и φ₀=α₂. Тогда и φ₀=α₂; .

Можно поступить по-другому, записать функционал метода наименьших квадратов для второй системы:

минимизировать

Тогда значение tgθ находится из условия ∂ F ∂ t g θ = 0 ; φ₀ - из условия .

В компьютере пеленги и начальные фазы сигналов и их погрешности рассчитываются по явным формулам и не требуют много времени.

Приведем результаты получаемых значений азимутального пеленга θ и угломестного пеленга β предлагаемым способом, используя три элемента АС (первые три уравнения). По предлагаемому способу пеленг θ равен

Рассмотрим числовой пример.

На круговой АС радиусом 50 м на частоте 1 мегагерц при соотношении сигнал/шум, равном 10, зарегистрирован сигнал. На первых трех вибраторах зарегистрированы следующие фазы: P₁=35 град., Р₂=Р₃=45,98 град. Угол между элементами АС γ_m равен 30 град. Подставим исходные данные в формулу

Для первого вибратора получим:

Аналогично, для второго - 45,98=60 cos(θ-30)cosβ+φ₀;

для третьего - 45,98=60 cos(θ-60)cosβ+φ₀.

По формулам (4) получено: θ=45 град., β=45 град., φ₀=5 град.

Среднее квадратическое отклонение (СКО) θ равно 0, 006 град., СКО β равно 0,009 град.

С увеличением значения φ₀ ошибка резко возрастает.

Модельный расчет пеленга проводился на компьютере с процессором с тактовой частотой 2 ГГц. Время счета порядка 0,001 сек. При ручном счете потребуется порядка 1 мин, т.к. в каждом измерении изменяются только P_m.

Определение координат источника излучения путем объединения всей информации по пеленгам

Нам известен набор пеленгов и их погрешностей от разных источников. Координаты регистраторов сигналов и погрешности этих координат также известны. Азимутальный и угломестный пеленги определяют координаты направляющего вектора прямой в пространстве, проходящей через точку с известными координатами (регистратор сигналов), и через точку с неизвестными координатами X и Y (источник излучения). Каноническое уравнение прямой в пространстве, проходящей через точку M₁(x₀, y₀, z₀) параллельно вектору S ¯ = l i ¯ + m j ¯ + n k ¯ , имеет вид: .

Уравнение этой же прямой может быть записано как пересечение двух плоскостей

Уравнение прямой на плоскости (например, на плоскости XY)

Введем l=cosα; m=sinα. Тогда

xsinα-ycosα=x₀sinα-γ₀cosα или, после деления на cosα,

xtgα-y=x₀tgα-y₀; или xtgα-y=b, где b=x₀tgα-y₀.

В данном уравнении прямой две случайные величины: tgα и b. При известных дисперсиях σ²(x₀); σ²(y₀); σ²(α) получим дисперсию

Собрав данные о пеленгах с разных источников, получим систему уравнений

xtgα_i-y=b_i; i=1, …, N,

в которой надо определить координаты (x, y) источника излучений. Метод наименьших квадратов применить нельзя, т.к. он применим только в случае, если в левой части уравнения нет случайных величин. Если мы запишем уравнение с правыми частями b_i и tgα_i, то получим две пересекающиеся прямые. В данном случае надо применить методы конфлюэнтного анализа - построить линию ортогональной регрессии, которая учитывает погрешности всех исходных данных. Получим следующий функционал

точка минимума которого определяет точечные оценки координат источника излучения. Для этого надо решить систему двух уравнений с двумя неизвестными X и Y:

Ковариационная матрица точечных оценок X и Y - матрица M

Уравнение прямой в пространстве эквивалентно системе уравнений плоскостей m(x-x₀)-1(y-y₀)+0z=0

0x+n(y-y₀)-m(z-z₀)=0

Система для определения координат (x, y, z) источника излучения в данном случае будет иметь 2N уравнений с тремя неизвестными (x, y, z) и содержит четыре случайные величины: σ²(b_1i), σ²(b_2i)

(m_i/l_i), (n_i/m_i), где b_li=(m_i/l_i)х₀-y₀, b_2i=(n_i/m_i)y_0i-z_0i

Очевидно, что эта система распадается на две системы уравнений: на плоскости XY и на плоскости YZ.

Функционал конфлюэнтного апализа в данном случае имеет следующий вид:

Оценки координат ИРИ иычисляются из системы уравнений

Ковариационная матрица точечных оценок x, y и z - матрица М

Оценки координат ИРИ и их погрешности рассчитываются по явным формулам и не требуют много времени.

Реализация алгоритма

1. Прежде всего