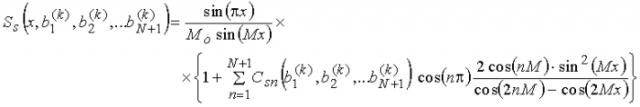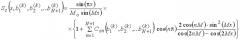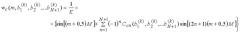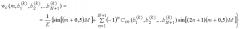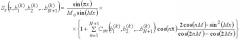Способ гармонического анализа периодического многочастотного сигнала на фоне шума

Способ гармонического анализа периодического многочастотного сигнала на фоне шума

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и предназначено для гармонического анализа периодических колебательных процессов, в частности электрических сигналов.

В измерительной технике известны различные способы гармонического (спектрального) анализа периодического многочастотного сигнала, заключающиеся в определении гармонического состава периодического многочастотного сигнала y ( t ) и оценивании частот, амплитуд и фаз входящих в сигнал гармоник.

Известен эффективный способ спектрального анализа сигнала [1] на основе дискретного преобразования Фурье в котором для снижения погрешности оценки частоты, вызванной дискретностью спектра, искусственно увеличена длительность периода повторения реализации сигнала путем добавления нулевых отсчетов к исходной реализации. Предельным случаем этого способа является использование дискретно-временного преобразования Фурье, эквивалентного обработке реализации сигнала с бесконечным периодом, и исключающего погрешности оценки частоты и амплитуды сигнала за счет дискретности спектра.

Однако в этом способе не исключено влияние боковых лепестков слагаемых спектра на точность определения частот, фаз и амплитуд составляющих анализируемого сигнала.

Для уменьшения погрешности, обусловленной влиянием боковых лепестков слагаемых спектра на положения спектральных пиков, широко используется способ гармонического анализа сигнала y ( t ) [2], включающий получение отсчетов y ( m ) сигнала через равные интервалы времени Δ t , перемножение отсчетов y ( m ) сигнала с отсчетами весовой функции w ( m ) , вычисление спектра путем нахождения Фурье-образа полученного произведения и оценку частот слагаемых сигнала.

Практическое осуществление этого способа выполняют методами цифровой обработки сигналов.

Известен способ гармонического анализа сигнала y ( t ) [3], включающий получение цифровых отсчетов y ц ( m ) сигнала через равные интервалы времени Δ t , перемножение цифровых отсчетов y ц ( m ) сигнала с отсчетами весовой функции w ( m ) ц , вычисление спектра путем нахождения Фурье-образа полученного произведения и оценку частот слагаемых сигнала [3, стр. 129, 273 - 274].

Известно, что обработка сигналов с помощью ВФ позволяет ослабить влияние боковых лепестков слагаемых спектра, но лишь за счет ухудшения спектрального разрешения. Считается, что в результате этих противоречий при использовании спектрального анализа на основе преобразования Фурье погрешность оценки частоты и амплитуды сигнала с относительно широким спектром не может быть низкой [4, стр. 102]. Причем минимумы погрешности оценки частоты совпадают с максимумами погрешности оценки амплитуды.

Таким образом, способы спектрального анализа сигнала имеют существенную погрешность определения частот, амплитуд и фаз спектральных слагаемых анализируемого сигнала из-за взаимного влияния боковых лепестков слагаемых спектра и низкой разрешающей способности.

Снижение взаимного влияния боковых лепестков слагаемых спектра предложено в итерационном способе гармонического анализа периодического многочастотного сигнала y ( t ) с периодом T [5], являющемся прототипом, цикл которого включает получение цифровых отсчетов y ц ( m ) сигнала через равные интервалы времени Δ t , генерирование весовой функции w ( m ) ц в форме цифровых отсчетов, перемножение цифровых отсчетов y ц ( m ) сигнала с цифровыми отсчетами весовой функции w ( m ) ц , вычисление спектра путем нахождения Фурье-образа полученного произведения, оценивание частот x i ,...., x j пиков спектра, превышающих уровень боковых лепестков наиболее интенсивного слагаемого спектра, и оценивание частот, амплитуд и фаз гармонических составляющих сигнала по частотам, амплитудам и фазам Фурье-образа, полученного произведения, на частотах x i ,...., x j пиков спектра. Затем многократно выполняют дополнительные циклы гармонического анализа. В каждом дополнительном цикле гармонического анализа по результатам выполненного ( k − 1 ) цикла гармонического анализа изменяют форму весовой функции генерированием новых цифровых отсчетов весовой функции, повторяя циклы гармонического анализа до получения на частоте каждого из анализируемых гармонических составляющих сигнала допустимых значений слагаемых спектра от заданного количества других гармонических составляющих сигнала и допустимых значений заданного количества производных слагаемых спектра от заданного количества других гармонических составляющих сигнала.

Цифровые отсчеты весовой функции w ( m ) ц генерируют по отсчетам дискретной весовой функции, определенной одним из двух выражений. Первое выражение имеет вид

w s ( m , b 1 , b 2 ... b N ) = 1 + ∑ n = 1 N ( − 1 ) n C s n ( b 1 , b 2 ,.., b N ) cos [ 2 n ( m + 0,5 )   M ] ,

где m - номер текущего отсчета сигнала;

b i = ω i T / 2 π - нормированная частота, на которой задается равенство нулю спектр весовой функции или его производная;

ω i − отсчеты угловой частоты;

T - период;

N - число тригонометрических слагаемых весовой функции, равное суммарному числу варьируемых нулей спектра ВФ и нулей его производных;

n - номер тригонометрического слагаемого;

C s n ( b 1 , b 2 ,.., b N ) = ( − 1 ) n + 1 cos ( n M ) ⋅ ∏ i = 1 N [ cos ( 2 n M ) − cos ( 2 b i M ) 2 sin 2 ( b i M ) ] ⋅ ∏ p = 1 p ≠ n N [ 1 − cos ( 2 p M ) ] cos ( 2 n M ) − cos ( 2 p M ) ;

M = π / M 0 ;

M 0 - число отсчетов сигнала.

Второе выражение имеет вид

w c ( m , b 1 , b 2 ... b N ) = 1 K { sin [ ( m + 0,5 )   M ] + ∑ n = 1 N ( − 1 ) n C c n ( b 1 , b 2 ,..., b N ) sin [ ( 2 n + 1 ) ( m + 0,5 )   M ] } ,

где

K = − 2 M o { sin ( 0,5 M ) cos   ( M ) − 1 + ∑ n = 1 N C c n ( b 1 , b 2 ,..., b N ) cos ( n π ) sin [ M ( n + 0,5 ) ] cos [ M ( 2 n + 1 ) ] − 1 } ;

C с n ( b 1 , b 2 ,.., b N ) = ( − 1 ) n + 1 sin ( 0,5 M ) sin [ ( n + 0,5 )   M ] ×

× ∏ i = 1 N { cos [ ( 2 n + 1 ) M ] − cos ( 2 b i M ) cos ( M ) − cos ( 2 b i M ) } ⋅ ∏ p = 1 p ≠ n N cos ( M ) − cos [ ( 2 p + 1 ) M ] cos [ ( 2 n + 1 ) M ] − cos [ ( 2 p + 1 ) M ] .

Изменение формы весовой функции задают изменением положений нулей b i спектра весовой функции

S s ( x , b 1 , b 2 ,... b N ) = sin ( π x ) M o sin ( M x ) × { 1 + ∑ n = 1 N C s n ( b 1 , b 2 ,... b N )     cos ( n π ) 2 cos ( n M ) ⋅ sin 2 ( M x ) cos ( 2 n M ) − cos ( 2 M x ) }   ,

или S c ( x , b 1 , b 2 ,... b N ) = − cos ( π x ) cos ( M x ) 0,5 M o K ⋅ { sin ( 0,5 M ) cos ( M ) − cos ( 2 M x ) +

+ ∑ n = 1 N C c n ( b 1 , b 2 ,... b N ) cos ( n π ) sin [ M ( n + 0,5 ) ] cos [ M ( 2 n + 1 ) ] − cos ( 2 M x ) } ,

где x = ω T / 2 π - текущая нормированная частота;

ω - текущая угловая частота.

При выполнении ( k ) цикла гармонического анализа по оцененным частотам

x i ( k − 1 ) ,...., x j ( k − 1 ) пиков спектра в ( k − 1 ) цикле гармонического анализа, которые превышают уровень боковых лепестков наиболее интенсивного слагаемого спектра, вычисляют взаимные разности между частотами x i ( k − 1 ) ,...., x j ( k − 1 ) пиков спектра Δ x i ( k − 1 ) = x i ( k − 1 ) − x j ( k − 1 ) и корректируют форму весовой функции путем задания частот нулей спектра и нулей его производных b i ( k ) равными модулям взаимных разностей между частотами пиков спектра b i ( k ) = | Δ x i ( k − 1 ) | . Затем используют весовую функцию со скорректированной формой в ( k ) цикле гармонического анализа, при этом за частоты гармонических составляющих принимают оценки на последнем цикле гармонического анализа.

Изменение формы весовой функции выполняют до снижения модуля разности между вновь полученными значениями оценок частот x i ( k ) ,...., x j ( k ) пиков спектра и их предыдущими значениями x i ( k − 1 ) ,...., x j ( k − 1 ) ниже контрольного уровня Δ x :

| x i ( k ) − x i ( k − 1 ) | ≤ Δ x ,…, | x j ( k ) − x j ( k − 1 ) | ≤ Δ x .

Амплитуду и фазу каждого составляющего сигнала оценивают после уточнения частот пиков спектра.

Для оценки частот гармонических составляющих многочастотного сигнала в первом цикле применяют весовую функцию такой формы, при которой для минимальной разности частот между гармоническими составляющих сигнала не происходит перекрытия основных лепестков слагаемых спектра сигнала, а уровень боковых лепестков спектра весовой функции не превышает заданного. При этом основной лепесток слагаемого спектра, соответствующий наиболее слабому из анализируемых составляющему сигнала, превышает уровень боковых лепестков слагаемого спектра наиболее интенсивного составляющего сигнала, которые определяют на основе априорных сведений о возможном гармоническом составе сигнала.

В последнем цитируемом способе максимально ослаблено влияние боковых лепестков от каждого из анализируемых гармонических слагаемых спектра на результаты измерений параметров гармонических слагаемых сигнала, но сохраняется существенное влияние шума на точность определения частот, фаз и амплитуд, составляющих анализируемого сигнала.

Технический результат, на достижение которого направлено изобретение способа, заключается в одновременном уменьшении погрешности измерения частот амплитуд и фаз гармонических составляющих периодического многочастотного сигнала на фоне шума.

Указанный технический результат достигается тем, что в способе гармонического анализа периодического многочастотного сигнала y ( t ) с периодом T , цикл которого включает получение цифровых отсчетов y ц ( m ) сигнала через равные интервалы времени Δ t , генерирование весовой функции w ( m ) ц в форме цифровых отсчетов, перемножение цифровых отсчетов y ц ( m ) сигнала с цифровыми отсчетами весовой функции w ( m ) ц , вычисление спектра путем нахождения Фурье-образа полученного произведения, оценивание частот x i ,..., x j пиков спектра, превышающих уровень боковых лепестков наиболее интенсивного слагаемого спектра и оценивание частот, амплитуд и фаз гармонических составляющих сигнала по частотам, амплитудам и фазам Фурье-образа полученного произведения на частотах x i ,..., x j пиков спектра, многократное выполнение дополнительных циклов гармонического анализа, в каждом из которых по результатам выполненного ( k − 1 ) цикла гармонического анализа изменяют форму весовой функции генерированием новых цифровых отсчетов весовой функции путем задания частот нулей спектра ВФ и нулей его производных b i ( k ) равными модулям взаимных разностей между частотами пиков спектра b i ( k ) = | x i ( k − 1 ) − x j ( k − 1 ) | , использование весовой функции со скорректированной формой в ( k ) цикле гармонического анализа, повторение циклов гармонического анализа до получения на частоте каждого из анализируемых гармонических составляющих сигнала допустимых значений слагаемых спектра от заданного количества других гармонических составляющих сигнала и допустимых значений заданного количества производных слагаемых спектра от заданного количества других гармонических составляющих сигнала и принятие за частоты гармонических составляющих оценки на последнем цикле гармонического анализа, с соблюдением следующих условий дополнительно выполняют следующую совокупность действий. Выполняют, по меньшей мере, один дополнительный цикл гармонического анализа, в котором по результатам выполненного гармонического анализа изменяют форму весовой функции генерированием новых цифровых отсчетов весовой функции путем одновременного задания частот нулей спектра ВФ и нулей его производных b i ( k ) равными модулям взаимных разностей между частотами пиков спектра b i ( k ) = | x i ( k − 1 ) − x j ( k − 1 ) | и одного дополнительного нуля спектра ВФ.

Возможно генерирование отсчетов весовой функции с одновременным заданием суммарного числа N частот нулей спектра ВФ и нулей его производных b i ( k ) равными модулям взаимных разностей между частотами пиков спектра b i ( k ) = | x i ( k − 1 ) − x j ( k − 1 ) | и одного дополнительного N + 1 нуля спектра ВФ после снижения абсолютного значения разности между вновь полученными значениями оценок частот пиков спектра x i ( k ) ,...., x j ( k ) и их предыдущими значениями x i ( k − 1 ) ,...., x j ( k − 1 ) ниже контрольного уровня Δ x

| x i ( k ) − x i ( k − 1 ) | ≤ Δ x ,…, | x j ( k ) − x j ( k − 1 ) | ≤ Δ x .

Предпочтительно в каждом цикле гармонического анализа начиная со второго изменение формы весовой функции генерированием новых цифровых отсчетов весовой функции путем одновременного задания суммарного числа N частот нулей спектра ВФ и нулей его производных b i ( k ) равными модулям взаимных разностей между частотами пиков спектра b i ( k ) = | x i ( k − 1 ) − x j ( k − 1 ) | и одного дополнительного N + 1 нуля спектра ВФ.

При выполнении ( k ) цикла гармонического анализа по оцененным частотам x i ( k − 1 ) ,...., x j ( k − 1 ) пиков спектра в ( k − 1 ) цикле гармонического анализа вычисляют взаимные разности между частотами пиков спектра Δ x i ( k − 1 ) = x i ( k − 1 ) − x j ( k − 1 ) и корректируют форму весовой функции путем одновременного задания суммарного числа N частот нулей спектра и нулей его производных b i ( k ) равными модулям взаимных разностей между частотами пиков спектра b i ( k ) = | Δ x i ( k − 1 ) | и дополнительного N + 1 нуля b N + 1 ( k )

b N + 1 ( k ) = [ ∑ n = 1 N + 1 A s n 2 n 4 ( ( b 1 ( k ) ) 2 − n 2 ) 2 ... ( ( b N ( k ) ) 2 − n 2 ) 2 ∑ n = 1 N + 1 A s n 2 n 2 ( ( b 1 ( k ) ) 2 − n 2 ) 2 ... ( ( b N ( k ) ) 2 − n 2 ) 2 ] 1 2

в спектре

S s ( x , b 1 ( k ) , b 2 ( k ) ,... b N + 1 ( k ) ) = sin ( π x ) M o sin ( M x ) ×                     × { 1 + ∑ n = 1 N + 1 C s n ( b 1 ( k ) , b 2 ( k ) ,... b N + 1 ( k ) )     cos ( n π ) 2 cos ( n M ) ⋅ sin 2 ( M x ) cos ( 2 n M ) − cos ( 2 M x ) }

весовой функции

w s ( m , b 1 ( k ) , b 2 ( k ) ,... b N + 1 ( k ) ) = 1 + ∑ n = 1 N + 1 ( − 1 ) n C s n ( b 1 ( k ) , b 2 ( k ) ,... b N + 1 ( k ) ) cos [ 2 n ( m + 0,5 )   M ] ,

где A s