Способ определения нестационарного теплового потока

Способ определения нестационарного теплового потока

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к области тепловых измерений и может быть использовано при исследовании теплообмена и управления процессами в металлургии, энергетике и других отраслях народного хозяйства.

Из существующего уровня известен способ измерения тепловых потоков, сущность которого заключается в измерении двумя гипертермопарами, расположенными одна за другой, двух перепадов температур на чувствительном элементе, вычислении скорости изменения перепада температур, измеренного второй гипертермопарой, и определении нестационарного теплового потока по формуле (см. а.с. СССР N 1045011, G01K 17/08, 1982 г.).

Недостатком способа является низкая точность измерения нестационарного теплового потока.

Из известных способов наиболее близким по технической сущности является способ измерения нестационарного теплового потока (см. а.с. СССР N 1024751, G01K 17/08, 1981 г.), заключающийся в измерении перепада температур на чувствительном элементе, скорости изменения температуры на приемной и обратной поверхности чувствительного элемента и определении величины нестационарного потока по формуле

q = λ b ( t 0 − t b ) + c ρ b 6 ( 2 t 0 ' + t b ' ) ,

где λ, с, ρ, b - теплопроводность, теплоемкость, удельная плотность и толщина чувствительного элемента;

t₀, t_b - температуры приемной и обратной поверхностей чувствительного элемента;

t 0 ' и t b ' - скорости изменения температур приемной и обратной поверхностей чувствительного элемента.

Недостатком способа является низкая точность измерения нестационарного теплового потока вследствие большой динамической погрешности и погрешности из-за влияния конвективного теплообмена боковой поверхности тепломера.

В основу изобретения положена задача разработать способ, обеспечивающий повышение точности определения нестационарного теплового потока.

Для решения поставленной задачи в известном способе измерения нестационарного теплового потока, включающем измерение разности и скорости изменения средних температур приемной и обратной поверхностей тепломера, дополнительно измеряют в сечениях тепломера скорость изменения средней по площади температуры и температуру в точках его боковой поверхности, а тепловой поток определяют по формуле

q ( τ ) = λ H [ t ¯ 0 ( S ) ( τ ) − t ¯ H ( S ) ( τ ) ] + C H ∑ k = 0 m p k ∂ t ¯ k ( S ) ( τ ) ∂ τ + q ¯ α ( H ) ( τ ) ,

где λ, С - теплопроводность и объемная теплоемкость материала тепломера;

H, S, τ - толщина, площадь поперечного сечения тепломера и время;

p_k - весовой коэффициент при средней скорости изменения температуры;

m+1 - количество сечений тепломера, в которых измеряется скорость изменения средней температуры;

q ¯ α ( H ) ( τ ) - поправка на конвективный теплообмен боковой поверхности тепломера, определяемая по измеренной температуре в точках на боковой поверхности, его геометрическим размерам и коэффициенту теплообмена;

t ¯ 0 ( S ) ( τ ) , t ¯ H ( S ) ( τ ) , t ¯ k ( S ) ( τ ) - средняя по площади тепломера температура соответственно, на его приемной, обратной поверхностях и в сечениях, перпендикулярных распространению измеряемого теплового потока.

Дополнительное измерение в сечениях тепломера скорости изменения средней по площади температуры и температуры в точках его боковой поверхности позволяет уменьшить динамическую погрешность измерения теплового потока и учесть влияние конвективного теплообмена боковой поверхности тепломера.

Для обоснования повышения точности необходимо рассмотреть основные положения теории, на которой базируется заявленный способ. Он основан на математическом описании теплопередачи в объекте исследования в виде интегральной формы уравнения теплопроводности. Для тепломера, имеющего форму цилиндра с радиусом основания R и толщиной H, который одним основанием воспринимает измеряемый нестационарный тепловой поток, а на боковой поверхности действует конвективный тепловой поток, интегральная форма уравнения теплопроводности имеет вид

q ( τ ) = q ¯ λ ( H ) ( τ ) + q ¯ C ( H ) ( τ ) + q ¯ α ( H ) ( τ ) ,

где q ¯ λ ( H ) ( τ ) = λ H [ t ¯ ( S ) ( 0, τ ) − t ¯ ( S ) ( H , τ ) ] ; q ¯ C ( L ) ( τ ) = C H ∂ ∂ τ ∫ 0 H d x ∫ 0 x t ¯ ( S ) ( x , τ ) d x ; q ¯ α ( H ) ( τ ) = 2 α R H ∫ 0 H d x ∫ 0 x t ( x , R , τ ) d x ; t ¯ ( S ) ( x , τ ) - распределение по толщине тепломера средней на площади его поперечного сечения температуры; λ, С, α, τ - теплопроводность, объемная теплоемкость материала тепломера, коэффициент теплопередачи и время.

Для тепломера в виде параллелепипеда интегральная форма отличается видом выражения для определения среднего по толщине конвективного теплового потока q ¯ α ( H ) ( τ ) . Данная модель является точным математическим описание теплопередачи в тепломере, не привязанным к решениям уравнения теплопроводности и условиям его выполнения. Она представляет собой баланс средних по толщине тепломера тепловых потоков, действующих на граничных поверхностях q(τ), q ¯ α ( H ) ( τ ) проходящего через тепломер q ¯ λ ( H ) ( τ ) вследствие теплопроводности материала и аккумулированного q ¯ C ( H ) ( τ ) в нем из-за его теплоемкости. Справедливость данной формы представления уравнения теплопроводности была проверена на различных аналитических и дискретных моделях, а также экспериментально. Для одномерного варианта данная интегральная форма может быть получена путем двукратного интегрирования дифференциального уравнения теплопроводности с пределами от 0 до x и от 0 до H. Повторные интегралы вида ∫ 0 H d x ∫ 0 x t ¯ ( S ) ( x , τ ) d x , ∫ 0 H d x ∫ 0 x t ( x , R , τ ) d x определяются аналогично однократному интегралу ∫ 0 H t ¯ ( S ) ( x , τ ) d x , ∫ 0 H t ( x , τ ) d x , по приближенной формуле

∫ 0 H d x ∫ 0 x t ( x , τ ) d x = ∑ k = 0 m p k t ( x k , τ ) , ∫ 0 H d x ∫ 0 x t ¯ ( S ) ( x , τ ) d x = ∑ k = 0 m p k t ¯ ( S ) ( x k , τ ) ,

где p k = ∫ 0 H ∫ 0 x ∏ i = 0 m ( x − x i ) / ∏ i = 0 m ( x k − x i ) d x d x ; ( k = 0, m ¯ ) , (i≠k) - весовой коэффициент; t(x_k, τ) - температура в точке x_k; m+1 - количество точек на интервале [0, H], данная формула основана на многочлене Лагранжа; она является точной для многочлена степени m.

В простейшем случае, когда распределение температуры по толщине тепломера одномерно, т.е. отсутствует теплообмен с боковой поверхности, и близкое к линейному, то формула для определения повторного интеграла принимает вид

∫ 0 H d x ∫ 0 x t ( x , τ ) d x = H 2 6 [ 2 t ( 0, τ ) + t ( H , τ ) ] .

Тогда из интегральной формы уравнения теплопроводности можно получить расчетную формулу прототипа:

q ( τ ) = λ H [ ( t ( 0, τ ) − t ( H , τ ) ] + c ρ H 6 ( 2 t ' ( 0, τ ) + t ' ( H , τ ) ] .

Чем больше количество точек на заданной толщине тепломера, тем выше степень полинома, который описывает распределение температуры, что соответствует уменьшению погрешность определения повторного интеграла и, следовательно, увеличению точности определения нестационарного теплового потока Графики, представленные на фиг.1 и фиг.2, иллюстрируют эффект дополнительного измерения температуры и скорости ее изменения в точках тепломера.

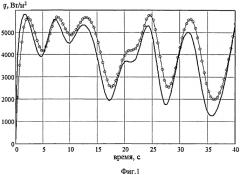
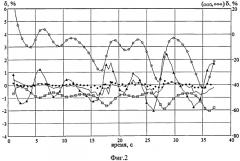
На фиг.1 показан пример изменения во времени плотности теплового потока, действующего на поверхности тепломера (сплошная тонкая линия), значения, рассчитанные по формуле заявляемого способа (символы) и по прототипу (полужирная линия). На фиг.2 приведены погрешности определения теплового потока для данного изменения теплового потока, рассчитанные по формуле заявленного способа: по шести точкам (); по четырем точкам с координатами - х=0r=0,75R, х=0,333H, r=0,75R, х=0,666H, r=0,75R, х=H, r=0,75R (); по двум точкам с координатами - x₀=0, r=0,75R; х=0,5H r=0,75R (); и рассчитанные по формулам аналога () и прототипа () (R=2,5 мм, H=1,2 мм). Погрешность по аналогу и прототипу находится в пределах от -40% до -60% и от -40% до 20%. Погрешность по заявленному способу, в зависимости от числа используемых точек, изменяется от ±0,5%, до ±2%. Повышение точности определения теплового потока достигнута за счет уменьшения динамической погрешности и учета влияния конвективного теплообмена боковой поверхности. Сущность изобретения поясняется чертежами, на которых изображено:

На фиг.1 - график изменения во времени плотности теплового потока, действующего на поверхности тепломера (сплошная тонкая линия), и значения, рассчитанные по формуле заявляемого способа (символы), и по прототипу (полужирная линия).

На фиг.2 - погрешности определения теплового потока, рассчитанные по формуле заявленного способа с различным количеством точек, по формулам аналога () и прототипа ().

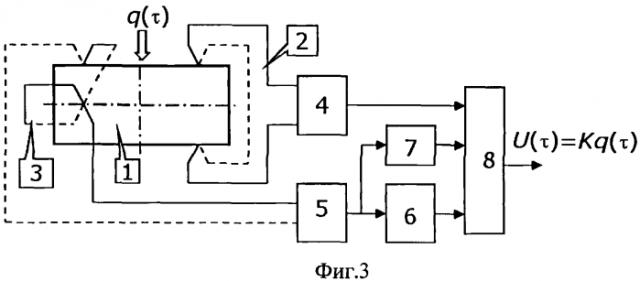
На фиг.3 - пример реализации заявленного способа.

Устройство, реализующее заявленный способ, состоит из тепломера 1 в виде цилиндра с радиусом основания R и устройства для обработки аналоговых сигналов. В нем использована приближенная формула определения повторного интеграла по двум точкам, одна из которых находится в среднем сечении, и которая является точной для параболического распределения температуры по толщине тепломера. В тепломере установлены: дифференциальная термопара 2 и термобатарея 3, рабочие спаи которых имеют координаты: х=0 r=0,75R, х=0,5Н r=0,75R, х=Н r=0,75R, измеряющие средние температуры по площади основания цилиндра в соответствующих сечениях тепломера по координате х. Устройство содержит: усилители термо-э.д.с. 4 и 5 для сигналов, пропорциональных соответственно разности температур и взвешенной суммы температур, дифференциатор 6, масштабирующий делитель напряжения 7 для получения сигнала, пропорционального величине поправки на теплообмен боковой поверхности q ¯ α ( H ) ( τ ) , и сумматор 8, выходное напряжение которого связано линейной зависимостью U(τ)=Kq(τ) с измеряемым тепловым потоком, где K - масштабирующий коэффициент. В устройстве реализована расчетная формула заявленного способа с учетом выбранной приближенной формулы определения повторного интеграла и определения поправки на теплообмен боковой поверхности по сигналу термобатареи.

Данный способ прошел экспериментальные исследования на лабораторной установке и теоретические исследования на различных одно- и двухмерных моделях тепломеров методом имитационного моделирования При вычислении погрешности определения теплового потока были использованы результаты имитационного моделирования его измерения на двухмерной модели с дискретностью по координатам h=0,1 мм цилиндрического тепломера диаметром D=5 мм и толщиной H=1,2 мм, имеющего теплопроводность λ=0,3 Вт/(м·К) и температуропроводность а=1,5 м²/с. На боковой поверхности и противоположной принимающей были приняты граничные условия 3 рода с коэффициентом теплообмена соответственно α=50 Вт/(м²·К) и α=100 Вт/(м²·K).

Способ определения нестационарного теплового потока, заключающийся в измерении разности и скорости изменения средних температур приемной и обратной поверхностей тепломера, отличающийся тем, что дополнительно измеряют в сечениях тепломера скорость изменения средней по площади температуры и температуру в точках его боковой поверхности, а тепловой поток определяют по формуле q ( τ ) = λ H [ t ¯ 0 ( S ) ( τ ) − t ¯ H ( S ) ( τ ) ] + C H ∑ k = 0 m p k ∂ t ¯ k ( S ) ( τ ) ∂ τ + q ¯ α ( H ) ( τ ) ,где λ, С - теплопроводность и объемная теплоемкость материала тепломера;Н, S, τ - толщина, площадь поперечного сечения тепломера и время;p_k - весовой коэффициент при средней скорости изменения температуры;m+1 - количество сечений тепломера, в которых измеряется скорость изменения средней температуры: q ¯ α ( H ) ( τ ) - поправка на конвективный теплообмен боковой поверхности тепломера; t ¯ 0 ( S ) ( τ ) , t ¯ H ( S ) ( τ ) , t ¯ k ( S ) ( τ ) - средняя по площади тепломера температура соответственно на его приемной, обратной поверхностях и в сечениях, перпендикулярных распространению измеряемого теплового потока.