Способ конструирования соприкасающихся тел с однонаправленным вращением и компьютерная система для реализации этого способа

Способ конструирования соприкасающихся тел с однонаправленным вращением и компьютерная система для реализации этого способа

Иллюстрации

Показать все

Реферат

Изобретение касается способа конструирования тел (изделий), которые при равнонаправленном вращении с одинаковой скоростью вокруг параллельно расположенных осей все время соприкасаются друг с другом по меньшей мере в одной точке.

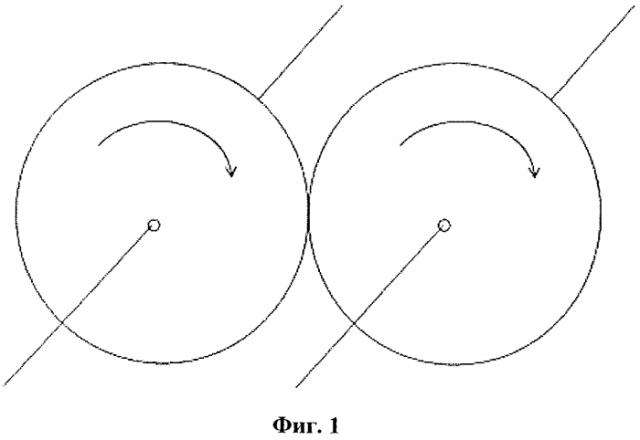
Рассмотрим два круга, которые расположены на параллельных осях рядом друг с другом, как это схематически изображено на фигуре 1. Общеизвестно, что круги при вращении в одинаковых направлениях касаются друг друга таким образом, что при вращении всегда имеется соприкосновение в одной точке, которая расположена между центрами вращения кругов.

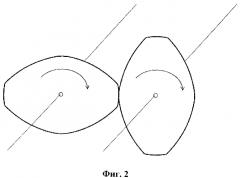
Кроме того, известно, что помимо кругов имеются и другие геометрические фигуры, которые при вращении в одном направлении всегда касаются друг друга в одной точке. Пример показан на фигуре 2. Эти фигуры при вращении в одном направлении с одинаковой скоростью всегда касаются друг друга в одной точке.

Двухмерные геометрические фигуры, представленные на фигурах 1 и 2, можно различным образом продолжать в третье измерение. Одна простая возможность - это, например, линейное продолжение фигур в направлении осей вращения, так чтобы образовывались дисковидные или стержневидные тела, которые при вращении в одной направлении касаются друг друга по линии между центрами вращения, которая проходит параллельно осям вращения.

Еще одна возможность состоит, например, в том, чтобы продлевать геометрические фигуры вдоль осей вращения винтообразно, так чтобы образовывались винтообразные тела. которые при вращении в одном направлении соприкасаются вдоль кривой между телами.

Тела, которые при равнонаправленном вращении вокруг параллельно расположенных осей с одинаковой скоростью всегда соприкасаются друг с другом по меньшей мере в одной точке, имеют значение, например, в технологии экструдеров, где их применяют в качестве шнековых экструдеров, вращающихся в одинаковых направлениях, например, для обработки вязких масс или в целях смешивания. Такие равнонаправленные двухвальные и многовальные экструдеры известны специалисту из патентной и специальной литературы. В качестве примера следует упомянуть следующую публикацию [1]: K.Kohlgrüber: "Der gleichläufige Doppelschneckenextruder", Hanser Verlag, 2007. To свойство, что соседние шнеки при равнонаправленном вращении попарно касаются друг друга, дает в случае шнековых экструдеров то преимущество, что они скоблят друг друга и поэтому друг друга очищают.

Для некоторых тел, которые при равнонаправленном вращении вокруг параллельно расположенных осей с одинаковой скоростью всегда соприкасаются друг с другом по меньшей мере в одной точке, существуют правила конструирования.

Так, например, из литературы по шнековым экструдерам известно (см., например, [1], стр.96-98), что шнековый элемент типа по Эрдменгеру с профилем сечения, как на фиг.2 настоящей заявки, можно составить из дуг окружности.

Неизвестно, однако, какие критерии должны быть выполнены в общем случае, чтобы два тела, вращающихся в одном направлении вокруг параллельно расположенных осей, все время касались друг друга по меньшей мере в одной точке.

Известно (см., например, [2]: Вооу «Geometry of fully wiped twin-screw equipment», Polymer Engineering and Science 18 (1978) 12, Seiten 973-984), что равнонаправленное вращение двух соприкасающихся тел вокруг фиксированных их осей идентично с точки зрения кинематики «сдвигу без вращения» одного тела вокруг другого, в этом случае фиксированного, тела. Эту особенность можно использовать для того, чтобы поэтапно создавать геометрические фигуры, которые при равнонаправленном вращении постоянно соприкасаются друг с другом в одной точке. При таком рассмотрении первая фигура («создаваемая») зафиксирована неподвижно, а вторую фигуру («создающую») поступательно перемещают вокруг первой по дуге окружности. Можно задать только часть профиля на второй фигуре и изучить, какой профиль при этом будет таким образом создан на первой фигуре. Создающая фигура в определенном смысле «вырезает» создаваемую.

Не известен, однако, общепринятый способ, позволяющий создать саму предварительно заданную часть второй фигуры. В [2] описан возможный подход, позволяющий генерировать участок профиля, из которого можно исходить, и из которого создают остальную часть профиля. Этот подход, однако, очень сложен с математической точки зрения и в первую очередь не универсален, то есть, можно создавать только такие профили, которые можно описать с помощью приведенных в [2] математических функций.

Поэтому, исходя из нынешнего уровня техники, поставлена задача представить общий способ, посредством которого можно конструировать тела, которые при равнонаправленном вращении с одинаковой скоростью вокруг двух параллельно расположенных осей всегда соприкасаются друг с другом по меньшей мере в одной точке.

Неожиданно были обнаружены основные принципы, составляющие базу для двух тел, которые при равнонаправленном вращении вокруг двух параллельно расположенных осей всегда соприкасаются друг с другом по меньшей мере в одной точке.

Исходя из этих основных принципов, можно вывести общий способ для конструирования таких тел.

Поэтому предметом настоящего изобретения является способ согласно независимому пункту 1 формулы изобретения для конструирования тел (изделий), которые при равнонаправленном вращении с одинаковой скоростью вокруг параллельно расположенных осей все время соприкасаются друг с другом по меньшей мере в одной точке. Предпочтительные формы исполнения находятся в зависимых пунктах формулы изобретения.

Способ согласно изобретению можно применять к двум или более телам. Тела расположены друг рядом с другом на параллельных осях вращения, попарно проходящих на расстоянии а друг от друга. Целесообразно описывать способ для двух тел K1 и K2, которые вращаются с одинаковой скоростью, каждое вокруг своей оси. При размещении более чем двух тел тела K1 и K2 всегда попеременно располагаются на соседствующих осях вращения.

Тела K1 и K2 в целях простоты изложения в настоящем тексте называют также соответствующими (соотносящимися) телами.

Скорость вращения - это число оборотов тела вокруг своей оси в единицу времени (единица измерения - герц).

Для конструирования соответствующих тел K1 и K2 сначала создают профили сечения этих тел. Профили сечения - это профили, которые получаются при сечении тел K1 и K2 плоскостью Е, которая проходит перпендикулярно осям вращения A1 и A2.

Неожиданно было обнаружено, что можно задать профиль сечения одного тела, а профиль сечения другого, соответствующего тела легко вывести из этого заданного профиля. При этом задаваемый профиль должен удовлетворять лишь немногим, простым в реализации критериям. Профиль соответствующего тела выводят простым образом либо начертательно (графически), либо путем расчетов. Это позволяет конструировать исключительно разнообразные соответствующие тела. Кроме того, это впервые дает возможность задавать практически любое тело и простьм образом выводить из заданного тела соответствующее ему тело. Способ согласно изобретению не ограничен профилями сечения, которые описывают дугами окружности (как в случае шнековых элементов типа по Эрдменгеру, см. [1] стр.96-98). Способ согласно изобретению также не ограничен описанными в [2] математическими функциями для определения профилей сечения.

Чтобы назвать критерии, которым должен удовлетворять задаваемый профиль сечения, задаваемый профиль целесообразно описать как математическую кривую.

Кривая (математическая) - это одномерный объект, у которого имеется кривизна. При этом «одномерный» означает, что по кривой можно перемещаться только в одном направлении (либо же в противоположном направлении). В данном случае кривая лежит в двухмерной плоскости Е, которая проходит перпендикулярно к осям вращения A1 и A2.

Точки пересечения S1 и S2 осей вращения A1 и A2 с плоскостью Е также называют центрами вращения конкретных осей. Расстояние между центрами вращения S1 и S2 составляет а.

Под кривизной кривой подразумевают изменение направления на единицу длины. Кривизна прямой везде равна нулю, поскольку ее направление не изменяется. У окружности радиуса r кривизна везде одинакова (а именно равна 1/r), поскольку ее направление везде изменяется в одинаковой мере. У всех остальных кривых кривизна обычно изменяется от точки к точке.

Кривизна некоторой кривой в некоторой точке P таким образом указывает, в какой мере кривая отклоняется от прямой в непосредственном окружении точки P.

Величину, обратную кривизне, называют радиусом кривизны. Это радиус окружности (круг кривизны), который в окрестности точки соприкосновения представляет собой наилучшее приближение (см. учебную литературу по математике, в частности, по геометрии).

Как известно специалисту, в параметрическом представлении кривую можно определить в зависимости от параметра s:

p → ( s ) = ( x ( s ) y ( s ) )

При этом x(s) и y(s) - это координаты точек кривой p → ( s ) в двухмерной плоскости E.

Чтобы из кривой, которая описывает профиль сечения тела K1, можно было создать профиль сечения соответствующего тела K2, эта кривая должна удовлетворять следующим критериям:

- Кривая должна быть замкнутой.

- Кривая должна быть непрерывной.

- Кривая должна быть выпуклой.

- Кривая на отдельных участках должна быть непрерывно дифференцируема.

- В каждой точке кривая p → должна иметь радиус кривизны ρ, который меньше расстояния а или равен ему.

Как известно, у замкнутой выпуклой кривой имеется следующее свойство.

Рассмотрим две произвольные точки P1 и P2 на кривой. Если эти точки P1 и P2 соединить прямой, то эта прямая пройдет через точки P1 и P2 кривой, но сверх того ни через одну другую точку на кривой, вне зависимости от того, где на кривой лежат точки P1 и P2.

Равным же образом для выпуклой кривой справедливо, что в каждой точке у кривой положительная кривизна. У кривой может быть один или несколько перегибов. В том случае, если имеются один или несколько перегибов, на участках между перегибами кривая непрерывно дифференцируема (что означает, непрерывно дифференцируема на отдельных участках). В том случае, когда перегибы отсутствуют, кривая целиком непрерывно дифференцируема. Возможность описать перегибы математически приведена ниже.

Если немногочисленные и простые в реализации вышеприведенные критерии выполнены, то из кривой p → можно вывести кривую q → , которая описывает профиль сечения соответствующего тела K2.

Для этого следует ввести еще несколько векторов (см., например, "HÜTTE, das Ingenieurwissen", 32-е издание, ISBN 3-540-20325-7, 2004, начиная со стр.59 [3]). Использованный способ записи соответствует стандартному математическому способу записи: вектор обозначают стрелкой над буквой, при этом точка над выражением в каждом случае представляет собой производную по параметру, черты модуля означают модуль вектора, то есть корень из скалярного произведения на самого себя, | x → | = x → ⋅ x → , а крест означает смешанное произведение.

Кроме того, из соображений простоты изложения сначала предполагают, что кривая полностью непрерывно дифференцируема, то есть, не имеет перегибов. В этом случае изложенные ниже соотношения справедливы для всех точек профиля сечения без ограничений. В случае же профилей сечения с одним или несколькими перегибами нижеизложенные соотношения справедливы для непрерывно дифференцируемых участков между перегибами.

- Пусть t → ( p → ) = p → ˙ | p → ˙ | - множество нормированных касательных векторов длины 1 (единичных касательных векторов).

Для каждой точки кривой p → существует нормированный касательный вектор, который в указанной точке проходит касательно к кривой p → .

- Пусть n → ( p → ) = t → ˙ | t → ˙ | это множество нормированных нормальных векторов длины 1, которые в каждом случае указывают в направлении центральной точки круга кривизны, принадлежащего к данной конкретной точке кривой p → .

Для каждой точки кривой p → существует нормированный нормальный вектор, который в указанной точке перпендикулярен касательной к кривой p → . Этот нормальный вектор направлен к центру того круга (круга кривизны), который аппроксимирует кривизну для данной конкретной точки кривой p → . Круг кривизны, принадлежащий к некоторой точке кривой, имеет тот же радиус (ту же кривизну), что и кривая в этой точке.

Тогда ρ = s ˙ 3 | p → ˙ × p → ¨ | - это радиус кривизны, причем s ˙ = | p → ˙ | .

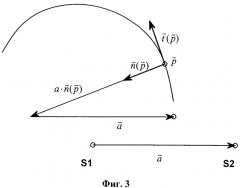
- Пусть a → - вектор длины a, который направлен от точки сечения S1 к точке сечения S2.

Кривую q → , которая описывает профиль сечения соответствующего тела K2 получают из кривой p → , описывающей предварительно заданный профиль сечения тела K1, посредством нижеследующего соотношения:

q → = p → + a ⋅ n → ( p → ) + a →                       ( 1 )

На фиг.3 схематически показана реализация способа согласно изобретению на основании одной точки на кривой. Точки пересечения S1 и S2 с осями вращения обозначены маленькими кружками. Они находятся на расстоянии а друг от друга. Вектор a → имеет длину a и направлен от S1 к S2. Над точками пересечения S1 и S2 показан участок кривой p → . Точка на кривой выделена и обозначена маленьким кружком. Из этой точки кривой p → можно создать точку на соответствующей кривой q → . Для получения точки на соответствующей кривой q → в точке кривой p → проводят касательную t → ( p → ) к кривой, строят нормированный нормальный вектор к этой касательной n → ( p → ) и удлиняют его в a раз, а затем, наконец, прибавляют к этому вектору a ⋅ n → ( p → ) вектор a → .

Кривую p → можно непрерывно описать одной математической функцией. Равным же образом кривую p → можно на отдельных участках описать разными математическими функциями.

Кривая p → на отдельных участках должна быть непрерывно дифференцируема. Таким образом, отдельные участки кривой p → , заданной на отдельных участках, не обязательно должны переходить друг в друга на границах с возможностью непрерывного дифференцирвания.

Если два участка кривой встречаются друг с другом в точке перегиба, то для точки перегиба не определен вектор касательной и нормальный вектор. Таким образом из отношения (1) для точки перегиба профиля тела K1 нельзя непосредственно вывести соответствующий участок кривой q → соответствующего тела K2.

Неожиданно было, однако, обнаружено, что каждому перегибу в профиле сечения тела K1 соответствует дуга окружности в профиле сечения тела K2.

Размер дуги окружности задается ее центральным углом и радиусом. В дальнейшем центральный угол дуги окружности для краткости называется углом дуги окружности. Положение дуги окружности задается положением его центра и положением обеих его конечных точек.

Дуга окружности в профиле сечения K2, соответствующая перегибу в профиле сечения тела K1, всегда имеет радиус, размер которого соответствует межосевому расстоянию a. Кроме того, дуга окружности, соответствующая перегибу, всегда характеризуется углом, который соответствует тому углу, под которым встречаются друг с другом касательные к участкам кривых в точке перегиба.

И наоборот, соответственно, справедливо утверждение, что сооветствующий участок профиля кривой q → представляет собой «перегиб», если участок профиля кривой p → - это дуга окружности с радиусом a.

В связи с этим целесообразно описывать перегиб дугой окружности, радиус которой равен 0. На перегибе происходит переход первого участка кривой во второй участок кривой посредством поворота на угол дуги окружности с радиусом, равным нулю. Касательная к первому участку кривой в центре дуги окружности с радиусом, равным нулю, пересекается с касательной ко второй дуге окружности также в центре дуги окружности под углом, соответствующим углу дуги окружности. Если учесть дугу окружности, то все соседствующие участки кривой (первый участок кривой → дуга окружности с радиусом, равным нулю, → второй участок кривой) переходят друг в друга по касательной. Целесообразно рассматривать дугу окружности с радиусом, равным нулю, как дугу окружности, радиус которой равен eps, причем eps - это очень малое положительное действительное число, стремящееся к 0 (eps<<1, eps→0). Из соответствующего профиля сечения формируется дуга окружности с тем же углом и радиусом, равным межосевому расстоянию.

Описанная ситуация проиллюстрирована на фигуре 7. На фигуре 7 показаны часть профиля сечения тела K1 и часть профиля сечения получающегося тела K2. Показанная часть профиля сечения тела K1 состоит из участков кривых KA1 и KA2. Эти участки кривых встречаются друг с другом в точке перегиба KP, которая обозначена маленьким кружком, то есть, профиль сечения тела K1 имеет перегиб. Как пояснено выше, перегиб предпочтительно описывать дугой окружности, радиус которой имеет нулевую величину. Угол дуги окружности равен углу W, который образуют друг с другом касательная TA1 к участку кривой KA1 и касательная TA2 к участку кривой KA2 в точке перегиба KP.

В пирофиле сечения тела K2, соответствующего телу K1, принадлежащие к участкам кривых KA1 и KA2 участки KA1' и KA2' получаются из отношения (1): q → = p → + a ⋅ n → ( p → ) + a → . При этом для кривой p → в уравнение (1) необходимо в каждом случае подставить участки кривых KA1 и KA2, так, чтобы в качестве кривой q → в итоге получились участки кривых KA1' и KA2'. Между получающимися участками кривых KA1' и KA2', которые обозначены на фигуре 7 штриховыми линиями, возникает пустое место.

Из перегиба в профиле сечения тела K1 в профиле сечения соответствующего тела K2 получается дуга радиусом r=a (a = межосевое расстояние между центрами вращения S1 и S2) и углом W. Эта дуга окружности замыкает зазор между участками кривых KA1' и KA2'. Центр дуги окружности получают путем сдвига перегиба на расстояние а параллельно линии, соединяющей точки S1 и S2, в направлении тела К2. Это соответствует сдвигу (параллельному переносу) точки перегиба на вектор a → . Конечные точки получающейся в итоге дуги окружности граничат с границами участков кривых KA1' и KA2'. Таким образом, как величина, так и положение итоговой дуги окружности однозначно следуют из параметров, которые описывают точку перегиба как дугу окружности с радиусом, равным нулю.

Соответственно, способ согласно изобретению можно сформулировать следующим образом:

Предметом настоящего изобретения является способ создания двух тел K1 и K2, которые при равнонаправленном вращении с одинаковой скоростью вокруг двух расположенных параллельно друг другу на расстоянии a осей A1 и A2 всегда по меньшей мере в одной точке соприкасаются друг с другом, отличающийся тем, что в некоторой плоскости Е перпендикулярно осям вращения образуют профиль сечения тела K1 посредством непрерывной, на отдельных участках непрерывно дифференцируемой, замкнутой, выпуклой кривой p → , а профиль сечения тела K2 образуют из кривой p → в соответствии с отношением

q → = p → + a ⋅ n → ( p → ) + a →                       ( 1 )

причем

- в каждой точке кривая p → имеет радиус кривизны ρ, который меньше расстояния а или равен ему;

- для каждой точки кривой p → в пределах непрерывно дифференцируемого участка существует нормированный нормальный вектор n → ( p → ) длины 1, который в данной конкретной точке перпендикулярен касательной к кривой p → и указывает в направлении центра круга кривизны, принадлежащего к данной конкретной точке кривой p → ;

- a → представляет собой вектор, который проходит от точки пересечения S1 оси вращения A1 с плоскостью Е до точки пересечения S2 оси вращения A1 с плоскостью Е и имеет длину а,

- в случае перегиба в профиле сечения тела K1 профиль сечения тела K2 имеет дугу окружности, радиус которой соответствует межосевому расстоянию а, а угол которой соответствует тому углу, под которым встречаются друг с другом касательные к участкам кривых кривой p → в точке перегиба.

Точка пересечения S1 может лежать внутри замкнутой кривой p → или вне ее. Предпочтительно, чтобы точка пересечения S1 лежала внутри замкнутой кривой p → .

Замкнутая кривая p → может обладать зеркальной симметрией, центральной (точечной) симметрией или симметрией вращения. Если замкнутая кривая p → обладает зеркальной симметрией, то предпочтительно, чтобы точка пересечения S1 располагалась на оси симметрии. Если у замкнутой кривой p → имеется более одной осей симметрии, то предпочтительно, чтобы точка пересечения S1 располагалась в точке пересечения по меньшей мере двух осей симметрии кривой p → . Если замкнутая кривая p → обладает центральной симметрией, то целесообразно, чтобы точка пересечения S1 располагалась в центре симметрии. Если замкнутая кривая p → обладает симметрией вращения, то целесообразно, чтобы точка пересечения S1 располагалась в центре вращения профиля.

Если точка пересечения S1 располагается внутри или на кривой p → , то для всех точек на кривой p → максимальное расстояние до точки S1 равняется a, а минимальное расстояние составляет 0.

Кривую p → можно, например, непрерывно описать одной математической функцией. В качестве примеров следует назвать известные специалисту функции, как то: круговые, эллиптические, параболические или гиперболические функции. Кроме того, например, можно представлять функции в форме

p → = ( r 0 − f ( s ) ) ⋅ ( cos ( s ) sin ( s ) ) + ( x 0 y ) ,

в силу чего, в зависимости от формы функции f(s) при реализации шнековых элементов получается произвольно выбираемая щель между корпусом с радиусом r₀ и вращающимся шнековым элементом. f(s) может представлять собой линейную или квадратичную функцию s, гиперболическую функцию или экспоненциальную функцию.

Кроме того, следует назвать функции, значения которых определяются контрольными точками, как, например, B-сплайн-функции, функции Безье, рациональные функции Безье, а также неоднородные рациональные В-сплайны (NURBS). Функции Безье, рациональные функции Безье, NURBS предпочтительны, поскольку их часто применяют в конструировании с применением систем CAD (Computer Aided Design, САПР - системы автоматизированного проектирования), и там они служат для того, чтобы путем сдвига контрольных точек задавать произвольные формы в геометрически наглядном виде.

В качестве примера здесь следует привести функции Безье. Как известно, функции Безье имеют форму

C → ( t ) = ∑ i = 0 n B i , n ( t ) P → i ,

причем P → i - это координаты контрольных точек, а

B i , n ( t ) = ( n i ) t i ( 1 − t ) n − i

полином Бернштейна.

Рациональные функции Безье степени n, которые описаны, например, в книге М.S.Floater „Derivatives of rational Bezier curves". Comp. Aid. Geom. Design 9, 1992, 161-174 [4], как известно, имеют форму

P → ( t ) = ∑ i = 0 n B i , n ( t ) w i P → i ∑ i = 0 n B i , n ( t ) P → i

причем P → i представляет координаты контрольных точек функции, a w_i их весомость.

Особо предпочтительны квадратичные и кубические (т.е., где n=2 и n=3) функции Безье и кубические рациональные функции Безье.

Выкладки (выведение), необходимые для реализации способа, специалист может получить, применяя общеизвестные математические правила. Различные методы для рациональных функций Безье приведены, например, в [4]. Для расчета выведения целесообразно также применять компьютерную алгебраическую систему. Еще одна возможность состоит в том, чтобы аппроксимировать выведение, исходя из имеющихся численных данных, например, через расчет разностей. Такие способы известны специалисту и представлены, например, в книге Press, Teukolsky, Vetterling, Flannery: "Numerical Recipes in FORTRAN", 2nd edition, ISBN 052143064 X, начиная со стр.180 [5].

Кривую p → можно равным же образом описать на отдельных участках различными математическими функциями, причем функции на участках предпочтительно соответствуют функциям, упомянутым в предыдущем абзаце.

Особый случай описания математическими функциями по отдельным участкам представляет собой описание посредством дуг окружности. Возможно описать часть или всю кривую p → , а, соответственно, и часть или весь профиль сечения тела K1 через дуги окружности. Из отношения q → = p → + a ⋅ n → ( p → ) + a → следует, что в этом случае кривая q → и, соответственно, профиль сечения соответствующего телу K1 тела K2 составлен из дут окружности.

Если профили создают по отдельным участкам в соответствии со способом согласно изобретению, то соответствующие участки профилей тел K1 и K2 также могут меняться от участка с участком. В этом случае после предварительного задания участка p → n и вычисления соответствующего участка q → n предварительно задают участок кривой p → n + 1 , который по касательной переходит в q → n и в соответствии с (1) при замене S1 и S2 друг на друга (т.е., при использовании - a → вместо a → ) дает в результате участок кривой q → n + 1