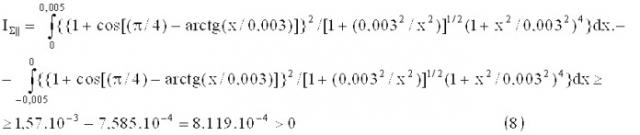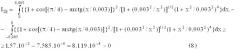Двигатель постоянного тока с косокруговыми обмотками

Двигатель постоянного тока с косокруговыми обмотками

Иллюстрации

Показать все

Реферат

Изобретение относится к электротехнике и может быть использовано для создания вращательного движения механической системы на постоянном токе без использования малонадежных элементов - коллекторов.

Намагничивание ферромагнетиков с большой коэрцитивной силой (магнитотвердые материалы) осуществляют в насыщающих магнитных полях или с помощью обмотки соленоида, через которую пропускают импульс однонаправленного тока от заряженных высоковольтных импульсных конденсаторов [1-3]. Ранее автором были предложены способы так называемого косокругового намагничивания ферромагнитных тороидов [4-5].

Термин «косокруговое намагничивание» впервые был введен автором заявляемого технического решения. Такое намагничивание ферромагнитного тороида возникает при его помещении в насыщающее постоянное или однонаправленное импульсное магнитное поле, которое образуется суперпозицией двух отдельно создаваемых магнитных полей - тороидального и соленоидального, ортогонально ориентированных друг к другу. При этом векторы намагниченности ферромагнитного тороида с прямоугольным поперечным сечением наклонены к плоскости грани тороида в одном направлении по кругу. Проекция любого такого вектора намагниченности на ось, ортогональную к плоскости грани тороида, определяется напряженностью соленоидального магнитного поля, а проекция вектора намагниченности (тангенциальная составляющая) на плоскость грани определяется напряженностью тороидального магнитного поля. Эти магнитные поля образуются соответствующими обмотками, включенными, например, последовательно, через которые пропускают однонаправленные импульсы насыщающего тока в процессе намагничивания ферромагнитного тороида или постоянный ток.

В том случае, если на тороиде расположена обмотка вокруг направляющей тороида, в нем возникает намагниченность, магнитные силовые линии представляют собой замкнутые окружности, расположенные внутри тороида, а направление магнитных силовых линий соответствует движению правовращающего буравчика. Такой постоянный магнит с внешними ферромагнитными телами практически не вступает в силовое взаимодействие, так как снаружи тороида внешнее силовое магнитное поле практически отсутствует. Если при этом ферромагнитный тороид разместить в охватывающий его соленоид, витки которого расположены осесимметрично к оси симметрии тороида, то последний намагничивается так, что на его верхней и нижней гранях возникают полюсы постоянного магнита N и S, причем направление магнитных силовых линий от северного полюса N к южному полюсу S во внешней среде также подчиняется правилу правовращающего буравчика (при движении свободных электронов в проводнике соленоида по часовой стрелке, как по виткам буравчика, его ввинчивание указывает направление магнитных силовых линий поступательным движением буравчика). Такие постоянные магниты используются для фокусировки электронных пучков в лампах обратной волны или, например, в электромагнитных динамиках. В результате одновременного наложения этих двух различных намагничивающих ферромагнитный тороид полей - тороидального и соленоидального - и образуется так называемое косокруговое намагничивание ферромагнитного тороида, который затем освобождается от намагничивающих его обмоток.

Тангенциальные составляющие двух намагниченных ферромагнитных тороидов, векторы намагниченности которых расположены взаимно встречно одноименными полюсами, кроме известного отталкивания таких намагниченных тороидов друг от друга вдоль оси их симметрии, совпадающей с проекциями векторов намагниченности, образованными действием намагничивающего соленоидального магнитного поля, будут образовывать вращательные моменты, образующиеся от воздействия тороидальных намагничивающих полей, причем действующие на эти тороиды вращательные моменты имеют противоположные знаки, как это указано в [7].

Заявляемое техническое решение основано на использовании взаимодействия статических магнитных полей с так называемой косокруговой конфигурацией (название введено автором). Как известно, магнитные поля постоянных магнитов распределены в пространстве таким образом, что всегда можно построить некоторую поверхность с непрерывной производной по координатам X, Y и Z, к которой магнитные силовые линии этого поля перпендикулярны. Однако в случае косокругового магнитного поля такую поверхность построить невозможно, как это станет ясно из дальнейшего рассмотрения. Поэтому косокруговое распределение в пространстве магнитного поля является принципиально новым видом магнитного поля.

Целью изобретения является создание нового типа магнитного двигателя постоянного тока с использованием косокруговой конфигурации ротор-статорного или ротор-роторного магнитных полей (в зависимости от конструктивного исполнения).

Указанная цель реализуется в заявляемом двигателе постоянного тока с косокруговыми обмотками, использующем встречно-косокруговое магнитное взаимодействие, отличающемся тем, что вращающиеся во взаимно противоположных направлениях относительно неподвижной оси два ротора, соосно установленные между собой, выполнены с обмотками, создающими встречно ориентированные косокруговые магнитные поля соответственно по правому и левому кругам, создаваемые постоянным током в этих обмотках, расположенных вблизи друг от друга, витки которых наклонены к плоскостям роторов, ортогональных неподвижной оси вращения роторов, и равномерно распределены по их кольцевым (тороидально подобным) объемам, а подсоединение этих обмоток к источнику постоянного тока через скользящие токосъемники осуществлено так, что образующиеся косокруговые магнитные поля являются взаимно встречными с одноименными магнитными полюсами.

Достижение поставленной цели объясняется возникновением вращательного момента между двумя соосно установленными роторами с косокруговыми магнитными полями по правому и левому кругам за счет известного эффекта отталкивания постоянных магнитов друг от друга, возрастающего при их сближении одноименными магнитными полюсами. В данном случае отталкивание происходит как вдоль оси симметрии тороидально подобных роторов, так и по всем касательным к их образующим. Токосъем в указанных вращающихся вместе с роторами обмотках осуществляется подключением их выводов к скользящим контактам кольцевых токосъемников, закрепленных изолированно и неподвижно на оси вращения роторов, которые связаны с источником постоянного тока. Такие обмотки автором названы косокруговыми, поскольку они распределены по кругу в кольцевом объеме, и сечения витков этих обмоток по всему кольцевому объему наклонены под некоторым ненулевым углом к неподвижной оси вращения роторов.

Изобретение понятно из представленных рисунков.

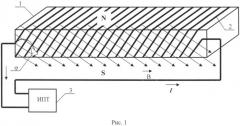
На рис.1 дана схема построения заявляемого двигателя, она содержит:

1 - ферровещество в форме параллелепипеда.

2 - обмотка, сечения витков которой наклонены под углом φ к плоской грани ферритового образца 1 с прямоугольным сечением,

3 - источник постоянного тока, образующий насыщающее магнитное поле для данного типа ферровещества.

В результате намагничивания ферромагнитного параллелепипеда 1 возникает его намагниченность, векторы которой наклонены по отношению к его плоской грани под углом φ (прямо-косая намагниченность). Этот рисунок поясняет принцип создания косокруговой намагниченности тороидального ферромагнетика - ферромагнитного кольца (тороида), если параллелепипедоидальный образец 1 превратить в тороидальный замыканием его концов между собой с образованием кольца.

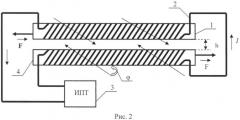
На рис.2 представлена схема силового взаимодействия двух одинаковых параллелепипедов ферровещества с подключенными к источнику постоянного тока их обмотками, как показано на рис.1, и расположенными вблизи друг от друга. На рис.2 показан дополнительно:

4 - дополнительный параллелепипед из ферромагнитного вещества с аналогичной обмоткой 2, которая также включена к источнику постоянного тока 3, но взаимно встречно обмотке 2 на параллелепипеде 1. Параллелепипеды 1 и 2 расположены вблизи друг от друга взаимно параллельно, а главные оси параллелепипедов (вдоль их длины) коллинеарны.

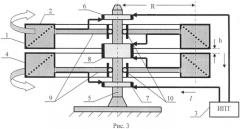
На рис.3 представлена одна из возможных моделей заявляемого двигателя с ротор-роторным косокруговым взаимодействием и содержит следующие элементы:

1 и 4 - два одинаковых ферромагнитных кольца с прямоугольным сечением,

2 - обмотки, одинаково выполненные на ферромагнитных кольцах 1 и 4 с наклоном сечений их витков под некоторым углом φ (не равным нулю) к плоским граням этих колец и включенные между собой по направлению тока в них взаимно встречно,

3 - источник постоянного тока,

5 - неподвижная ось вращения роторов на основе ферромагнитных колец 1 и 4,

6 - скользящий токосъемник первого ротора на ферромагнитном кольце 1 с обмоткой 2,

7 - скользящий токосъемник второго ротора на ферромагнитном кольце 2 с обмоткой 2,

8 - общий скользящий токосъемник для первого и второго роторов, соединяющий выводы

их обмоток 2,

9 - траверсы крепления ферромагнитных колец 1 и 4 с подшипниками качения,

10 - подшипники качения для обеспечения вращения первого и второго роторов относительно неподвижной оси 5 во взаимно противоположных направлениях.

Направления вращения первого и второго роторов указаны фигурными стрелками, расстояние между параллельно расположенными гранями ферромагнитных колец 1 и 4 равно h. В последовательно-встречно соединенных обмотках 2 протекает ток I, а его направление указано стрелками. Средний радиус ферромагнитных колец показан как R.

Этот рисунок поясняет работу двигателя на примере силового взаимодействия дифференциальных площадок на торцах первого и второго роторов, расположенных друг от друга на расстоянии h и имеющих косокруговое намагничивание с взаимно встречным расположением векторов намагниченности. При этом каждый из таких векторов образован суперпозицией магнитных полей - соленоидального магнитного поля Н_С и тороидального магнитного поля Н_Т, образующегося от протекающего в обмотках 2 постоянного тока I. Дифференциальный вектор силы расталкивания F первого и второго роторов на ферромагнитных кольцах 1 и 4 совпадает с направлением суммарного вектора напряженности H_Σ, модуль которого H Σ = [H C 2 + H T 2 ] 1 / 2 , где Н_С и Н_Т - векторы напряженности соответственно соленоидального и тороидального магнитных полей. Скалярная составляющая этого дифференциального вектора F в проекции на торцевую плоскость роторного ферромагнитного тороида 1 и равная F=Fcosφ, где ф=arctg[Н_С/Н_Т], является той движущей дифференциальной силой, которая составляет вращательный момент, величина которого равна произведению интеграла ∫dF по поверхности торца S ферромагнитного тороида 1 на средний диаметр R последнего (предполагается, что ферромагнитные тороиды являются одинаковыми по габаритам). На рис.2 и 3 указано расстояние h между торцами первого и второго роторов на ферромагнитных кольцах 1 и 4.

На рис.4 дана линейная развертка части взаимодействующих ферромагнитных колец 1 и 4 (тороидов) с косокруговым взаимодействием в линеаризованном представлении для доказательства возникновения ненулевого вращательного момента.

На рис.5 дан график распределения сил, действующих между доменной цепью одного тороида относительно доменных цепей другого тороида, полученный расчетным путем по программе MathCad и доказывающий возникновение вращательного момента в рассматриваемой паре намагниченных ферромагнитных колец 1 и 4.

Рассмотрим действие заявляемого устройства.

Прежде всего дадим представление о косокруговом распределении магнитного поля в пространстве декартовой системы координат. Пусть векторы предварительной намагниченности ферромагнитного тороида коллинеарны с осью Z, а плоскость торца последнего расположена параллельно плоскости XY декартовой системы координат. При намагничивании ферромагнитного тороида током подмагничивания I от регулируемого источника постоянного тока 3 соответствующие магнитные силовые линии в объеме тела ферромагнитного тороида располагаются по правому или левому кругам в зависимости от направления тока в обмотках подмагничивания 2 согласно известному «правилу буравчика». Поскольку наложение этих двух магнитных полей Н_C и Н_T, являющихся в любой точке ферромагнетика взаимно ортогональными, образует результирующее магнитное поле Н_Σ на основе принципа суперпозиции полей, то становится ясным, что все векторы результирующего магнитного поля Н_Σ наклонены к плоскости торца ферромагнитного тороида под некоторым углом ф=arctg[Н_C/Н_T], а наклон этих векторов вправо или влево от вертикали к плоскости торца определяется подмагничиванием ферромагнитного тороида соответственно по правому или левому кругам. Косокруговой характер образующегося магнитного поля связан с тем, что все точки исхода указанных векторов Н_Σ с поверхности торца распределены по его кольцевой поверхности. Учитывая эффект «вмороженности» магнитных силовых линий в домены ферромагнетика, имеющие сечение Δs в плоскости торца (поперечный размер домена порядка долей микрона), проекции векторов Н_Σ на плоскость торца ферромагнитного тороида для двух смежных доменов, расположенных на одной окружности (соосной тороиду), составляют между собой малый угол Δα_i=2π/n_i, где n_i - число магнитных доменов, размещенных вдоль данной окружности радиуса R_i. При расстоянии между доменами, равномерно распределенными в ферровеществе, равном Δr, число n_i для окружности радиуса R_i равно n_i=2πR_i/Δr. При этом R_MIN≤R_i≤R_MAX, где R_M1N и R_MAX - соответственно минимальный и максимальный радиусы ферромагнитного тороида. Следовательно, угол Δα_i=2π/n_i=Δr/R_i, а индекс i=1, 2, 3, …k, где k=(R_MAX-R_MIN)/Δr, то есть общее число групп магнитных силовых линий (доменных цепей), исходящих с плоскости торца ферромагнитного тороида площадью S, равно

k ∑ i = 1 k n i ≈ S / Δ s (при этом сечение домена Δs включает также и его окрестность). Векторы Н_Σ, исходящие из точек, расположенных на одном и том же луче с его началом, лежащим на оси Z (с центром ферромагнитного тороида в плоскости его торца), являются взаимно коллинеарными. Из указанного выше ясно, что не существует гладкой поверхности (с непрерывной производной по координатам X, Y и Z), которая удовлетворяет условию ортогональности к ней магнитных силовых линий. Поверхность, удовлетворяющая такому условию, в случае косокруговой намагниченности ферромагнитного тороида, является поверхностью с разрывами, то есть не отвечающей условию непрерывности производной по координатам X, Y и Z.

Как известно, суммарная сила F_s, действующая между полюсами с магнитными потоками Ф₁ и Ф₂ на расстоянии d=h/sinφ, то есть вдоль векторов H_Σ по всей плоскости S торца ферромагнитного тороида 1, где h - расстояние между торцами ферромагнитных тороидов 1 и 4, равна F_s=Ф₁Ф₂/4πµ₀d²=Ф₁Ф₂sin²φ/4πµ₀h². Магнитные потоки Ф₁ и Ф₂ определяются произведениями индукций ферромагнитных тороидов В=µ₀Н_Σ на площадь S торцов ферромагнитных тороидов, то есть Ф=µ₀H_ΣS [Вб], где µ₀=1,256*10^-6 Гн/м - абсолютная магнитная проницаемость вакуума, Н_Σ - напряженность магнитного поля на торцах магнитов [А/м], размеры S и d соответственно в [м²] и [м]. Сила F_s разлагается на нормальную F_⊥ и касательную F_|| составляющие, вычисляемые как F_⊥=Fsinφ и F_||=Fcosφ, где угол φ=arctg (Н_⊥/Н_||). Ясно, что с уменьшением расстояния h между торцами ферромагнитных тороидов квадратично возрастает сила F_s косокругового отталкивания. Возникающий вращательный момент М=F_sRcosφ=Ф₁Ф₂Rsin²φcosφ/4πµ₀h². Максимум вращательного момента достигается при ф*=0,955 рад, для которого функция sin²φcosφ*=0,385, и, следовательно, максимум вращательного момента равен Мах М=3,06 µ₀ R(НS/h)²*10^-2 [Дж], при условии равенства модулей магнитных потоков Ф₁ и Ф₂ тороидов 1 и 2. Произведение величин RS=π²R_MIN ⁵(λ+1)³(λ-1)²/2 по конструктивному параметру λ=R_MAX/R_MIN, где R_MAX и R_MIN - соответственно максимальный и минимальный радиусы ферромагнитных тороидов 1 и 4 [м], и при λ=1,25 имеем для максимального момента Мах М=0,107 µ₀ R_MIN ⁵(H_Σ/h)² [Дж]. Так, при Н_Σ=10 кА/м, h=0,005 м и радиусе R_MIN=0,1 м получим максимальный момент Мах М=5,35 Дж. Если скорость вращения роторов относительно оси 5 (рис.3) будет равна n=50 об/с, то наибольшая мощность заявляемого двигателя составит более 1,5 кВт при объеме двигателя около 0,02 м³. Как следует из полученной формулы, для Мах М увеличение мощности двигателя достигается увеличением диаметра ферромагнитных тороидов и их сближением между собой, а также выбором ферроматериала тороидов с высокими значениями намагниченности, например ферритов SmCo₃, имеющих энергетическое произведение (ВН)_max величиной 320 Тл.кА/м (40 млн. Гс.э) [1-2].

Отметим, что ферромагнитные тороиды с указанной предварительной намагниченностью с образованием полюсов N и S на их торцах широко применяются в различных областях техники, например, при производстве электродинамиков, ламп обратной волны, в ускорителях заряженных частиц (электронов и протонов), адронном коллайдере в ЦЕРН е и т.д., и методика создания таких магнитов с намагничиванием от источника тока 3 хорошо отработана.

Изменением тока подмагничивания I от регулируемого источника постоянного тока 3 можно регулировать мощность двигателя.

Использование взаимодействия статических магнитных полей при косокруговом намагничивании ферромагнитных тороидов 1 и 4 (рис.3) по правому и левому кругам требует доказательства возникновения вращательного момента одного тороида относительно другого.

Рассмотрим силовое взаимодействие хотя бы одного магнитного домена (доменной цепи), расположенного на поверхности одного ферромагнитного тороида 1 со всеми магнитными доменами (доменными цепями), расположенными на поверхности другого ферромагнитного тороида 4, как показано на рис.4. Если при таком рассмотрении окажется, что результирующая касательная сила, приложенная к одному из тороидов (обладающих вращательной подвижностью - тороиду 4, при неподвижно закрепленном тороиде 1) со стороны другого, будет не равна нулю, то такое же точно рассмотрение будет правомерным и для всех других доменов, и парциальные силы будут складываться, создавая совокупный вращательный момент. Для такого рассмотрения достаточно взять какие-то части ферромагнитных тороидов 1 и 4 и представить их в виде эквивалентной линейной конструкции, как показано на рис.4. Пусть расстояние между поверхностями тороидов 1 и 4 равно h, а угол наклона центральных (осевых) силовых линий доменов относительно плоскостей соответствующих тороидов равен φ, и для доменов А тороида 1 и В тороида 4 осевые силовые линии взаимно встречно направлены. Расстояние между оппозитно расположенными доменами А и В равно, как нетрудно понять, r₀=h/sinφ. Расстояние между доменами А и С, когда домен С расположен относительно вертикальной оси симметрии, проходящей через домен А, на текущем расстоянии x в пределах - L/2≤x≤L/2, равно r(x)=(h²+х²)^1/2. Важно иметь в виду при расчетах наличие диаграммы направленности элементарного прямого постоянного магнита, каковым является ориентированный домен [3].

Эту диаграмму направленности следует определить с учетом установленного факта, что напряженность магнитного поля вдоль оси магнита Н_|| вдвое выше, чем поперек этой оси H_⊥. Этому известному условию удовлетворяет диаграмма вида Н(α)=Н_||(1+cosα)/2, где α - угол меду исследуемым направлением на домен А и осью симметрии прямого магнита (домена С). Так, при α=0 имеем Н(0)=Н_||, а при α=π/2 имеем Н(π/2)=H_||/2=H_⊥. Угол α для произвольно расположенного домена С на расстоянии x относительно вертикальной оси симметрии (при x=0) находится как α=φ+arctg(|x|/h) - для интервала по x в пределах - L/2≤x≤0, то есть при отрицательных значениях x, и α=φ-arctg(Ч/h) - для интервала 0≤x≤L/2, то есть для положительных значений x.

Как известно, если магнитный момент домена обозначить как М, то напряженность магнитного поля Н(r) на расстоянии r(x) под углом α находится согласно выражению:

H(x) = (H( α )/H || ) M / 2 π μ 0 r ( x ) 3 = ( 1 + cos α ) M / 4 π μ 0 ( h 2 + x 2 ) 3 / 2 = = [ 1 + cos ( ϕ − a r c t g ( x / h ) ) ] M / 4 π μ 0 ( h 2 + x 2 ) 3 / 2 .                                                                                                           ( 1 )

Поскольку домен А «видит» домен С под тем же углом α (так как плоскости разверток 1 и 4 являются взаимно параллельными), то сила взаимодействия между двумя доменами А и С вдоль направления соединяющего их отрезка г(х) равна:

F ( x ) = Ф 1 Ф 2 / 4 π μ 0 ( h 2 + x 2 ) ,                                   ( 2 )

где Ф₁=Ф₂=µ₀qH(x) - магнитный поток с площадок q доменов А и С, и тогда:

F(x) = μ 0 q 2  Í(õ) 2  / 4  π  (h 2 + õ 2 ) = = q 2  [1 + cos ( ϕ  - arctg (õ / h))] 2  M 2 / 64  π 3 μ 0  d  8  (1 + õ 2 / h 2 ) 4                            (3)

Нетрудно понять, что в левой половине от вертикальной оси симметрии, то есть в промежутке - L/2≤x≤0 возникают силы торможения, а в правом, для 0≤x≤L/2, - силы ускорения элемента 1 в направлении фигурной стрелки на рис.4.

Эти силы торможения и ускорения F(x)_|| являются проекциями сил F(x) на горизонтальную плоскость. Проекции сил F(x) на эту плоскость равны F(x)_||

F(x) || = F(x) cos [arctg (h/ x)] = F(x) / [1 + (h / x)2] 1/2 .                          (4)

Обозначая постоянный множитель k=q²M²/64π³µ₀h⁸=const(x) с размерностью этого коэффициента в ньютонах, получим из (3)

F ( x ) | | = k [ 1 + cos ( φ − a r c t g   ( x / h ) ) ] 2 / [ 1 + ( h / x ) 2 ] 1 / 2 ( 1 + x 2 / h 2 ) 4 = k ψ ( x ) .                   ( 5 )

Постоянный множитель k нас не интересует, и при интегрировании мы его можем опустить, проверив, чему будет равен интеграл от ψ(x) по всему промежутку - L/2≤x≤L/2, поскольку нас интересуют только касательные составляющие сил F(x). Тогда получим распределение безразмерных относительных сил ψ(x) на длине L в виде:

ψ ( õ) = [1 + cos( ϕ -arctg(x/h))] 2 /[1 + (h 2 + x 2 )] 1/2 (1 + x 2 /h 2 ) 4                           ( 6 )

График функции ψ(x) представлен на рис.5.

Площадь под графиком в его левой части существенно меньше площади под графиком в его правой части, что означает, что относительная сила ускорения больше относительной силы торможения. При этом равнодействующая этих сил не равна нулю, и ферромагнитный тороид 4 с косокруговым намагничиванием будет вращаться относительно неподвижного ферромагнитного тороида 1 с встречным косокруговым намагничиванием против часовой стрелки. Если первый и второй роторы (рис.3) могут свободно вращаться относительно неподвижной оси 5, то они будут вращаться во взаимно противоположных направлениях.

Примечание Построение графика по программе MathCad привело к необходимости переобозначений: h=Δ, φ=ф и x=β (по данным примененного шрифта на этой программе).

Для нахождения суммарной относительной силы I_Σ|| необходимо проинтегрировать функцию ψ(x) по всему промежутку L, задав известные величины h, L и φ. Задача решается корректно при условии h<L, что позволяет провести линеаризацию элементов 1 и 4, для упрощения расчетов (вместо части концентрических окружностей использовать параллельные прямые).

I Σ | | = ∫ − L / 2 L / 2 { [ 1 + cos ( ϕ − a r c t g ( x / h ) ) ] 2 / [ 1 / ( h + ( h 2 / x 2 ) ] 1 / 2 ( 1 + x 2 / h 2 ) 4 } d x .             ( 7 )

При указанных на графике величинах h=0,003 м (Δ) и φ=π/4(ф) для промежутка L=0,01 м интегрированием (7) получаем I_Σ:

I Σ | | = ∫ 0 0,005 { { 1 + cos [ ( π / 4 ) − a r c t g ( x / 0,003 ) ] } 2 / [ 1 + ( 0,003 2 / x 2 ) ] 1 / 2 ( 1 + x 2 / 0,003 2 ) 4 } d x .   −         − ∫ − 0,005 0 { { 1 + cos [ ( π / 4 ) − a r c t g ( x / 0,003 ) ] } 2 / [ 1 + ( 0,003 2 / x 2 ) ] 1 / 2 ( 1 + x 2 / 0,003 2 ) 4 } d x   ≥         ≥ 1,57.10 − 3 − 7,585.10 − 4 = 8.119.10 − 4 > 0                                                                                                                                                 ( 8 )

Знак больше или равно установлен, так как первый интеграл в (8) до конца не вычислен (можно было задать больший верхний предел, что усматривается из графика на рис.5). Из расчета следует, что относительная сила ускорения больше силы торможения в 1,57.10^-3/7,585.10^-4=2,09 раза!

Все остальные домены А на ферромагнитном тороиде 1 ведут себя точно так же. Их число определяется площадью грани S_ГP, отнесенной к площади полюса домена q, и число доменов n=S_ГP/q весьма велико. Так, если q=10^-10 м², а площадь грани тороида S_ГР=10 м². то n=10⁶ и относительная результирующая сила nI_Σ||=811,9, и это число надо умножить на коэффициент k=q²М²/64π³µ₀d⁸ для вычисления полной касательной силы, воздействующей на тороид 4, которая равна:

F Σ || = (q S ГР  М 2 / 64  π 3   μ 0  h 8 ) I Σ || ,        ãäå I Σ || = f (I) .                                (9)

ВЫВОД: В предложенном устройстве возникает вращательный момент.

Таким образом, обосновано теоретически возникновение вращательного момента в заявляемой паре ферромагнитных тороидов с встречным косокруговым намагничиванием, обращенных друг к другу одноименными полюсами.

Вращательный момент возникает за счет протекания токов в обмотках 2 (рис.3), намотанных указанным выше образом на этих тороидах, что согласуется с законом сохранения и превращения энергии, и такая система не является изолированной.

Рассмотренный тип двигателя постоянного тока не использует в своем составе коллектора, присущего известным двигателям постоянного тока. Вместо коллектора в нем использованы кольцевые электроды со скользящими контактами, что повышает надежность функционирования двигателя. Наличие в известных двигателях коллекторов вызывает искрение на них, поскольку при работе двигателей происходит непрерывно действующий разрыв в одних цепях и переключение тока на другие цепи (части обмоток роторов этих двигателей), что ускоряет износ рабочей поверхности коллекторов. Наличие кольцевых скользящих контактов не вызывает практически никакого искрения, и ток в обмотках 2 не прерывается во времени, что увеличивает существенно срок службы таких скользящих контактов. Такой двигатель не создает радиопомех.

Рассмотренная модель двигателя с двумя вращающимися роторами может быть заменена на модель «статор-ротор», для чего один из роторов выполняют неподвижным, и он становится статором, а ось вращения жестко скрепляется с другим ротором и передает в нагрузку вращательный момент, как это характерно для всех известных электрических двигателей. При этом в двигателе используется только два скользящих токосъемника вместо четырех, как в рассмотренной модели. Такая конструкция является аналогом заявленной, но более простой, чем рассмотренная, и может найти широкое практическое применение в промышленности и в бытовой технике.

Литература

1. Преображенский А.А., Биширд Е.Г. Магнитные материалы и элементы, 3 изд., М., 1986.

2. Февралева И.Е. Магнитотвердые материалы и постоянные магниты, К., 1969.

3. Постоянные магниты. Справочник. М., 1971.

4. Меньших О.Ф. Способ косокругового намагничивания ферромагнитного тороида. Патент РФ №2391730, опубл. в бюлл. №16 от 10.06.2010.

5. Меньших О.Ф. Способ косокругового намагничивания ферромагнитного тороида. Патент РФ №2392681, опубл. в бюлл. №17, от 20.06.2010.

6. Меньших О.Ф. Способ намагничивания ферромагнитного тороида. Патент РФ №2451351, опубл. в бюлл. №14, от 20.05.2012.

7. Меньших О.Ф. Прибор для измерения силового взаимодействия ферромагнитных тороидов. Патент РФ №2405164, опубл. в бюлл. №33, от 27.11.2010.

Двигатель постоянного тока, содержащий два соосно установленных на некотором расстоянии друг от друга ферромагнитных тороида, способных свободно вращаться друг относительно друга, отличающийся тем, что ферромагнитные тороиды снабжены косокруговыми обмотками, включенными к источнику постоянного тока через скользящие контакты на неподвижной оси так, что создают встречно ориентированные косокруговые магнитные поля по правому и левому кругам.