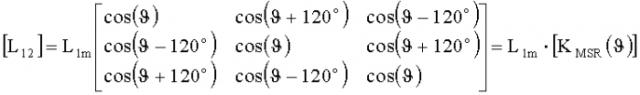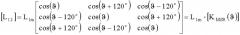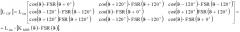Способ векторного управления скоростью вращения трехфазной машины

Способ векторного управления скоростью вращения трехфазной машины

Иллюстрации

Показать все

Реферат

Изобретение относится к электротехнике и может быть использовано в системах векторного управления скоростью вращения асинхронного электродвигателя, синхронного электродвигателя, машины двойного питания, в том числе в системах бездатчикового управления скоростью вращения и системах прямого управления моментом вращения.

Известен способ управления асинхронным электродвигателем, в котором асинхронный двигатель управляется путем регулирования выходного напряжения инвертора, преобразующего постоянный ток в переменный с регулированием частоты при регулируемом напряжении и регулированием частоты при постоянном напряжении за счет изменения глубины модуляции, которое выполняется по команде на изменение намагничивающей составляющей тока в первичной обмотке асинхронного двигателя, на который подается напряжение от инвертора, и по команде на изменение компоненты напряжения, которые формируются в соответствии с упомянутыми соответствующими компонентами и выполняются в соответствии с командой на изменение моментообразующей составляющей тока статора. Устройство, реализующее способ, содержит преобразователь полярных координат, преобразующий векторы напряжения в амплитуду и фазу этого результирующего вектора напряжения статора, преобразователь координат векторов тока, на вход которого поступают измеряемые датчиками токов три выходных тока ШИМ-инвертора (токи статора). Преобразователь координат преобразует последние по матричной формуле преобразования координат в соответствии с сигналом угла смещения в компоненту намагничивающей составляющей тока в системе координат вращающегося магнитного поля и в компоненту моментообразующей составляющей тока статора. С помощью системы регулирования в устройстве осуществляется уменьшение разности между заданными значениями величин и вычисленными по показаниям датчиков тока и напряжения значениями этих величин (RU №2193814, МПК Н02Р 21/00, опубл. 7.11.2002).

Недостатком способа является неточность системы регулирования по причине использования преобразования над векторами для трехфазных токов и напряжений статора в двухфазную ортогональную систему координат, в котором не учитывается тип обмоток статора конкретного электродвигателя и связанное с этим несинусоидальное распределение магнитной индукции в воздушном зазоре машины. Другим недостатком является то, что не учитывается распределенный характер токов ротора, индуцированных токами статора, что приводит к невысокой точности регулирования асинхронного двигателя в динамических режимах разгона и ускорения.

Известны способы векторным управлением электроприводами переменного тока (Виноградов А.Б. Векторное управление электроприводами переменного тока: Учебное пособие / ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина» - Иваново, 2008 г. - с.3-16), характеризующиеся следующими признаками:

- широко применяется метод преобразования координат с целью упрощения решения задач анализа и синтеза процессов в машинах переменного тока;

- прямое и обратное преобразование векторов токов и напряжений статора из неподвижной относительно статора трехфазной системы координат в неподвижную относительно статора двухфазную ортогональную систему координат с использованием векторно-матричной формы записи преобразования или эквивалентных этому преобразованию выражений;

- переход от неподвижной системы координат к вращающейся системе координат, повернутой на угол смещения координатных систем. Ортогональные системы координат, ориентированные по одному из векторов машины.

Наиболее широкое распространение в системах векторного управления получил способ ориентации переменных по вектору потокосцепления ротора. Часто такой способ называют ориентацией по полю (Виноградов А.Б. Векторное управление электроприводами переменного тока: Учебное пособие / ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина» - Иваново, 2008 г. - с. 191). При составлении уравнений асинхронной машины в пособии введено допущение: « пренебрежение высшими пространственными гармониками магнитного поля, то есть распределение магнитного поля каждой из обмоток вдоль окружности ротора и статора принято синусоидальным».

Недостатком описанного способа является неточность системы регулирования по причине использования преобразования над векторами на комплексной плоскости для трехфазных токов и напряжений статора в двухфазную ортогональную систему координат, в котором не учитывается тип обмоток статора конкретного электродвигателя и не учитывается связанное с этим несинусоидальное распределение магнитной индукции в воздушном зазоре машины.

Известны способы управления трехфазной машиной, используемые в асинхронных двигателях (Усольцев А.А. Частотное управление асинхронными двигателями: Учебное пособие - СПб: СПбГУ ИТМО, 2006, - раздел 2, с.50-70; рис.2.23 с.60; рис.2.31. с.69). Введено понятие обобщенного пространственного вектора. Синусоидальность распределения магнитодвижущей силы в зазоре машины позволяет представить магнитодвижущую силу или пропорциональные им токи обобщенным пространственным вектором на плоскости, перпендикулярной оси ротора машины. Под обобщенным вектором понимается вектор, проекции которого на оси фазных обмоток в любой момент времени равны мгновенным значениям фазных величин, представляемых этим вектором. Для упрощения математических операций координаты точек на любой плоскости, операции построения обобщенного вектора можно объединить в комплексные числа. Согласно способу для прямого векторного управления моментом вращения асинхронного двигателя определяются вектор потокосцепления статора и электромагнитный момент асинхронного двигателя. Затем модуль вектора и электромагнитный момент сравниваются с заданными значениями потокосцепления статора и электромагнитного момента асинхронного двигателя. После чего с помощью компараторов, называемых релейными регуляторами, формируются логические сигналы ошибки. Для управления модулем потокосцепления используют релейный регулятор с гистерезисом, а для управления моментом - релейный регулятор с гистерезисом и зоной нечувствительности. На основании сигналов этих регуляторов и информации о положении вектора потокосцепления на плоскости базовых векторов выбирают такую очередную комбинацию состояний ключей инвертора, при которой будет сформирован базовый вектор напряжения, уменьшающий отклонение от заданных значений. В результате работы системы регулирования модуль потокосцепления статора и электромагнитный момент асинхронного двигателя будут постоянно находиться в зоне допустимого отклонения от заданного значения.

Недостатком известного способа является неточность регулирования, связанная с использованием преобразования над векторами на комплексной плоскости для преобразования трехфазных токов и напряжений статора, магнитных потоков статора и ротора в проекции результирующих векторов на ортогональные оси системы координат без учета влияния типа обмоток статора конкретного электродвигателя на распределение магнитной индукции в воздушном зазоре машины и на процессы регулирования скорости вращения электродвигателя.

Известен способ, использованный в системе асинхронного электропривода с векторным управлением без датчика скорости (Козярук А.Е. Современное и перспективное алгоритмическое обеспечение частотно-регулируемых электроприводов / А.Е. Козярук, В.В. Рудаков, /Под ред. А.Г. Народицкого. - СПб.: Санкт-Петербургская Электротехническая компания, 2004. - с.30-39, с.46-48, с.66-70, с.80-85, с.82, рис.30), в котором используются выражения для преобразования трехфазных токов статора в ортогональную двухфазную систему, являющихся преобразованиями векторов на комплексной плоскости для идеализированной машины, имеющей синусоидальное распределение магнитной индукции в зазоре машины независимо от типа обмоток статора. Аналогичные преобразования используются для напряжений статора, магнитных потоков статора и ротора.

Недостатком данного способа является неточность регулирования, связанная с использованием преобразования над векторами на комплексной плоскости для преобразования трехфазных токов и напряжений статора, магнитных потоков статора и ротора в проекции обобщенных векторов на ортогональные оси координат без учета влияния типа обмоток статора конкретного электродвигателя на распределение магнитной индукции в воздушном зазоре машины, на формирование момента вращения и на процесс регулирования скорости вращения.

Наиболее близким техническим решением является способ векторной ориентации тока электромеханического преобразователя энергии, в котором измеряют ток, преобразуют его в двухфазную систему координат, измеряют напряжение статора, преобразуют его в двухфазную систему координат, определяют амплитуды и фазы тока и напряжения, затем вычисляют потокосцепление статора в двухфазной системе координат, вычисляют фазы и амплитуды потокосцепления статора, ротора, затем вычисляют нормированные с единичной амплитудой косинусные и синусные функции фаз указанных векторов и синфазные и ортофазные токи и углы фазового сдвига вектора тока относительно любого из указанных векторов. Дополнительно вычисляют электромагнитный момент электромеханического преобразователя (RU 2141720, МПК Н02Р 21/00, опубл. 20.11.1999).

Недостатком способа является неточность расчетов по причине использования преобразования над векторами на комплексной плоскости для преобразования трехфазных токов и напряжений статора в двухфазную ортогональную систему, в котором не учитывается тип обмоток статора конкретного электродвигателя.

Технический результат заключается в повышении точности регулирования скорости вращения и момента вращения трехфазной машины за счет более точного учета параметров конкретной машины при преобразовании координат, которое используется в системе управления для векторов токов, напряжений и потокосцеплений.

Технический результат достигается тем, что измеряют ток трехфазной машины, преобразуют его в двухфазную систему координат, измеряют напряжение статора трехфазной машины, преобразуют его в двухфазную систему координат, определяют амплитуды и фазы тока и напряжения, затем вычисляют потокосцепление статора в двухфазной системе координат, вычисляют фазы и амплитуды потокосцепления статора, ротора, затем вычисляют нормированные с единичной амплитудой косинусные и синусные функции фаз указанных векторов и синфазные и ортофазные токи и углы фазового сдвига вектора тока относительно любого из указанных векторов, дополнительно вычисляют электромагнитный момент трехфазной машины. Преобразование фазных токов, магнитных потоков и напряжений статора в результирующие векторы токов, магнитных потоков и напряжений статора и ротора и преобразование в их проекции на ортогональные оси координат производят с умножением на соответствующие поправочные коэффициенты элементов матриц преобразований векторов или с умножением на соответствующие поправочные коэффициенты элементов эквивалентных выражений матрицам преобразований векторов для идеализированной модели машины, преобразование между векторами статора и ротора производят с умножением элементов матриц преобразований векторов на соответствующие поправочные функций от угла смещения ротора относительно статора или с умножением на соответствующие поправочные функций от угла смещения ротора относительно статора элементов эквивалентных выражений матрицам преобразований векторов для идеализированной модели машины, причем упомянутые поправочные коэффициенты и поправочные функции создают согласно с распределением магнитной индукции вдоль воздушного зазора конкретной машины в соответствии с типом обмоток статора и обмоток ротора этой машины.

На фиг.1 приведено распределение м.д.с. (индукции) по пазам статора от действия тока обмотки фазы А статора для трехфазной петлевой двухпериодной обмотки с укороченным шагом (Z=36, p=2, m=3, y=7, q=3).

На фиг.2 построены графики по расчетным значениям из табл.1 для изменения проекций магнитного потокосцепления фазы А статора на пространстве одного полюсного деления в зависимости от угла смещения 0 относительно оси обмотки А статора (на графике - смещения привязаны к пазам статора).

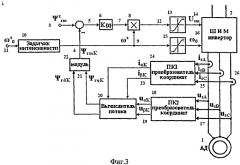
На фиг.3 изображена схема системы векторного управления асинхронного двигателя.

В табл.1 приведены результаты расчета поправочных коэффициентов и поправочных функций к матрицам преобразований магнитных потоков, токов и напряжений трехфазной машины.

Сущностью предлагаемого способа является введение поправочных коэффициентов и поправочных функций к матрицам преобразований магнитных потоков, токов и напряжений трехфазной машины.

Для этого:

1. Создание поправочных коэффициентов и поправочных функций отражено в табл.1. Расчеты проекций магнитного потокосцепления фазы А статора асинхронной машины на полюсное пространство машины в зависимости от угла смещения относительно оси обмотки А статора для трехфазной петлевой двухпериодной обмотки с укороченным шагом (Z=36, p=2, m=3, у=7, q=3) выполнены согласно табл.1. Графики фиг.2. выполнены согласно табл.1. и позволяют определить поправочную функцию КАа(θ) к функции cos(θ) изменения проекции вектора магнитного потокосцепления обмотки по углу смещения относительно оси этой обмотки, которая используется в матрице [L₁₂]=L_1m·[K_MSR(ϑ)] для идеализированной модели машины.

Для взаимоиндуктивных связей обмоток статора и ротора в преобразовании векторов на комплексной плоскости ПВК-ПГ (для идеализированной машины) используют матрицу -

[ L 12 ] = L 1 m [ cos ( ϑ ) cos ( ϑ + 120 ∘ ) cos ( ϑ − 120 ∘ ) cos ( ϑ − 120 ∘ ) cos ( ϑ ) cos ( ϑ + 120 ∘ ) cos ( ϑ + 120 ∘ ) cos ( ϑ − 120 ∘ ) cos ( ϑ ) ] = L 1 m ⋅ [ K M S R ( ϑ ) ] .

В предлагаемом модифицированном способе преобразования векторов на комплексной плоскости (М-ПВК) используются поправочные функции KAa(ϑ)=FSR(θ) к элементам K_MSR(ϑ) матрицы преобразований [L₁₂] в преобразовании векторов на комплексной плоскости ПВК-ПГ (для идеализированной машины) -

[ L 12 F ] = L 1 m [ cos ( ϑ ) ⋅ F S R ( ϑ + 0 ∘ ) cos ( ϑ + 120 ∘ ) ⋅ F S R ( ϑ + 120 ∘ ) cos ( ϑ − 120 ∘ ) ⋅ F S R ( ϑ − 120 ∘ ) cos ( ϑ − 120 ∘ ) ⋅ F S R ( ϑ − 120 ∘ ) cos ( ϑ ) ⋅ F S R ( ϑ + 0 ∘ ) cos ( ϑ + 120 ∘ ) F S R ( ϑ + 120 ∘ ) cos ( ϑ + 120 ∘ ) F S R ( ϑ + 120 ∘ ) cos ( ϑ − 120 ∘ ) ⋅ F S R ( ϑ − 120 ∘ ) cos ( ϑ ) ⋅ F S R ( ϑ + 0 ∘ ) ] = = L 1 m ⋅ [ K M S R ( ϑ ) ⋅ F S R ( ϑ ) ] .

Здесь FSR(ϑ) - поправочная функция к элементам матрицы взаимных индуктивностей [L₁₂] между обмотками статора и ротора идеализированной модели машины.

Проекции магнитного потока соответствуют потокам, прошедшим через воздушный зазор, т.е. потокам взаимной индукции между обмотками статора или между обмотками ротора. Поэтому значения функции КАа(θ) для углов смещения θ могут быть использованы как поправки KSS к коэффициентам [K_MSS] матрицы взаимных индуктивностей между обмотками статора [L₁]=L_1m([1]·k_1σ+[K_MSS]) для образования модифицированной матрицы [L_1K]=L_1m([1]·k_1σ+[K_MSS]·KSS). Поправочная функция FSR(θ) применяется к элементам матрицы взаимных индуктивностей обмоток статора и ротора [L_12F=L_1m·[K_MSR(ϑ)] для образования модифицированной матрицы взаимных индуктивностей между обмотками статора и ротора [L_12F]=L_1m·[K_MSR(ϑ)·FSR(θ)]. Поправочная функция KAa(θ=FSR(θ) (верхний график фиг.2. ) показывает (для рассматриваемого типа намотки), что магнитный поток фазы А статора проектируется на другие направления обмоток статора и ротора довольно близко к функции cosθ, соответствующей идеализированной модели машины. Коэффициент поправки KSS к элементам K_MSS матрицы взаимоиндуктивной связи между обмотками статора, например, для обмотки фазы А статора с обмоткой фазы В статора при сдвиге на 120°(2π/3)[рад] KSS=FSR(θ)=FSR(2π/3) составит всего 0,473/0,5=0,946. Аналогичные расчеты проведены и для двух других типов обмоток -двухслойной обмотки при Z=24, 2р=4, q=2 и для шаблонной обмотки вразвалку при Z=24. p=2, q=4, τ=12, у=10(1-11). Эти расчеты подтверждают выводы, полученные выше для анализа магнитных потокосцеплений двухпериодной обмотки с укороченным шагом при Z=36, y=7, τ=9, 2р=4. Последняя имеет наилучшее из анализированных обмоток распределение м.д.с., приближающееся к идеальному - синусоидальному. Для двухслойной обмотки при Z=24, 2р=4, q=2 поправочный коэффициент составляет KSS=FSR(2π/3)=0,842, а для шаблонной обмотки вразвалку при Z=24. p=2, q=4, τ=12, у=10(1-11) поправка составляет KSS=FSR(2π/3)=0,889. Для расчетной поправочной функции КАа(θ) на фиг.2. создана функция приближения - КАа(θ)=FSR(θ)=1-0,055·sin(θ)·sgn(sin(θ)) (для двухпериодной обмотки с укороченным шагом при Z=36, y=7, τ=9, 2р=4). Функции приближения могут быть любыми другими, а также возможно использование табличных функций.

2. Алгоритм применения поправочных коэффициентов и поправочных функций.

Перечень условных обозначений величин:

(α,β) - неподвижная относительно статора двухфазная ортогональная система координат, ориентированная по положению обмотки фазы А статора;

(i_sA i_sB i_sC) - мгновенные значения токов фаз. А, В, С статора;

КАВ, КβВ=KβС=Kβ - поправочные коэффициенты KSS к формулам преобразования трехфазной системы токов статора в двухфазную ортогональную систему токов статора для идеализированной модели двигателя;

i → s K ( α β ) - уточненный обобщенный вектор токов статора в системе

координат (α,β);

i_αK, i_βK - уточненные проекции обобщенного вектора тока статора на ортогональные оси системы координат (α,β);

i_sdK, i_sqK - уточненные проекции обобщенного вектора тока статора на ортогональные оси системы координат (d,q);

(u_sA u_sB u_sC) - мгновенные значения фазных напряжений трехфазной системы обмоток статора;

u → s K ( α β ) - уточненный обобщенный вектор напряжений статора в системе координат (α,β);

(u_αK, u_βK) - уточненные проекции обобщенного вектора напряжений статора на неподвижную относительно статора ортогональную двухфазную систему координат (α,β);

L_m, L_S, L_r - индуктивности (соответственно) намагничивания, статора, ротора, приведенные к цепи статора;

σ - коэффициент рассеяния магнитной цепи двигателя,

σ = 1 − L m 2 / ( L s ⋅ L r ) ;

R_s, R_r - активное сопротивления статора, активное сопротивление ротора, приведенное к цепи статора;

T_r - постоянная времени цепи ротора, T_r=L_r/R_r;

Ψ_rαK, Ψ_rβK - уточненные проекции обобщенного вектора магнитного потокосцепления ротора на неподвижную относительно статора ортогональную двухфазную систему координат (α,β);

Ψ_rmK - уточненный модуль обобщенного вектора магнитного потокосцепления ротора;

γ_K - уточненный пространственный угол между мгновенным положением вектора магнитного потокосцепления ротора и осью α системы координат (α,β),

(d,q) - ортогональная система координат, ориентированная относительно магнитного потокосцепления ротора (относительно магнитного потока машины в воздушном зазоре);

z_p - число пар полюсов статора;

М - момент вращения двигателя.

2.1. Преобразование фазных токов статора в проекции результирующего вектора тока статора на ортогональные оси координат.

Преобразование для трехфазной системы токов (i_sA i_sB i_sC) обмоток статора в эквивалентную, неподвижную относительно статора двухфазную ортогональную систему координат (α,β), получит вид -

i_αK=i_sA+(-0,5)·KAB·(i_sB+i_sC);

i β K = ( − 3 2 ) ⋅ K β B ⋅ i s B + ( + 3 2 ) ⋅ K β C ⋅ i s C = 3 2 ⋅ K β ⋅ ( − i s B + i s C ) ;

i → s K ( α β ) = i α K + j i β K

где КАВ, КβВ=КβС=Кβ - поправочные коэффициенты KSS к формулам преобразования трехфазной системы токов статора в двухфазную ортогональную систему токов статора для идеализированной модели двигателя.

(В качестве примера, здесь приведены поправочные коэффициенты из в табл.1 - КАВ=0.946, Кβ=0.942).

2.2. Преобразование фазных напряжений статора в проекции обобщенного вектора напряжений статора на ортогональные оси координат.

Преобразование трехфазной системы фазных напряжений обмоток статора (u_sA u_sB u_sC) в проекции результирующего (обобщенного) вектора напряжений статора (u_αK, u_βK) на эквивалентную, неподвижную относительно статора ортогональную двухфазную систему координат (α,β), получит вид -

u_αK=u_sA+(-0,5)·KAB·(u_sB+u_sC);

u β K = ( − 3 2 ) ⋅ K β B ⋅ u s B + ( + 3 2 ) ⋅ K β ⋅ ( − u s B + u s C ) ;

u → s K ( α β ) = u α K + j u β K

где KAB, KβB=KβС=Кβ - поправочные коэффициенты KSS к формулам преобразования трехфазной системы напряжений статора к двухфазной ортогональной системе напряжений статора (α,β) для идеализированной модели двигателя.

(В качестве примера, здесь приведены поправочные коэффициенты из табл.1 - КАВ=0.946, Кβ=0.942).

2.3. Вычисление проекции магнитного потокосцепления ротора на ортогональные оси координат (α,β) выполняется согласно выражениям

ψ r α K ( t ) = ψ r α K = L m L r [ ∫ 0 t ( u α K − R s i α K ) d t − σ L s i α K ] ;

ψ r β K ( t ) = ψ r β K = L m L r [ ∫ 0 t ( u β K − R s i β K ) d t − σ L s i β K ] .

2.4. Вычисление модуля магнитного потокосцепления ротора

ψ r m K ( t ) = ψ r m K = ψ r α K 2 + ψ r β K 2 .

2.5. Вычисление угла смещения γ_K от системы координат (α,β) к системе координат (d,q), где γ_K - уточненный пространственный угол между мгновенным положением вектора магнитного потокосцепления ротора и осью α системы координат (α,β), производится через тригонометрические функции

γ_K=arctg(ψ_rβK/ψ_rαK); cosγ_K=ψ_rαK/ψ_rmK; sinγ_K=ψ_rβK/ψ_rmK.

2.6. Переход от системы координат (α,β) к системе координат (d,q).

Вычисление проекций магнитного потокосцепления ротора в системе координат (d,q)

ψ_rdK=ψ_rαKcosγ_K+ψ_rβKsinγ_K;

ψ_rqK=-ψ_rαKsinγ_K+ψ_rβKcosγ_K.

2.7. Переход от системы координат (α,β) к системе координат (d,q).

Вычисление проекций тока статора в системе координат (d,q)

i_sdk=i_sαKcosγ_K+i_sβKsinγ_k;

i_sqk=-i_sαKsinγ_k+i_sβKcosγ_K.

2.8. Вычисление момента вращения

M = 3 2 Z P L m L r ( ψ r d K i s q K ) .

2.9. Постоянная времени ротора

T_r=L_r/R_r.

2.10. Угловая скорость ротора

ω = ω r = ω 2 = i s q K ⋅ L m ψ s d K T r .

Полученные выше в операциях 2.1-2.10 значения величин позволяют осуществить регулирование отдельных величин в зависимости от конкретной функциональной схемы электропривода с векторным управлением. Так усиленное значение разности между заданным извне заданием угловой скорости ротора и вычисленным значением угловой скорости ротора (п.2.10) может служить сигналом изменения величины моментообразующей составляющей тока статора i_sqk (п.2.7). При этом усиление разности между заданием модуля магнитного потокосцепления ротора и его вычисленным значением ψ_rmK (п.2.4) может служить сигналом управления амплитудой напряжения инвертора, обеспечивающим стабилизацию магнитного потокосцепления ротора. Поданный извне сигнал задания угловой скорости ротора может использоваться в качестве сигнала задания частоты напряжения на выходе инвертора, подаваемого на статор двигателя. Таким образом, указанные для предлагаемого способа операции обработки сигналов (пп.2.1-2.10) позволяют построить различные системы векторного управления электроприводом, что обеспечивает учет системой управления важнейших для векторного управления конструктивных особенностей трехфазной машины, создающих несинусоидальность распределения магнитной индукции вдоль воздушного зазора машины.

Применение предлагаемого способа векторного управления скоростью трехфазной машины. В качестве примера приведено описание системы асинхронного электропривода с векторным управлением без датчика скорости. Функциональная схема электропривода с использованием предлагаемого способа управления показана на фиг.3. Структура привода является одной из самых простых и достаточно эффективной для применения предлагаемого способа векторного управления. Асинхронный двигатель 1 подключен к инвертору напряжения 2. Сигнал задания величины модуля магнитного потокосцепления 3 ротора и вычисленное в системе управления приводом значение модуля магнитного потокосцепления ротора 4 подключены к входам узла сравнения 5. Выход узла сравнения 5 соединен с блоком 6. Сигнал 7 с выхода блока 6 соединен с входом блока 8. Сформированный сигнал задания скорости вращения 9 соединен с входом блока 8 и выходом задатчика интенсивности изменения скорости вращения (задатчика ускорения двигателя) 10, вход последнего является внешним входом задания скорости вращения 11. Сигнал 12 соединен с выходом блока 8 и входом ограничителя уровня 13, выход которого служит сигналом 14 для управления величиной напряжения, создаваемого инвертором 2 на статоре двигателя 1. Сформированный сигнал задания скорости вращения 9 связан с входом формирователя интенсивности 15. С выхода формирователя 15 сигнал задания частоты 16 соединен с выходом управления частотой инвертора 2. Трехфазный датчик 17 имеет три ввода от трех фазных напряжений статора и три вывода, которые соединены с тремя входами преобразователя 18. Сигналы 19 с двух выходов преобразователя 18 соединены с двумя входами вычислителя 20. Сигналы двух проекции магнитного потока ротора 21 с двух выходов вычислителя 20 соединены с двумя входами вычислителя 22 модуля обобщенного вектора магнитного потокосцепления ротора. С выхода блока 22 сигнал 4 модуля обобщенного вектора магнитного потокосцепления ротора соединен с инверсным входом узла сравнения 5. Два других входа вычислителя проекций 20 соединены с сигналами двух проекции обобщенного вектора тока статора 23, которые связаны с двумя выходами преобразователя координат 24. Три входа преобразователя координат 24 соединены с тремя выходами датчика 26 фазных токов статора.

Работа системы управления электропривода происходит следующим образом. Асинхронный двигатель 1 (фиг.3) получает питание от инвертора напряжения 2, работающего с широтно-импульсной модуляцией с регулированием амплитуды и частоты напряжений (u_sA u_sB u_sC) на статоре двигателя 1. Привод построен со стабилизацией магнитного потокосцепления ротора (ψ_rmK) и с управлением скоростью вращения ω двигателя. Сигнал здания величины магнитного потокосцепления 3 ( ψ r m z ) ротора и вычисленное в системе управления приводом значение магнитного потокосцепления ротора 4 (ψ_rmK) сравниваются между собой в узле сравнения 5. Сигнал разности магнитных потокосцеплений Δ ψ r m = ( ψ r m z − ψ r m K ) с узла 5 поступает в блок 6, где он (Δψ_rm) формируется по интенсивности изменения и ограничивается по уровню. Сформированный сигнал 7 перемножается в блоке 8 с сигналом скорости вращения (ω^z) 9, поступающим через задатчик интенсивности изменения скорости вращения (задатчик ускорения) 10 со входа задания скорости вращения ( ω 0 z ) 11. С выхода блока перемножения 8 сигнал 12 проходит через ограничитель уровня 13 и служит сигналом (U_sm) 14 для управления величиной напряжения, создаваемого инвертором 2 на статоре двигателя 1. Сигнал скорости вращения (ω^z) 9 поступает через формирователь интенсивности его изменения 15 как сигнал задания частоты (ω₀) 16 на выходе инвертора 2. Сигнал (ω₀) 16 с точностью до скольжения задает скорость вращения (ω) двигателя 1. Трехфазный датчик 17 созданных на двигателе 1 фазных напряжений статора (u_sA u_sB u_sC) подает эти напряжения на преобразователь 18, в котором из трехфазной системы векторов формируются ортогональные проекции в двухфазной ортогональной системе векторов (u_αK, u_βK) 19 обобщенного вектора напряжений статора. Ортогональные проекции обобщенного вектора напряжений статора (u_αK, u_βK) 19 поступают в вычислитель 20 проекций магнитного потокосцепления ротора (ψ_rdK ψ_rqK) 21 и затем в вычислитель 22 модуля обобщенного вектора магнитного потокосцепления ротора (ψ_rmK). По проекциям магнитного потокосцепления ротора (ψ_rdK ψ_rqK) в блоке 22 вычисляется модуль (ψ_rmK) 4 магнитного потокосцепления ротора. В вычислителе проекций (ψ_rdK ψ_rqK) 20 используются ортогональные двухфазные проекции (i_αK, i_βK) 23 обобщенного вектора тока статора, создаваемые в преобразователе трехфазной системы координат в двухфазную ортогональную систему координат 24 по сигналам от датчиков 26 трех фазных токов (i_sA i_sB i_sC) статора. Предлагаемый способ управления скоростью вращения трехфазной машины используется в рассматриваемом приводе в преобразователе координат 18 для уточненного преобразования системы трех векторов фазных напряжений статора в двухфазную ортогональную систему проекции 19 обобщенного вектора напряжений стато