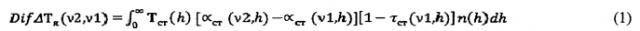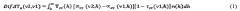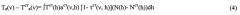Дифференциальный способ определения вертикального профиля концентрации газов в атмосфере

Дифференциальный способ определения вертикального профиля концентрации газов в атмосфере

Иллюстрации

Показать все

Реферат

Изобретение относится к дистанционному измерению высотного распределения концентрации газов в атмосфере по собственному тепловому излучению в окрестности линии поглощения измеряемого газа. Например, измерению вертикального профиля водяного пара по радиометрическим измерениям, как с поверхности земли, так и со спутника в полосе поглощения водяного пара.

Известен способ определения профиля концентрации озона на основе измерения формы линии поглощения озона при регистрации со спутника излучения Солнца во время заката или восхода [1].

Недостатком данного способа является невысокая точность измерений из-за предположения о модели слоисто однородного распределения концентрации газа, что выполняется не всегда. Другим недостатком является усреднение по большой горизонтальной области

Другим способом является регистрации микроволнового излучения в линии поглощения некоторого газа и восстановление вертикального профиля концентрации данного газа по различию яркостной температуры на различных частотах в окрестности линии поглощения [2].

Недостатком данного способа является невысокая точность измерений из-за сильного изменения (на 3-4 порядка) измеряемой величины с высотой, что приводит к маскировке даже сильных изменений концентрации на больших высотах на фоне небольших относительных изменений концентрации на малых высотах.

Наиболее близким аналогом является радиометрический спектральный способ измерения влажности в стратосфере [3]. При этом на земле или на спутнике устанавливается радиометр, работающий на различных частотах в окрестности линии поглощения измеряемого газа. Измеряется радиояркостная температура, которая чувствительна к профилю измеряемого газа, проводится ее сравнение с расчетными значениями, полученными на основе априорных или стандартных данных о вертикальных профилях температуры, атмосферного давления и концентрации измеряемого газа, а, исходя из различий этих величин, вычисляется искомый профиль измеряемого газа.

Однако данный метод имеет невысокую точность, поскольку не позволяет учесть высоко изменчивый вклад облаков и осадков на результаты измерений.

Технический результат предложенного способа заключается в повышении точности измерений и резком снижении влияния других газов, облаков и осадков за счет того, что для получения концентрации газа на заданной высоте радиометрические измерения проводят на двух парах частот, расположенных на различных склонах линии поглощения измеряемого газа, которая соответствует заданной высоте, и используют разность или линейную комбинацию дифференциальных радиометрических сигналов на этих частотах.

Достоинством предлагаемого способа является повышение точности за счет дифференциального характера измерений, при котором не требуется абсолютная калибровка радиометра и вычитаются вклады всех факторов (сторонних газов, облаков, осадков, подстилающей поверхности), у которых спектральная зависимость поглощения в диапазоне измерений имеет нерезонансный характер.

На фиг.1 представлена схема радиометрических измерений с поверхности земли при наблюдении в зенит. 1 - радиометр, проводящий измерения на заданном наборе частот, 2 - облака, 3 - атмосфера, 4 - излучение фона.

На фиг.2 показаны радиометрические измерения в борта летательного аппарата - 1 или спутника под некоторым углом к вертикали. При этом суммируются сигналы, сформированные атмосферой 2, облаками 3 и подстилающей поверхностью 4.

На фиг.3 показан качественный вид частотной зависимости собственного излучения Т_я(ν), сформированного нижним, средним и верхним слоем атмосферы, кривые 1, 2, и 3, соответственно, частотная зависимость собственного излучения облаков и осадков - кривая 4 и спектральная зависимость излучения фона или подстилающей поверхности 5. Графики выполнены в полулогарифмическом масштабе. Чем выше расположен слой измеряемого газа, тем уже его полоса поглощения. При дифференциальных радиометрических измерениях на частотах ν1, ν2 условно можно считать, что полный сигнал радиометра ΔТ_я(ν1,ν2,) складывается из дифференциальных сигналов ΔТ_я,i(,), отмеченных на оси абсцисс для всех пяти кривых. Аналогично формируется сигнал и на частотах ν3, ν4, расположенных на противоположном склоне линии поглощения. На этих частотах дифференциальные сигналы от нижнего слоя атмосферы ΔТ_я,1(ν3,ν4,), облаков ΔТ_я,4(ν3,ν4) и фона (подстилающей поверхности) ΔТ_я,5(ν3,ν4,) остаются почти такими же, как на частотах ν1, ν2, а сигналы от нужного среднего слоя ΔТ_я,2(ν3,ν4) и верхнего слоя ΔТ_я,3(ν3,ν4) изменяют знак.

На фиг.4 представлены результаты расчетов по формуле (1) вклада различных слоев атмосферы и облаков в радиометрический сигнал, проведенных в окрестности полосы поглощения водяного пара 22.235 ГГц. а) - дифференциальный сигнал на частотах ν1=22.221 ГГц, ν2=22.23 ГГц, расположенных на низкочастотном склоне линии поглощения, б) такой же сигнал на частотах ν3=22.24 и ν4=22.249, расположенных на высокочастотном склоне, в) разность дифференциальных сигналов позволяет вычесть вклады нижнего слоя, облаков, подстилающей поверхности и удвоить сигнал от интересующего нас среднего слоя на высоте 40 км.

На фиг.5 показана высотная избирательность ядер интегрального уравнения к водяному пару в окрестности линии 22 ГГц. Кривые 1-5 используют набор частот, представленных в таблице 1.

Рассмотрим физический принцип предложенного способа на основе фиг.3 и фиг.4. Если условно разбить всю атмосферу на три слоя плюс облака и осадки, плюс фон или подстилающая поверхность, то можно считать, что общий дифференциальный радиометрический сигнал на частотах ν1, ν2 по траектории распространения излучения складывается из дифференциальных сигналов ΔТ_я,i(ν1,ν2,), отмеченных на фиг.3 по оси абсцисс для всех пяти кривых. Из графиков видно, что для верхнего слоя, кривая 3, разница ΔТ_я,3(ν1,ν2,), мала, следовательно, данный слой в общий сигнал дает малый вклад. Наибольшее различие ΔТ_я,2(ν1,ν2,), возникает для нужного среднего слоя (кривая 2). Дополнительный вклад в общий сигнал дают облака и осадки ΔТ_я,4(ν1,ν2,), нижний слой атмосферы ΔТ_я,1(ν1,ν2,), и фон или подстилающая поверхность ΔТ_я,5(ν1,ν2,). Учитывая логарифмический характер графика, эти вклады могут быть сравнимыми с сигналом ΔТ_я,2(ν1,ν2,), что маскирует вклад этого слоя.

На фиг.4а рассчитаны вклады в дифференциальный сигнал в окрестности полосы поглощения водяного пара 22.235 ГГц, от различных слоев атмосферы к которым добавлен вклад облаков на высоте 3-5 км. Вклад фона или подстилающей поверхности в графике не показан, т.к. он имеет некоторую постоянную величину, не зависящую от высоты.

При выборе двух частот ν3, ν4 на другом склоне линии поглощения, фиг.3, вклад слоя 2 ΔТ_я,2(ν3,ν4,), меняет знак на противоположенный, поскольку изменяется знак производной, а вклады нижнего слоя 1, облаков 4 и подстилающей поверхности 5 знак не изменяют, фиг.4б. Поэтому разность дифференциальных сигналов на различных склонах линии поглощения позволяет вычесть все маскирующие факторы: нижний слой, облака и осадки, а также подстилающую поверхность, при этом удвоить вклад интересующего нас среднего слоя 2, фиг.4в. В некоторых случаях целесообразно проводить вычитание дифференциальных сигналов с некоторым коэффициентом С, который учитывает спектральную нелинейность того фактора, который требуется максимально снизить. ΔТ_я,(ν1,ν2,)-С ΔТ_я,(ν3,ν4,).

Пример определения профиля концентрации газов до высоты 80 км с помощью радиометра, установленного на поверхности земли, фиг.1, приведен для водяного пара в полосе поглощения 22,235 ГГц. Отклонение измеряемого дифференциального сигнала радиометра ΔТ_я(ν2,ν1) от его расчетного значения ΔТ_{я ст}(ν2,ν1), ожидаемого для стандартной атмосферы, обозначим DifΔТ_я(ν2,ν1). Эту величину можно выразить соотношением:

где n(h)=[N(h)-N_ст(h)]/N_ст(h) - относительное отклонение концентрации измеряемого газа N(h) от стандартного профиля N_ст(h), величины α_ст(ν2,h)=α(ν2,h)N_ст(h) и α_ст(ν1,h)=а(ν1,h)N_ст(h) - зависимости линейного коэффициента поглощения газа для стандартного профиля концентрации водяного пара на частотах ν2 и ν1, соответственно. Весовой функцией или ядром интегрального уравнения (1) является величина W(ν1,ν2,h)=T_ст(h)[α_ст(ν2,h)-α_ст(ν1,h)][1-τ_ст(ν1,h)].

На фиг.4а представлен расчет зависимости дифференциального сигнала от высоты слоя (ядро интегрального уравнения) на низкочастотном склоне линии поглощения при использовании частот ν1=22.221 ГГц, ν2=22.23 ГГц. На высотах 1-10 км к вкладу водяного пара добавляется вклад облака, который находится на высоте 3-4 км. Производная (наклон кривых на фиг.3), d(Т_я)/dH, на этом склоне линии поглощения положительна, поэтому дифференциальный сигнал на всех высотах имеет положительные значения. При симметричном выборе частот ν3=22.24 и ν4=22.249 на высокочастотном склоне линии поглощения, фиг.3, производная d(Т_я)/dH изменяет знак для слоя 2 и слоя 3, а остальные слои, включая нижний слой атмосферы, слой облаков, знак не изменяют. В результате получаем зависимость дифференциального сигнала от высоты, фиг.4б, в которой вклад слоя 2 изменил знак, а вклады облаков и нижнего слоя почти остались прежними. Линейная комбинация дифференциальных сигналов, состоящая из ΔТ_я,(ν1,ν2,)-0.95 ΔТ_я,(ν3,ν4,) дают результирующее ядро, представленное на фигуре 4в. Как видно, это ядро имеет четко выраженную максимальную чувствительность на высоте 41 километра и практически не чувствует вклад нижних слоев атмосферы и облаков. Аналогичным образом происходит вычитание влияния любых других факторов дающих вклад в дифференциальный радиометрический сигнал, если на используемом интервале частот (ν1…ν4) спектральная характеристика этих механизмов ослабления не имеет резонансную форму, а плавно изменяется на используемом интервале. В частности, вычитаются собственное излучение других атмосферных газов, излучение осадков, фона или подстилающей поверхности при зондировании по схеме, представленной на фиг.2

Для получения профиля концентрации искомого газа по высоте следует использовать весь набор частот, представленный в таблице. При этом каждая комбинация частот, в соответствии с фиг.5, полученной для водяного пара, выделяет свою высоту. Например, если реальный профиль водяного пара близок к стандартному и только на высотах 55-68 км имеет повышенную на 30% концентрацию относительно стандартного профиля, то лишь 4-й набор частот из таблицы даст сигнал положительный по знаку, который составит величину на 30% больше, чем у стандартного профиля. Остальные наборы частот на это изменение не отреагируют, т.к. их ядра к этому диапазону частот не чувствительны. Поэтому, остальные наборы частот дадут нулевое отклонение от стандарта, что будет свидетельствовать о стандартном профиле на остальной части атмосферы. По величине изменения концентрации относительно стандартной атмосферы нетрудно вычислить и профиль абсолютной концентрации водяного пара на различных высотах.

Достоинством предложенного метода является дифференциальный подход к решению обратной задачи, позволяющий снизить требования к точности абсолютных измерений, отказаться от абсолютной калибровки приемников, повысить чувствительность приборов к измеряемым величинам.

Изобретательский уровень предлагаемого технического решения подтверждается отличительной частью формулы изобретения.

Литература

1. Krueger A.J., Guenther В., Fleig A.J. et al. Satellite ozone measurements // Phil. Trans. Roy. Soc. London. - 1980. - V.A296. - №1. - P.191-204.

2. Горелик А.Г., Князев Л.В., Прозоровский А.Ю. Предельная чувствительность спектрометрических измерений влажности в стратосфере и мезосфере в линии поглощения водяного пара λ=1.35 см. Труды Всесоюзного симпозиума по радиофизическим методам исследования атмосферы. Л-д. Гидрометеоиздат. 1977, с.223-228.

3. Haefele A., Kampfer N. Tropospheric Water Vapor Profiles Retrieved from Pressure-Broadened Emission Spectra at 22 GHz. J. // Atmospheric and Oceanic Technology. 2010. V.27, p.167-172.

Приложение 1

К изобретению: Дифференциальный способ определения вертикального профиля концентрации газов в атмосфере

Интегральные уравнения при измерениях на отдельных частотах

Рассмотрим радиотепловые измерения, проводимые с поверхности земли в зенит. Яркостная температура, регистрируемая в узкой полосе приема с центром на частоте ν, можно выразить соотношением:

где первое слагаемое описывает вклад внеатмосферного излучения, а второй - вклад атмосферы, Т_ф - фоновая температура за счет внеатмосферных источников, T(h) - вертикальный профиль термодинамической температуры, α(ν,h) и γ(ν, h) - профили линейного коэффициента поглощения и ослабления на заданной частоте, соответственно, экспоненциальный сомножитель во втором слагаемом описывает ослабления сигнала, сформированного слоем (h,h+dh),.

На первом этапе рассмотрим собственное излучение атмосферы, предполагая отсутствие облаков и осадков. Для многих парниковых газов рассеянием на молекулах воздуха в полосах поглощения искомого газа можно пренебречь, тогда подавляющий вклад в ослабление дает поглощение, и в (1) можно провести замену γ(ν,h)≈α(ν,h). Если плотность атмосферы невелика,

то целесообразно рассмотреть линейное приближение ехр(-τ₀)≈1-τ₀. Поскольку линейный коэффициент поглощения α(ν,h) пропорционален концентрации газа N(h), то его удобно представить в виде произведения α(ν,h)=a(ν,h)N(h), где величина a(ν,h) уже не зависит от концентрации газа. В этих предположениях соотношение (1) приобретает вид:

где τ₀(ν) - полное поглощение атмосферы на заданной частоте, a τ(ν,h) - поглощение в слое (0-h).

При решении обратных задач вида (2) широко используются методы статистической регуляризации, которые опираются на использование априорной информации о стандартных профилях температуры T^ст(h), давления P^ст(h) и концентрации измеряемого газа N^ст(h). В этом случае рассчитывается яркостная температура для стандартной атмосферы

а затем используется отклонение измеряемой яркостной температуры от ее расчетного значения. В первом приближении, если расчетные профили учитывают данные наземных значений давления, температуры и влажности, вполне можно в уравнениях (2) и (3) положить, что T(h)=T^ст(h), а(ν,h)=a^ст(ν,h)), τ(ν, h)=τ^ст(ν,h). В этих предположениях мы получим:

Полученное уравнение является интегральным уравнением Фредгольма 1 рода, в котором неизвестной величиной является отклонение концентрации искомого газа от стандартного профиля ΔN(h)=N(h)-N^ст(h), а зависимость W(h)=T^ст(h)a^ст(ν,h)[1-τ^ст(ν,h)] является весовой функцией или ядром интегрального уравнения. Качество восстановления определяется узостью ядра интегрального уравнения по высоте: чем уже максимум весовой функции (ядра), тем надежней регистрируется концентрация искомого газа в области максимума. На рис.1 слева представлены нормированные по максимуму ядра интегрального уравнения (4), в котором неизвестной восстанавливаемой величиной является отклонение концентрации искомого газа от стандартного профиля ΔN(h)=N(h)-N^ст(h). Для расчетов коэффициентов поглощения мы использовали формулы, полученные Д. Крумом (Krum, 1965) и С.А. Жевакиным, А.П. Наумовым (Жевакин, Наумов, 1964). Для высот свыше 60 км в формулах учитывалось доплеровское уширение линии, исходя их соотношения, приведенного в работе {Krum, 1965). На первый взгляд может показаться, что ядра имеют хорошую избирательность по высоте и могут вполне использоваться для решения обратной задачи. Но это не так. Недостаток такого подхода заключается в том, что концентрация искомого газа по трассе измерений обычно изменяется на 3-6 порядков. Поэтому видимое снижение весовой функции на малой высоте ничего не говорит о качестве восстановления, поскольку вклад этой функции должен быть умножен на величину порядка 10³-10⁶ за счет высокой концентрации газа на нижних высотах.

Чтобы исключить фактор сильного изменения концентрации с высотой следует искомой величиной выбирать относительное отклонение концентрации измеряемого газа от стандартного профиля, а именно, n(h)=[N(h)-N_ст(h)]/N_ст(h). Данная величина вдоль трассы измерений варьируется в едином масштабе сравнимом с единицей, поэтому интегральные ядра в предложенном способе будут наглядно демонстрировать чувствительность метода к изменениям концентрации искомого газа в атмосфере.

Из уравнения (4) нетрудно получить интегральное выражение для относительного отклонения концентрации измеряемого газа от стандартного профиля:

Здесь α_ст(h,ν)=a(h,ν)N_ст(h) - линейный коэффициент поглощения для стандартной атмосферы, a n(h)=[N(h)-N_ст(h)]/N_ст(h) - относительное отклонение измеряемой концентрации от стандартной. На рисунке 2 справа показано, что при использовании уравнения (5) и поиске относительного отклонения концентрации от стандартной атмосферы избирательность ядер пропадает. На всех частотах измерений вклад нижних слоев играет основную роль и многократно перекрывает вклады верхних. Это означает, что использовать уравнения (3) или (5) для восстановления профиля газа невозможно.

Дифференциальный радиометрический метод измерения на двух частотах

Качество решения обратной задачи кардинально улучшается при использовании дифференциального метода, в котором измеряется разность сигналов на двух близких длинах волн. Рассмотрим ситуацию более подробно. Пусть радиометр проводит измерения на заданной паре частот ν1 и ν2, с некоторой шириной полосы, которая существенно меньше разности частот ν2-ν1. При этом на приемнике регистрируется дифференциальный сигнал ΔТ_я(ν1,ν2)=Т_я(ν2)-Т_я(ν1). В тех же предположениях об отсутствии облаков и осадков и пренебрежения рассеянием на молекулах воздуха получим:

где Δτ₀(ν2,ν1)]=τ₀(ν2)-τ₀(ν1) - разность общего поглощения атмосферы на заданной паре частот, зависимость a(r,ν) связана с линейным коэффициентом поглощения α(r,ν) соотношением α(r,ν)=a(r,ν)N(r). Приведенное уравнение, вообще говоря, нелинейное по отношению к N(r), поскольку τ(ν,h) зависит от N(r). Рассмотрим возможность его линеаризации. Подынтегральное выражение удобно несколько видоизменить, разбив на три слагаемых:

Рассмотрим масштаб каждого слагаемого для стандартной атмосферы. На рис.2 приведены типичные высотные зависимости для каждого из трех слагаемых и результирующее ядро в целом.

Из рис.2 следует, что второе слагаемое в подынтегральном уравнении много меньше, чем первое и третье, поэтому им можно пренебречь и уравнение (6) можно линеаризовать по измеряемой величине N(h):

В данном соотношении величина [1-τ(ν,h)] практически постоянна и почти не зависит от N(h). Если принять уравнение Фредгольма в форме (8) за основу и проводить восстановление концентрации искомого газа N(r), то, на первый взгляд, мы имеем прекрасные ядра с высокой избирательностью. На рис.3 слева показана типичная форма ядер интегрального уравнения (8), рассчитанная для полосы водяного пара 22,235 ГГц при дифференциальных измерениях на двух частотах ν1=22,221 ГГц и ν2=22,23 ГГц. Однако, как и в первом примере, в уравнении (8) имеется скрытый подвох. Подвох заключается в том, что ядро уравнения (8) говорит о том вкладе, который дают в дифференциальный сигнал одинаковое число молекул, находящихся на разных высотах. Да, 1000 молекул на высоте 40 км дают больший вклад в сигнал, чем 1000 молекул на высоте 1 км. Но масштабы изменений на высоте 1 км в 10000 выше, чем на 40 км, поэтому может оказаться, что 1% изменение концентрации газа у земли перекроет 100% изменение концентрации газа на 40 км. В этом случае задачу решить не удастся, какие бы методы регуляризации не применялись. Для корректной оценки точности решения обратной задачи следует обратиться к относительному отклонению измеренных величин от их же значений, полученных для стандартной атмосферы. Найдем вид интегральных уравнений для относительного изменения концентрации водяного пара.

По аналогии с предыдущим примером введем расчетное значение ΔТ_{я ст}(ν2,ν1), ожидаемое для стандартной атмосферы, и вычислим отклонение измеряемой величины ΔТ_я(ν2,ν1) от стандартной. Эту величину обозначим DifΔТ_я(ν2,ν1)

Учитывая, что фоновое излучение вычитается, и используя те же предположения, что T(h)=T^ст(h), α(ν,h)=a^cт(ν,h)), t(ν,h)=τ^ст(ν,h), получим:

где n(h)=[N(h)-N_ст(h)]/N_ст(h) - относительное отклонение концентрации измеряемого газа от стандартного профиля, величины α_ст(ν2,h)=a(ν2,h)N_ст(h) и α_ст(ν1,h)=а(ν1,h)N_ст(h) - зависимости линейного коэффициента поглощения газа для стандартного профиля концентрации водяного пара на частотах ν2 и ν1, соответственно. Весовой функцией или ядром интегрального уравнения (1) является величина W(ν1,ν2,h)=T_ст(h)[α_ст(ν2,h)-α_ст(ν1,h)][1-τ_ст(ν1,h)].

Теперь мы можем оценить истинную избирательность дифференциальных измерений, поскольку относительное изменение концентрации, функция n(r), имеет одинаковый масштаб изменений на всех высотах. На рисунке 3 справа представлена (нормированная на максимум) форма ядра интегрального уравнения (9) для тех же частот ν1=22,221 ГГц и ν2=22,23 ГГц, что и ядро, представленное слева на рис.3. Из рисунка видно, что наряду с максимумом на 40 км ядро имеет высокую чувствительность и к слою на высотах 0-6 км. Отметим, что истинное положение максимума на рис.3 справа смещено к меньшим высотам, чем на рис 3 слева. Это связано с тем, что ядро уравнения (9) учитывает падение концентрации водяного пара с высотой.

Особенностью ядер интегрального уравнения (9) является их знакопеременный характер, который можно эффективно использовать при решении обратной задачи. Далее мы рассмотрим возможности улучшения избирательности ядер и снижения вкладов нижних слоев с очень высокими концентрациями измеряемого газа. Предложенный ниже разностно-дифференциальный метод позволяет не только уменьшить вклад нижних слоев, но и практически убрать вклады облаков и осадков, а также избавиться от влияния других атмосферных газов.

Разностно-дифференциальный метод, использующий разность дифференциальных радиометрических сигналов на двух склонах линии поглощения

При качественном рассмотрении вопроса о свойствах ядра интегрального уравнения (9) в первую очередь следует иметь в виду, что в выражении для ядра:

основная изменчивость с высотой формируется разностью линейных поглощений [α_ст(ν2,h)-(α_ст(ν1,h)], в то время как температура T_ст(n) и величина [1-τ_ст(ν1,h)] изменяются по высоте относительно слабо. По этой причине анализ свойств ядра следует рассматривать как анализ свойств величины [α_ст(ν2,h)-α_ст(ν1,h)].

При расчете ядер интегральных уравнений в дифференциальном методе перед нами встал следующий вопрос. А на каком склоне линии поглощения лучше выбирать пары частот? Ведь, с первого взгляда, форма линии поглощения на больших высотах почти симметрична, и избирательность должна быть почти одинакова при выборе пары частот на обоих склонах линии поглощения. В действительности, линия поглощения не симметрична, что обусловлено влиянием других линий водяного пара, вкладом облаков, осадков и других газов атмосферы. Это свойство можно использовать для существенного снижения влияния факторов, вызывающих асимметрию.

На рис.4 рассчитаны кривые для дифференциальной яркостной температуры стандартной атмосферы в окрестности полосы поглощения водяного пара 22.235 ГГц, и показан пример, как использование линейной комбинации двух пар частот на разных склонах линии поглощения позволяет резко снизить влияние нижних слоев на ядра, получаемые для верхних слоев атмосферы. Первая кривая - ядро интегрального уравнения (9) или дифференциальная яркостная температура для стандартной атмосферы T_ст(h)[α_ст(ν2,h)-α_ст(ν1,h)][1-τ_ст(ν1,h)] на частотах ν1=22.221 ГГц, ν2=22.23 ГГц. На данной кривой виден значительный вклад нижних слоев в общую площадь под кривой. Кривая 2 - дифференциальная яркостная температура T_ст(h)[α_ст(ν4,h)-α_ст(ν3,h)][1-τ_ст(ν3,h)] на другом склоне линии при ν3=22.24 и ν4=22.249. Вторая пара частот симметрична относительно центра линии поглощения. Вклад верхних слоев для этого склона линии имеет тот же знак, что и на первом ядре, в то время как полезный сигнал на 40 км имеет противоположный по сравнению с первым ядром знак. (Это связано с изменением знака производной при переходе на другой склон линии поглощения). Кривая 3 - разность первого и второго графика удваивает вклад на требуемом 40 км участке высот и взаимно вычитает вклады нижнего слоя газа. Если на первом и втором графиках вклад нижних высот в сигнал (площадь под кривой на участке высот 0-8 км) превышает вклад требуемого слоя 35-45 км почти в 1,5 раза, то на третьем графике удается выделить вклад интересующего нас слоя почти в чистом виде.

Высокая избирательность ядер по высотам не единственное достоинство предлагаемого метода. Линейная комбинация дифференциальной яркостной температуры на разных склонах линии позволяет вычесть вклады облаков и осадков, а также влияние других газов атмосферы. Рассмотрим этот механизм более подробно.

Как мы уже отмечали, основная изменчивость ядра радиометрического уравнения с высотой обусловлена разностью линейного поглощения на двух частотах. На рис.5 показан качественный вид частотной зависимости поглощения излучения водяным паром α_ст(r,ν) для верхних, средних и нижних слоев атмосферы, кривые 1, 2, и 3, соответственно. Чем выше рассматриваемый слой газа, тем уже ширина спектральной линии поглощения. Кривая 4 демонстрирует частотную зависимость поглощения для облаков и осадков. Графики выполнены в полулогарифмическом масштабе. Условно можно считать, что общее дифференциальная яркостная температура всей атмосферы по траектории распространения складывается из разности коэффициентов поглощения α_ст(h,ν2)-α_ст(h,ν1) всех четыре кривых. Из графика видно, что наибольшая разница коэффициентов поглощения на частотах ν2 и ν1, (показанных пунктиром слева от максимума) возникает для слоя 2, который мы и хотим выделить. Вклады же верхнего слоя атмосферы (кривая 1) и нижнего слоя (кривая 3) имеют небольшую разницу на этих частотах, хотя нижний слой 3, если учесть логарифмический масштаб графика, может создать определенную разность поглощений. Определенную разницу на ν2 и ν1 также имеют облака, вклад которых показан кривой 4.

Перейдем теперь к частотам ν3 и ν4, расположенным симметрично относительно центра на правом склоне линии поглощения. Заметим, что если из α_ст(Н,ν4) вычитать α_ст(Н,ν3), то данная разница на нужном слое 2, поменяет знак, в то время как эта разница для нижнего слоя 3 и осадков 4 останется положительной (смотри рис.4). В результате, вычитая дифференциальные сигналы на разных склонах линии поглощения, мы удвоим полезный сигнал, и вычтем сигналы от нижнего слоя, облаков, осадков и других газов атмосферы.

Если бы на интервале частот ν1 и ν4 вклад нижнего слоя 3 и осадков 4 имел бы постоянное значение или линейную зависимость от частоты, то при таком вычитании их влияние на результирующее ядро полностью бы компенсировалось. В действительности имеется определенная нелинейность у кривых 3 и 4, поэтому компенсация при простом вычитании дифференциальных сигналов будет не полной. В зависимости от поставленной задачи, можно учесть наиболее нежелательную нелинейность за счет вычитания дифференциальных сигналов с некоторым весовым коэффициентом С, а именно взять линейную комбинацию DifΔТ_я(ν2,ν1)-C DifΔT_я(ν4,ν3), которая имеет ядро W_difdif(ν1,ν2,ν3,ν4)=(T_ст(h)[α_ст(ν2,h)-α_ст(ν1,h)][1-τ_ст(ν1,h)]-CT_ст(h)[α_ст(ν4,h)-α_ст(ν3,h)][1-τ_ст(ν3,h)]. При правильном подборе коэффициента С вклад нежелательного фактора можно обнулить, правда при этом вклад другого нелинейного фактора может слегка увеличиться. Учитывая, что на высотах 30-80 км кривая поглощения водяного пара имеет ярко выраженный резонансный характер, а все прочие факторы, влияющие на ослабление, изменяются плавно, предложенная методика вычитания дифференциальных сигналов на двух склонах линии поглощения является весьма эффективным инструментом подавления нежелательных вкладов. На рис.4 показаны результаты подавления вклада нижних слоев атмосферы, но столь же эффективно будут вычитаться и вклады облаков, осадков, других атмосферных газов, у которых в области измерений нет резонансных линий.

В результате процедуры подбора частот для задачи восстановления профиля водяного пара при радиометрических измерениях в окрестности линии поглощения 22,235 ГГц были получены ядра интегрального уравнения (9), представленные на рисунках 6 и 7. Ядра представляют собой ненормированные и нормированные на максимальное значение зависимости W(h,ν1,ν2)=T_ст(h)[α_ст(ν2,h)-α_ст(ν1,h)][1-τ_ст(ν1,h)], которые описывают вклад различных высот в измеряемую величину n(Н) (относительное в % отклонение концентрации водяного пара от стандартной атмосферы) при радиометрических измерений в надир.. Значения частот для каждой кривой приведены в таблице. Весовые функции 4-8 используют линейную комбинацию двух ядер на различных склонах линии поглощения измеряемого газа, поэтому для этих кривых даны 4 частоты, - по две на каждом склоне линии поглощения.

Отметим, что форма линии поглощения водяного пара на частоте 22,235 ГГц имеет ту особенность, что не удается получить ядра, которые имели бы четкий максимум в интервале высот 8-25 км. Удается лишь получить хорошие ядра для слоя 0-8 км с полушириной около 4 км, и неплохие ядра для высот 30-85 км с полушириной около 15 км. По этой причине мы представили отдельно на рис.6 три ядра для нижнего слоя, а на рисунке 7 ядра для верхних слоев атмосферы.. В таблице 1 приведены значения частот, которые соответствуют каждой кривой на рис.6 и рис.7, а для кривых 4-11 приведены значения частот на двух склонах линии поглощения. В последней колонке таблицы даны высотный диапазон усреднения для каждой весовой функции и высота, на которой достигается максимум весовой функции. Расчеты выполнены для распространения излучения по вертикали, в зенит. При наклонном распространении качественный характер всех зависимостей не изменится.

Оценка возможности измерения профиля водяного пара с поверхности земли в полосе 22 ГГц

Для оценки возможности проведения радиометрических измерений концентрации водяного пара до высоты 80 км с поверхности земли требуется оценить ширину полосы приема, которая является допустимой для каждой заданной высоты зондирования. Из рис.5 следует, что полоса приема радиометра в дифференциальном методе не может быть слишком большой, поскольку при этом будет размываться и теряется избирательность дифференциальных измерений. С другой стороны полоса приема не должна быть слишком узкой, поскольку в этом случае снижается чувствительность измерений.

С учетом полосы измерений приемника интегральное уравнение примет следующий вид:

где, по сравнению с уравнением (9), проводится интегрирование сигнала в полосе приема Δν.

Исходя из формы линии поглощения и проведенных оценок уравнения (10), можно принять, что оптимальная ширина приема составляет примерно одну третью часть от разницы частот в дифференциальных измерениях. Чем ниже высота зондирования, тем шире полоса приема, тем выше ожидаемая разница яркостных температур ΔТ_я(ν2,ν1), выше уровень сигнала и легче проводить дифференциальные измерения. В качестве примера проведем оценку возможности проведения радиометрических измерений для верхних слоев, например для высоты 54 км, (ядро 8 на рис.7). Из формы ядра следует, что ожидаемый уровень сигнала (интеграл под кривой) будет составлять ΔТ_я(ν2,ν1)=2*10^-2 К. Оптимальная ширина полосы приемника на данной высоте составит Δν=0,3*10⁶ Гц. При оценке шумовой температуры всего радиометра в Т_ш=10³ К, накопление сигнала Δτ должно составить: Δτ=(1/Δν)(Т_ш/ΔТ_я)²=7,5*10³ с, то есть около 2 часов.

Очевидно, что для более низких слоев время накопления сигнала можно уменьшить. Аналогичная оценка, проведенная для высоты измерений 5 км, дает полосу Δν=1,5*10⁸ Гц, уровень дифференциального сигнала ΔТ_я(ν2,ν1)=1 К, что при той же шумовой температуре приемника Т_ш=10³ К, и требовании к отношению сигнал/шум=5, потребует накопления сигнала в течении 1 с.

Для получения данных о профиле водяного пара на высотах свыше 50 км требуется, вероятно, понизить шумовую температуру приемного тракта радиометра, например, использовать охлаждаемые системы, поскольку увеличение времени накопления сигнала свыше 2 часов представляется нецелесообразным.

Литература

Жевакин С.А., Наумов А.П. Поглощение сантиметровых и миллиметровых радиоволн атмосферными парами воды. // Радиотехника и электроника, 1964, т.9, №8, с.1327-1337.

Стерлядкин В.В., Косов А.С. Определение вертикального профиля концентрации водяного пара в атмосфере до 80 км по радиопросвечиванию трассы спутник-земля. // Исследование Земли из космоса. №3, 2014.

Krum D.L. Stratospheric thermal emission and absorption near the 22.235 Gc/s (1.35 cm) rotational line of water vapor. // Journal of Atmospheric and Terrestrial Physics, 1965, v.27, pp.217-238.

Способ определения концентрации газов в атмосфере, основанный на измерении собственного излучения атмосферы и фона на некотором наборе частот в окрестности линии поглощения измеряемого газа, вычислении расчетных значений собственного излучения атмосферы и фона на основе априорных или стандартных данных о вертикальном профиле температуры, атмосферного давления, концентрации измеряемого газа, излучения фона, расчете отклонения профиля измеряемого газа от стандартного по различию между измеряемыми и расчетными значениями собственного излучения на выбранном наборе частот, отличающийся тем, что для получения концентрации измеряемого газа на заданной высоте измеряют разность собственного излучения (дифференциальный сигнал) на первой паре частот, расположенных на низкочастотном склоне линии поглощения измеряемого газа, которая соответствует задан ной высоте, измеряют такую же разность на второй паре частот, расположенных на высокочастотном склоне той же линии, а по отклонению линейной комбинации разностных (дифференциальных) сигналов от ее расчетного значения для стандартных атмосферы и фона вычисляют концентрацию газа на заданной высоте.