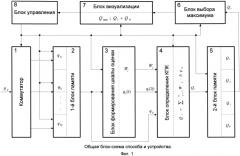
Способ и устройство выбора предпочтительного средства защиты информации

Способ и устройство выбора предпочтительного средства защиты информации

Иллюстрации

Показать все

Реферат

Изобретение относится к цифровой вычислительной технике, а именно к цифровым вычислительным системам для определения качества сравниваемых сложных систем, средств, изделий и различных объектов или их вариантов, описываемых значительным числом разнородных единичных показателей. При невозможности или большом затруднении установления важности свойств (характеристик) сравниваемых объектов или их вариантов и отсутствии обучающей выборки для формирования шкалы оценки предлагается использовать исходные данные самой оцениваемой выборки при определении предпочтительного объекта, средства, варианта.

Изобретение может быть использовано в военной отрасли - для планирования, разработки, создания и приема на вооружение более совершенных систем и средств вооружения, а в гражданской - более качественных и конкурентоспособных систем и изделий.

Техническим результатом является расширение арсенала технических средств для повышения эффективности и качества объектов за счет использования способа и создания устройства выбора предпочтительного из ряда сравниваемых на разных этапах его жизненного цикла без привлечения высококвалифицированных экспертов.

Выбор предпочтительного средства связан с решением многокритериальной задачи. Рассмотрим несколько известных способов ее решения.

1. Известен способ, основанный на использовании метода анализа иерархий [1] и его модификаций. Применение указанного способа предусматривает возможность установления соотношения характеристик сравниваемых средств:

- свойства или характеристики оцениваемых средств одинаково значимы и важны;

- одно свойство или характеристика несколько важнее другого;

- одно свойство или характеристика важнее другого;

- одно свойство или характеристика явно важнее других;

- одно свойство или характеристика абсолютно важнее других.

При возможности установления таких соотношений задача сводится к нахождению коэффициентов весомости W_j и объединению нормированных единичных показателей в комплексный Q=f(W_j, q_j). Однако при наличии у рассматриваемых средств явно разнородных свойств (характеристик) становится невозможным использование метода иерархий и его модификаций.

2. Известны способы нахождения коэффициентов весомости с помощью методов ранжирования [2, 3] характеристик сравниваемых средств, ставящие в затруднение экспертов в случае разнородности свойств.

3. Известны экспертные способы оценки качества рассматриваемых средств [3-5], основанные на упрощении первых двух методов. Это способы, связанные с лексикографическим методом, с методом усреднения единичных показателей, максиминным методом оценки качества, методом идеальной точки и другими.

Всем рассмотренным способам выбора предпочтительного средства присущи погрешности экспертных систем, связанные с наличием «субъективизма».

4. Известны и другие изобретения [8-11] оценки качества объектов, не решающие сформулированную авторами задачу разработки способа выбора предпочтительного средства без привлечения высококвалифицированных экспертов в условиях отсутствия обучающей выборки.

5. Известен способ [6, 7], основанный на формировании обучающей выборки для создания шкалы оценки качества, который позволяет сравнить изделия оцениваемой выборки. Его основной недостаток - требование наличия значительного объема обучающей выборки. Другой недостаток связан с формированием широкой шкалы оценки от худшего эталона Э_х качества до лучшего Э_л. Во-первых, нижняя часть шкалы в районе худшего эталона представляет определенный интерес при выборе худших по качеству систем и средств. Во-вторых, наличие в шкале оценки худшего эталона снижает достоверность оценки при выборе предпочтительного варианта из выборки высококачественных изделий.

С целью повышения объективности и достоверности оценки качества рассматриваемых средств авторами предлагается использовать оцениваемую выборку, состоящую из нормированных единичных показателей качества, позволяющих создать два эталона Э_с - со среднестатистическим уровнем качества и Э_л - уровнем лучшего качества. На основе их использования из всей совокупности оцениваемых средств выбрать предпочтительный объект, обладающий наибольшим комплексным показателем качества.

1. Способ и устройство выбора предпочтительного средства защиты информации, заключающийся в том, что коммутируют информацию о единичных показателях сравниваемых средств, записывают ее в первый блок памяти, отличающийся тем, что ее пересылают в блок формирования шкалы оценки с определением среднестатистического и лучшего уровней качества, образующих соответственно начало и конец прямой, определяющей шкалу оценки качества, проводят плоскости перпендикулярно к этой прямой через точки координат сравниваемых средств в пространстве единичных показателей, находят параметры точек пересечения плоскостей со шкалой оценки, значения которых и образуют комплексные показатели качества сравниваемых средств, максимальная величина одного из них соответствует предпочтительному средству (фиг.1).

Сущность способа нагляднее всего проиллюстрировать на примере сравнения объектов, обладающих разнородными характеристиками (свойствами). К таким относятся средства защиты информации (СЗИ), единичные показатели которых приведены в таблице 1.

В качестве обучающей выборки (ОбВ) используем саму оцениваемую выборку (ОцВ). Для проведения оценки качества разнородные показатели СЗИ в таблице 1 приводим к безразмерному виду. После нормирования

q j = X j / X j max , i = 1,3 ¯ ; j = 1,10 ¯

они принимают значения, указанные в таблице 2.

Таблица 1
Исходные данные для сравнительной оценки СЗИ
Показатель СЗИ, размерность	Средства защиты информации
СЗИ1	СЗИ2	СЗИ3
X1	Наличие средств аутентификации (идентификации), балл	5	4	3
X2	Наличие средств разграничения доступа к ресурсам, балл	3	4	3
X3	Наличие средств криптографической защиты, балл	1	1	5
X4	Наличие средств контроля целостности, балл	4	3	2
X5	Наличие средств управления механизмами защиты, балл	3	4	5
X6	Уровень гарантий защиты (сети, ОС, СУБД и СПО), количество уровней	4	4	1
X7	Интеграция с другими СЗИ, вероятность	0.75	0.85	0.9
X8	Средства оповещения, протоколирования и анализа журналов регистрации (есть/нет)	0	1	1
X9	Наличие Flash-memory (есть/нет)	1	0	1
X10	Количество лицензий на вид деятельности, количество	3	2	4

Таблица 2
Нормированные ЕП qj для оценки качества СЗИ
Нормированные показатели СЗИ	Средства защиты информации
СЗИ1	СЗИ2	СЗИ3
q1	Наличие средств аутентификации (идентификации)	1	0.8	0.6
q2	Наличие средств разграничения доступа к ресурсам	0.75	1	0.75
q3	Наличие средств криптографической защиты	0.2	0.2	1
q4	Наличие средств контроля целостности	1	0.75	0.5
q5	Наличие средств управления механизмами защиты	0.6	0.8	1
q6	Уровень гарантий защиты (сети, ОС, СУБД и СПО)	1	1	0.25
q7	Интеграция с другими СЗИ	0.83	0.94	1
q8	Средства оповещения, протоколирования и анализа	0	1	1
q9	Наличие Flash-memory	1	0	1
q10	Количество лицензий на вид деятельности	0.75	0.5	1

Обязательным условием нормирования является рост комплексного показателя качества (КПК) с ростом его единичных показателей (ЕП).

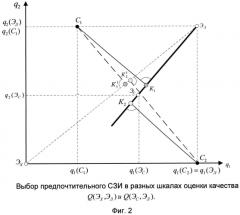
Суть предлагаемой шкалы Q(Э_с, Э_л) оценки качества и недостатки расширенной шкалы Q(Э_х, Э_л) проиллюстрируем на примере двух СЗИ C₁ и C₂ в пространстве двух ЕП с помощью рисунка (фиг.2).

Точки K 1 ' , K 2 ' пересечения перпендикуляров из оцениваемых точек C₁ и C₂ с прямой Э_хЭ_л (расширенной шкалой Q(Э_х, Э_л) оценки качества) говорят о предпочтительности по качеству СЗИ₂>СЗИ₁, т.к. K 2 ' ближе, чем K 1 ' , к лучшему эталону Э_л. Другими словами, в расширенной шкале оценки качества {Э_х, Э_л} КПК Q(СЗИ₂)>Q(СЗИ₁).

При переходе к другой предлагаемой шкале {Э_с, Э_л} оценки качества видно, что СЗИ поменялись ролями. Точки K₁, K₂ на шкале Q(Э_с, Э_л) говорят о предпочтительности по качеству СЗИ₁>СЗИ₂, т.к. К₁ ближе, чем K₂, к лучшему эталону Э_k. Следовательно, КПК Q(СЗИ₁)>Q(СЗИ₂) в шкале {Э_с, Э_л} оценки качества и первое СЗИ предпочтительнее второго. Таким образом, предлагаемая верхняя (правая) часть шкалы оценки {Э_с, Э_л} по сравнению с прежней расширенной шкалой оценки {Э_х, Э_л} уточнила предпочтительность иного, первого средства, по сравнению со вторым СЗИ₂.

Безусловно, верным остается и альтернативное предложение использования левой (нижней) {Э_х, Э_с} расширенной шкалы оценки {Э_х, Э_л}. В этом случае достоверность определения худшего изделия также возрастает.

После убедительного доказательства перехода от первой расширенной шкалы {Э_х, Э_л} ко второй {Э_с, Э_л} на элементарном примере в двумерном пространстве ЕП перейдем к математическому обоснованию использования шкалы оценки качества {Э_с, Э_л} на примере трех СЗИ с 10 ЕП, приведенными в таблице 2 нормированных значений ЕП.

Для удобства определения предпочтительного СЗИ из ряда альтернативных разобьем процесс оценки на ряд этапов.

1. Геометрический смысл оценки качества средств защиты информации. Выбор КПК начинается с формирования шкалы оценки качества в виде прямой Э_сЭ_л, соединяющей точки среднестатистического эталона Э_с, сформированного из ЕП оцениваемых СЗИ, и лучшего эталона Э_л в пространстве оцениваемых ЕП q_j, j=1,…, k=10 (см. фиг.2 для k=2). Если начало шкалы будет представлять среднестатистический эталон Э_с качества, а конец шкалы - эталон Э_л с лучшими значениями ЕП, то прямая Э_сЭ_л будет представлять новую прогрессивную шкалу оценки качества.

«Прогрессивной» шкала {Э_с, Э_л} оценки качества по сравнению со шкалой {Э_х, Э_л} названа по следующим причинам:

- во-первых, нижняя (левая) часть шкалы в районе худшего эталона Э_х качества представляет определенный интерес только при выборе худших по качеству систем и средств (нам же приходится решать обратную задачу выбора предпочтительного среди альтернативных средств, вариантов);

- во-вторых, переход к новой шкале оценки эталона повышает достоверность оценки при выборе предпочтительного варианта из выборки высококачественных изделий, как показано на фиг.2;

- в-третьих, переход к верхней (правой) части шкалы оценки качества от среднестатистического эталона Э_с до лучшего по качеству Э_л с выбором предпочтительного СЗИ в этой области будет напрямую способствовать прогрессу совершенствования СЗИ или других оцениваемых средств, изделий, вариантов.

Через точку C₁ в пространстве ЕП первого СЗИ проведем плоскость (при k=2 - прямую C₁K₁) перпендикулярно прямой Э_сЭ_л. Точка пересечения K₁ этой плоскости с указанной прямой будет определять меру качества Q(K₁) первого СЗИ₁.

Осуществив аналогичную операцию со следующим оцениваемым СЗИ₂ (точка C₂), определяем другую точку K₂. Из фиг.2 видно неравенство

Q(СЗИ₁)>Q(СЗИ₂), которое свидетельствует о предпочтительности по качеству первого СЗИ₁ по отношению ко второму

СЗИ₁>СЗИ₂.

2. Формирование прогрессивной шкалы оценки СЗИ в пространстве ЕП q_j, j=1, k эталонов Э_с и Э_л согласно таблице 2 упрощается по причине возрастания КПК с ростом ЕП. Поэтому лучшему СЗИ_л придаются значения их наибольших величин (строка 2 таблицы 3). Среднестатистический гипотетический эталон Э_с с ЕП достигнутого уровня качества формируется по формуле

q j ( Y / с ) = N − 1 ∑ i = 1 N q i j ( C С , E \ ) ,   j = 1,   k = 10,   N = 3.                                                                                                                                               ( 1 а )

По формуле (1а) вычисляется каждый j-й единичный среднестатистический показатель качества от 1-го до 10 (j=1, к=10) эталона Э_с. Для нашего случая усреднение осуществляется по трем оцениваемым СЗИ, например для 1-го ЕП (1-я строка таблицы 2)

q 1 ( Э с ) = ( 1 + 0.8 + 0.6 ) / 3 = 0.8.                                                                                                                                                                                                         ( 1 б )

Значение q₁=0.8 заносится в таблицу 3 (1-я строка, столбец 1). По аналогии с формулой (16) вычисляются остальные значения, например q_j, j=2, k=10, которые заносятся во 2, 3, …, k-й столбцы 1-й строки табл.3.

Направление прямой Э_сЭ_л прогрессивной шкалы оценки качества в пространстве ЕП описывается уравнениями

Δ q j ( Э с Э л ) = q j ( Э л ) − q j ( Э с ) , j = 1, … , k ,                                                                                                                                                                         ( 2 а )

значения которых занесены в 3-ю строку табл.3.

Таблица 3
Значения ЕП гипотетических эталонов Эс, Эл и коэффициентов весомости Wj(Эс, Эл), Wj (Эх, Эл)
№	ЕП	q1	q2	q3	q4	q5	q6	q7	q8	q9	q10
		1	2	3	4	5	6	1	8	9	10
1	qj(Эс)	0.8	0.833	0.467	0.75	0.8	0.75	0.923	0.667	0.667	0.75
2	qj(Эл)	1	1	1	1	1	1	1	1	1	1
3	Δqj(Эс, Эл)	0.2	0.167	0.533	0.25	0.2	0.25	0.077	0.333	0.333	0.25
4	Wj(Эс, Эл)	0.248	0.207	0.66	0.31	0.248	0.31	0.095	0.413	0.413	0.31
5	Wj(Эх, Эл)	0.097	0.061	0.195	0.121	0.097	0.182	0.041	0.243	0.243	0.121
6	Δqj(C1)	0.2	-0.083	-0.267	0.25	-0.2	0.25	-0.093	-0.667	0.333	0
7	Δqj(C2)	0	0.167	-0.267	0	0	0.25	0.017	0.333	-0.667	-0.25
8	Δqj(C3)	-0.2	-0.083	0.533	-0.25	0.2	-0.5	0.077	0.333	0.333	0.25

3. Уравнения прямой в пространстве ЕП. Геометрический смысл построения шкалы оценки заключается в построении прямой, проходящей через точки Э_с и Э_л, как показано на фиг.2 в двумерном пространстве ЕП. ОбВ, сформированная из двух эталонов, описывается симметричными (каноническими) [12] уравнениями

( q 1 − q c 1 ) / ( q е 1 − q c 1 ) = … = ( q j − q c j ) / ( q е j − q c j ) = … = ( q k − q c k ) / ( q е k − q c k ) = Q ,   k = 10             ( 2 б )

Переход с введением параметра 0 позволяет переписать формулу (2б) в несколько ином виде

q j = Δ q j Q + q c j ,   j = 1, … , k .                                                                                                                                                                                                                                                   ( 3 )

Согласно значениям ЕП (строка 1) таблицы 3 конкретизация формулы (3) для эталона Э_с будет выглядеть следующим образом

q 1 = 0.2 Q + 0.8 ; q 2 = 0.167 Q + 0.833 ; q 3 = 0.533 Q + 0.467 ; q 4 = 0.25 Q + 0.75 ; q 5 = 0.2 Q + 0.8 ;                                                                                                                                                                                                                                                                                                           ( 3 а ) q 6 = 0.25 Q + 0.75 ; q 7 = 0.077 Q + 0.923 ; q 8 = 0.333 Q + 0.667 ; q 9 = 0.333 Q + 0.667 ; q 10 = 0.25 Q + 0.75 ;

Нетрудно заметить, что при Q=0 уравнения (3а) составляют в пространстве ЕП координаты q_j(Э_с) среднестатистического средства СЗИ_с точки Э_с (см. 1-ю строку таблицы 3). При Q=1 уравнения (3а) представляют в пространстве ЕП координаты q_j(Э_л) лучшего гипотетического средства СЗИ_л точки Э_л (см. 2-ю строку таблицы 3).

4. Уравнение плоскости P₁ в пространстве ЕП, проходящей через точку C₁, записывается в виде

∑ j = 1 k ( Δ q j q j − q 1 j ) = 0,   j = 1, k ¯ .                                                                                                                                                                                                                                   ( 4 )

Прохождение плоскости P₁ перпендикулярно прямой Э_сЭ_л через точку C₁ требует, во-первых, в уравнении (4) введения g_j(C₁) их значений в параметрической форме

q j = Δ q j Q 1 + q c j ,                                                                                                                                                                                                                                                                                             ( 3 б )

во-вторых, равенства Δq_j=q_лj-q_cj и, в-третьих, замены в формуле (3а) параметра Q на Q₁

∑ j = 1 k Δ q j ( Δ q j Q 1 − q 1 j ) = 0,   j = 1, k ¯ .                                                                                                                                                                                                                                   ( 4 a )

5. Определение пересечения плоскости P₁ с прямой Э_сЭ_л связано с преобразованием уравнения (4а) и нахождения значения Q₁

∑ j = 1 k Δ q j ( Δ q j Q 1 + q c j − q 1 j ) = Q 1 ∑ j = 1 k Δ q j 2 + ∑ j = 1 k Δ q j ( q c j − q 1 j ) = 0 ;                                                                                                 ( 4 б )

Q 1 = ∑ j = 1 k Δ q j ( q 1 j − q c j ) / ∑ j = 1 k Δ q j 2 = ∑ j = 1 k W j ( q 1 j − q c j ) ,                                                                                                                     ( 5 )

W j = Δ q j / ∑ j = 1 k Δ q j 2 .                                                                                                                                                                                                                                                                                         ( 5 а )

Анализ уравнений (5), (5a) показывает:

- точка K₁ пересечения плоскости P₁, проходящей через точку C₁, с прямой Э_сЭ_л характеризуется величиной Q₁, определяемой ЕП q_1j(C₁);

- при движении точки K₁ вдоль прямой Э_сЭ_л на интервале Э_с, Э_л значение Q₁ находится в пределах от нуля до единицы 0=Q₁(Э_с)≤Q₁(K₁)≤Q₁(Э_л)=1. В начальной точке шкалы оценки, когда K₁→Э_с, q_1j=q_cj и, как следует из формул (5), (5а) Q₁(K₁)=Q₁(Э_с)=0 только в случае q_1j-q_cj=0. В конечной точке шкалы оценки, когда K₁→Э_л, q_1j=q_лj и, как следует из формул (5), (5а) Q₁(K₁)=Q₁(Э_л)=1 только в случае q_лj-q_cj=Δq_j;

- отсюда следует важный вывод, что прямая Э_сЭ_л может служить шкалой оценки качества, а величина Q₁(K₁) - мерой качества, т.е. комплексным показателем качества (КПК) Q.

Отметим, что при попадании точки K_i на шкалу оценки качества Q(K_i) левее точки Э_с знак КПК становится отрицательным. Это говорит о том, что оцениваемое средство СЗИ нах