Способ определения модуля скорости аэродинамической цели
Иллюстрации
Показать всеИзобретение относится к радиолокации и может быть использовано в радиолокационных станциях (РЛС) с грубыми измерениями азимута и угла места. Достигаемый технический результат - повышение точности определения модуля скорости аэродинамической цели (АЦ). Указанный результат достигается за счет того, что формируют фиксированную выборку значений квадратов дальности, оценивают второе приращение квадрата дальности за обзор путем оптимального взвешенного суммирования значений квадратов дальности, делят эту оценку на период обзора РЛС во второй степени и получают значение квадрата модуля скорости АЦ, летящей по линейной траектории. Повышение точности определения модуля скорости достигается за счет устранения влияния ошибок измерения азимута и угла места. 4 ил.
Реферат
Изобретение относится к способам траекторной обработки радиолокационной информации и может быть использовано в РЛС и в автоматизированных системах управления радиолокационных подразделений.
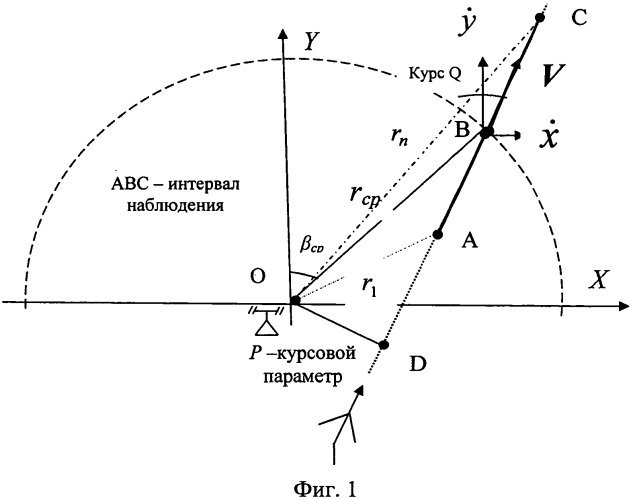
Общим в известных способах является то, что для определения модуля скорости аэродинамической цели (АЦ), называемого также, согласно ГОСТ 20058-80, воздушной скоростью, вычисляют оценки, то есть численные значения, составляющих вектора скорости по направлениям осей выбранной системы координат по выборкам радиолокационных измерений координат (Динамика летательных аппаратов. Термины, определения и обозначения. ГОСТ 20058-80. Госкомитет СССР по стандартам. М: Изд-во стандартов, 1981). В частности, в местной прямоугольной декартовой системе координат OXYZ (смотри фиг.1), начало которой находится в точке стояния РЛС, ось OY направлена в заданную точку (например, на север), ось OZ направлена по отвесной линии от земной поверхности, ось ОХ находится в одной плоскости с осью OY и образует с ней угол 90°, модуль скорости V аэродинамической цели, летящей по линейной траектории с постоянной скоростью, на постоянной высоте и с произвольным постоянным курсом относительно неподвижной РЛС, равен квадратному корню из суммы квадратов оценок скорости изменения декартовых координат x ˙ ^ и y ˙ ^ : V = x ˙ ^ 2 + y ˙ ^ 2
Между собой известные способы отличаются типом используемых алгоритмов оценивания скорости изменения декартовых координат и устройствами, реализующими эти алгоритмы. По типу алгоритмов способы можно разделить на две группы.
К первой группе относятся способы, в которых используются рекуррентные алгоритмы последовательной фильтрации (Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - М.: «Сов. радио», 1978, с. 48-72, с. 109-118; Кузьмин С.З. Цифровая обработка радиолокационной информации - М.: «Сов. радио», 1967, с. 317-340). Сущность работы алгоритмов заключается в том, что оценки (сглаженные значения) скорости изменения координаты в очередном (n-м) обзоре определяются по предыдущим (полученным в n-1 обзоре) сглаженным значениям и результатом последнего (в n-м обзоре) измерения координаты. Поэтому независимо от числа измерений используются только два числа: предыдущая оценка и результат последнего измерения. Одним из недостатков является низкая устойчивость. При больших выборках измерений наступает явление расходимости и ошибки фильтрации резко возрастают. Без принятия специальных мер обеспечения устойчивости - такие алгоритмы непригодны для практического использования в автоматизированных системах вторичной (трассовой) обработки радиолокационной информации. (Кузьмин С.З. Основы проектирования истем цифровой обработки радиолокационной информации - М.: «Радио и связь», 1986, с.167-169; Жданюк Б.Ф. «Основы статистической обработки…», с. 57-66).
Во второй группе для определения численных значений скорости изменения координаты используются результаты всех измерений, произведенных на интервале наблюдения, то есть формируется фиксированная выборка радиолокационных измерений. Ко второй группе относятся следующие алгоритмы оценивания:
алгоритмы оценивания методом скользящего дифференцирования (Жданюк Б.Ф. «Основы статистической обработки…», с.253-265);
алгоритмы оценивания с использованием линейной комбинации ортогональных полиномов Чебышева (там же, с.109-142);
алгоритмы оценивания путем оптимального взвешенного суммирования значений декартовых координат (Кузьмин С.З. «Цифровая обработка радиолокационной информации», с.298-306).
По сущности технического решения наиболее близким аналогом заявляемому способу, то есть прототипом, является способ, в котором для определения модуля скорости находят оценки скорости изменения декартовых координат (составляющих вектора скорости) путем оптимального взвешенного суммирования вычисленных на интервале наблюдения значений декартовых координат, вычисляют сумму квадратов этих оценок, вычисляют квадратный корень из этой суммы.
В способе, принятом за прототип, производят преобразование измеренных значений дальности r, азимута β и угла места ε в горизонтальные декартовы координаты x и y:
xi=ricosεisinβi;
yi=ricosεicosβi.
Затем по выборкам из n преобразованных координат раздельно и независимо находят оценки Δ 1 x ^ и Δ 1 y ^ первого приращения этих координат за обзор:
Δ 1 x ^ = ∑ i = 1 n η Δ 1 x ^ ( i ) x i
Δ 1 y ^ = ∑ i = 1 n η Δ 1 y ^ ( i ) y i
где η Δ 1 x ^ ( i ) = η Δ 1 y ^ ( i ) = 6 ( 2 i − n − 1 ) n ( n 2 − 1 ) - весовые коэффициенты оптимального оценивания первого приращения координаты за период обзора Т0 (Кузьмин С.З. Основы проектирования систем цифровой обработки радиолокационной информации - М.: «Радио и связь», 1986, с.151).
Полученные оценки делят на период обзора, в результате чего находят оценки скорости изменения декартовых координат. После суммирования квадратов этих оценок и вычисления квадратного корня из полученной суммы определяют значение модуля скорости V.
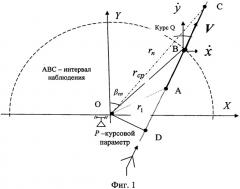
Принцип работы устройства определения модуля скорости способом-прототипом по выборке из трех значений декартовых координат поясняется схемой, приведенной на фиг.2. В состав устройства входят блок 1 преобразования измеренных координат, два блока оценивания первого приращения горизонтальных координат (блоки 2, 7), два блока оценивания скорости изменения координат путем деления оценок приращения координаты на период обзора (блоки 3, 8), два блока вычисления квадратов оценок скорости изменения координат (боки 4, 9), сумматор (блок 5), блок 6 вычисления квадратного корня из суммы квадратов оценок скорости изменения координат. Выход блока 6 является выходом устройства.
Оценивание скорости изменения декартовой координаты x производят следующим образом. На входы умножителя блока 1 преобразования координат подают измеренные значения дальности, вычисленные значения синусов измеренных азимутальных углов и вычисленные значения косинусов измеренных значений угла места. Полученное на выходе умножителя блока 1 значение декартовой координаты x в текущем обзоре подают на вход первой линии задержки (ЛЗ) блока 2 оценивания первого приращения, а также умножают на весовой коэффициент и подают на вход сумматора. Значения декартовых координат, полученные в двух предыдущих обзорах, после задержки в двух линиях задержки на время, равное одному и двум периодам обзора (Т0 и 2Т0), умножают на свои весовые коэффициенты и одновременно с текущим взвешенным значением координаты подают на вход сумматора. Выход сумматора является выходом блока 2 вычисления оценок первого приращения горизонтальной координаты x.
Для формирования фиксированной выборки из n значений декартовой координаты в состав блока должны входить n-1 линий задержек и умножителей.
При оценивании приращения координаты в цифровой вычислительной машине (ЦВМ) запоминание координат производится в оперативном запоминающем устройстве, заранее вычисленные весовые коэффициенты в виде констант хранятся в долговременном запоминающем устройстве, а операция суммирования производится в арифметическом устройстве ЦВМ (Кузьмин С.З. Цифровая обработка радиолокационной информации. М: «Радио и связь», 1967, с.303-304).
Далее оценку первого приращения делят на период обзора в блоке 3, то есть получают оценку скорости изменения координаты x, эту оценку возводят во вторую степень в блоке 4 и подают на первый вход сумматора 5. На второй вход сумматора подают квадрат оценки скорости изменения координаты y. Эту оценку вычисляют аналогичным способом в блоках 7 и 8 за исключением того, что на вход умножителя блока 1 преобразования координат подают вычисленные значения косинусов измеренных азимутальных углов. После вычисления квадратного корня из этой суммы в блоке 6 определяют значение модуля скорости аэродинамической цели на линейной траектории.
Среднеквадратические ошибки (СКО) определения модуля скорости вычисляют по формуле
σ V ^ ( x , y ) = 1 T 0 12 n ( n 2 − 1 ) [ ( P σ β ) 2 + ( r c p sin ε c p σ ε ) 2 + ( cos ε c p σ r ) 2 ] ,
где P = r c p | sin ( β c p − Q ) | - курсовой параметр или минимальное удаление траектории от РЛС;
rcp, βcp, εcp - дальность АЦ в точке оценивания (в середине интервала наблюдения), ее азимут и угол места;
σr, σβ, σε - СКО измерения дальности, азимута и угла места;
Q - курс АЦ.
Как видно из формулы, СКО определения модуля скорости практически не зависит от ошибок измерения дальности σr. Ошибки измерения угла места σε оказывают существенное влияние на СКО определения модуля скорости, если высота АЦ zcp=rcpsinεcp соизмерима с величиной курсового параметра P. Доминирующее влияние оказывают ошибки измерения азимута σβ, если курсовой параметр больше высоты. Кроме того, величина СКО определения модуля скорости зависит от периода обзора Т0 и количества измерений n в обрабатываемой выборке, то есть от величины времени оценивания tоц=(n-1)Т0.
В качестве примера в таблице приведены значения СКО оценивания модуля скорости самолета, летящего с курсом Q=90° (параллельно оси ОХ) на высоте 10 км. Принимается, что время оценивания - 60 секунд (период обзора Т0=10 с, количество измерений n=7), дальность цели в середине интервала наблюдения rср=100 км, СКО измерения азимута и угла места σβ=σε=1°. Оценивание скорости производится при четырех значениях азимута (βcp=0°, 30°, 60° и 90°). В этом примере курсовые параметры вычисляются по формуле P = r c p | sin ( β c p − 90 ∘ ) | = r c p | cos β c p | .
| Азимут АЦ | 0° | 30° | 60° | 75° | 90° |
| Курсовой параметр P, км | 100 | 87 | 50 | 26 | 0 |
| σ V ^ ( x , y ) , м/с | 33 | 29 | 16 | 9,2 | 3,3 |
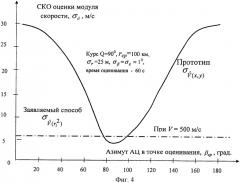
Как видно из таблицы, точность оценивания модуля скорости АЦ, летящей с большими (50-100 км) курсовыми параметрами относительно РЛС, уменьшается в 5-10 раз по сравнению с оцениванием при радиальном курсе (Q=βср). Доминирующее влияние оказывают ошибки измерения азимута. Характер зависимости СКО оценивания модуля скорости от азимута показан также на графике фиг.4. Как видно из графика, СКО σ V ^ ( x , y ) минимальна, когда азимут равен 90°, то есть при радиальном курсе.
Большие ошибки измерения азимута и угла места характерны для РЛС, в которых размеры антенны соизмеримы с длиной волны, в частности для РЛС метрового и примыкающего к нему участка дециметрового диапазона волн. Существенно уменьшить погрешности измерения азимута и угла места в этих РЛС практически невозможно из-за ограниченных размеров антенны. Так как размеры антенны d соизмеримы с длиной волны λ излучаемого РЛС сигнала, ширина диаграммы направленности антенны θ = λ d и СКО измерения азимута σ β = θ π q в несколько раз, а то и на порядок, больше, чем в РЛС сантиметрового диапазона при одинаковом отношении q энергии сигнала к спектральной плотности шума на входе приемника (Теоретические основы радиолокации, под ред. Я.Д. Ширмана. «Сов. Радио», М., 1970, с.290, 291). Поэтому основным недостатком прототипа и других аналогов является низкая точность определения модуля скорости в РЛС, размеры антенн которых соизмеримы с длиной волны.
В то же время ошибки измерения дальности не зависят от размеров антенны. Основными факторами, влияющими на точность измерения дальности, являются ширина полосы частот излучаемого и принимаемого сигналов, величина отношения сигнал/шум и метод обработки сигналов. Однако в прототипе и в других аналогах повышение точности измерения дальности практически не влияет на точность определения модуля скорости.
В связи с этим, целью настоящего изобретения является разработка нового способа определения модуля скорости АЦ, в котором устраняется влияние ошибок измерения азимута и угла места на точность определения модуля скорости за счет использования высокоточных измерений дальности.
В заявляемом способе, в отличие от аналогов, во-первых, при преобразовании координат вычисляют квадраты измеренных значений дальности цели, формируют фиксированные выборки значений квадратов дальности. Измерения азимута и угла места не используют. Во-вторых, находят оценки второго приращения квадратов дальности за период обзора путем оптимального взвешенного суммирования квадратов дальности:
Δ 2 r ^ i 2 = ∑ i = 1 n η Δ 2 r ^ i 2 ( i ) r i 2
Весовые коэффициенты оценки второго приращения вычисляются по формуле
η Δ 2 r ^ i 2 ( i ) = 30 n ( n 2 − 1 ) ( n 2 − 4 ) [ ( n + 1 ) ( n + 2 ) − 6 i ( n + 1 ) + 6 i 2 ]
(Кузьмин С.З. Основы проектирования систем цифровой обработки радиолокационной информации. - М: «Радио и связь», 1986, с.155).
После деления этой оценки на период обзора во второй степени получают значение квадрата модуля скорости:
V ^ 2 ( r i 2 ) = Δ 2 r ^ i 2 T 0 2 = 1 T 0 2 ∑ i = 1 n η Δ 2 r ^ i 2 ( i ) r i 2
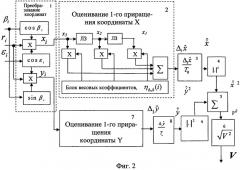
Принцип работы устройства определения модуля скорости заявляемым способом по выборке из трех измерений дальности поясняется схемой, приведенной на фиг.3. В состав устройства входят блок 1 преобразования измеренных координат, то есть вычисления квадрата дальности, блок 2 оценивания второго приращения квадрата дальности, блок 3 деления оценки второго приращения на период обзора в квадрате и блок 4 вычисления квадратного корня из полученного результата. Выход блока 4 является выходом устройства.
Устройство определения модуля скорости заявляемым способом работает следующим образом. Полученные на выходе блока 1 значения квадратов дальности подают на вход блок 2 оценивания второго приращения квадрата дальности, который построен по одинаковой схеме с блоками 2 и 8 оценивания первого приращения горизонтальной декартовой координаты способом-прототипом. Отличаются эти блоки только значениями весовых коэффициентов. Значение квадрата дальности в текущем обзоре подают на вход первой линии задержки, а также умножают на весовой коэффициент и подают на вход сумматора блока 2. Значения квадратов дальности, полученные в предыдущих обзорах, после задержки на время, равное одному и двум периодам обзора (Т0 и 2T0), умножают на свои весовые коэффициенты и одновременно с текущим взвешенным значением квадрата дальности подают на вход сумматора. При обработке фиксированной выборки из n значений квадратов дальности в состав блока, так же, как и в прототипе, должны входить n-1 линий задержек и умножителей.
Сигнал с выхода сумматора блока 2 подают на вход блока 3, где производят деление на период обзора в квадрате. После вычисления квадратного корня из полученного результата в блоке 4 получают значение модуля скорости АЦ.
Среднеквадратические ошибки определения модуля скорости заявляемым способом вычисляют по формуле
σ V ^ ( r i 2 ) = r c p σ r V T 0 2 180 n ( n 2 − 1 ) ( n 2 − 4 ) .
(Кузьмин С.З. Основы проектирования.., с.156).
Как видно из формулы, СКО определения модуля скорости, в отличие от аналогов, зависит только от ошибок измерения дальности σr. Кроме того, величина СКО определения модуля скорости зависит от периода обзора Т0, количества измерений n в обрабатываемой выборке и от значения модуля скорости, то есть от длины интервала наблюдения (n-1)T0V и величины времени оценивания (n-1)T0. В отличие от аналогов, измерения азимута и угла места не используются. Поэтому СКО определения модуля скорости не зависит от курсового параметра.
Для сравнения значений СКО оценок скорости заявляемым способом и способом-прототипом вычисляется отношение выражений определения этих СКО, при этом не учитывается незначительное влияние ошибок измерения угла места, а ошибки измерения азимута подставляются в градусах:
σ V ^ ( r i 2 ) σ V ^ ( x , y ) ≈ 222 V n T 0 P r c p × σ r σ β .
Если отношение σ V ^ ( r i 2 ) σ V ^ ( x , y ) меньше единицы, для определения скорости используется заявляемый способ, если больше единицы - известные способы.
В траектории, приведенной в качестве примера для прототипа, СКО определения модуля скорости заявляемым способом равна 5,5 м/с при ошибках измерения дальности σr=25 м/с и скорости АЦ V=500 м/с. Как видно из таблицы и графиков фиг.4, точность определения модуля скорости заявляемым способом повышается в 1,5-6 раз при курсовых параметрах от 25 до 100 км.
Заявляемое изобретение соответствует условиям новизны и изобретательского уровня, так как принципиальные отличия заявляемого способа от прототипа и других аналогов заключаются в следующем:
используются фиксированные выборки квадратов дальности, а не выборки горизонтальных декартовых координат;
производится оценивание второго приращения квадрата дальности, а не оценивание первого приращения декартовых координат;
все операции по определению модуля скорости производятся последовательно во времени (вычисление квадратов дальности, нахождение оценки второго приращения, деление оценки на период обзора в квадрате и вычисление квадратного корня). В прототипе все операции до суммирования квадратов оценок скорости изменения декартовых координат производятся параллельно, поэтому более чем в два раза увеличивается объем аппаратуры и вычислительные затраты:
точность определения модуля скорости зависит только от ошибок измерения дальности, длины интервала наблюдения и времени оценивания. В прототипе доминирующее влияние оказывают погрешности измерения азимута, величина курсового параметра и время оценивания, а ошибки измерения дальности можно не учитывать.
Таким образом, технический результат от использования заявляемого изобретения характеризуется повышением, по сравнению с прототипом и другими аналогами, точности определения модуля скорости аэродинамических целей, летящих с параметром относительно РЛС с грубыми измерениями азимута и высокоточными измерениями радиальной скорости, упрощением устройств определения модуля скорости заявляемым способом и снижением вычислительных затрат.
Способ определения модуля скорости аэродинамической цели, заключающийся в том, что производят преобразование измеренных полярных координат цели, формируют фиксированную выборку значений преобразованных координат, оценивают приращение преобразованной координаты за период обзора РЛС, отличающийся тем, что вычисляют квадраты измеренных значений дальности, формируют фиксированную выборку квадратов дальности, вычисляют оценку второго приращения квадрата дальности за период обзора РЛС путем оптимального взвешенного суммирования значений квадратов дальности, производят деление этой оценки на период обзора во второй степени, из полученного результата вычисляют квадратный корень и получают значение модуля скорости аэродинамической цели, летящей по линейной траектории.