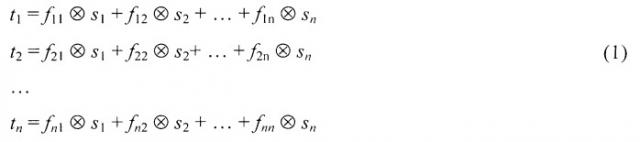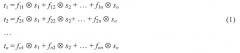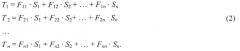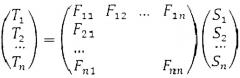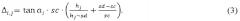Способ реконструкции изображений продольных срезов объекта

Способ реконструкции изображений продольных срезов объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к области обработки изображений, а именно к обработке изображений, полученных методом цифрового томосинтеза. Более конкретно, заявляемое техническое решение относится к способам реконструкции изображений продольных срезов объекта путем преобразования рентгенографических снимков, сделанных под разными углами.

Описание предшествующего уровня техники

В настоящее время для исследования и визуализации внутренней структуры объектов используются различные методы. В медицинской диагностике одним из методов диагностики и визуализации является томографическое исследование, основанное на получении послойного изображения внутренней структуры объекта и его восстановлении при томографической обработке проекций. Для обработки применяют различные математические методы, в результате использования которых решаются различные задачи: повышение устойчивости к шумам, существующих в исходных данных, повышение скорости обработки и, следовательно, уменьшение времени для получения изображений и т.д.

Из уровня техники известны способы получения томографических срезов объекта путем преобразования рентгенографических снимков, сделанных под разными углами.

Одним из самых первых и самых простых способов получения изображения томографических срезов является способ смещения и суммирования Shift-And-Add (SAA), который заключается в суммировании сдвинутых на определенное расстояние проекций объекта (James Т Dobbins III and Devon J Godfrey, Digital x-ray tomosynthesis: current state of the art and clinical potential, 2003 Phys. Med. Biol. 48 R72, section 3.2; doi: 10.1088/0031-9155/48/19/R01,).

Иллюстрацией способа служит фиг.1, где на фиг.1а изображены три положения 1, 2, 3 рентгеновской трубки и проекции круга из плоскости A и треугольника из плоскости B на детекторе; на фиг.1б приведены изображения структур плоскости A или B: четкие изображения структур плоскости A или B могут быть получены с помощью сдвига проекций и их суммирования, структуры вне интересующей плоскости будут размазаны по всему изображению (т.е. размыты).

На фиг.1 видно, как посредством сдвига и суммирования можно получить четкое изображение, например, треугольника из плоскости B: первую проекцию сдвигают вправо относительно центра детектора, центральную проекцию оставляют без изменений, а третью проекцию сдвигают влево. Суммирование трех сдвинутых проекций приводит к наложению треугольников друг на друга, тогда как круги оказываются «размазанными» по всему изображению.

Простейшим применением способа является линейная томография. Способ реализуется следующим образом. В процессе исследования объекта оператор задает определенную высоту размещения рентгеновской трубки над плоскостью детектора. При движении рентгеновской трубки (и ее повороте вокруг оси вращения, находящейся внутри объекта) и движении самого детектора вдоль оси абсцисс в сторону, противоположную направлению движения трубки, получают проекции объекта. Полученные проекции автоматически суммируются, в результате чего получают один томографический срез объекта на заданной оператором высоте. При сравнительно простом алгоритме и небольшом объеме вычислений, что является несомненным преимуществом способа, отрицательной стороной является недостаточно высокое качество получаемых изображений, связанное с сильным наложением деталей изображений из соседних срезов на интересующий томографический срез.

Среди способов реконструкции изображений известен также способ обратных проекций (матриц) Matrix Inversion Tomosynthesis (MITS) (патент US №490320, опубл. 20.02.1990), который можно описать следующим образом.

Положим, что объект состоит из n томографических срезов. Обозначим через t_i изображение i-го томографического среза, полученное методом SAA, где i=1, …, n. С другой стороны каждый томографический срез может быть описан в виде:

где s_j - изображение действительной структуры объекта в томографическом срезе j, где j=1, …, n, а f_ij - функция размытия для изображения действительных структур среза j в срезе i.

Следует отметить, что t_i и s_j в системе уравнений (1) являются полноразмерными изображениями с размерами (X, Y) пикселей. Однако систему уравнений (1) следует решать непосредственно для каждого пиксела с координатами (x, y).

Переход в Фурье-область обеспечивает простую замену оператора свертки на оператор умножения. Для F, S, T - Фурье-спектров f, s и t соответственно получаем

Ввиду сделанного замечания о решении системы уравнений непосредственно для каждого пиксела с координатами (x, y) полученную систему уравнений (2) следует решать относительно пространственных частот kx и ky.

В матричном виде систему уравнений (2) можно записать так:

или

T=F·S.

Применив матричную алгебру, получаем

S=F^-1·Т,

а применив обратное преобразование Фурье к обеим частям выражения, получаем действительную структуру s:

s=FT^-1(S)=FT^-1(F^-1·Т).

Матрица F в данном случае является плохо обусловленной на низких пространственных частотах kx и ky. На нулевых частотах она является вырожденной. Поэтому для качественного восстановления низких и нулевых частот томографических срезов приходится задействовать дополнительные обработки, что является существенным недостатком данного способа. Также к недостаткам следует отнести и тот факт, что способ основан на реконструкциях SAA, что увеличивает не только продолжительность расчетов, но и количество возможных артефактов.

Раскрытие изобретения

Задачей заявляемого технического решения является создание способа, направленного на получение реконструированных изображений более высокого качества с одновременным уменьшением времени выполнения способа.

Сущность изобретения заключается в том, что реконструкция продольных срезов объекта происходит непосредственно по проекциям, исходя из данных геометрии томографической системы.

Технический результат в заявляемом способе реконструкции изображений продольных срезов объекта, который заключается в том, что с помощью томографической системы заданной геометрии выполняют множество проекций объекта, снятых под разными углами, решают систему линейных уравнений с помощью обратных матриц, неизвестными в которой выступают Фурье-образы S изображений реконструируемых срезов, и затем восстанавливают по ним изображения продольных срезов объекта, достигается тем, что в качестве коэффициентов системы линейных уравнений выступают Фурье-образы D дельта-функций от величин смещений для каждой проекции и каждого среза, при этом величину смещения для каждой проекции и каждого среза рассчитывают, исходя из геометрии системы; в качестве свободных членов выступают Фурье-образы P проекций объекта, а Фурье-образы S изображений реконструируемых срезов определяют методом наименьших квадратов с использованием регуляризации по Тихонову по формуле

S=(D^TD+λ·I)^-1·D^TP,

где λ - параметр регуляризации, I - единичная матрица, D^T - транспонированная матрица D.

Осуществление изобретения

Указанные преимущества, а также особенности изобретения поясняются лучшим вариантом его выполнения со ссылками на прилагаемые фигуры. На фигурах изображены:

фиг.1 - схематичное изображение способа смещения и суммирования Shift-And-Add (SAA) - предшествующий уровень техники;

фиг.2 - схематичное изображение способа по заявляемому техническому решению;

фиг.3 - блок-схема алгоритма реконструкции продольных срезов объекта по изобретению.

Томографическая система, реализующая способ, представляет собой установку для линейной томографии, основные принципы работы которой проиллюстрированы на фиг.2. Объект 1 размещают на столе 2. Над столом располагают рентгеновскую трубку 3, которая может двигаться вдоль стола и поворачиваться вокруг оси вращения. Детектор 4, расположенный под столом 2, перемещается согласно геометрии в сторону, противоположную направлению движения трубки так, чтобы центральный луч L от трубки проходил через ось вращения в центр детектора. Тогда за один проход трубки слева направо получают n проекций объекта 1, снятых под разными углами (на фиг.2 показана геометрия съемки для получения трех проекций объекта). В начале работы (шаг 1) трубка 3 и детектор 4 расположены симметрично относительно оси вращения. На данном шаге получают Проекцию 1. Далее (шаг 2) трубка и детектор смещаются в противоположные стороны, получают Проекцию 2 (центральную). На следующем шаге (шаг 3) трубка и детектор снова смещаются, в результате чего получают Проекцию 3. Каждая проекция представляет собой рентгенографический снимок размером dx на dy пикселей, т.е. зависимость яркости от координат (x, y).

Рассмотрим способ реконструкции продольных срезов объекта путем преобразования рентгенографических изображений, сделанных под разными углами к объекту, для чего введем следующие обозначения:

p_i - проекция объекта, где i=1, …, n, n - число проекций;

sd - расстояние от рентгеновской трубки 3 до детектора 4 в центральной проекции;

sc - расстояние от трубки 3 до оси вращения в центральной проекции;

a _i - угол наклона трубки 3 к вертикали в точке оси вращения для каждой проекции p_i;

nx - ширина детектора 4, мм;

dx - ширина изображения, пиксель;

s_j - томографический срез, где j=1, …, m, m - число срезов;

h_j - высота над поверхностью детектора, на которой требуется реконструировать томографический срез s_j.

Расстояния sd от трубки до детектора и sc от трубки до оси вращения в центральной проекции, угол наклона a _i трубки к вертикали в точке оси вращения для каждой проекции p_i, ширина детектора nx в мм, ширина изображения dx в пикселях и сами проекции p_i являются входными параметрами алгоритма.

Пусть требуется реконструировать m томографических срезов. Каждый томографический срез s_j объекта задается высотой h_j над поверхностью детектора и представляет собой, так же, как и любая проекция, рентгенографический снимок размером (dx, dy) пикселей.

Каждый пиксел p_i(x,y) изображения проекции p_i может быть представлен в виде суммы пикселей s_j(x,y) срезов s_j, смещенных относительно друг друга на величину Δ_i,j:

p₁(x,y)=δ(Δ_1,1)⊗s₁(x,y)+δ(Δ_1,2)⊗s₂(x,y)+…+δ(Δ_1,m)⊗s_m(x,y),

где δ - дельта-функция, аргументом которой является величина смещения Δ_i,j, ⊗ - оператор свертки.

Величина смещения Δ_i,j рассчитывается для каждого среза s_j (на высоте h_j) и для каждой проекции p_i (снятой под углом a _i) по формуле

Для работы непосредственно с изображением необходимо перевести смещение в пиксели:

.

Таким образом, получаем систему уравнений (координаты (x,y) опущены)

Переход в Фурье-область обеспечивает простую замену оператора свертки на оператор умножения. Для D_i,j(kx,ky), P_i(kx,ky), S_j(kx,ky) - Фурье-спектров δ(Δ_i,j(x,y)), p_i(x,y), s_j(x,y) соответственно, где kx и ky - пространственные частоты, - система уравнений (4) имеет вид (частоты (kx,ky) опущены)

Перепишем полученную систему уравнений (5) в матричном виде:

или

P=D·S.

Применив матричную алгебру, получаем

а применив обратное преобразование Фурье к обеим частям выражения, получаем искомые томографические срезы объекта:

s=FT^-1(S)=FT^-1(D^-1·P).

Строго говоря, решение данной системы уравнения возможно только при n=m, то есть для квадратной матрицы D. Для того чтобы обойти данное ограничение, т.е. находить решение, когда число проекций не равно числу реконструируемых срезов n≠m, применяется метод наименьших квадратов, который заменяет выражение (6) на:

где D^T - транспонированная матрица D.

Матрица D является плохо обусловленной на низких пространственных частотах kx и ky. На нулевых частотах она является вырожденной. Поэтому для качественного восстановления низких и нулевых частот томографических срезов применяется метод регуляризации по Тихонову (Кирьянов Д.В., Кирьянова Е.Н. Вычислительная физика. - М.: Полибук Мультимедиа, 2006. - 352 с.: ил), который заменяет выражение (7) на:

S=(D^TD+λ·I)^-1·D^TP,

где λ - параметр регуляризации, подбираемый экспериментально, исходя из целей рентгенографического исследования и типа объекта, I - единичная матрица.

Алгоритм описывается блок-схемой, изображенной на фиг.3. После получения массива проекций p_1..n объекта и параметров sd, sc, a _1…n, nx, dx, h_1…m, λ рассчитывают матрицу смещений Δ_{1…n, 1…m} для каждой проекции из массива p_1…n и каждого томографического среза из массива s_1…m на определенной высоте из массива h_1…m по приведенной выше формуле (3). Здесь индекс вида 1…n обозначает одномерный массив (вектор) размерностью n, индекс вида (1…n, 1…m) обозначает двумерный массив размерностями (n, m.)

Далее выполняют преобразование Фурье для каждой проекции из массива p_1…n только по горизонтальным частотам (т.е. в направлении сдвига проекций) и получают вектор Фурье-образов P_1..n, где каждый Фурье-образ есть набор пространственных частот.

Затем выполняют два цикла: i - внешний цикл по строкам (в блок-схеме nf - частота Найквиста), и j - внутренний цикл (в блок-схеме ny - количество столбцов в проекциях p_1..n):

1. в цикле по i в зависимости от пространственной частоты kx_i формируется матрица A_{1…n, 1…m}, которая соответствует Фурье-преобразованию дельта-функции от смещения Δ_{1…n, 1…m}:

A_{1…n, 1…m}=exp(Δ_{1…n, 1…m}·kx_i).

Исходя из метода наименьших квадратов и регуляризации по Тихонову, рассчитывают матрицу Ar

,

где - транспонированная матрица A, I_{1…n, 1…m} - единичная матрица.

2. в цикле по j выбирается вектор B_1…n=P_{ij, 2…n}, соответствующий вектору частот с индексами i и j всех проекций от 1 до n и производится расчет вектора частот с индексами i и j всех томографических срезов от 1 до m:

.

Таким образом получают все частоты пространственного спектра томографического среза S_1…m. Выполняя обратное преобразование Фурье над S_1…m (только по горизонтальным частотам, т.е. в направлении сдвига проекций) получают непосредственно изображение томографического среза s_m.

Таким образом, предлагаемое решение позволяет за счет исключения алгоритма обработки изображений SAA, при использовании которого происходит наложение деталей изображений из соседних срезов на изображение интересующего томографического среза, а также за счет коррекции значений низких и нулевой частот на изображениях томографических срезов, повысить качество реконструированных изображений при одновременном сокращении времени выполнения способа.

Предлагаемый способ реконструкции продольных срезов объекта может быть реализован на базе стандартной аппаратуры, что определяет возможность его широкого применения для томографических исследований в медицине.

Способ реконструкции изображений продольных срезов объекта, заключающийся в том, что с помощью томографической системы заданной геометрии получают множество проекций объекта, снятых под разными углами, решают систему линейных уравнений с помощью обратных матриц, неизвестными в которой являются Фурье-образы S изображений реконструируемых срезов, и затем восстанавливают по ним изображения продольных срезов объекта, отличающийся тем, что в качестве коэффициентов системы линейных уравнений выступают Фурье-образы D дельта-функций от величин смещений для каждой проекции и каждого среза, при этом величину смещения для каждой проекции и каждого среза рассчитывают, исходя из геометрии системы; в качестве свободных членов выступают Фурье-образы P проекций объекта, а Фурье-образы S изображений реконструируемых срезов определяют методом наименьших квадратов с использованием регуляризации по Тихонову по формулеS=(D^TD+λ·I)^-1D^ТP,где λ - параметр регуляризации, I - единичная матрица, D^Т - транспонированная матрица D.