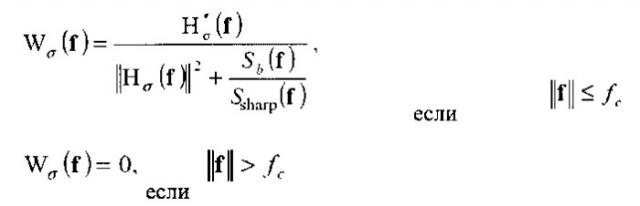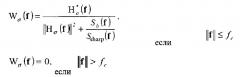Обработка данных изображения, содержащих эффект турбулентности в жидкой среде

Обработка данных изображения, содержащих эффект турбулентности в жидкой среде

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к обработке цифровых данных изображения.

Оно, в частности, направлено на обработку последовательных изображений (обычно последовательности в виде фильма). Такие изображения получают с помощью камеры и, в частности, камера погружена в жидкость, в которой присутствует турбулентность. Например, такие эффекты турбулентности могут возникать, из-за неоднородностей в жидкой среде, таких, как локальные разности температуры. Такие явления турбулентности вызывают эффект видимого смещения пикселей изображений. Например, локальное различие в температуре в области, соответствующей кромке изображения, приводит к явлениям турбулентности, влияние которых на снятые на пленку изображения проявляет себя, как нарушение порядка пикселей на кромке изображения с видимым смещением (относительно исходного положения) некоторых из этих пикселей, такое смещение изменяется с течением времени (случайным образом).

Случайная природа таких изменений приводит к трудностям (или даже невозможности) при обработке изображений, для удаления эффектов турбулентности из них.

Настоящее изобретение направлено на улучшение ситуации.

С этой целью, в нем предложен способ для обработки данных изображения упомянутого выше типа, содержащий, в частности этапы, на которых:

- моделируют эффект турбулентности на пикселях изображений, и

- выполняют обращение свертки с помощью упомянутого моделирования для усредненного по времени изображения.

Предпочтительно, действительно наблюдалось, что возможно идеально смоделировать эффект турбулентности, но в течение относительно длительного периода. Таким образом, усреднение пикселей изображения с течением времени позволяет "подавить" влияние турбулентности. При этом получают усредненное, размытое изображение. Для того чтобы придать этому изображению резкость, к нему применяют обращенную свертку с использованием модели, представляющей эффекты турбулентности.

Конечно, предполагается, что снимаемая с помощью камеры сцена является фиксированной, хотя представленный ниже один вариант осуществления настоящего описания относится к случаю камеры, которая поступательно перемещается относительно статической сцены.

В одном предпочтительном варианте осуществления упомянутое выше моделирование эффектов турбулентности содержит оценку модели h(u) плотности вероятности для вектора u смещения, относящегося к эффекту турбулентности. В частности, наблюдалось, что, особенно предпочтительно, вероятностное моделирование влияния турбулентности на пикселях изображений позволяло идеально решать проблему моделирования прежде случайной турбулентности.

Один пример предпочтительной модели представляет собой экспоненциально уменьшающийся тип и может быть выражен, как функция вектора u с помощью уравнения следующего типа:

h σ ( u ) = A σ 2 exp { − B ‖ u ‖ σ }

где:

σ представляет среднеквадратичное отклонение от нормы вектора u,

A и B представляют собой положительные вещественные константы, такие, что, например A=3/π и B = 6 .

Другие варианты осуществления возможны и будут описаны ниже.

В том, что касается оценки усредненного по времени изображения, в одном возможном варианте осуществления, включено среднее взвешивание на степени фактора забывания (ниже обозначен, как α), с соответствующим уменьшением функции по времени.

Усредненное изображение I_α(x,n), оценка которого была выполнена во время n для пикселя с координатами x вектора, может быть задано следующим образом:

I α ( x , n ) = 1 − α 1 − α n ∑ k = 0 n − 1 α k I ( x , n − k )

член α представляет собой вещественное число, соответствующее фактору забывания.

На практике усредненное по времени изображение может быть оценено, используя рекурсивную временную фильтрацию.

Таким образом, n-тый выход временного фильтра для времени n, обозначенный, как I_f(x,n), и усредненное изображение I_α(x,n) связаны между собой уравнениями:

I f ( x , n ) = α I f ( x , n − 1 ) + ( 1 − α ) I ( x , n )

I α ( x , n ) = 1 1 − α n I f ( x , n )

Выполненные тесты показали, что фактор α забывания был наилучшим, если он был близок к 1, но при этом все еще меньше 1. Выбранное значение, равное 0,99, давало хорошие результаты.

Далее, что касается обращенной свертки, выполняемой при моделировании, применение линейной пространственной фильтрации, предпочтительно, включено с выражением, соответствующим упомянутому выше моделированию.

Пространственная фильтрация, предпочтительно, может представлять собой фильтрацию типа Винера, хотя возможны другие варианты осуществления.

Пространственный фильтр задан, например, в спектральном домене выражением следующего типа:

W σ ( f ) = H σ * ( f ) ‖ H σ ( f ) ‖ 2 + S b ( f ) S s h a r p ( f ) , if ‖ f ‖ ≤ f c если

W_σ(f)=0, if ‖ f ‖ > f c если

где:

- f представляет собой двумерный вектор двух частот, нормированный после двумерного преобразования Фурье,

- f_c представляет собой частоту отсечки фильтра для устранения любой потенциальной спектральной ступенчатости,

- S_b(f) and S_sharp(f), соответственно, представляют собой спектральные плотности мощности шумов и резкого изображения, подлежащего определению, и

- H_σ(f) представляет собой двумерное преобразование Фурье плотности вероятности эффекта турбулентности h(u).

Упрощение этого выражения означало учет пространственного фильтра в соответствии с выражением следующего типа:

W σ ( f ) = H σ ( f ) H σ 2 ( f ) + R B S

где член RBS выражен как функция параметров, выбранных таким образом, что член RBS находится в диапазоне от 10^-2 до 10^-4.

Для соотношения упомянутого выше типа:

h σ ( u ) = A σ 2 exp { − B ‖ u ‖ σ } ,

двумерное преобразование Фурье H_σ(f) плотности вероятности влияния турбулентности h_σ(u), задано следующим образом:

H σ ( f ) = ( 1 + C ( σ ⋅ ‖ f ‖ ) 2 ) − 3 2

где C представляет собой положительную вещественную константу, а σ представляет собой положительное вещественное число, подсчитываемое количеством пикселей.

Используя значения констант A и B, заданных ранее и полностью определяющих двумерное преобразование Фурье H_σ(f), это может быть затем представлено следующим образом:

H σ ( f ) = ( 1 + 2 3 ( π σ ⋅ ‖ f ‖ ) 2 ) 3 2

В частности, выполненные тесты показали, что член σ предпочтительно выбирать в диапазоне от 0 до 30 пикселей.

Как упомянуто выше, настоящее изобретение предоставляет вариант осуществления, в котором камера может быть смещена и может поступательно перемещаться относительно статической сцены. В таком случае представленная выше обработка может быть сохранена, однако, требуется выполнить меры по применению смены положения пикселей изображения в момент времени n-1 к следующему изображению в момент времени n, с последующим учетом скорости смещения камеры.

Таким образом, в данном варианте осуществления, изменение положения предыдущего изображения относительно текущего изображения выполняют для оценки усредненного изображения.

Рекурсивную временную фильтрацию затем выполняют при изменении положения и нормировании и, в одном примерном варианте осуществления, общая обработка содержит следующие этапы:

- для сброса при:

I_f(x,1)=0 N(x,1)=0,

- для рекурсивной временной фильтрации при:

I f ( x , n ) = ( 1 − α ) I ( x , n ) + α I f ( x + ⌊ δ n , n − 1 ⌋ , n − 1 ) ,

где

[δ_n,n-1]=([δx_n,n-1],[δy_n,n-1])

соответствует вектору для сдвига x в ряду, и/или сдвига у в столбце, округленных до ближайших целых чисел, между текущим изображением n и предыдущим изображением n-1, вследствие поступательного перемещения камеры,

- для обновления матрицы N нормирования при:

N ( x , n ) = ( 1 − α ) × 1 + α N ( x + ⌊ δ n , n − 1 ⌋ , n − 1 )

- и для нормирования выхода временного фильтра, при:

I m ( x , n ) = 1 N ( x , n ) I f ( x , n )

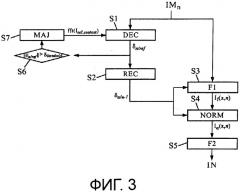
Настоящее изобретение также направлено на компьютерную программу, содержащую команды для реализации способа, представленного выше, когда эта программа выполняется с помощью процессора. Один пример блок-схемы последовательности операций общего алгоритма такой программы показан на фиг.3, которая будет подробно описана ниже.

Настоящее изобретение также направлено на устройство для обработки данных изображения, содержащее вход для обработки последовательных цифровых данных изображения, полученных камерой, погруженной в жидкость, содержащую явления турбулентности, вызывающие эффект видимого смещения пикселей изображений. В частности, такое устройство дополнительно содержит средство вычисления, предназначенное для реализации способа, представленного выше. Такое средство расчета может включать в себя процессор и рабочее средство хранения данных для выполнения, например, инструкций упомянутой выше компьютерной программы.

Настоящее изобретение, предпочтительно, применимо, но не ограничено этим, к обработке данных изображения, получаемых камерой, погруженной в воду в ядерных установках, для съемки сборок топливных элементов. Такое применение способа по изобретению, в этом контексте, может затем содержать по меньшей мере следующий этап:

- определяют на основе полученных и обработанных изображений состояние сборок топливных элементов.

Например, в полученных и обработанных изображениях может быть определен, по меньшей мере, один идентификатор сборки топливного элемента.

Вариант осуществления предпочтительно представляет компоновку сборок внутри активной зоны ядерного реактора, которую требуется отслеживать и проверять.

Применение способа, в смысле изобретения, может, кроме того, содержать этап, на котором:

- измеряют на упомянутых изображениях промежуток между сборками топливных элементов.

Такой вариант осуществления, предпочтительно, обеспечивает возможность точного отслеживания и проверки соответствующих положений сборок внутри активной зоны.

В конечном итоге, следует понимать, что осуществление способа настоящего изобретения в рамках такого применения позволяет выполнять общую инспекцию состояния сборок, как в воде резервуара реактора, так и в зале реактора или в бассейне выдержки топливного зала.

Настоящее изобретение также направлено на установку для реализации такого применения, содержащую по меньшей мере одну камеру, предпочтительно, водонепроницаемую и устойчивую к воздействию излучения, соединенную с устройством упомянутого выше типа для реализации изобретения.

Другие преимущества и свойства изобретения будут понятны при чтении подробного описания представленных ниже неограничительных примерных вариантов осуществления и также при просмотре приложенных чертежей, на которых:

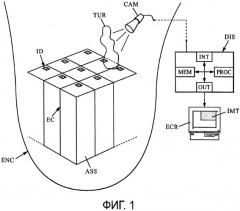
- на фиг.1 схематично показана зона реактора в рамках одной реализации в соответствии с изобретением, вместе с установкой, содержащей камеру и устройство для осуществления изобретения;

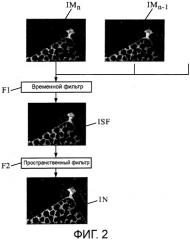
- на фиг.2 схематично показаны этапы способа в одном варианте осуществления изобретения, с поддержкой изображений, как необработанных, так и обработанных, с использованием варианта осуществления изобретения;

- на фиг.3 показана блок-схема последовательности операций этапов способа в одном варианте осуществления, где камера выполняет поступательное перемещение;

- на фиг.4 показано резкое изображение, полученное после использования способа, этапы которого представлены на фиг.3.

Прежде всего, будет сделана ссылка на фиг.1, на которой активная зона реактора в резервуаре ENC, заполненном водой, содержит множество сборок ASS ядерных топливных элементов (каждая из которых, например, обычно содержит множество топливных стержней). Каждая сборка ASS содержит идентификатор ID (окруженный белым кругом в виде на фиг.4), и сборки расположены через промежуток с использованием разделителей ЕС между сборками.

Затем предусмотрена камера САМ, которая снимает сборки ASS и, в частности, область, называемую "S отверстиями" между такими сборками (не показаны на фиг.1) и/или, по меньшей мере, один идентификатор ID сборки. Изображения, полученные с помощью камеры, затем позволяют:

- например, для S отверстий, идентифицировать деформацию отверстия в пределах времени использования, для уменьшения риска захвата сборок топливных узлов на штифтах, используемых для стабилизации сборок, и

- считывать идентификатор сборки для обеспечения того, что каждая сборка топливных элементов находится в местоположении, указанном в заданном плане активной зоны.

Такие изображения снимают с помощью камеры САМ, погруженной в воду, в которую погружены сборки. Вследствие разности температур в воде на месте (в результате локальных вариаций показателя преломления воды), может возникать явление TUR оптической турбулентности. Настоящее изобретение обеспечивает моделирование турбулентности, влияющей на изображение, и использует эту модель турбулентности, для обработки полученных изображений. Один предпочтительный вариант осуществления позволяет поступательно перемещать камеру, которая снимает эти изображения для обработки, в частности, используя технологию для смены положения изображения, которое адаптировано к скорости поступательного перемещения.

И снова, со ссылкой на фиг.1, камера САМ соединена с устройством DIS для обработки получаемых изображений, обычно содержащим:

- интерфейс INT, предназначенный для приема полученных данных изображения,

- процессор PROC и рабочий накопитель MEM для обработки этих данных изображения,

- выходной интерфейс OUT для предварительной обработки и передачи сигнала изображения на экран ECR, с последующим отображением обработанных изображений IMT (один пример обработанного изображения показан на фиг.4).

Таким образом, использование способа, в соответствии с данным изобретением, является предпочтительным в контексте дистанционной видеоинспекции, в частности, в конце перезагрузки топливных элементов, которая в настоящее время составляет важный этап при операциях остановки реактора для атомных электростанций, генерирующих электричество. Такие дистанционные видеоинспекции выполняются для проверки плана активной зоны (путем идентификации номеров сборок) и для точного определения местоположения этих сборок (например, путем измерения зазоров между сборками). Дистанционные видео инспекции, кроме того, например, позволяют проверять установку положения сборок.

Способ также предпочтительно применяться при обработке последовательности изображений (фотографий) для помощи, в частности, при расчете мест положения всех или части элементов сборок, но также и для инспекции состояния этих сборок, например, в топливном зале.

Интерпретация таких дистанционных видеоинспекций часто связана с трудностями, вследствие высвобождения тепла из топливных элементов, что вызывает явление турбулентности в воде. Для устранения таких трудностей была разработана технология для обработки снятых последовательностей изображения. Алгоритмы для такой обработки были разработаны для работы в режиме реального времени (следовательно, так, чтобы они позволяли обрабатывать непосредственно снимаемый поток видеоданных, кадр за кадром).

В глобальном смысле такая обработка основана на вероятностном моделировании воздействия турбулентности на пиксели изображений. Такая модель турбулентности позволяет определить алгоритм обработки восстановления на двух этапах:

- вначале временная фильтрация позволяет получить стабильное, но размытое изображение (было показано, что такое размытое изображение соответствует свертке исходного резкого изображения (неизвестно) с использованием линейного пространственного фильтра, выражение которого точно равно плотности вероятности вектора турбулентности);

- вторая фильтрация, которая выполняется пространственно, например, по типу Винера, позволяет сделать исходное изображение резким (которое, таким образом, получают, используя линейную обращенную свертку).

Обработка на этих двух этапах, описанных выше, применима, когда камера неподвижна. Из-за времени конвергенции временного фильтра, предпочтительно, обездвижить камеру на несколько секунд перед получением удовлетворительного восстановленного изображения. В одном предпочтительном варианте осуществления затем предусмотрена технология обработки изображений, когда камера движется (обычно в виде поступательного движения, соответствующего наиболее частому случаю).

В случае камеры, выполняющей поступательное движение, предусматривают этап (не обязательный, но предпочтительный) изменения положения изображения для того, чтобы обеспечить адаптацию временного фильтра к вариациям камеры. Такое изменение положения изображения выполняют путем предварительной оценки движения камеры. Рабочие характеристики являются удовлетворительными, предпочтительно, без потери качества относительно обработки с использованием статичной камеры.

Далее, в качестве первого этапа, будет описан один пример модели деградации, из-за турбулентности.

Ниже, I(x,n,c) обозначает значение пикселя с координатами x=(x,y) в n-том ряду полученного изображения, для компонента с (c=1, 2, 3, соответственно, для красного, зеленого, синего компонентов). Поскольку операции обработки идентичны для всех трех компонентов, обозначения упрощены так, что обрабатываемые компоненты не упоминаются, и I(x,n,c) просто записывают, как I(x,n).

В идеальных условиях (отсутствие турбулентности, статичная камера, постоянная сцена), изображения I(x,n), снимаемой последовательности кадров получают в результате выборки одного и того же резкого, оригинального и непрерывного изображения, обозначенного, как I_sharp(x), при I(x,n)=I_sharp(x).

Затем считается, что в присутствии турбулентности каждый пиксель изображения смещается от его исходного положения. Обозначая, как u_x,n, вектор, соответствующий сдвигу пикселя x на изображении n, может быть записано следующее:

I(x,n)=I_sharp(x+u_x,n)

Смещения, из-за турбулентности, кроме того, являются случайными. Поиск аналитического выражения для вектора u_x,n смещения, кажется чем-то, что не может быть представлено.

Затем предоставляют вероятностное описание этих смещений. Вектор u_x,n турбулентности рассматривают, как случайный вектор, в соответствии с определенной плотностью вероятности, обозначенной следующим образом:

h_x,n(u)

На основе предположения, что явления турбулентности являются стационарными, как по времени, так и в пространстве (в случае жидкой среды, такой как вода), можно рассматривать, что плотность вероятности не зависит ни от x, ни от n, и может быть записано следующее:

h_x,n(u)=h(u)

где h(u) представляет собой плотность вероятности турбулентности для любого заданного изображения n и для любого заданного пикселя x.

Представленные ниже операции обработки основаны на этой гипотезе стационарности явлений турбулентности. Реально, при обозначении, как I_m(x,n), усредненное изображение за время n определяется следующим образом:

I m ( x , n ) = 1 n ∑ k = 1 n I ( x , k ) ,

при этом было показано, что это усредненное изображение сходится в направлении стабильного изображения I_stable(x), которое равно свертке исходного резкого изображения (неизвестно) со следующей плотностью вероятности турбулентности:

I s t a b l e ( x ) = lim n → ∞ I m ( x , n ) = [ I s h a r p ⊗ h ] ( x )

Таким образом, для восстановления неизвестного резкого изображения, усредненное изображение должно быть подвергнуто только обращенной свертке по плотности вероятности турбулентности h(u). Поскольку такая плотность вероятности не известна, ниже представлена эмпирическая модель для описания вариаций плотности вероятности на основе двух следующих физических особенностей:

- явления турбулентности, в общем, являются изотропными, и плотность вероятности должна быть независимой от угла вектора u

- малые смещения пикселей проявляются более часто, чем значительные смещения пикселей: таким образом, когда норма вектора u уменьшается, значение h(u) должно уменьшиться.

Другие факторы, конечно, могут быть рассмотрены при выборе модели. Например, может быть практичным разместить аналитическое выражение, параметры которого регулируются для h(u), и, в частности, для его преобразования Фурье. Простая модель, которая проверяет все такие гипотезы, является моделью экспоненциально снижающегося типа, такой как, например:

h σ ( u ) = 3 π σ 2 exp { − 6 ‖ u ‖ σ }

В этой формуле σ представляет среднеквадратичное отклонение (среднее отклонение) нормы вектора турбулентности. Этот параметр позволяет учитывать различия уровня турбулентности, в соответствии со снятыми последовательностями кадров.

В качестве варианта, можно использовать Гауссову модель. Однако, тесты с экспоненциальной моделью показали хорошие результаты. Другие типы моделей, проявляющие меньшее снижение, чем Гауссово, или экспоненциальные модели, конечно, могут быть рассмотрены, как дополнительные варианты.

Затем возможно выполнить оценку оригинального изображения на двух этапах обработки. На первом этапе, последовательность необработанных изображений усредняют по времени. Такое усредненное изображение сходится к стабильному изображению I_stable(x), которое равно свертке неизвестного резкого изображения (которое могло бы наблюдаться при отсутствии явлений турбулентности) с плотностью вероятности турбулентности, при:

I s t a b l e ( x ) = lim n → ∞ I m ( x , n ) = [ I s h a r p ⊗ h ] ( x )

Обращенная свертка усредненного изображения по плотности вероятности турбулентности затем, на втором этапе, позволяет выполнить оценку оригинального резкого изображения.

На фиг.2 иллюстрируются два основных этапа обработки реальных изображений сборок. Первый (временной) фильтр F1 позволяет получить усредненное, стабильное, но размытое изображение ISF, начиная с последовательности изображений IM_n, IM_n-1 и т.д.

Второй (обращенной пространственной свертки) фильтр F2, позволяет восстановить исходное резкое изображение IN, начиная с размытого изображения ISF.

Временная фильтрация F1 будет описана ниже.

Если снятая сцена является постоянной (игнорируя эффекты турбулентности), в частности, в том, что касается освещения, коэффициента увеличения и т.д., n-тое усредненное изображение получают по следующей формуле:

I m ( x , n ) = 1 n ∑ k = 1 n I ( x , k )

В этой формуле один и тот же вес назначают для каждого изображения. Для обработки любых потенциальных вариаций сцены (освещения и других), предпочтительно назначать, для усредненного изображения, больший вес для последних изображений, чем для прошлых изображений. Для среднего изображения в момент времени n, изображение I_α(x,n) снимают на основе следующего:

I α ( x , n ) = 1 − α 1 − α n ∑ k = 0 n − 1 α k I ( x , n − k )

Член α представляет собой фактор забывания, который позволяет назначать большую или меньшую степень важности для прошлых изображений (как память предыстории фильтра). Нормализация по члену

1 − α 1 − α n

позволяет получить геометрическую сумму весов α^k, равную 1, поскольку:

1 − α 1 − α n ∑ k = 0 n − 1 α k = 1

Формула I_α(x,n) может принимать форму рекурсивной временной фильтрации, после которой следует этап нормализации. N-тый выход временного фильтра, обозначенный, как I(x,n), и нормализованного выходного изображения, обозначенного, как I_α(x,n), затем связывают следующим:

I f ( x , n ) = α I f ( x , n − 1 ) + ( 1 − α ) I ( x , n )

I α ( x , n ) = 1 1 − α n I f ( x , n )

Значение, выбранное для фактора α забывания, определяет рабочие характеристики временного фильтра. Для оценки таких рабочих характеристик, определяют среднюю квадратичную разность между пикселем x n-ого изображения и пикселем x целевого стабильного изображения следующим образом:

Г α 2 ( x , n ) = E { ( I α ( x , n ) − I s t a b l e ( x ) ) 2 }

Затем возможно определить среднеквадратичную разность для всего изображения n:

Г α 2 ( n ) = 1 N p i x e l s ∑ x Г α 2 ( x , n )

В случае постоянной сцены, игнорируя эффекты турбулентности, было показано следующее:

Г α 2 ( n ) = ( 1 − α 2 n ) ( 1 − α ) ( 1 − α n ) 2 ( 1 + α ) ∑ 2

где Σ² представляет собой среднее отклонение пикселей n в необработанном изображении. После конвергенции (когда n стремится к бесконечности), остаточная квадратичная разность нормализованного выхода временного фильтра определяется следующим образом:

Г α 2 ( ∞ ) = ( 1 − α 1 + α ) ∑ 2

Расчеты свертки среднеквадратичного отклонения, как функции количества обработанных изображений, для различных значений фактора α забывания, показывают, что в случае статической сцены, предпочтительно, выбрать α, как можно большим. Однако, в случае переменной сцены, выбор фактора α забывания выполняют на основе компромисса между коротким временем для адаптации к изменению сцены (малое значение α) и малым остаточным среднеквадратичным отклонением (большое значение α). Если, например, возникает резкое изменение сцены (например, изменение освещения) в момент времени n₀, в то время как для временного фильтра было выполнено схождение, было показано, что среднеквадратичное отклонение между выходом фильтра в момент времени n и стабильным изображением становится:

Г α 2 ( n ) = ( 1 − α 1 + α ) ∑ 2 + α 2 ( n − n 0 ) Δ 2

где Δ представляет среднее отклонение уровня, вызванное изменением сцены.

Таким образом, чем больше значение фактора α забывания, тем большее время конвергенции будет получено (приблизительно 300 изображений или 12 секунд для α=0,99), но остаточное среднеквадратичное отклонение при этом является достаточно малым (0,07 для α=0,99) для выходного изображения, которое должно обладать возможностью стабилизации. При уменьшении выбранного значения α повышается скорость схождения (приблизительно 50 изображений, или 2 секунды, для α=0,95), но остаточное среднеквадратичное отклонение также увеличивается (0,16 для α=0,95). Выходное изображение не будет полностью стабилизировано, даже после схождения.

В одном текущем варианте осуществления фактор забывания, предпочтительно, установлен, как 0,99, что представляет собой оптимальное значение, в случае постоянной сцены (игнорируя эффекты турбулентности). Однако, представленная здесь обработка, является достаточно гибкой для адаптации к частым изменениям снимаемой сцены (обычно изменению освещения).

В частности, в случае движущейся камеры (представленной ниже), каждый элемент сцены является видимым только на уменьшенном количестве изображений. При этом предпочтительно уменьшить фактор забывания для того, чтобы назначить большую значимость для времени конвергенции, чем для остаточного расхождения.

Пространственная фильтрация, используемая на втором этапе способа, будет описана ниже в одном примерном варианте осуществления.

В соответствии с моделью деградации, описанной выше, нормализованный выход, I_α(x,n) становится равным стабильному изображению I_stable(x) (свертка неизвестного резкого изображения с плотностью вероятности, соответствующей турбулентности), для которого добавляют шум b(x,n) со средн