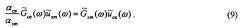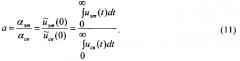Способ учета влияния нестабильности излучения лазера при воспроизведении и передаче единицы мощности

Способ учета влияния нестабильности излучения лазера при воспроизведении и передаче единицы мощности

Иллюстрации

Показать все

Реферат

Изобретение относится к технике фотометрии и радиометрии и предназначено для повышения точности воспроизведения и передачи единицы средней мощности лазерного излучения в условиях нестабильного лазерного излучения.

Известен способ учета влияния нестабильности мощности лазерного излучения на конечный результат воспроизведения единицы средней мощности лазерного излучения и передачи ее размера [1]. Способ основан на алгоритме восстановления формы непрерывного лазерного излучения, поступавшего на вход измерительной системы эталона единицы средней мощности лазерного излучения. При измерениях по показаниям эталонного измерительного преобразователя вычисляются параметры модельной импульсной функции, состоящей из двух экспонент. Одновременно со снятием сигналов с эталонного измерительного преобразователя снимаются показания с приемника-свидетеля, постоянная времени которого много меньше постоянной времени эталонного измерительного преобразователя. Далее по дискретным показаниям приемника-свидетеля вычисляются составляющие нестабильности мощности лазерного излучения, такие как дрейф мощности, скачок и флуктуации. Затем вычисляется интегральный поправочный коэффициент, который позволяет скорректировать измеряемую мощность с учетом указанных нестабильностей лазерного излучения.

Недостатком этого способа являются: использование модельной импульсной функции и ограниченность применимости метода малыми флуктуациями мощности лазерного излучения, до 5% от среднего уровня.

Известен способ учета нестабильности излучения лазера [2], являющийся наиболее близким к описываемому способу. Способ реализован в алгоритме обработки показаний средств измерений при передаче единицы средней мощности лазерного излучения с целью снижения влияния флуктуации мощности используемого лазера.

Основным результатом работы алгоритма является определение коэффициента передачи a единицы измерений от приемника с большой постоянной времени приемнику с малой постоянной времени. Коэффициент передачи a является отношением сигнала приемника с большой постоянной времени u_эт(t) к сигналу приемника с малой постоянной времени u_св(t) в условиях стабильной мощности лазерного излучения. В свою очередь, данные сигналы можно представить в виде:

где i - соответствует индексам «эт» или «св» от слов «эталон» и «свидетель» соответственно, P_опт(t) - оптическая мощность лазерного излучения, G_i(t) - импульсные функции соответствующих приемников, α_i - коэффициенты преобразования соответствующих приемников. При этом предполагается, что импульсные функции приемников G_i(t) модельно можно представить в виде:

где τ_i - постоянная времени соответствующего измерительного преобразователя. Для снижения влияния флуктуации мощности лазерного излучения при вычислении a вместо величин u_i(t) необходимо использовать величины α_i·P_опт(t) из (1). Для импульсных характеристик вида (2) операцию обратной свертки, выражающую из (1), можно представить в виде:

Переходя от уравнения (3) к дискретным во времени величинам u_i(t), получим:

где - интегральное среднее значение u_i(t) на интервале времени от t-T до T. С использованием значений и вычисляется коэффициент передачи a единицы измерений от приемника с большой постоянной времени приемнику с малой постоянной времени. Было установлено, что при использовании параметра T≈τ_эт и шага дискретизации (0,1÷0,4)τ_св, для скачкообразного изменения величины P_опт(t) в ε раз относительная погрешность определения величины a сокращается более чем на порядок по сравнению с величиной .

Рассматриваемый метод был разработан специально для флуктуации мощности лазерного излучения вида скачков амплитуды мощности. В реальности при плавных флуктуациях величины u_св(t) относительная погрешность определения величины а сокращается не более чем в 6÷7 раз.

Основной недостаток предложенного способа, ограничивающий его применение малыми флуктуациями мощности лазерного излучения, заключается в использовании модельного вида импульсных функций приемников (2), а также использовании полученной из (2) и ограниченной в своем применении формулы (4).

Техническая задача, решаемая заявляемым изобретением, состоит в том, чтобы повысить точность воспроизведения и передачи единицы средней мощности лазерного излучения в условиях нестабильного лазерного излучения.

Решение данной задачи достигается за счет использования реально измеренной импульсной функции измерительного преобразователя с большой постоянной времени, позволяющей с высокой точностью определять коэффициент передачи единицы средней мощности от измерительного преобразователя с большой постоянной времени измерительному преобразователю при существенной нестабильности лазерного излучения.

Таким образом, последовательность действий при реализации предлагаемого способа состоит в следующем: в процессе воспроизведения единицы мощности лазерного излучения используются два измерительных преобразователя, с которых снимаются в ограниченный промежуток времени выходные сигналы при подаче оптической мощности лазерного излучения; и способ отличается тем, что используются измерительные преобразователи с отличающейся постоянной времени не менее чем на два порядка; по экспериментальным данным определяются импульсные функции измерительных преобразователей; вычисляется свертка сигнала с измерительного преобразователя с меньшей постоянной времени с импульсной функцией измерительного преобразователя с большей постоянной времени; вычисляется коэффициент пропорциональности между функцией измерительного преобразователя с большей постоянной времени и результатом полученной свертки; вычисленный коэффициент пропорциональности является коэффициентом передачи единицы средней мощности для данной геометрии эксперимента и данного измерительного преобразователя с меньшей постоянной времени.

В основу предлагаемого способа положен последовательный метод передачи единицы средней мощности лазерного излучения от измерительного преобразователя с большой постоянной времени к поверяемому измерительному преобразователю. Обозначим измерительный преобразователь с большой постоянной времени, как эталонный измерительный преобразователь ЭИП. Метод может использоваться в том случае, когда характерное время установления теплового равновесия в поверяемом измерительном преобразователе (приемнике) значительно меньше постоянной времени измерительного преобразователя τ_эт. Процедура состоит из двух этапов. Вначале определяется коэффициент передачи единицы мощности лазерного излучения от ЭИП приемнику-свидетелю, который представляет собой либо фотоэлектрический приемник, либо тепловой приемник. Затем на место ЭИП в той же оптической схеме помещают поверяемый приемник. Процедура измерения повторяется. В результате мощность на поверяемом приемнике выражается через полученные из этих двух экспериментов коэффициентов передачи единицы мощности приемнику-свидетелю и, в конечном счете, через мощность на ЭИП. Абсолютная величина единицы мощности лазерного излучения приемнику-свидетелю в процессе этих измерений не передается. В процессе передачи единицы средней мощности используются только относительные измерения приемника-свидетеля.

На каждом этапе в процессе таких измерений участвуют два приемника. Мы рассмотрим первую пару: ЭИП - приемник-свидетель, полагая, что полученные результаты будет несложно обобщить на вторую пару: приемник-свидетель - поверяемый приемник. Поскольку нас интересуют временные зависимости, обусловленные в чистом виде изменением мощности лазерного излучения, то при использовании тепловых приемников их сигнал обязательно должен быть скорректирован с учетом дрейфа их нуля.

Сигналы от первых двух приемников можно представить в виде

где P(t) - мощность излучения на выходе из лазера, G_эт(t) и G_св(t) - импульсные функции ЭИП и приемника-свидетеля, α_эт и α_св - размерные коэффициенты, характеризующие долю поглощенной мощности соответствующими приемниками.

Выражая из уравнений (5) и (6) P(t) и приравнивая результаты, получаем

Из уравнения (7) несложно получить

Применяя к уравнению (8) преобразование Фурье имеем

Выражая из (9) и используя обратное преобразование Фурье, для величины G_св(t) получаем

Интегрируем затем обе стороны уравнения (10) по t в пределах от 0 до ∞ и, учитывая нормировку импульсной функции, , получаем

Величина a представляет собой коэффициент передачи единицы средней мощности от ЭИП приемнику-свидетелю.

При использовании быстрого приемника-свидетеля с τ_св<<τ_эт можно получить отличное от (11) приближенное решение задачи. Основой этого приближения является предположение о том, что импульсную функцию приемника-свидетеля можно заменить на дельта-функцию Дирака, т.е. приемник-свидетель регистрирует временной профиль мощности падающего лазерного излучения. Далее вычисляется импульсная функция ЭИП. На Фиг.1 показан пример сигнала U(t), измеренного ЭИП при высокостабильном источнике излучения (лазер Coherent Verdi V8).

Для получения импульсной функции ЭИП идеальным представляется участок измерений u_спад на интервале [t₂, t₃] (см. Фиг.1), поскольку на нем отсутствует влияние нестабильности лазера и других внешних факторов. Импульсная функция вычисляется по следующей формуле:

Чтобы импульсная функция не искажала абсолютного значения сигнала, ее необходимо нормировать. В дальнейшем под G_эт(t) будем понимать нормированную импульсную функцию.

Для более точного определения импульсной функции необходимо вычислить усредненную импульсную функцию по множеству измерений, подобных показанному на Фиг.1.

Следующий шаг заключается в вычислении сигнала ЭИП с помощью свертки полученной импульсной функции и сигнала приемника-свидетеля. Согласно сделанному выше упрощению

где коэффициент a определяется по методу наименьших квадратов минимизацией следующего функционала:

Результат процедуры минимизации можно представить в виде:

Следует отметить, что проведенное выше рассмотрение базируется на предположении о линейности по температуре показаний термопар обоих приемников. В первом приближении такой подход обоснован как вследствие малого интервала температур нагрева приемников, так и слабой нелинейности самого эффекта [3].

Для проверки эффективности предлагаемого способа использовался рассматриваемый последовательный метод передачи единицы мощности от ЭИП через приемник-свидетель поверяемому приемнику, в качестве которого выступал тот же ЭИП. Как показали результаты измерений с использованием фотоэлектрического приемника-свидетеля, при нестабильности мощности лазерного излучения ~10% относительное отличие передаваемого единицы мощности лазерного излучения от исходной составило 0,003%. А при использовании теплового приемника-свидетеля - 0,03%. Проведение аналогичной процедуры с использованием «классического» метода или корректирующего алгоритма [1] приводит к погрешностям порядка процентов.

Таким образом, предложен способ, основанный на использовании реально измеренной импульсной функции эталонного приемника, позволяющий с высокой точностью определять коэффициент передачи единицы средней мощности от эталонного приемника приемнику-свидетелю при существенной нестабильности лазерного излучения.

Способ найдет широкое применение в лазерной радиометрии и фотометрии в эталонах единицы средней мощности лазерного излучения различных разрядов при воспроизведении и передаче единицы мощности нижестоящим эталонам и средствам измерений.

Литература

1. А.А. Ковалев, А.А. Либерман, С.А. Москалюк. Учет влияния нестабильности мощности лазерного излучения на конечный результат воспроизведения единицы средней мощности лазерного излучения и передачи ее размера // Измерительная техника, 2004, №8, с.55-57.

2. Костин А.А., Либерман А.А., Медик B.C. Оптимизированный алгоритм обработки результатов измерений при воспроизведении и передаче размера единицы СМЛИ. // Метрология. 2002. №1. С.30-39.

3. Таблицы физических величин: Справочник / под ред. Кикоина И.К. М.: Атомиздат, 1976. С.96.

Способ учета влияния нестабильности излучения лазера при воспроизведении и передаче единицы мощности, заключающийся в том, что в процессе воспроизведения единицы мощности лазерного излучения используют два измерительных преобразователя, с которых снимают в ограниченный промежуток времени выходные сигналы при подаче оптической мощности лазерного излучения;и отличающийся тем, чтоиспользуют измерительные преобразователи с отличающейся постоянной времени не менее чем на два порядка;по экспериментальным данным определяют импульсные функции измерительных преобразователей;вычисляют свертку сигнала с измерительного преобразователя с меньшей постоянной времени с импульсной функцией измерительного преобразователя с большей постоянной времени;вычисляют коэффициент пропорциональности между функцией измерительного преобразователя с большей постоянной времени и результатом полученной свертки;за коэффициент передачи единицы средней мощности принимают вычисленный коэффициент пропорциональности для данной геометрии эксперимента и данного измерительного преобразователя с меньшей постоянной времени.