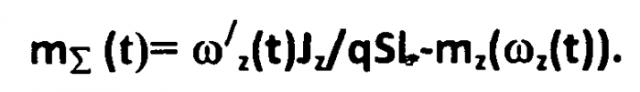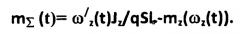Способ непараметрической идентификации нелинейных аэродинамических характеристик летательного аппарата по результатам лётных исследований

Способ непараметрической идентификации нелинейных аэродинамических характеристик летательного аппарата по результатам лётных исследований

Иллюстрации

Показать все

Реферат

Изобретение относится к областям авиакосмической и авиационной техники, а именно к способам идентификации аэродинамических характеристик (АДХ) летательного аппарата при проведении летных исследований:

- зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угла отклонения руля высоты,

- зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угловой скорости тангажа,

- зависимости коэффициента подъемной силы от угла атаки и зависимости коэффициента подъемной силы от угла отклонения руля высоты.

Отличительная особенность предлагаемого способа идентификации указанных аэродинамических характеристик заключается в том, что идентификация производится на относительно простом тестовом сигнале и без каких-либо априорных предположений относительно характера нелинейности идентифицируемых однозначных аэродинамических характеристик.

Исключение ошибок априорных предположений о характере нелинейностей идентифицируемых зависимостей обеспечивает повышение достоверности определения при летных испытаниях нелинейных аэродинамических характеристик предлагаемым способом, позволяет сократить сроки и повысить эффективность летных испытаний.

Область применения предлагаемого способа идентификации определяется условием, что каждая из идентифицируемых зависимостей в области определения является однозначной функцией своего аргумента (т.е. угла атаки или угла отклонения руля высоты, или угловой скорости тангажа), а сами эти зависимости являются аддитивными составляющими зависимости коэффициента аэродинамического момента тангажа, или зависимости коэффициента подъемной силы от указанных аргументов,

В практике летных испытаний широко применяются способы идентификации параметров математических моделей движения летательных аппаратов (см. метод наименьших квадратов, методы, основанные на использовании настраиваемых моделей, адаптивные алгоритмы идентификации в книге В.А. Касьянов, Е.П. Ударцев «Определение характеристик воздушных судов методами идентификации». М.: Машиностроение, 1988 г.) - методы параметрической идентификации. Применение этих методов основано на аппроксимации или постулировании структуры зависимостей коэффициентов аэродинамических сил или аэродинамического момента (далее - просто «коэффициентов») от параметров полета. При этом выбор структуры той или иной зависимости определяется или интуицией исследователя, или данными априорных трубных испытаний, что может приводить к значительным ошибкам результата идентификации, поскольку известно (см. монографию Е.З. Демиденко «Линейная и нелинейная регрессия». М.: Финансы и статистика, 1984), что даже в относительно простом случае идентификации параметров линейной регрессии, широко используемым на практике методом наименьших квадратов, «перебор» в структуре модели приводит к потере точности результата, а «недобор» -дополнительно еще и к систематическим ошибкам в результате.

Известен «Способ определения АДХ воздушных судов», пат. №2460982 от 28.03.2011.

В пат. №2460982 от 28.03.2011 предлагается при проведении послеполетной идентификации АДХ предположить, что структуры зависимостей коэффициентов от параметров полета в основном верно определены в априорных трубных исследованиях, и требуется по результатам летных исследований лишь уточнить методом наименьших квадратов «коэффициенты влияния» отдельных, или всех составляющих этой структуры. Данный подход является способом параметрической идентификации и основным его недостатком является предположение о том, что структуры зависимостей коэффициентов от параметров полета определены в наземных стендовых исследованиях качественно верны. Однако летный эксперимент проводится для проверки априорных трубных оценок, и хорошо известно, что результаты летных исследований - особенно при освоении новых режимов полета - могут качественно отличаться от априорного прогноза.

Известен «Способ идентификации АДХ летательного аппарата по результатам испытаний», пат. №2419775 от 28.12.2009.

В пат. №2419775 от 28.12.2009 способ идентификации АДХ на скользящем интервале переменной - настраиваемой - длины также является способом параметрической идентификации. При этом структура зависимости коэффициента задается априори, а использование скользящего интервала призвано учитывать возможное изменение параметров математической модели при изменении режимов полета. Основной недостаток данного подхода в постулировании структуры математической модели и использовании экспертных оценок при выборе длины скользящего интервала.

При практической идентификации АДХ по результатам летных испытаний широкое распространение получил непараметрический способ восстановления характеристик - «метод сечений», изложенный в книге Снешко Ю.И. Исследования в полете устойчивости и управляемости самолета. М.: Машиностроение, 1971, как способ восстановления аддитивных составляющих аэродинамического момента по измерениям (оценкам) суммарного момента, угла отклонения руля высоты и угла атаки методом сечений. При его применении исходят из того, что задача идентификации нередко может быть упрощена за счет привлечения априорных данных и редуцирована к задаче идентификации двух наиболее нелинейных характеристик.

В данном способе искомые характеристики получаются путем выделения из всей совокупности измерений тех измерений, которые соответствуют фиксированному значению одного из двух аргументов (сечению). Таким образом, в сечении зависимость коэффициента момента от другого аргумента представляет - с точностью до константы - искомую зависимость. Строя сечения по второму аргументу, получаем - с точностью до константы - искомую зависимость от первого аргумента.

Результат использования метода сечений - совокупность сечений, соответствующих разным фиксированным значениям аргументов, каждое сечение содержит несколько экспериментальных точек (в каждом сечении разных) - значений искомых составляющих с точностью до константы, зависящей от сечения.

Главный недостаток метода сечений - неполнота восстановления составляющих - каждое сечение может содержать слишком мало точек, чтобы по ним можно было судить о виде нелинейности. Например, если движение летательного аппарата удовлетворительно описывается линейной моделью короткопериодического продольного движения, то в случае гармонического входного воздействия (отклонения руля высоты по гармоническому закону) зависимость в установившемся движении представляет собой эллипс. Следовательно, каждое сечение будет содержать всего две точки, что, очевидно, недостаточно для описания нелинейной функции.

«О некоторых методах идентификации нелинейных объектов» авторами Самсоновым В.В., Сильвестровым A.M. (Aninternational jornal "Mathematics and Computer Science", Jornal of Qafqaz University. - 2011, №32 c 12-23) предложены несколько подходов к идентификации нелинейных объектов, в том числе к непараметрическому оцениванию нелинейного входного воздействия в модели Гаммерштейна и к восстановлению полной нелинейной модели по частным моделям.

Суть первого подхода состоит в параметрической идентификации коэффициентов дифференциальной модели динамики объекта с неизвестной нелинейной функцией от входного воздействия из условия гладкости указанной функции. Указанная функция находится в результате минимизации по искомым коэффициентам определенного функционала с параметром, характеризующим гладкость указанной функции, при дополнительном предположении о независимости некоторых производных выходного сигнала.

В отличие от данного подхода предлагаемый подход не предполагает параметризацию модели уравнения динамики объекта, в нем не делается предположений о независимости некоторых производных выходного сигнала, а восстановление нелинейных функций производится в результате относительно простого итерационного процесса, не связанного с минимизацией функционала.

В другом подходе, предложенном в статье «О некоторых методах идентификации нелинейных объектов» авторов Самсонова В.В., Сильвестрова A.M. (An International jornal "Mathematics and Computer Science", Jornal of Qafqaz University. - 2011, №32 с 12-23), для восстановления полной нелинейной модели, зависящей от нескольких переменных (приведены примеры моделей от двух и трех переменных), как и в предлагаемом способе, используется метод сечений. Однако данный метод используется для построения так называемых частных моделей, т.е моделей, зависящих только от одного переменного, каждая из которых описывает поведение полной модели в том или ином «сечении», т.е. при фиксированных значениях остальных переменных. При этом структура частной моделей постулируется (она одна и та же для всех сечений), а определение неизвестных коэффициентов частных моделей (для каждого сечения в отдельности) производится методом параметрической идентификации (методом наименьших квадратов). Далее сами найденные таким образом коэффициенты объявляются зависящими от другой переменной, причем структура этой зависимости также постулируется, а неизвестные коэффициенты снова находятся методом наименьших квадратов и т.д.

Как следует из описания, основным отличием данного подхода от предлагаемого является использование частных моделей заданной структуры с неизвестными коэффициентами, для определения которых используется способ параметрической идентификации. Существенное различие подходов наглядно проявляется в практически важном случае, когда полная модель представляет собой сумму двух нелинейных функций, каждая из которых однозначно зависит от своего переменного, и эти переменные изменяются по гармоническому закону так, что зависимость одной переменной от другой представляет собой эллипс (см. фиг. 1). В этом случае каждое из сечений содержит только две точки. Следовательно, и частная модель может содержать не более двух коэффициентов, что заведомо недостаточно для описания нелинейной функции в общем случае. При этих же условиях предлагаемый способ способен восстановить обе нелинейные функции любого вида.

Наиболее близким к предлагаемому способу является «Способ идентификации аэродинамических характеристик автоматически управляемых летательных аппаратов по результатам испытаний», пат. №2124711 от 05.09.1994 г., который предназначен для последовательной идентификации аэродинамических характеристик произвольного вида. Применительно к задаче идентификации составляющих момента тангажа от угла атаки и угла отклонения руля высоты способ заключается:

- в воздействии на привод руля высоты низко- и высокочастотными гармоническими составляющими одновременно. В подаче на руль высоты двухчастотного тест-сигнала. Высокая частота и амплитуда гармоники подбираются таким образом, чтобы амплитуда колебаний угла атаки на данной частоте была много меньше амплитуды колебания угловой скорости на этой же частоте. Низкая частота и амплитуда соответствующей гармоники подбираются исходя из желаемого диапазона изменения угла атаки (и, соответственно, диапазона определения АДХ по углу атаки);

- по результатам измерения в полете угловой скорости, оценок скоростного напора и моментов инерции определяется коэффициент момента тангажа. Предполагается, что величина коэффициента момента тангажа определяется в основном двумя составляющими: составляющей от угла атаки и составляющей от угла отклонения руля высоты, вклад демпфирующей составляющей невелик и поэтому с незначительной относительной погрешностью может быть учтен по данным продувок. Таким образом, задача идентификации сводится к задаче оценки только двух составляющих: от угла атаки и от угла отклонения руля высоты, которые идентифицируются последовательно;

- на каждом периоде высокочастотного движения незначительное изменение коэффициента момента от угла атаки учитывают - с небольшой относительной погрешностью - по данным продувок. Оставшееся изменение коэффициента момента на данном периоде есть только составляющая от угла отклонения руля высоты, что позволяет оценить эффективность руля высоты - при текущем на периоде угле атаки - как отношение диапазона изменения коэффициента момента к диапазону изменения руля высоты;

- оценка составляющей от угла атаки определяется на периоде низкочастотного движения по коэффициенту момента тангажа и полученной в п. 3 оценке эффективности руля высоты.

Недостатками данного способа являются априорная потребность в достаточно подробной математической модели аэродинамики летательного аппарата, позволяющей выбрать необходимые частоты и амплитуды тестового сигнала, и необходимость в наличии привода руля высоты с высокими характеристиками быстродействия, необходимыми для формирования настолько высокой частоты изменения угла отклонения руля высоты, что она не отражается на изменении угла атаки. Сложная форма тест-сигнала требует для его реализации на борту ЛА наличия БЦВМ или специального устройства…

Технический результат, на достижение которого направлено предлагаемое изобретение, заключается в повышении достоверности и технологичности определения по результатам летных испытаний нелинейных аэродинамических характеристик, так как при использовании предлагаемого способа идентификации, в отличие от методов параметрической идентификации:

- не требуются дополнительные априорные предположения о характере нелинейностей и априорной аппроксимации этих нелинейностей;

- каждая из искомых зависимостей восстанавливается в виде единой совокупности точек, которая отображает - с точностью до константы - соответствующую составляющую во всем диапазоне изменения ее аргумента;

- не требуется применение тестового сигнала сложной формы и соответствующей аппаратуры на борту ЛА для его воспроизведения, позволяет определить момент демпфирования ЛА, не предъявляет повышенных требований к быстродействию привода руля высоты ЛА, необходимого для формирования настолько высокой частоты изменения угла отклонения руля высоты, что она не отражается на изменении угла атаки.

Для достижения названного технического результата в предлагаемом способе непараметрической идентификации по результатам летных исследований двух нелинейных аэродинамических характеристик: зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угла отклонения руля высоты или зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угловой скорости тангажа, или зависимости коэффициента подъемной силы от угла атаки и зависимости коэффициента подъемной силы от угла отклонения руля высоты, включающего подачу на привод руля высоты летательного аппарата тестового сигнала, возмущение движения летательного аппарата, измерение параметров движения летательного аппарата, обработку измерений (с привлечением при необходимости априорных данных об иных аэродинамических характеристиках, кроме идентифицируемых) для получения аргументов идентифицируемых зависимостей (угла атаки и угла отклонения руля высоты или угла атаки и угловой скорости тангажа), а также зависимости коэффициента аэродинамического момента тангажа, или зависимости коэффициента подъемной силы от указанных аргументов,

- подают на привод руля высоты летательного аппарата тестовый сигнал, обеспечивающий колебательный характер изменения по времени аргументов идентифицируемых зависимостей на исследовательском режиме полета летательного аппарата таким образом, чтобы диапазоны изменений аргументов идентифицируемых зависимостей были не менее диапазонов, для которых требуется идентифицировать зависимости, а фазовая траектория (то есть зависимость одного аргумента от другого аргумента) была бы замкнутой;

- проводят измерение параметров возмущенного движения летательного аппарата,

- проводят обработку измерений (с привлечением при необходимости априорных данных об иных аэродинамических характеристиках, кроме идентифицируемых) для получения трех функций времени: двух аргументов идентифицируемых зависимостей и суммы идентифицируемых зависимостей;

- строят последовательность сечений фазовой траектории поочередно по каждому из аргументов таким образом, чтобы в двух последовательных сечениях содержалась как минимум одна и та же точка фазовой траектории, последовательно объединяют - используя общие точки в последовательных сечениях - все точки всех построенных сечений в две совокупности, каждая из которых представляет собой - с точностью до константы - поточечное представление искомой идентифицируемой зависимости от своего аргумента, например зависимости коэффициента аэродинамического момента тангажа от угла атаки, или зависимости коэффициента аэродинамического момента тангажа от угла отклонения руля высоты.

Таким образом, искомые аэродинамические характеристики идентифицируются с использованием относительно простого тестового сигнала, без предположений о характере нелинейностей и априорной аппроксимации этих нелинейностей, чем и достигается повышение достоверности и технологичности определения по результатам летных испытаний нелинейных аэродинамических характеристик.

Предлагаемый способ поясняется на фиг. 1 -5:

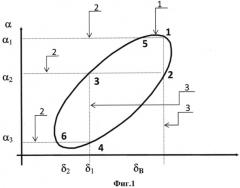
на фиг. 1 изображена схема фазовой траектории и способа построения сечений;

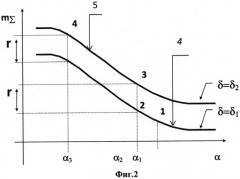
на фиг. 2 изображена схема зависимости коэффициента момента тангажа ЛА от угла атаки в двух сечениях по углу отклонения руля высоты, соответствующих фиг. 1;

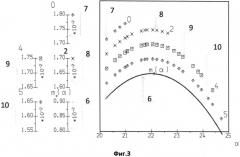
на фиг. 3 показана зависимость коэффициента момента тангажа ЛА от угла атаки и результаты ее идентификации после нулевой (метод сечений), второй, четвертой и пятой итераций;

на фиг. 4 показана зависимость коэффициента момента тангажа ЛА от угла отклонения руля высоты и результаты ее идентификации после нулевой (метод сечений), второй и четвертой итераций;

на фиг. 5 приведена фазовая траектория - зависимость угла атаки от угла отклонения руля высоты.

Способ осуществляется следующим образом.

1. Для идентификации зависимости коэффициента момента тангажа ЛА от угла отклонения руля высоты m_z(δ_в) и зависимости коэффициента момента тангажа ЛА от угла атаки m_z(α) способ реализуется следующим образом.

На привод руля высоты подается тестовый сигнал, удовлетворяющий двум требованиям: диапазоны изменения аргументов угла атаки α и угла отклонения руля высоты δ_в не меньше диапазонов, в которых требуется восстановить зависимости m_z(α) и m_z(δ_в), каждое сечение зависимости α(δ_в) прямой δ в = δ в 0 = c o n s t (прямой α=α⁰=const), где значение δ в 0 (значение α⁰), принадлежит требуемому диапазону определения зависимости m_z(δ_в)(m_z(α)), содержит не менее двух точек (см. Фиг. 1), позиция 1 - зависимость α(δ_в), моделирующая наихудший для идентификации методом сечений случай, когда зависимость α(δ_в) при колебательном режиме полета ЛА представляет собой эллипс, а каждое сечение содержит, соответственно, всего две точки. Пунктиром указаны сечения данной зависимости, соответствующие трем фиксированным значениям α (позиция 2) и двум фиксированным значениям δ_в (позиция 3). Цифрами обозначены номера точек, содержащихся в указанных сечениях. Данным требованиям к тестовому сигналу удовлетворяет, например, гармонический сигнал необходимой амплитуды.

На данном режиме полета производятся измерения параметров полета ЛА в соответствующем канале: угловой скорости, угла атаки, угла отклонения руля высоты, скоростного напора. Выполняется цифровое сглаживание измерений и дифференцирование угловой скорости.

По данным измерениям определяется коэффициент момента тангажа m_z(t) как функция времени полета t.

Влияние на коэффициент m_z(t) всех параметров полета - за исключением параметров α и δ_в - учитывается по априорным данным. Таким образом, по известному коэффициенту момента тангажа и априорным данным определяется сумма двух наиболее значимых составляющих

m_z∑(t)=m_z(α(t))+m_z(δ_в(t)) как функция времени полета.

По трем известным временным зависимостям: углу атаки α(t), углу отклонения руля высоты δ_в(t) и сумме составляющих коэффициента момента тангажа m_∑(t)=m_z(α(t))+m_z(δ_в(t)) производится идентификация зависимостей m_z(α) и m_z(δ_в):

- Проводится сечение δ_в=δ₁, где δ₁ - произвольное значение угла отклонения руля высоты на режиме обработки. Это сечение состоит (см. Фиг. 1) из точек 1(α₁,δ₁), 2(α₂,δ₂). При построении сечений используется интерполяция временных зависимостей α(t), δ_в(t), (t) между точками измерений.

- Значение δ_в=δ₂, определяющее второе сечение, находится следующим образом. Возьмем одну из точек 1-го сечения, например точку 2, и проведем вспомогательное сечение по α, которое, помимо точки 2, содержит новую точку 3(α₂, δ₂). Проведем сечение δ_в=δ₂. Этому сечению помимо точки 3 принадлежит точка 4(α₃, δ₂).

- Осуществим приведение точек второго сечения к первому сечению. Выпишем значения моментов в соответствующих точках (см. Фиг. 2) - два сечения суммы идентифицируемых зависимостей m_∑=m_z(α)+m_z(δ_вi) при i=1 (позиция 4) и i=2(позиция 5 как функций аргумента α. Номера точек на фиг. 2 те же, что и на фиг. 1.

Для первого сечения:	точка 1. m∑(α1,δ1)=mz(α1)+mz(δ1);
	точка 2. m∑(α2,δ1)=mz(α2)+mz(δ1).
Для второго сечения:	точка 3. m∑(α2,δ2)=mz(α2)+mz(δ2);
	точка 4. m∑(α3,δ2)=mz(α3)+mz(δ2).

- Из этих соотношений определяется искомое значение m_∑(α₃,δ₁):

m_∑(α₃,δ₁)=m_∑(α₃,δ₂)+m_∑(α₂,δ₁)-m_∑(α₂,δ₂).

- На этом итерационный шаг заканчивается. Результат шага: три точки m_z(α₁), m_z(α₂), m_z(α₃), принадлежащие одному сечению δ_в=δ₁, причем две точки: (α₁,δ₁), (α₃,δ₃), как и после проведения 1-го сечения, пригодны для продолжения итераций (проведения сечений по α).

- После к-й итерации алгоритма будет определена совокупность точек m_z(α_i)+m_z(δ_i), i=1, k+1, т.е. составляющая m_z(α) исходной суммы, восстановленная с точностью до константы. Итерации прекращают, если достигнута необходимая полнота восстановления составляющей (т.е. в каждом достаточно малом под интервале изменения аргумента восстановлено, хотя бы одно значение функции).

Составляющая m_z(δ_в) восстанавливается аналогичным образом: строятся сечения по α и точки всех сечений приводятся к одному сечению.

2. Для идентификации зависимости коэффициента подъемной силы от угла отклонения руля высоты с_у(δ_в) и зависимости коэффициента подъемной силы от угла атаки с_у(α) способ реализуется следующим образом.

Коэффициент подъемной силы ЛА определяется по измеренным на режиме исследования в связанной системе координат перегрузкам n_x1 и n_y1 и углу атаки:

c_y(α,δ_в)=G(n_x1sin(α)+n_y1cos(α))/Sq,

где

q - скоростной напор;

S - характерная площадь ЛА;

G - вес ЛА.

Далее составляющие коэффициента подъемной силы с_у(α) и с_у(δ_в) восстанавливаются по той же схеме, что и составляющие момента тангажа.

3. Для идентификации зависимости коэффициента момента тангажа ЛА от угловой скорости тангажа m_z(ω_z) и зависимости коэффициента момента тангажа ЛА от угла атаки m_z(α) способ реализуется следующим образом.

На привод руля высоты подается импульсный сигнал, удовлетворяющий двум требованиям на участке постоянного значения руля высоты (после выполнения импульса): 1) диапазоны изменения параметров ω_z, α не меньше диапазонов, в которых требуется восстановить зависимости m_z(α) и m_z(ω_z); 2) каждое сечение зависимости α(ω_z) прямой ω z = ω z 0 = c o n s t (прямой α=α⁰=const), где значение ω z 0 (значение α⁰), принадлежит требуемому диапазону определения зависимости m_z(ω_z), (m_z(α), содержит не менее двух точек. Импульсное отклонение рулевых поверхностей ЛА широко используется в практике летных испытаний.

Дальнейшая схема определения зависимостей m_z(ω_z), m_z(α) на участке постоянного значения руля высоты не отличается от ранее приведенной схемы определения m_z(α) и m_z(δ_в) при формальной замене параметра δ_в на параметр ω_z.

Таким образом, предложенный способ обеспечивает идентификацию двух составляющих коэффициента подъемной силы или аэродинамического момента тангажа по известной сумме составляющих и известным аргументам составляющих без каких-либо предположений о нелинейности составляющих, за исключением их однозначной зависимости от своих аргументов.

Для уменьшения накапливающихся при итерациях погрешностей следует минимизировать необходимое количество итераций за счет: выбора начального сечения; использования для последующей итерации не одной, а всех точек, пригодных для продолжения на текущей итерации; отбора - после окончания итераций - точек, полученных после наименьшего числа итераций среди точек, равномерно покрывающих диапазон изменения аргумента.

Пример

Для идентификации зависимости коэффициента продольного момента ЛА от угла отклонения руля высоты m_z(δ_в) и зависимости коэффициента продольного момента ЛА от угла атаки m_z(α) способ реализуется следующим образом.

Для обеспечения колебательного характера изменения параметров α и δ_в в короткопериодическом продольном движении ЛА выбирают тест-сигнал, равным:

δ_тест(t)=8°, при t∈[0,0.5] с;

δ_тест(t)=20°sin(2*(t-0.5))+8°, при t∈[0.5,4] c.

Продольное короткопериодическое движение ЛА в окрестности балансировочных значений α=24°, δ_в=8° с учетом работы автопилота описывается следующими уравнениями:

;

;

ω_z(0)=0°^/ _c; α(0)=24°; δ_в(0)=8°; t∈[0,4] c,

где

ω_z - угловая скорость тангажа;

- производная (по времени t) угловой скорости тангажа;

L - характерная длина ЛА;

q - скоростной напор;

m_z(ω_z), m_z(α), m_z(δ_в) - составляющие продольного аэродинамического момента от угловой скорости тангажа, угла атаки, угла отклонения руля высоты соответственно

J_z- момент инерции ЛА относительно оси ОZ связанной системы координат;

- производная (по времени t) угла атаки ЛА;

Y - подъемная сила ЛА;

υ - угол тангажа ЛА;

m - масса ЛА;

V - скорость полета ЛА;

- производная (по времени t) угла отклонения руля высоты

k, i_ω, i_α - коэффициенты контура автопилота.

Проводят измерения параметров полета ЛА (угла атаки, угловой скорости, угла отклонения руля высоты, скоростного напора) на интервале времени t∈[0,4] с под воздействием данного тест-сигнала. Фазовая траектория - зависимость α(δ_в) (позиция 15) представлена на фиг. 5.

Определяют по этим измерениям сумму (t) идентифицируемых зависимостей m_z(α), m_z(δ_в) с привлечением априорных данных о зависимости m_z(ω_z) и использовании операции цифрового дифференцирования зависимости ω_z(t) для получения ω ′ z ( t ) следующим образом:

Строят последовательность сечений фазовой траектории поочередно по каждому из аргументов α и δ_в таким образом, чтобы в двух последовательных сечениях содержалась как минимум одна и та же точка фазовой траектории.

На фиг. 3 и фиг. 4 показаны результаты нескольких итераций восстановления зависимостей m_z(α), m_z(δ_в).

Каждая i-я итерация восстановления зависимости m_z(α) состоит из проведения очередного сечения δ_в=δ_i фазовой траектории по δ_в (после проведения вспомогательного сечения по α, удовлетворяющего изложенному выше условию наличия общей точки) и объединения точек зависимости m_z(α,δ_i)=m_∑(α,δ_i), содержащихся в сечении, с совокупностью точек зависимости m_z(α)+const=m_z(α,δ₁), полученных на предыдущих итерациях.

Каждая i-я итерация восстановления зависимости m_z(δ_в) состоит из проведения очередного сечения α=α_i фазовой траектории по α (после проведения вспомогательного сечения по δ_в, удовлетворяющего изложенному выше условию наличия общей точки) и объединения точек зависимости mz(α_i,δ_в)=m_∑(α_i,δ_в), содержащихся в сечении, с совокупностью точек зависимости m_z(δ_в)+const=m_z(α_i,δ_в), полученных на предыдущих итерациях.

Цифры на графиках соответствуют номеру итерации, каждой итерации соответствует своя шкала слева от графика: позиция 7 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(α) на итерации №0 (метод сечений), позиция 8 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(α) на итерации №2, позиция 9 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(α) на итерации №4, позиция 10 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(α) на итерации №5, позиция 11 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(δ_в) на итерации №0 (метод сечений), позиция 12 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(δ_в) на итерации №2, позиция 13 - экспериментальные точки восстановленной - с точностью до константы - зависимости m_z(δ_в) на итерации №4. Для сравнения на этих же фигурах сплошными линиями приведены истинные зависимости m_z(α) (позиция 6) и m_z(δ_в) (позиция 14).

Таким образом, предложенный способ позволил идентифицировать с точностью до констант нелинейные зависимости m_z(α), m_z(δ_в) при плохой обусловленности задачи идентификации (зависимость α(δ_в) близка к линейной), обусловленной обратной связью по α в контуре автопилота.

Способ непараметрической идентификации по результатам летных исследований двух нелинейных аэродинамических характеристик летательного аппарата: зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угла отклонения руля высоты, или зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угловой скорости тангажа, или зависимости коэффициента подъемной силы от угла атаки и зависимости коэффициента подъемной силы от угла отклонения руля высоты, включающий подачу на привод руля высоты летательного аппарата тестового сигнала, возмущение движения летательного аппарата, измерение параметров движения летательного аппарата, обработку измерений для получения аргументов идентифицируемых зависимостей: угла атаки и угла отклонения руля высоты, или угла атаки и угловой скорости тангажа, а также зависимости коэффициента аэродинамического момента тангажа, или зависимости коэффициента подъемной силы, от указанных аргументов, отличающийся тем, что при условии, что идентифицируемые зависимости в области определения являются однозначными функциями своих аргументов и аддитивными составляющими зависимости коэффициента аэродинамического момента тангажа, либо коэффициента подъемной силы, от указанных аргументов, идентифицируемые зависимости определяются следующим образом: на привод руля высоты летательного аппарата осуществляют подачу тестового сигнала, обеспечивающего колебательный характер изменения по времени аргументов идентифицируемых зависимостей на исследовательском режиме полета летательного аппарата таким образом, чтобы диапазоны изменений аргументов идентифицируемых зависимостей были не менее диапазонов, для которых требуется идентифицировать зависимости, а фазовая траектория (то есть зависимость одного аргумента от другого аргумента) была бы замкнутой; затем после получения из обработки измерений параметров полета трех функций времени: двух аргументов идентифицируемых зависимостей и суммы идентифицируемых зависимостей, строят последовательность сечений фазовой траектории поочередно по каждому из аргументов таким образом, чтобы в двух последовательных сечениях содержалась как минимум одна и та же точка фазовой траектории, что позволяет объединить все точки всех построенных сечений в две совокупности, каждая из которых представляет собой - с точностью до константы - поточечное отображение идентифицируемых зависимостей: зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угла отклонения руля высоты, или зависимости коэффициента аэродинамического момента тангажа от угла атаки и зависимости коэффициента аэродинамического момента тангажа от угловой скорости тангажа, или зависимости коэффициента подъемной силы от угла атаки и зависимости коэффициента подъемной силы от угла отклонения руля высоты.