Троичный т-триггер и троичный реверсивный счетчик на его основе

Троичный т-триггер и троичный реверсивный счетчик на его основе

Иллюстрации

Показать все

Реферат

Группа изобретений относится к устройствам цифровой вычислительной техники, в частности к недвоичной технике, и предназначена для создания реализуемых в среде полупроводниковой интегральной электроники троичных Т-триггеров и счетчиков.

Известной успешной реализацией недвоичных цифровых устройств являются троичные ЦВМ "Сетунь" и "Сетунь 70" [1, 2]. Логические элементы этих ЦВМ выполнены на основе электромагнитной техники [8, 9], имеют малое быстродействие, большие потребляемую мощность и размеры. Реализация устройств на таких элементах, не может быть осуществлена в среде современной полупроводниковой интегральной электроники.

Известен функциональный аналог элементов ЦВМ "Сетунь" - "Пороговый Элемент Троичной Логики" (ПЭТЛ), реализуемый в среде современной полупроводниковой интегральной электроники [3]. На ПЭТЛ, используя специальную ПЭТЛ-схемотехнику [7], можно создавать троичные цифровые устройства. Ассортимент средств, которыми в настоящее время располагает ПЭТЛ-схемотехника, недостаточен для создания всего спектра троичных устройств. В частности, в нем отсутствуют троичные Т-триггер и счетчик.

Задача, решаемая заявляемой группой изобретений, направлена на пополнение ассортимента средств ПЭТЛ-схемотехники троичным Т-триггером и Троичным реверсивным счетчиком, благодаря чему поддерживается реализация в среде интегральной полупроводниковой электроники более широкого набора логических и операционных устройств, использующей симметричную троичную систему с цифрами -1, 0, +1.

Наиболее близким техническими решениями к заявляемой группе изобретений являются группы изобретений: "Пороговый Элемент Троичной Логики и устройства на его основе" [3], "Узел Троичной схемотехники и дешифраторы-переключатели на его основе" [4] и Троичный D-триггер (варианты) [5].

Известная группа изобретений имеет ограниченные возможности, так как поддерживает реализацию комбинационных схем: троичной схемы "И", троичного полусумматора, троичных дешифраторов, переключателей на разное число направлений и схем с памятью: четырех вариантов троичных D-триггеров с управлением по уровню сигнала и по его фронту. Реализацию троичного триггера со счетным входом (Т-триггера) и Троичного реверсивного счетчика известная группа изобретений не раскрывает.

Раскрытие изобретения

Первым аспектом изобретения является Троичный Т-триггер (ТТТ), содержащий узел троичной схемотехники (УТС), троичный полусумматор (ТПС), троичный D-триггер (ТDТ) пороговые элементы троичной логики (ПЭТЛ).

Вход первого ПЭТЛ соединен с входом Dвx ТТТ, вход В ТПС соединен с входом Т ТТТ, вход С УТС соединен с входом С2 ТТТ, вход С TDT соединен с входом С1 ТТТ, +R и -R выходы соответственно второй и третьей секций ТПС соединены с выходом ПЕРЕНОС ТТТ, +R выход первого ПЭТЛ и третий выход УТС соединены с входом второго ПЭТЛ, -R выход первого ПЭТЛ и шестой выход УТС соединены с входом третьего ПЭТЛ, +L выход первой секции ТПС, +L выход второй секции ТПС, -L выход третьей секции ТПС и седьмой выход УТС соединены с входом четвертого ПЭТЛ, -L выход первой секции ТПС, +L выход второй секции ТПС, -L выход третьей секции ТПС и второй выход УТС соединены с входом пятого ПЭТЛ, +R выходы второго и четвертого ПЭТЛ и -R выходы третьего и пятого ПЭТЛ соединены с D входом TDT, +R и -R выходы TDT соединены с входом А ТПС, +R и -R выходы TDT соединены с выходом Q ТТТ, +L и -L выходы TDT соединены с выходом НЕ Q ТТТ.

Вторым аспектом изобретения является Троичный k-разрядный Реверсивный Счетчик (ТРС), содержащий k Троичных Т-триггеров (ТТТ) из п. 1 и два пороговых элемента троичной логики (ПЭТЛ).

Вход Т первого ТТТ соединен с входом PC (Режимы Счета) ТРС, вход X первого ПЭТЛ соединен с входом РР (Режимы Работы) ТРС, вход X второго ПЭТЛ соединен с входом Сч ТРС, выход П j-го ТТТ соединен с входом Т (j+1)-го ТТТ, (j=1, 2…(k-1)), выход П k-го ТТТ соединен с земляной шиной, вход Dвx j-го ТТТ соединен с входом Dj ТРС, выход Q j-го ТТТ соединен с выходом Qj ТРС, Вход НЕ Q j-го ТТТ соединен c выходом НЕ Qj ТРС, +R и -R выходы j-ой группы первого ПЭТЛ соединены с входом C2 j-го ТТТ, +R и -R выходы j-ой группы второго ПЭТЛ соединены с входом C1 j-го ТТТ (j=1, 2… k).

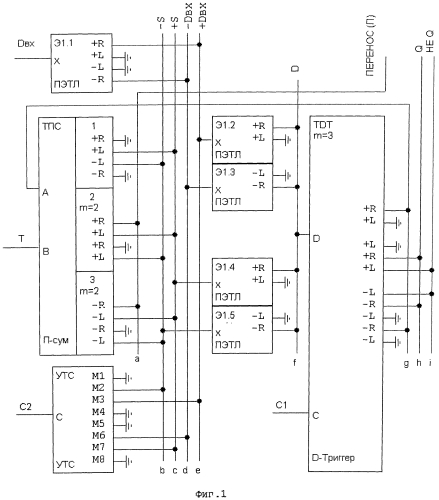
На Фиг.1 изображен Троичный Т-триггер. На Фиг.2а и 2б даны полное и условное изображения Троичного Полусумматора. Фиг.3 содержит условное изображение Троичного D-триггера. На Фиг.4 дано условное изображение Троичного Т-триггера. На Фиг.5 изображен Троичный Реверсивный Счетчик.

Троичный Т-триггер (ТТТ) и Троичный реверсивный счетчик (ТРС) выполнены на основе ПЭТЛ-схемотехники, под которой подразумевается совокупность элементов, узлов, правил их соединения, приемов, типовых схемных решений и изобразительных средств, поддерживающих реализацию цифровых устройств в троичной системе с цифрами +1, 0, -1.

ПЭТЛ-схемотехника появилась недавно (первый патент был получен в 2009 году) и отличается от других интегральных схемотехник (ТТЛ, К-МОП, ЭСЛ). Она описана в [3, 4, 5, 6, 7]. Краткие сведения о ПЭТЛ-схемотехнике приведены ниже:

1. Троичным значениям +1, 0, -1 на физическом уровне соответствуют дискретные токи +I_Ф, 0, -I_Ф. Эти же токи протекают в цепях межэлементных связей.

2. Базовый элемент ПЭТЛ-схемотехники - Пороговый Элемент Троичной Логики (ПЭТЛ) - имеет 1 вход и группу из 4-х выходов: +R, +L, -L, -R.

3. Узел Троичной Схемотехники (УТС), состоит из 3-х ПЭТЛ, имеет 1 вход и группу из 8 выходов: М1, М2, М3, М4, М5, М6, М7, М8.

4. ПЭТЛ и УТС могут иметь более одной группы выходов. Значения на одноименных выходах тождественны.

5. На входах ПЭТЛ и УТС происходит алгебраическое сложение разнонаправленных дискретных токов +I_Ф, и -I_Ф и формируется троичное значение X. Если число +I_Ф больше числа -I_Ф-Х=+1, если число +I_Ф меньше числа -I_Ф-Х=-1, если число +I_Ф равно числу -I_Ф-Х=0.

Значения X представлены на выходах ПЭТЛ и УТС парами их двузначных компонент. Соответствие значений компонент значениям X приведено в Таблице 1. Варианты пар пронумерованы арабскими цифрами, компоненты в паре - римскими.

Таблица 1
	Варианты пар двузначных компонент X
1		2		3		4
	X	+1	0	-1	X	+1	0	-1	X	+1	0	-1	X	+1	0	-1
I	+R,M1	+1	0	0	+L,M2	0	+1	+1	М5	0	0	+1	М6	+1	+1	0
II	-R,M4	0	0	-1	-L,M3	-1	-1	0	М8	-1	0	0	М7	0	-1	-1

В Таблице 1 фигурируют троичные значения, однако сами компоненты двоичны: компоненты в строке I имеют значения+1 или 0; компоненты в строке II - -1 или 0.

Терминология ПЭТЛ-схемотехники не устоялась. Далее будут использоваться сопоставимые термины из двоичной схемотехники и из лексикона "Сетуней". Во избежание недоразумений следует руководствоваться таблицами истинности.

Алгебраическое сложение разнонаправленных дискретных токов на входах элементов и объединение (сборка) их выходов являются приемами ПЭТЛ-схемотехники. Так, объединяя +R и -R, получим повторение входного троичного значения X, объединяя +L и -L - его нециклическую инверсию, объединяя +R и +L или -R и -L - постоянные значения +1 или -1 для любого значения X на входе. Практикуется объединение выходов разных ПЭТЛ и УТС.

Сборки изображаются вертикальными линиями, нижние концы которых помечены буквами, а верхние - либо наименованием элемента, ко входу которого сборка подключена, либо названием сигнала. Слева от сборки располагаются элементы, выходы которых к ней подключены, справа - элементы, на входах которых формируются значения X.

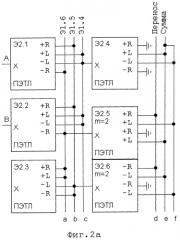
Помимо ПЭТЛ с полным набором выходов можно применять элементы с половинным числом выходов: либо только +R, +L, либо только -L, -R. Если у ПЭТЛ или УТС несколько групп тождественных выходов, их число m указывается под номером элемента: (на Фиг.2а у ПЭТЛ Э2.5 только положительные выходы, у ПЭТЛ Э2.6 - только отрицательные; оба ПЭТЛ имеют по 2 группы выходов - m=2). Если выход ПЭТЛ не используют, его соединяют с земляной шиной.

Проиллюстрируем возможности ПЭТЛ-схемотехники на примере Троичного полусумматора [3] (Фиг.2а). Полусумматор реализован на 6 ПЭТЛ Э2.1-Э2.6. Он выполняет поразрядное сложение двух троичных значений А и В на входах, формируя на выходах Сумма и Перенос троичные значения в соответствии с Таблицей 2.

Таблица 2
Троичный полусумматор
А	+1	0	-1	+1	0	-1	+1	0	-1
В	+1	+1	+1	0	0	0	-1	-1	-1
а	+1	0	0	0	-1	-1	0	-1	-1
b	+1	+1	0	+1	+1	0	0	0	-1
с	-1	-1	0	-1	0	+1	0	+1	+1
е	0	+1	+1	+1	+1	0	+1	0	+1
f	-1	0	-1	0	-1	-1	-1	-1	0
Сумма (e+f)	-1	+1	0	+1	0	-1	0	-1	+1
Перенос (d)	+1	0	0	0	0	0	0	0	-1

Помимо значений на входах и выходах Троичного полусумматора (ТПС) в Таблице приводятся промежуточные значения на сборках a, b, d, e, f. Алгоритм заполнения ячеек таблицы следующий:

1. Берут значения А и В из столбца, в котором стоит ячейка;

2. Определяют значения на выходах ПЭТЛ, подключенных к сборке ячейки, соответствующие выбранным А и В;

3. Определяют значение X на сборке (на входе подключенного к сборке ПЭТЛ) и заносят его в ячейку;

4. Переходят к другой ячейке таблицы (одной сборке соответствуют 9 ячеек) и берут другие значения А и В.

5. По завершению переходят к ячейкам других сборок.

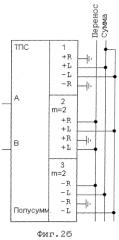
Если отдельные узлы используются часто, их (подобно УТС) изображают условно (без подробностей) - в виде прямоугольников. В ПЭТЛ-схемотехнике все узлы состоят из ПЭТЛ, поэтому к их входам и выходам применяемо все относящееся к ПЭТЛ: На входах узла суммируются разнонаправленные дискретные токи и узел может иметь более одной группы выходов. Если выходы (группы выходов) имеют разное назначение, их делят на секции.

Условное изображение ТПС дано на Фиг.2б. В нем три секции: 1, 2 и 3; в секциях 2 и 3 по 2 группы выходов. В таком виде ТПС фигурирует далее в схеме троичного Т-триггера (ТТТ) на Фиг.1.

Другой составной частью ТТТ является Троичный D-триггер (TDT). Его устройство описано в патенте [5]. На Фиг.3 дано условное изображение TDT с тремя группами выходов. TDT запоминает троичное значение на входе данных D, когда значение на управляющем входе C изменяется (т.е по фронту сигнала на C).

Схема троичного Т-триггера (ТТТ) представлена на Фиг.1.

Изменение состояний Т-триггера происходят по фронту (переходу от -1 к +1 или от +1 к -1) на C1. Режимы работы определяется входом C2. Если C2=+1 (режим счета) - идет счет по модулю 3 числа фронтов, поступивших на C1, и результат помещается в TDT. Если C2=-1, (прием данных) по фронту на C1 происходит прием в TDT данных с входа Dвх. Если C2=0 (обнуление) - по фронту на C1 происходит сброс TDT в состояние 0. Режимы счета определяются входом Т. Если Т=+1 - идет счет на возрастание, если Т=-1 - идет счет на убывание, если Т=0 - счет останавливается. Содержимое TDT доступно в прямом и инверсном виде на выходах Q и НЕ Q.

Опишем функционирование Т-триггера в режиме счета (C2=+1). В Таблице 3 показаны значения: на входе Т, на выходе Q, на выходах Перенос(П) ТТТ и Сумма (S), на входе D TDT.

Таблица 3
№	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Т	+1	0	-1
Q	0	+1	-1	0	+1	-1	0	+1	-1	-1	-1	-1	-1	+1	0	-1	+1	0
S	+1	-1	0	+1	-1	0	+1	-1	-1	-1	-1	-1	+1	0	-1	+1	0	-1
П	0	+1	0	+1	0	+1	0	-1	0	-1	0

Прослежены изменения значений для 18-и последовательных этапов (с 0 по 17). Началом каждого этапа является фронт на C1. Предполагается что на начальном этапе Q=0. На этапах 0-7 Т=+1 (счет на увеличение); на этапах 8-11 Т=0 (счет остановлен); на этапах 12-17 Т=-1 (счет на уменьшение).

На вход А ТПС в начале каждого этапа с выхода TDT поступает предыдущее значение Суммы, записанное в TDT на предыдущем этапе. В ТПС оно суммируется по модулю 3 с текущим значением режима счета Т. На выходах ТПС формируются новые значения Суммы и Переноса. В строке П+1 и -1 выделены жирным. Таким образом частота поступления фронтов на С1 делится на 3.

Функционирование Т-триггера реализуется следующим образом:

1. ПЭТЛ Э1.1 формирует на сборках d и е двузначные компоненты +D_вх и -D_вх троичного значения D_вх (Таблица 1, 1-й вариант); компоненты поступают на входы ПЭТЛ Э1.2 и Э1.3.

2. ТПС формирует на сборках b и c двузначные компоненты +S и -S троичного значения Сумма (S) (Таблица 1, 2-й вариант); компоненты поступают на входы ПЭТЛ Э1.4 и Э1.5.

3. УТС формирует на сборках b, c, d, e сигналы, разрешающие или блокирующие (в зависимости от значения C2) прохождение компонент +D_вх, -D_вх (С2=-1) или +S1, -S1 (C2=+1) на сборку f, подключенную к входу D TDT. Компоненты объединяются на f и формируются троичные значения Сумма(S) или D_вх. Если С2=0, прохождение компонент блокируется и f=0. Значение (D_вх, S или 0) записываются в TDT.

П.п 1-3 отражены в Таблице 4. Символ X означает, что значение в ячейке может быть любым, поскольку выходы, фигурирующие в этой части таблицы, подключены не ко всем сборкам.

Таблица 4

Dвх=(+Dвх)+(-Dвх)

Сумма (S)=(+S)+(-S)

C2

+1

0

-1

+1

0

-1

+1

0

-1

b

X

X

X

b

-S

0

+1

+1

b

0

+1

+1

с

X

X

X

с

+S

-1

-1

0

с

0

-1

-1

d

-Dвх

0

0

-1

в

X

X

X

d

-1

-1

0

е

+Dвх

+1

0

0

e

X

X

X

e

+1

+1

0

f

Dвх

0

S

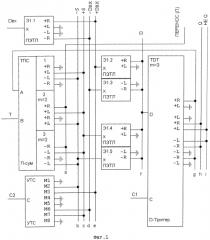
Условное изображение ТТТ приведено на Фиг.4. ТТТ входит в состав Троичного Реверсивного k-разрядного Счетчика (ТРС), изображенного на Фиг.5.

ТРС состоит из последовательно включенных Т-триггеров (ТТТ.1 -ТТТ.k) и двух ПЭТЛ (Э5.1 и Э5.2). Т-вход первого ТТТ является входом PC (Режим Счета) ТРС. Входы Т последующих ТТТ подключены к выходам П предыдущих. ПЭТЛ Э5.1 и Э5.2 разветвляют сигналы PC и Сч и подают их в параллель, на входы C2 и C1 ТТТ.

Изменения состояний счетчика происходят по фронтам сигнала на входе Сч. Текущие значения разрядов доступны в прямом и инверсном виде на выходах Qj и НЕ Qj. Содержимое счетчика может быть обнулено либо изменено приемом новых значений с входов Dj (j=1, 2… k).

ТРС функционирует в различных режимах, определяемых значениями на входах: РР (Режимы Работы) и РС (Режимы Счета) в соответствии с Таблицей 5.

Таблица 5
РР	+1	0	-1
Режимы работы	Счет разрешен	Обнуление	Прием с D
PC	+1	0	-1
Режимы счета	Прямой счет	Счет остановлен	Обратный счет

В режиме счета (РР=+1; РС=+1, 0, -1) текущие значения Сумм S=(+S)+(-S) на выходах ТПС в составе ТТТ в начале каждого этапа записываются в TDT, с выходов которых поступают на входы А ТПС. Там они суммируются по модулю 3 с текущими значениями на входах Т. Таким образом формируются новые значения S.

В режиме приема с D (РР=-1) записываемые значения подаются в параллель на входы D1-Dk, откуда по фронту на Сч помещаются в ТТТ.

В режиме обнуления (РР=0) по фронту на Сч в ТТТ записываются нули.

Работа ТРС в режиме счета (РС=+1, 0, -1) иллюстрируется Таблицей 6, в которой отображены изменения состояний разрядов ТРС Q1 и Q2, а также Сумм S1 и S2 на 36 этапах с 0 по 35.

Таблица 6
№	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
PC	+1	0
Q1	0	+1	-1	0	+1	-1	0	+1	-1	0	+1	-1	0	+1	-1	0	+1	+1
S1	+1	-1	0	+1	-1	0	+1	-1.	0	+1	-1	0	+1	-1	0	+1	+1	+1
П1	0	+1	0	+1	0	+1	0	+1	0	+1	0
Q2	0	0	+1	+1	+1	-1	-1	-1	0	0	0	+1	+1	+1	-1	-1	-1	-1
S2	0	+1	+1	+1	-1	-1	-1	0	0	0	+1	+1	+1	-1	-1	-1	-1	-1
П2	0	+1	0	+1	0
№	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
PC	0	-1	+1
Q1	+1	+1	+1	0	-1	+1	0	-1	+1	0	-1	+1	0	-1	+1	-1	0	+1
SI	+1	+1	0	-1	+1	0	-1	+1	0	-1	+1	0	-1	+1	-1	0	+1	-1
П1	0	-1	0	-1	0	-1	0	-1	+1	0	+1
Q2	-1	-1	-1	-1	-1	+1	+1	+1	0	0	0	-1	-1	-1	+1	-1	-1	-1
S2	-1	-1	-1	-1	+1	+1	+1	0	0	0	-1	-1	-1	+1	-1	-1	-1	0
П2	0	-1	0	-1	+1	0

Этап начинается Фронтом на входе Сч ТРС. Начальные значения Q1=Q2=0. На этапах с 0 по 15 и с 32 по 35 счет прямой; на этапах с 16 по 19 счет остановлен; на этапах с 20 по 31 - счет обратный. Из 36 фронтов, поступивших на Сч, 19 прибавлены к первоначальному содержимому счетчика, 12 отняты и 4 не посчитаны. На 35 этапе формируется значение 7=19-12 (в троичной форме +1 -1 +1). Младшие разрядов Q2 и Q1 в столбце №35 выделены жирным шрифтом. Также выделены +1 и -1 на выходах П1 и П2.

Описание работы первого разряда содержится в Таблице 3. Во втором и последующих разрядах счет происходит, если П≠О. Таким образом, частота поступления фронтов на Сч делится на 3, 9, 27… 3k.

Литература

1. Брусенцов Н.П., Маслов С.П., Розин В.П., Тишулина A.M.

Малая цифровая вычислительная машина "Сетунь". - М.: Изд-во Московского университета, 1965, 145 с.

2. Брусенцов Н.П., Жоголев Е.А., Маслов С.П., Рамиль Альварес X. Опыт создания троичных цифровых машин. // Компьютеры в Европе. Прошлое, настоящее и будущее. - Киев: Феникс, 1998. С.67-71.

3. Маслов С.П. Пороговый элемент троичной логики и устройства на его основе. Патент РФ на изобретение RU №2394366 C1. Зарегистрирован: 10.07.2010.

4. Маслов С.П. Узел троичной схемотехники и дешифраторы - переключатели на его основе. Патент РФ на изобретение RU №2461122 C1. Зарегистрирован: 10.09.2012.

5. Маслов С.П. Троичный D-триггер (варианты). Патент РФ на изобретение. RU №2510129 C1. Зарегистрирован: 20.03.2014.

6. Маслов С.П. Об одной возможности реализации троичных цифровых устройств. Тематический сборник №12 "Программные системы и инструменты", М.: Изд-во факультета ВМиК МГУ, 2011. С.222-227.

7. Маслов С.П. Троичная схемотехника. Тематический сборник №13 "Программные системы и инструменты", М.: Изд-во факультета ВМиК МГУ, 2012. С.152-158.

8. Брусенцов Н.П. Пороговая реализация трехзначной логики электромагнитными средствами. // Вычислительная техника и вопросы кибернетики. Вып.9. - М.: Изд-во Моск. ун-та, 1972. С.3-35.

9. Брусенцов Н.П. Электромагнитные цифровые устройства с однопроводной передачей трехзначных сигналов. - В кн.: Магнитные элементы автоматики и вычислительной техники. XIV Всесоюзное совещание (Москва, сентябрь 1972 г.). М.: Наука, 1972, с.242-244.

1. Троичный Т-триггер (ТТТ) содержит узел троичной схемотехники (УТС), троичный полусумматор (ТПС), D-триггер (TDT) и пять пороговых элементов троичной логики (ПЭТЛ), причем TDT имеет 3 группы выходов, причем второй и четвертый ПЭТЛ имеют только положительные выходы, третий и пятый ПЭТЛ имеют только отрицательные выходы, причем вход первого ПЭТЛ соединен с входом Dвx ТТТ, вход В ТПС соединен с входом Т ТТТ, вход С УТС соединен с входом С2 ТТТ, вход С ТDТ соединен с входом С1 ТТТ, причем второй положительный R выход второй секции ТПС и второй отрицательный R выход третьей секции ТПС через первую сборку соединены с выходом ПЕРЕНОС ТТТ, причем положительный R выход первого ПЭТЛ и третий выход УТС через пятую сборку соединены с входом второго ПЭТЛ, причем отрицательный R выход первого ПЭТЛ и шестой выход УТС через четвертую сборку соединены с входом третьего ПЭТЛ, причем положительный L выход первой секции ТПС, второй положительный L выход второй секции ТПС, второй отрицательный L выход третьей секции ТПС и седьмой выход УТС через третью сборку соединены с входом четвертого ПЭТЛ, причем отрицательный L выход первой секции ТПС, первый положительный L выход второй секции ТПС, первый отрицательный L выход третьей секции ТПС и второй выход УТС через вторую сборку соединены с входом пятого ПЭТЛ, причем положительные R выходы второго и четвертого ПЭТЛ и отрицательные R выходы третьего и пятого ПЭТЛ через шестую сборку соединены с D входом TDT, причем третий положительный и первый отрицательный R выходы TDT через седьмую сборку соединены с входом А ТПС, причем первый положительный и второй отрицательный R выходы TDT через восьмую сборку соединены с выходом Q ТТТ, причем первый положительный и третий отрицательный L выходы TDT через девятую сборку соединены с выходом НЕ Q ТТТ, причем положительный L и отрицательный L выходы первого ПЭТЛ, положительный и отрицательный R выходы первой секции ТПС, первый положительный R выход второй секции ТПС, первый отрицательный R выход третьей секции ТПС, первый, четвертый, пятый и восьмой выходы УТС, положительные L выходы второго и четвертого ПЭТЛ, отрицательные L выходы третьего и пятого ПЭТЛ, третий и второй положительные L выходы TDT, второй и первый отрицательные L выходы TDT соединены с земляной шиной.

2. Троичный Реверсивный Счетчик (ТРС) содержит k Троичных Т-триггеров (ТТТ) из п. 1 и два пороговых элементов троичной логики (ПЭТЛ), причем ПЭТЛ имеют k групп выходов, причем k - число разрядов ТРС, причем вход Т первого ТТТ соединен с входом PC (Режим Счета) ТРС, причем вход X первого ПЭТЛ соединен с входом РР (Режим Работы) ТРС, причем вход X второго ПЭТЛ соединен с входом Сч ТРС, причем выход П j-го ТТТ соединен с входом Т (j+1)-го ТТТ, причем j=1, 2…(k-1), причем выход П k-го ТТТ соединен с земляной шиной, причем вход Dвx j-го ТТТ соединен с входом Dj ТРС, причем выход Q j-го ТТТ соединен с выходом Qj ТРС, причем выход НЕ Q j-го ТТТ соединен с выходом НЕ Qj ТРС, причем положительный и отрицательный R выходы j-ой группы первого ПЭТЛ через сборку bj соединены с входом С2 j-ro ТТТ, причем положительный и отрицательный R выходы j-ой группы второго ПЭТЛ через сборку aj соединены с входом C1 j-го ТТТ, причем положительный и отрицательный L выходы j-ых групп первого и второго ПЭТЛ соединены с земляной шиной, причем j=1, 2…k.