Генератор псевдослучайной функции

Генератор псевдослучайной функции

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике, в частности к генераторам псевдослучайных функций (ПСФ), и может быть использовано в цифровых вычислительных устройствах, а также в системах защиты информации. В работе [1] (Naor M., Reingold О. Constructing Pseudo-Random Permutations with a Prescribed Structure // Journal of Cryptology. 2002. №15. P. 97-102) представлен алгоритм вычисления псевдослучайной функции Naor-Reingold, которая в качестве аргументов использует ключ (h, х₁…x_m) и входные данные в двоичном коде b=b₁, b₂…b_mX{0,l}^m

F N R ( ( h , x 1 , x 2 , … , x m ) ( b 1 , … , b m ) ) = h П i m = 1 x i b i mod p       ( 1 )

где h - первообразной элемент мультипликативной группы, порожденный простым числом р: m - разность двоичный кода.

С целью сокращения времени вычисления значений псевдослучайной функции в работе [2] (Калмыков И.А. Разработка псевдослучайных функций повышенной эффективности [Текст] / И.Л. Калмыков, О.И. Дагаева // Известия ЮФУ Технические науки. Тематический выпуск «Информационная безопасность». 2011. Вып. 12. С. 160-169) был предложен алгоритм получения ПСФ

F П С Ф ( ( h , x 1 , x 2 , … , x m ) ( u 1 , … , u n ) ) = h П i = 2 m 1 ( X i + U i ) mod p       ( 2 )

где U=U₁,U₂… - входной код; X=X₁,X₂… - ключ; log₂X=log₂U=m - разрядность двоичного кода; n = m e   - количество блоков; l=log₂U_i=log₂X_i - разрядность блока. Применение алгоритма (2) позволяет сократить время вычисления ПСФ в l раз, по сравнению с классической реализацией (1).

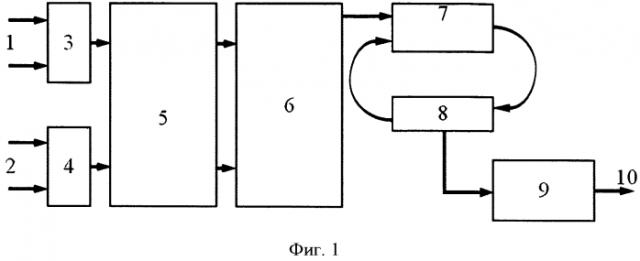
На фиг. 1 представлена схема генератора псевдослучайной функции. Он содержит первый вход 1, второй вход 2, регистр 3, регистр 4, сумматор 5 по модулю р, блок 6 вычисления обратного элемента по модулю р, умножитель 7 по модулю р, третий регистр 8, блок 9 возведения в степень по модулю р, выход устройства 10.

Входы первого и второго регистров 3 и 4 подключены к первому входу 1 и второму входу 2 генератора соответственно. Выходы регистров 3 и 4 подсоединены ко входу сумматора 5 по модулю р, выход которого подсоединен ко входу блока 6 вычисления обратного элемента по модулю р. Выход блока 6 вычисления обратного элемента по модулю р подключен к первому входу умножителя 7 по модулю р, второй вход которого подсоединен к первому выходу третьего регистра 8. Вход третьего регистра 8 подсоединен к выходу умножителя 7 по модулю р, а второй выход регистра 8 подключен к блоку 9 возведения в степень по модулю р, выход которого является выходом 10 устройства.

Пример. Пусть р=11. В качестве первообразного элемента выбираем h=2. Пусть в качестве секретного ключа используется Х=8₁₀. В качестве входного значения, поступившего в генератор ПСФ, U=10₁₀. Представим эти значения в двоичном коде. Получаем U=10₁₀=1010₂; Х=8₁₀=1000₂.

Разобьем эти значения на 2 блока, по 2 бит каждый. Имеем

U₁=10₂=2₁₀; U₂=l0₂=2₁₀; Х₁=10₂=2₁₀; Х₂=00₂=0₁₀.

Воспользуемся выражением (2).

Получаем

F П С Ф = h П i = 1 2 1 ( X i + U i ) mod p = 2 1 ( 2 + 2 ) ∗ 1 ( 2 + 0 ) mod 11 = 2 1 4 ∗ 1 2 mod 11 = 2 1 8 mod 11 = 2 7 mod 11 = 7

Рассмотрим работу устройства. Перед началом работы генератора в третий регистр 8 записывается единица. На первый вход 1 подается в двоичном коде первый блок секретного ключа X₁=10₂, который записывается в первый регистр 3. На второй вход 2 поступает первый блок входного кода U₁=10₂, который записывается в о второй регистр 4. С выходов регистров 3 и 4 значение Х₁ и U₁ поступают на входы сумматора 5 по модулю р=11, на входе которого появляется результат (Х₁+U₁)mod р=(10₂+10₂) mod 11=4₁₀.

Данное значение подается на вход блока 6 вычисления обратного элемента по модулю р=11. Работа этого блока представлена в таблице 1.

Таблица 1
Элемент а	1	2	3	4	5	6	7	8	9	10
Обратный элемент по модулю p=11, a-1	1	6	4	3	9	2	8	7	5	10

С выхода блока 6 снимается значение 3, которое поступает на первый вход умножителя 7 по модулю р=11, на второй вход которого поступает 1 с первого выхода третьего регистра 8. Умножитель 7 выполняет вычисления

3∗1mod11=3

и полученный результат записывается в регистр 8.

Затем па первый и второй входы 1 и 2 соответственно подаются вторые блоки секретного ключа Х₂=00₂=0₁₀ и входных данных U₂=10₂=2₁₀. Данные значения записываются в регистр 3 и регистр 4 соответственно. С входа регистров данные блоки поступают на входы сумматора 5 по модулю 11, где реализуется процедура

(X₂+U₂)modp=(00₂+10₁)mod11=2

Вычисленное значение подается на вход блока 6 вычисления обратного элемента по модулю р=11. Согласно таблице 1 с выхода блока 6 будет снято число 6, которое поступит на первый вход умножителя 7 по модулю р=11. На второй вход подается число 3 с первого выхода третьего регистра 8, который используется в качестве хранилища промежуточных результатов. На выходе умножителя 7 по модулю р=11 появляется результат

(6∗3)mod 11=18mod11=7

Вычисленное значение поступает в третий регистр 8. Так как вычисления закончены, то что значение со второго выхода регистра 8 подается на вход блока 8 возведения в степень по модулю р=11, который реализует процедуру (2). В результате имеем

F(2,8,10)=2⁷mod11=7

Проведем сравнительную оценку времени вычисления ПСФ согласно алгоритму, задаваемому выражением (1), и алгоритму (2). Анализ этих выражений показывает, что основным фактором, от которого будет зависеть время характеристики генератора ПСФ, будут вычисления показателя степени. Из выражения (1) наглядно видно, чтобы реализовать эту процедуру необходимо выполнить (m-1) умножений данных размером ]log₂p[.

При использовании выражения (2) число таких умножений сокращается в L раз.

где - l=log₂U_i=log₂X_t - разность блоков.

Таким образом, очевидно, что применение выражения (2) позволяет повысить быстродействие генератора ПСФ в l раз по сравнению с вычислением ПСФ согласно (1).

Генератор псевдослучайной функции, отличающийся тем, что генератор содержит первый и второй входы, которые являются входами первого и второго регистров, выходы которых соответственно подключены к первому и второму входам сумматора по модулю р, выходы которого подсоединены ко входу блока вычисления обратного элемента по модулю р, выход блока вычисления обратного элемента по модулю р подсоединен к первому входу умножителя по модулю р, выход умножителя по модулю р соединен со входом третьего регистра, первый выход которого соединен со вторым входом умножителя по модулю р, второй выход третьего регистра соединен со входом блока возведения в степень по модулю р, выход которого является выходом генератора.