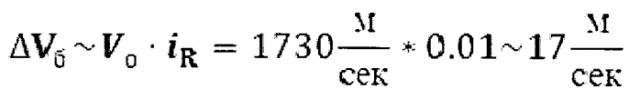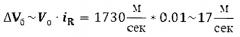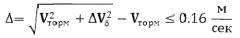Способ управления движением активного космического объекта, стыкуемого с пассивным космическим объектом

Способ управления движением активного космического объекта, стыкуемого с пассивным космическим объектом

Иллюстрации

Показать все

Реферат

Предлагаемый способ управления может быть использован в космической технике при сближении и последующей стыковке двух космических объектов, находящихся на орбитах различных небесных тел, например космического корабля (КК), находящегося на орбите вокруг Земли в качестве активного космического объекта (АКО) и орбитальной станции (ОС), находящейся на орбите вокруг любого небесного тела, например Луны (ЛОС) в качестве пассивного космического объекта (ПКО).

Известен способ управления, выбранный в качестве аналога, в котором для обеспечения сближения и последующей стыковки двух космических объектов, АКО выводится в плоскость орбиты ПКО. После выведения АКО переводится на так называемую орбиту фазирования, располагающуюся между начальной орбитой АКО и орбитой ПКО для ликвидации начального углового рассогласования между двумя объектами, т.к. находясь на разных орбитах, АКО и ПКО имеют разные угловые скорости вращения вокруг небесного тела. После нескольких витков (число определяется выбранной баллистической схемой сближения) АКО, с помощью двухимпульсного маневра, переводится в окрестность ПКО, где сближение завершается автоматической стыковкой. Такой способ управления активным кораблем применяется при сближении и стыковке КК с ОС [1. Р.Ф. Аппазов, О.Г. Сытин «Методы проектирования траекторий носителей и спутников Земли», Наука, Москва, 1987]. Основным недостатком такого способа управления является то, что для перехода АКО с орбиты выведения на орбиту ПКО и проведения сближения необходимо затратить дополнительное топливо на переход с орбиты фазирования на орбиту ПКО и время на проведение фазирования.

Известен способ управления, выбранный в качестве прототипа, включающий последовательное приложение к АКО, находящемуся на орбите одного небесного тела отлетного импульса V_отл и тормозного импульса V_торм для перехода на орбиту другого небесного тела с заданными параметрами по высоте и положению плоскости орбиты. Такой способ управления активным кораблем применялся при проведении лунных миссий по программе "Apollo" [2. В.И. Левантовский "Механика космического полета в элементарном изложении", Наука, Москва, 1970].

Первый отлетный импульс V_отл переводит АКО с орбиты искусственного спутника Земли (ИСЗ) на переходную орбиту по траектории отлета к Луне, обеспечивая по окончанию перелета заданное положение плоскости орбиты, определяемой наклонением i и долготой восходящего узла Ω_ВУ, а также требуемую высоту периселения. Второй тормозной импульс V_торм, выполняемый в периселении против вектора скорости, обеспечивает переход АКО на целевую орбиту искусственного спутника Луны (ИСЛ) с заданными параметрами по высоте.

Недостатком этого способа является малая вероятность попадания АКО сразу в окрестность ПКО, что потребует дополнительного времени и топлива на последующее фазирование для окончательного сближения объектов.

Техническим результатом изобретения являются сокращение продолжительности сближения с ПКО, находящемся на орбите другого небесного тела и снижение затрат топлива на сближение.

Технический результат достигается благодаря тому, что в способе управления движением АКО, стыкуемого с ПКО, включающем последовательное приложение к АКО, находящемуся на орбите одного небесного тела отлетного импульса V_отл и тормозного импульса V_торм для перехода на орбиту другого небесного тела с заданными параметрами по высоте и положению плоскости орбиты, в отличие от известного, перед переводом АКО на траекторию полета к другому небесному телу, величину и место приложения отлетного импульса V_отл определяют исходя из условия пересечения АКО орбиты ПКО при одновременном нахождении объектов в окрестности точки пересечения орбит, после чего АКО переводят на орбиту другого небесного тела путем одновременного приложения к нему тормозного импульса V_торм для обеспечения заданных параметров по высоте орбиты и бокового импульса ΔV_б для совмещения плоскостей орбит стыкующихся объектов, рассчитываемого по формуле

где V₀ - орбитальная скорость вращения ПКО вокруг другого небесного тела;

ΔΩ_ВУ - разница долгот восходящих узлов орбит стыкующихся объектов;

i - наклонение орбиты ПКО;

u - аргумент широты ПКО в точке пересечения орбит стыкующихся объектов.

Технический результат в предлагаемом способе управления достигается тем, что отлетный импульс V_отл определяется исходя из условия, что АКО и ПКО, имея рассогласование между плоскостями орбит, одновременно приходят в окрестность точки пересечения орбит в момент выполнения тормозного импульса V_торм. После одновременного приложения тормозного импульса V_торм и бокового импульса ΔV_б, угол между плоскостями орбит АКО и ПКО ликвидируется. В результате АКО оказывается в окрестности ПКО без дополнительных затрат топлива и времени на проведение фазирования и последующее сближение. Сущность изобретения поясняется фиг.1÷4 и табл.1÷2,

где на фиг.1 показана схема сближения КК, в качестве АКО с ОС, в качестве ПКО;

на фиг.2 показана схема выведения КК "Apollo-11" с околоземной орбиты на целевую окололунную орбиту;

фиг.3 показывает взаимную геометрию орбит КК и ЛОС, находящихся на полярных орбитах (i=90°) с разницей по долготе восходящего узла орбиты ΔΩ_ВУ,

фиг.4 показывает взаимную геометрию пересекающихся орбит КК и ЛОС с различным наклонением и положением восходящих узлов орбиты;

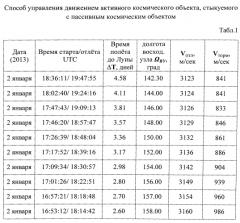
в табл.1 для гипотетического случая представлены результаты численного интегрирования плоского перелета на полярную орбиту ИСЛ с наклонением i=90°, включающие время старта с Земли и время выдачи отлетного импульса V_отл к Луне в UTC (Universal Time Coordinated), время перелета ΔT, долготу восходящего узла орбиты Ω_ВУ, величины отлетного импульса V_отл и тормозного импульса V_торм;

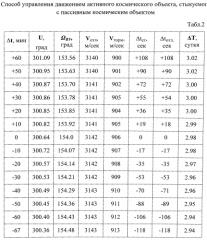
в табл.2 представлены характеристики перелетов с различным временем прихода на орбиту ИСЛ относительно номинального перелета на полярную орбиту ИСЛ с долготой восходящего узла Ω_ВУ=154°, представленного в табл.1, где Δt - относительное изменение времени прихода на орбиту ИСЛ, u - аргумент широты точки прилета, Ω_ВУ - долгота восходящего узла орбиты, величины отлетного импульса VOTJ1 и тормозного импульса V_торм, Δt_ст и Δt_отл - изменение времени старта и времени выдачи отлетного импульса V_отл по сравнению с номинальным перелетом, ΔT - время перелета к Луне.

На фиг.1 показана известная схема сближения КК с ОС. КК выводится на орбиту (поз.1), совпадающую с плоскостью орбиты ОС (поз.2) с начальным фазовым углом Ф. После проведения первого двухимпульсного маневра (V₁ и V₂) КК переходит на орбиту фазирования (поз.3), для ликвидации углового рассогласования, после чего, посредством проведения двухимпульсного маневра (V₃ и V₄), осуществляется переход КК в окрестность ОС (поз.4).

На фиг.2 показана известная схема перелета КК "Apollo-11" на орбиту ИСЛ. Вначале КК выводится (поз.1) на орбиту ИСЗ (поз.2). Первым отлетным импульсом V_отл КК переводится на переходную орбиту (поз.3) для перелета к Луне. Величина этого импульса ~3150 м/с. Длительность перелета ~3.5 дня. По достижении периселения орбиты вокруг Луны вторым тормозным импульсом V_торм (~900 м/с), направленным против скорости движения, КК переводится на орбиту ИСЛ (поз.4).

На фиг.3 представлено сферическое изображение пересекающихся полярных орбит КК (поз.1) и ЛОС (поз.2), отличающимися по долготе восходящего узла орбиты на угол ΔΩ_ВУ. В момент приложения к КК тормозного импульса V_торм и перехода на целевую орбиту (точка О′) (поз.3) ЛОС находится в точке О (поз.4) с тем же угловым расстоянием U до экватора (поз.5). Точка пересечения орбит, в которой необходимо приложить импульс для совмещения плоскостей орбит КК и ЛОС, находится на полюсе (точка С) (поз.6).

На фиг.4 представлено сферическое изображение двух пересекающихся орбит. Полярной орбите ЛОС (поз.1) с наклонением i=90° принадлежит дуга с длиной U, а орбите КК (поз.2) дуга (наклонение i₁≠90°). За счет отличия в наклонении орбиты КК и варьирования времени прилета КК в точку перехода на целевую орбиту ИСЛ, можно обеспечить одновременный приход ЛОС и КК в окрестность точки О (поз.3).

В качестве примера представлена задача сближения КК с ЛОС, находящейся на полярной орбите ИСЛ с наклонением i=90°. КК начинает полет к Луне с круговой орбиты ИСЗ высотой Н_кр=200 км и наклонением 51.6° по плоской траектории. Для определения импульсов перелета используется ограниченная круговая задача трех тел [3. "Основы теории полета космических аппаратов", под ред. Г.С. Нариманова и М.К. Тихонравова, Москва, «Машиностроение», 1972] с движением КК в поле тяготения Земли и Луны, решаемая численным интегрированием. Схема энергетически оптимального плоского перелета включает в себя два трансверсальных импульса. Первым отлетным импульсом V_отл КК переводится на переходную орбиту для перелета к Луне. Так как радиус орбиты Луны составляет около 384000 км, то для гомановского перехода на высокоэллиптическую орбиту, достигающую в апогее Луну, необходимо приложить отлетный импульс [1]

,

где µ - гравитационная постоянная Земли, r_н - радиус начальной орбиты, r_к - радиус конечной орбиты, который приблизительно равен радиусу лунной орбиты. При этом максимально возможное время перелета составляет половину периода Т орбиты перелета, где и - большая полуось орбиты перелета к Луне [1]. Через время перелета ΔT~5 суток, равное половине периода орбиты перелета, КК достигает окрестность Луны.

Согласно задаче Ламберта [1] перелет может быть совершен и за меньшее время за счет небольшого увеличения отлетного импульса V_отл. Например, превышение отлетного импульса на 50 м/с, по сравнению с минимально необходимым для гомановского перехода, приводит к достижению КК окрестности Луны за 2.5 суток [3].

Скорость КК в апогее переходной высокоэллиптической орбиты составит . При подлете к Луне основное влияние на движение КК начинает оказывать гравитационное поле Луны. Относительно Луны скорость КК V_α будет превышать местную параболическую скорость, т.е. 2-ую космическую скорость для Луны. Поэтому вторым тормозным импульсом V_торм КК переводится на орбиту ИСЛ. Величина этого импульса около 900 м/с и рассчитывается как V_торм=V_α-V₀, где V₀~1730 м/с - орбитальная скорость ИСЛ [3]. Плоский двухимпульсный перелет в любую дату обеспечивает переход на окололунную орбиту с заданным наклонением i и высотой, но при этом плоскость орбиты, определяемая долготой восходящего узла Ω_ВУ, может отличаться от плоскости целевой орбиты ЛОС. Каждый день, за счет естественного вращения Луны вокруг своей оси, достижимая долгота восходящего узла Ω_ВУ при перелете КК с Земли будет изменять свое значение на ~13.2° [3]. Таким образом, в течение лунного месяца (период 28.5 дня) появляется возможность решить задачу с плоским перелетом от Земли к Луне на орбиту ИСЛ с заданным наклонением i и временем перелета ΔT с точностью по долготе Ω_ВУ в 13-14°. Варьируя длительностью перелета ΔT в пределах ±1 день, за счет незначительного изменения величины отлетного импульса V_отл можно решить точную задачу выхода на окололунную орбиту с заданной долготой восходящего узла Ω_ВУ.

Для демонстрации сказанного, в табл.1 представлены характеристики перелета на орбиту ИСЛ с орбиты ИСЗ. Рассматривалась задача выведения КК с космодрома Байконур на круговую орбиту ИСЗ с параметрами Н_кр=200 км и наклонением i=51.6° с последующей выдачей отлетного импульса V_отл к Луне. По достижении периселения, на расстоянии 200 км от поверхности Луны к КК прикладывался тормозной импульс V_торм, переводящий КК на круговую полярную орбиту ИСЛ с наклонением i=90° и высотой орбиты Н_кр=200 км. Время перелета к Луне AT варьировалось от 4.5 суток до 2.5 суток для того, чтобы обеспечить необходимое значение долготы восходящего узла Ω_ВУ, соответствующее плоскости целевой орбиты ЛОС. Все расчеты проводились с использованием программного комплекса Satellite Tool Kit 9.0. Будем в дальнейшем изложении предполагать, что орбита ЛОС располагается в момент прилета КК в плоскости ИСЛ с Ω_ВУ=154°, что соответствует длительности перелета ΔТ=2.98 суток.

После выполнения тормозного импульса V_торм и перехода КК на орбиту ПКО необходимо проведение дополнительного фазирования, аналогичное сближению КК с ОС, так как весьма мала вероятность попадания АКО в окрестность ПКО. Это потребует дополнительного времени и топлива на последующее сближение.

Можно избежать дополнительного фазирования КК, обеспечив приход ЛОС на аргумент широты u в момент выдачи тормозного импульса V_торм для перехода КК на целевую орбиту (т.О′ фиг.3). Этот результат можно достичь незначительным варьированием времени прилета КК в периселений. В табл.2 представлены характеристики перелета относительно номинального перелета на орбиту Луны 2 января 2013 года с долготой восходящего узла Ω_ВУ=154°. Так как длительность витка на круговой лунной орбите высотой Н_кр=200 км составляет 127.5 мин, то для охвата всех возможных фазовых углов в диапазоне ±180° на момент прилета КК на целевую орбиту ЛОС в таблице представлены данные с дискретным сдвигом относительно номинального прилета КК в периселений ±10 минут.

Как видно из табл.2, максимальное значение расхождения по долготе восходящего узла орбиты КК Ω_ВУ от номинального значения Ω_ВУ для ЛОС составляет около 0.5° и может быть ликвидировано боковым импульсом ΔV_б в точках пересечения орбит стыкующихся объектов, расположенных, в случае полярной орбиты ЛОС, над полюсами Луны - т.С (см. фиг.3), что потребует дополнительно полета от точки выдачи тормозного импульса V_торм до точки пересечения около полвитка. Предельные затраты характеристической скорости на боковой импульс ΔV_б для ликвидации углового рассогласования ΔΩ_ВУ~0.5° составляют 10-12 м/с.

Чтобы сократить затраты топлива КК на проведение бокового импульса ΔV_б и время полета до стыковки предлагается совместить выполнение бокового импульса ΔV_б одновременно с тормозным импульсом V_торм. Для этого необходимо обеспечить два условия. Во-первых, точка пересечения орбиты ЛОС и переходной орбиты КК должна находиться на аргументе широты точки прилета КК в периселений, во-вторых, время прихода КК в периселений должно совпасть с временем прохождения ЛОС точки пересечения орбит (поз.4 фиг.4).

Как следует из табл.2, аргумент широты точки прилета КК соответствует u~300°, характерный для «южных» траекторий полета к Луне [3]. Первое условие предлагается выполнить за счет незначительного изменения наклонения переходной орбиты КК. В этом случае ближайшая точка пересечения орбит КК и ЛОС, в которой производится приложение тормозного импульса V_торм, переместится с полюса (поз.6 фиг.3) в поз.3 (фиг.4). Второе условие, характеризующее фазовое рассогласование, можно выполнить выбором из табл.2 соответствующего варианта сдвига по времени прилета КК в окрестность Луны.

Определим потребное значение наклонения i₁ переходной орбиты КК и предельные затраты характеристической скорости на боковой импульс ΔV. Для этого воспользуемся вариантом орбиты с прилетом КК в периселений с максимальным отклонением по долготе восходящего узла Q_By от долготы восходящего узла ЛОС, т.е. с Δt=-67 мин и u~300° (табл.2). На фиг.4 представлена точка пересечения двух орбит (ЛОС и КК) на заданном аргументе широты (т.О). Рассмотрим сферический треугольник ΔАОВ. Дуга принадлежит орбите КК с наклонением i₁. Дуга принадлежит орбите ЛОС с наклонением i=90°. По условию задачи длины этих дуг U практически одинаковы (КК и ЛОС находятся на одном аргументе широты u~300°). Дуга определяется разностью между долготами восходящих узлов ΔΩ_ВУ обеих орбит (в нашем примере ΔΩ_ВУ~0.5°). Угол i_R - угол между плоскостями.

Из решения узких сферических треугольников [4. К.А. Куликов «Курс сферической астрономии» изд. Физ-мат литературы, Москва, 1961]

sini_R·sinU=sinΔΩ_ВУ·sini

и, ввиду малости i_R и ΔΩ_ВУ

т.к. u=360°-U, то sinu=-sinU и

Так как варианту с Δt=-67 мин соответствует ΔΩ_ВУ=0.48°, то угол между плоскостями орбит КК и ЛОС составит i_R=0.55° или ~0.01 радиан.

Наклонение КК i₁ определяем, используя уравнение косинусов для сферического треугольника ΔАОВ.

cosi₁=-cosi_R·cosi+sini_R·sini·cosU

или, с учетом малости i_R

i₁=arccos(-cosi+i_R·sini·cosU).

Таким образом, потребное наклонение i₁ орбиты прилета КК в случае ЛОС на полярной орбите составит 89.73°, а величина бокового импульса

Формирование наклонения лунной орбиты и восходящего узла орбиты обеспечивается моментом выдачи и величиной отлетного импульса V_отл. Переход на окололунную орбиту обеспечивается тормозным импульсом V_торм. На фоне большого (~900 м/с) тормозного импульса V_торм [3] боковой импульс ΔV_б~17 м/с увеличит суммарный импульс на величину

Таким образом, использование предложенного способа позволяет отказаться от фазирования на орбите другого небесного тела, за счет прямого перехода в окрестность орбитальной станции и существенно сэкономит топливо КК на сближение.

Способ управления движением активного космического объекта, стыкуемого с пассивным космическим объектом, включающий последовательное приложение к активному космическому объекту, находящемуся на орбите одного небесного тела отлетного импульса V_отл и тормозного импульса V_торм для перехода на орбиту другого небесного тела с заданными параметрами по высоте и положению плоскости орбиты, отличающийся тем, что перед переводом активного космического объекта на траекторию полета к другому небесному телу, величину и место приложения отлетного импульса V_отл определяют исходя из условия пересечения активным космическим объектом орбиты пассивного космического объекта при одновременном нахождении объектов в окрестности точки пересечения орбит, после чего активный космический объект переводят на орбиту другого небесного тела путем одновременного приложения к нему тормозного импульса V_торм для обеспечения заданных параметров по высоте орбиты и бокового импульса ΔV_б для совмещения плоскостей орбит стыкующихся объектов, рассчитываемого по формуле где V₀ - орбитальная скорость вращения пассивного космического объекта вокруг другого небесного тела;ΔΩ_ВУ - разница долгот восходящих узлов орбит стыкующихся объектов;i - наклонение орбиты пассивного космического объекта;u - аргумент широты пассивного космического объекта в точке пересечения орбит стыкующихся объектов.