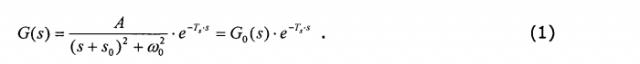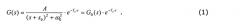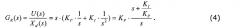Регулирующий модуль и устройство для возврата в исходное состояние осциллятора, возбуждаемого гармоническим колебанием, а также датчик мгновенной угловой скорости

Регулирующий модуль и устройство для возврата в исходное состояние осциллятора, возбуждаемого гармоническим колебанием, а также датчик мгновенной угловой скорости

Иллюстрации

Показать все

Реферат

Изобретение относится к регулирующему модулю для возврата в исходное состояние отклонения осциллятора, возбуждаемого гармоническим колебанием, к устройству, включающему в себя такой регулирующий модуль, в частности к датчику мгновенной угловой скорости, а также к способу эксплуатации и изготовления такого регулирующего модуля.

Обычные методики регулирования приспособлены к задаче регулирования с постоянной или изменяющейся лишь медленно задающей величиной, при этом значение регулируемой величины, подвергаемой влиянию возмущающей величины, удерживают в максимальной близости от заданного номинального значения или же сопровождают его в максимальной близости от изменяющегося номинального значения. Некоторые варианты применения, например микромеханические датчики мгновенной угловой скорости для определения значения кориолисовой силы, предусматривают возврат в исходное состояние отклонения осциллятора, колеблющегося в стационарных условиях со своей резонансной частотой, при помощи регулирующего контура. Регулятор для такого регулирующего контура с гармоническим колебанием в качестве задающей величины обычно рассчитывают таким образом, что возбуждающий осциллятор гармонический силовой сигнал F компенсируется так, что осциллятор по возможности не совершает перемещения, не считая гармонического колебания, соответствующего задающей величине.

Обычно эту задачу регулирования решают при помощи подхода, показанного на фиг.1A-1D. Фиг.1A относится к устройству 100, содержащему объект регулирования, например механический осциллятор 190, поступательное или вращательное отклонение которого регистрируется чувствительным элементом 170. Осциллятор 190 установлен или же подвешен таким образом, что он является подвижным вдоль направления возбуждения и может колебаться с резонансной круговой частотой ω₀. Вдоль направления возбуждения на осциллятор 190 действует гармонический силовой сигналу F_e. Выдаваемый чувствительным элементом 170 измерительный сигнал отображает перемещение осциллятора 190 вдоль направления возбуждения. Перемещение осциллятора 190 включает в себя модулированное амплитудой F силы (возмущающий сигнал) резонансное колебание с резонансной круговой частотой ω₀ осциллятора 190.

Измерительный сигнал (выходной сигнал системы) подводят к регулирующему модулю 120, содержащему демодулятор 122. В демодуляторе 122 выходной сигнал системы перемножают с гармоническим сигналом с частотой ω₀, равной резонансной круговой частоте ω₀ осциллятора 190, при этом образуются версия выходного сигнала системы в первичной полосе частот, а также дополнительные смешанные произведения. Фильтр 124 нижних частот демпфирует более высокие частотные составляющие, в частности, при двойной резонансной круговой частоте 2·ω₀ осциллятора 190. Сигнал в первичной полосе частот подводят к регулятору 126, который работает в первичной полосе частот, и для разработки и назначения параметров которого могут применяться общеупотребительные методы расчета регуляторов. Например, регулятором 126 является непрерывный пропорционально-интегральный регулятор, при помощи которого благодаря его интегральной компоненте при наличии постоянной задающей величины может быть достигнута высокая стационарная точность.

Выходной сигнал регулятора 126 перемножают (модулируют) в модуляторе 128 с гармоническим сигналом с частотой ω₀, равной резонансной круговой частоте ω₀ осциллятора 190. Результат модуляции подводят в качестве регулирующего сигнала к исполнительному органу 180, который на основании регулирующего сигнала воздействует на осциллятор 190 усилием, противодействующим отклонению осциллятора 190. При помощи резонансной круговой частоты ω₀ и демпфирования s₀ осциллятора, а также усиления А и времени T_s запаздывания системы, образованной из исполнительного органа 180, осциллятора 190 и чувствительного элемента 170, передаточная функция регулируемого осциллятора 190 может быть представлена уравнением (1):

В дальнейшем принято, что демпфирование s₀ осциллятора 190 намного меньше, чем его резонансная круговая частота, s_a<<ω₀, и что осциллятор 190 в общей сложности возбуждается гармоническим силовым сигналом F_e, при котором амплитуда F силы накладывается на колебание возбуждения с резонансной круговой частотой ω₀ осциллятора или же модулирует его по амплитуде:

При этом в соответствии с фиг.1 В исполнительный орган 180, осциллятор 190 и чувствительный элемент 170, показанные на фиг.1A, могут быть представлены в виде системы с точкой 191 суммирования и передаточной функцией G(s), при этом в точке 191 суммирования выработанный регулирующим модулем 120 регулирующий сигнал суммируется с гармоническим силовым сигналом F_e, и на суммарный сигнал воздействует передаточная функция G(s) согласно уравнению (1).

Фильтр 124 нижних частот, который уже при двойной резонансной круговой частоте осциллятора должен иметь достаточное демпфирование, чтобы в достаточной мере демпфировать смешанное произведение при 2·ω₀, ограничивает ширину полосы частот регулятора и, таким образом, его скорость реакции на изменения силовой амплитуды F.

На фиг.1C схематически показан выходной сигнал u(t) на выходе непрерывного пропорционально-интегрального регулятора с передаточной функцией G_R(s). Постоянный входной сигнал x_d(t) на входе регулятора образует пропорциональную времени кривую u(t) на выходе регулятора.

Для непрерывного пропорционально-интегрального регулятора с коэффициентом усиления K_P и коэффициентом интегрирования K_I для входного сигнала в виде скачкообразного сигнала σ(t) получается реакция u(t) на ступенчатое воздействие согласно уравнению (3):

При помощи преобразования Лапласа σ(t) и уравнения (3) получается передаточная функция G_R(s) согласно уравнению (4):

Характерным для непрерывного пропорционально-интегрального регулятора является получающийся вследствие интегрального компонента полюс при s=0. Если пропорционально-интегральный регулятор применяют в сочетании с объектом регулирования первого порядка, имеющим объектную функцию G_S(s), объектный параметр K_S и граничную круговую частоту ω₁, согласно уравнению (5)

то параметры регулятора, то есть, коэффициент усиления K_P и коэффициент интегрирования K_I обычно выбирают таким образом, что полюс объектной функции G_S(s) (объектный полюс) компенсируется посредством нулевой точки передаточной функции G_R(s) регулятора (нулевой точки регулятора). Посредством сопоставления коэффициентов в уравнениях (4) и (5) в качестве условия для параметров регулятора получается зависимость согласно уравнению (6):

Уравнение (6) устанавливает только отношение коэффициента K_P усиления к коэффициенту K_I интегрирования. Произведение передаточной функции объекта G_S(s) и передаточной функции G_R(s) регулятора дает передаточную функцию G_K(s) скорректированного открытого контура. Вследствие того, что объектный полюс согласно уравнению (5) и нулевая точка регулятора согласно уравнению (4) взаимно сокращаются, для передаточной функции G_K(s) скорректированного открытого контура получается зависимость согласно уравнению (7):

Из частотной характеристики скорректированного открытого контура при помощи критерия Найквиста может быть сделано заключение о параметрах стабильности замкнутого контура. Вследствие интегральной характеристики скорректированного открытого контура получается количественная характеристика, которая спадает с величиной 20 дБ на десятичный разряд. Для положительных частот, которыми обычно ограничено применение критерия Найквиста, фаза всегда составляет -90°. Фазовая характеристика является нелинейной функцией и при частоте, равной 0, имеет скачок на 180° от +90° для отрицательных частот до -90° для положительных частот. Передаточная функция G_W(s) для замкнутого контура получается из передаточной функции G_K(s) скорректированного открытого контура в общем случае согласно уравнению (8):

Из уравнения (8) получается, что передаточная функция G_W(s) для замкнутого контура является стабильной только тогда, когда амплитудно-фазовая характеристика скорректированного открытого контура при 0≤ω<∞ ни окружает точку -1, ни проходит через нее. Эквивалентным этому условием является то, что при прохождении количественной характеристики скорректированного открытого контура через линию 0 дБ фаза скорректированного открытого контура больше, чем -180°. Так как в упомянутом выше случае фаза постоянно составляет -90°, то в соответствии с этим замкнутый контур всегда является стабильным, независимо от выбора коэффициента K_P усиления.

Из частоты при прохождении количественной характеристики через линию 0 дБ можно сделать заключение о ширине полосы частот замкнутого контура. Посредством коэффициента К_Р усиления количественная частотная характеристика может сдвигаться в направлении ординаты и, таким образом, может оказываться влияние на прохождение через линию 0 дБ или же на получающуюся вследствие этого ширину полосы частот.

На фиг.1D показан вариант выполнения, содержащий объект регулирования первого порядка с граничной круговой частотой ω₁=2·π·100 Гц, объектным параметром K_S=ω, и содержащий пропорционально-интегральный регулятор, нулевая точка которого выбрана таким образом, что она компенсирует объектный полюс, и коэффициент K_P усиления которого равен 1. В левой колонке сверху вниз показаны количественные частотные характеристики объекта регулирования, регулятора, скорректированного открытого контура и замкнутого контура, а в правой колонке сверху вниз показаны фазово-частотные характеристики объекта регулирования, регулятора, скорректированного открытого контура и замкнутого контура. Как видно на диаграмме слева внизу, ширина полосы частот замкнутого контура, определяемая частотой, при которой количественная частотная характеристика замкнутого контура спадает на 3 дБ, составляет примерно 100 Гц.

Применение классического пропорционально-интегрального регулятора предполагает наличие относительно постоянной задающей величины, вследствие чего варианты применения, в которых подлежит доведению до минимума гармоническая задающая величина с почти неизменной частотой, предполагают применение демодулятора и включенного за ним фильтра нижних частот, которые из гармонического входного сигнала вырабатывают соответствующий сигнал в первичной полосе частот.

Задачей изобретения является предложить улучшенную концепцию регулятора для возврата в исходное состояние вызванного возмущающей величиной отклонения осцилляторов, гармонически колеблющихся в стационарном случае, например, одного из подвижно установленных модулей датчика мгновенной угловой скорости. Задача решена при помощи предмета независимых пунктов формулы изобретения. Предпочтительные усовершенствования вытекают из соответствующих зависимых пунктов формулы изобретения.

Ниже при помощи чертежей описаны варианты выполнения изобретения, принцип их функционирования, а также их преимущества. Элементы вариантов выполнения могут комбинироваться друг с другом, если только они друг друга не исключают.

На фиг.1A показана блок-схема известного по состоянию техники устройства, содержащего гармонически возбуждаемый осциллятор и регулирующий модуль для возврата в исходное состояние отклонения осциллятора.

На фиг.1B показана схематическая модель устройства согласно фиг.1A.

На фиг.1C иллюстрируется передаточная функция непрерывного пропорционально-интегрального регулятора, работающего в первичной полосе частот.

На фиг.1D показаны диаграммы частотных характеристик непрерывного пропорционально-интегрального регулятора для иллюстрации принципа действия регулирующих модулей, известных по состоянию техники.

На фиг.2A показана блок-схема устройства, содержащего регулирующий модуль согласно варианту выполнения, который относится к регулирующему модулю, содержащему непрерывный пропорционально-интегральный регулятор для гармонических задающих величин и звено с запаздыванием.

На фиг.2B схематически показана передаточная функция пропорционально-интегрального регулятора согласно фиг.2A.

На фиг.2C показаны схематические диаграммы частотных характеристик для регулирующего модуля, представленного на фиг.2A.

На фиг.3A показана блок-схема устройства, содержащего регулирующий модуль согласно варианту выполнения, который относится к регулирующему модулю, содержащему дискретный пропорционально-интегральный регулятор для гармонических задающих величин и звено с запаздыванием.

На фиг.3B схематически иллюстрируется передаточная функция регулирующего модуля согласно фиг.3A.

На фиг.3C показаны схематические диаграммы частотных характеристик для пояснения принципа действия регулирующего модуля, представленного на фиг.3A.

На фиг.3D показана упрощенная блок-схема трансформированного в первичную полосу частот регулирующего модуля согласно фиг.3A в соответствии с одним вариантом выполнения.

На фиг.3E показаны схематические диаграммы частотных характеристик дискретного регулирующего модуля, параметры которого назначены согласно одному варианту выполнения способа изготовления регулирующего модуля, включающего в себя определение параметров регулятора путем задания собственных значений.

На фиг.4A показана блок-схема устройства, содержащего регулирующий модуль согласно варианту выполнения, который относится к регулирующему модулю, содержащему дискретный пропорционально-интегральный регулятор для гармонических задающих величин и дополнение регулятора, действующее аналогично полосовому фильтру.

На фиг.4B схематически показана передаточная функция дополнения регулятора согласно фиг.4A.

На фиг.4C показаны диаграммы частотных характеристик для пояснения принципа действия дополнения регулятора согласно фиг.4A.

На фиг.5A показан схематический вид сверху микромеханической части датчика мгновенной угловой скорости согласно следующему варианту выполнения изобретения.

На фиг.5B показано схематическое изображение в поперечном сечении микромеханической части датчика мгновенной угловой скорости согласно фиг.5A.

На фиг.5C показана блок-схема датчика мгновенной угловой скорости согласно фиг.5A и 5B.

На фиг.6 показан схематический вид сверху микромеханической части датчика мгновенной угловой скорости согласно следующему варианту выполнения изобретения.

На фиг.7A показана упрощенная структурная схема способа эксплуатации датчика мгновенной угловой скорости.

На фиг.7B показана упрощенная структурная схема способа изготовления датчика мгновенной угловой скорости.

Вариант выполнения, показанный на фиг.2A, относится к устройству 200, содержащему регулирующий модуль 220, который включает в себя пропорционально-интегральный регулятор 225 для гармонических задающих величин, содержащий интегрирующее передаточное звено 222 с коэффициентом K_I интегрирования и пропорциональное передаточное звено 224 с коэффициентом K_P усиления. Пропорционально-интегральный регулятор 225 для гармонических задающих величин вырабатывает из модулированного по амплитуде скачкообразной функцией гармонического колебания с постоянной амплитудой на входе регулятора гармоническое колебание с такой же частотой и пропорциональной времени амплитудой на выходе регулятора.

На фиг.2B иллюстрируется преобразование синусно модулированного скачкообразного сигнала x_d(t) в гармонический выходной сигнал u(t) с пропорциональной времени амплитудой посредством передаточной функции G_R0(s) пропорционально-интегрального регулятора 225. Описанный режим пропорционально-интегрального регулятора предполагает назначение параметров K₁, K_P регулятора, которое описано ниже.

Аналогично уравнению (3) уравнение (9) воспроизводит зависимость между выходным сигналом u(t) регулятора и входным сигналом x_d(t) регулятора для x_d(t)=σ(t):

Преобразования Лапласа выходного сигнала u(t) регулятора и входного сигнала x_d(t) регулятора получаются из уравнений (9а) и (9b):

В соответствии с этим, передаточная функция G_R0(s) пропорционально-интегрального регулятора 225 для гармонических задающих величин получается согласно уравнению (10):

Характерным для непрерывного пропорционально-интегрального регулятора 225 является получающийся вследствие обобщенной интегральной компоненты комплексно сопряженный полюс при s=±jω₀.

При гармоническом колебании с частотой ω₀ на входе регулятора пропорционально-интегральный регулятор 225 не образует на выходе регулятора смещение фазы. Поэтому для установления произвольной фазы регулирующий модуль 220 дополнительно включает в себя звено 226 с запаздыванием, имеющее время T_R запаздывания, включенное последовательно с пропорционально-интегральным регулятором 225. В соответствии с этим передаточная функция G_R(s) регулирующего модуля 220 получается согласно уравнению (11):

Параметры K_I, K_P регулятора выбирают таким образом, что нулевые точки регулятора в передаточной функции регулятора согласно уравнению (11) компенсируют комплексно сопряженный объектный полюс в передаточной функции объекта согласно уравнению (1). Посредством сопоставления коэффициентов в уравнениях (1) и (11) для определения параметров K_I, К_Р регулятора получаются уравнения (12а) и (12b):

Согласно одному варианту выполнения демпфирование s₀ и резонансную круговую частоту ω₀ осциллятора 190 выбирают таким образом, что s₀<<ω₀, и таким образом, уравнение (12b) выполнено с очень хорошим приближением. Из уравнения (12а) получается уравнение (12с), служащее в качестве условия назначения отношения коэффициента K_I интегрирования к коэффициенту К_Р усиления:

Передаточная функция G_K(s) скорректированного открытого контура получается из произведения передаточной функции G_S(s) объекта и передаточной функции G_R(s) регулятора. Так как при соответствующем назначении параметров согласно уравнениям (12b), (12с) выражения для комплексно сопряженного объектного полюса и комплексно сопряженной нулевой точки регулятора сокращаются, получается передаточная функция G_K(s) скорректированного открытого контура согласно уравнению (13):

При регулировании с помощью традиционного пропорционально-интегрального регулятора в фазово-частотной характеристике скорректированного открытого контура при частоте ω=0 происходит скачок фазы с +90° на -90°. В противоположность этому, в рассчитанном для гармонических задающих величин пропорционально-интегральном регуляторе 255 при частоте ω₀ происходит скачок фазы на 180°, который однако не обязательно осуществляется между значениями +90° и -90°. Поэтому согласно одному варианту выполнения время TR запаздывания регулятора выбирают таким образом, что скачок фазы на 180° происходит по возможности точно при ω₀, например, посредством того, что параметры регулятора назначают согласно уравнению (14а):

Если смещение фазы при ω₀, вызванное одним только временем T_S запаздывания объекта, меньше 90°, то можно также образовать фазовую компоненту в размере 180° при помощи инвертирующего регулятора. В этом случае фазы, вызванные временем T_R запаздывания регулятора и временем T_S запаздывания объекта, при ω₀ должны лишь дополняться до π 2 . При этом условие для назначения времени T_R запаздывания регулятора имеет вид:

Из частотной характеристики скорректированного открытого контура при помощи критерия Найквиста можно сделать заключение о параметрах стабильности замкнутого контура. Скорректированный открытый контур состоит из обобщенного интегратора и комбинации времени T_S запаздывания объекта и времени T_R запаздывания регулятора. Благодаря надлежащему назначению времени T_R запаздывания регулятора согласно одному из уравнений (14a) или (14b) фазовая характеристика при частоте а>0 имеет скачок на 180° от +90° для более низких частот ω<ω₀ до -90° для более высоких частот ω>ω₀. Передаточная функция G_W(s) замкнутого контура снова получается из передаточной функции G_K(s) скорректированного открытого контура согласно уравнению (8):

Если время T_R запаздывания регулятора определяют согласно уравнению (14a), то замкнутый контур является стабильным именно тогда, когда амплитудно-фазовая характеристика скорректированного открытого контура при 0≤ω<ω₀ ни окружает точку -1, ни проходит через нее.

Если, в противоположность этому, время T_R запаздывания регулятора определяют при помощи уравнения (14b), и пропорционально-интегральный регулятор 225 вырабатывает фазу в размере 180°, то замкнутый контур является стабильным именно тогда, когда амплитудно-фазовая характеристика скорректированного открытого контура начинается на отрицательной вещественной оси при значении, большем -1.

В интервале 0≤ω<ω₀ количественная характеристика пересекает линию 0 дБ при частоте прохождения, при этом частотный интервал частоты прохождения по отношению к ω₀ определяет ширину полосы частот замкнутого контура. Посредством коэффициента K_P усиления количественная частотная характеристика и, таким образом, частота прохождения, могут сдвигаться в направлении ординаты, так что образующаяся ширина полосы частот для замкнутого контура может регулироваться. Согласно одному варианту выполнения коэффициент K_P усиления выбирают в рамках границ, заданных критериями стабильности, таким образом, что ширина полосы частот является максимальной.

На фиг.2C в левой колонке сверху вниз показаны количественные частотные характеристики регулируемого объекта, регулятора, скорректированного открытого контура, а также замкнутого контура, а в правой колонке показаны фазово-частотные характеристики объекта регулирования, регулятора, скорректированного открытого контура и замкнутого контура для варианта выполнения, при котором применены следующие параметры объекта регулирования:

резонансная круговая частота осциллятора ω₀=2·π·9000 Гц,

демпфирование осциллятора s 0 = π 200000 ,

усиление A = s 0 2 + ω 0 2 , и

время запаздывания объекта T s = π 4 ⋅ ω 0 .

Нулевая точка регулятора выбрана таким образом, что компенсируется объектный полюс. Так как вызванная временем запаздывания объекта фаза при ω₀ меньше 90°, то фазовая компонента в размере 180° может быть реализована при помощи отрицательного знака в регуляторе (инвертирующий регулятор). Для коэффициента усиления K P = − 1 10 получаются коэффициент K_I интегрирования согласно уравнению (12c) и время T_R запаздывания регулятора согласно уравнению (14b) в размере T R = π 4 ⋅ ω 0 .

Образующаяся ширина полосы частот замкнутого контура составляет примерно 500 Гц и является существенно большей, чем в сравнительном варианте выполнения для традиционного пропорционально-интегрального регулятора, работающего в первичной полосе частот.

Показанное на фиг.2A устройство 200 включает в себя осциллятор 190 и регулирующий модуль 220. Осциллятором 190 является масса, которая является подвижной вдоль направления возбуждения и может колебаться вдоль него с резонансной круговой частотой ω₀. В стационарном случае, то есть, без воздействия возмущающей величины, осциллятор 190 совершает поступательное или вращательное колебание с резонансной круговой частотой ω₀. На это колебание накладывается отклонение, вызванное силовой амплитудой F. Чувствительный элемент 170 регистрирует перемещение осциллятора 190 и выдает измерительный сигнал, который отображает общее отклонение осциллятора 190 вдоль направления возбуждения. Измерительный сигнал соответствует входному сигналу регулятора для регулирующего модуля 220. Регулирующий модуль 220 вырабатывает из входного сигнала регулятора выходной сигнал регулятора и выдает его на исполнительный орган 180. Исполнительный орган 180 противодействует вызванному силовым сигналом F отклонению осциллятора или же его компенсирует, так что осциллятор 190 совершает гармоническое колебание с постоянной амплитудой и с резонансной круговой частотой ω₀.

Регулирующий модуль 220 содержит пропорционально-интегральный регулятор 225 для гармонических задающих величин, который включает в себя пропорциональное передаточное звено 224 с коэффициентом K_P усиления и интегрирующее передаточное звено 222 с коэффициентом K_I интегрирования. Коэффициент K_I интегрирования и коэффициент K_P усиления выбраны таким образом, что в плоскости s нулевая точка передаточной функции пропорционально-интегрального регулятора 225 и комплексно сопряженный полюс передаточной функции объекта, описывающей осциллятор 190, взаимно компенсируются.

Согласно одному варианту выполнения демпфирование s₀ осциллятора в отношении отклонения в направлении возбуждения намного меньше, чем резонансная круговая частота ω₀ осциллятора 190, и отношение коэффициента K_I интегрирования к коэффициенту K_P усиления в с^-1 примерно соответствует демпфированию s₀. Кроме того, коэффициент K_P усиления может выбираться таким, что образующаяся ширина полосы частот является максимально большой для соответствующих требований стабильности. При этом коэффициент K_I интегрирования выбирают в зависимости от демпфирования s₀ и коэффициента К_Р усиления согласно уравнению (12c).

Согласно одному варианту выполнения система, образованная из исполнительного органа 180, осциллятора 190 и чувствительного элемента 170, имеет время T_S запаздывания объекта, а регулирующий модуль 220 содержит действующее последовательно с пропорционально-интегральным регулятором 225 звено 226 с запаздыванием, имеющее время T_R запаздывания регулятора. Время T_R запаздывания регулятора выбирают в зависимости от резонансной круговой частоты ω₀ осциллятора 290 и времени T_S запаздывания объекта таким образом, что фазово-частотная характеристика скорректированного открытого контура при частоте ω₀ имеет фазовый скачок от +90° до -90° при повышении частоты.

Согласно первому варианту этой формы выполнения пропорционально-интегральный регулятор для гармонических задающих величин не обращает знак, а время T_R запаздывания регулятора выбирают таким образом, что произведение резонансной круговой частоты ω₀ и суммы времени T_S запаздывания объекта и времени T_R запаздывания регулятора дает в результате 3 ⋅ π 2 . Согласно другому варианту этой формы выполнения пропорционально-интегральный регулятор 225 инвертирует знак, или же сдвигает фазу на 180°, и вызванную при резонансной круговой частоте ω₀ временем T_R запаздывания регулятора и временем T_S запаздывания объекта фазу лишь дополняют до величины π 2 , так что произведение резонансной круговой частоты ω₀ и суммы времени T_S запаздывания объекта и времени T_R запаздывания регулятора дает в результате π 2 .

Так как в регулирующем модуле 220 не предусмотрено преобразование первичной полосы частот, которое требует фильтра нижних частот для демпфирования высокочастотных смешанных произведений, регулирующий модуль 220 может быть выполнен значительно более широкополосным. Регулирующий модуль 220 реагирует на возмущающие величины быстрее, чем сравнимые регуляторы, в которых предусмотрено преобразование первичной полосы частот.

Фиг.3А-3Е относятся к варианту выполнения, в котором регулирующий модуль 220 имеет дискретный пропорционально-интегральный регулятор 325 для гармонических задающих величин, содержащий дискретное пропорциональное передаточное звено 324 с коэффициентом K_P усиления и дискретное интегрирующее передаточное звено 322 с коэффициентом K_I, интегрирования. Согласно одному варианту выполнения аналоговый измерительный сигнал от чувствительного элемента 170 дискретизируют при помощи модуля 321 дискретизации с периодом Т дискретизации и преобразуют в цифровой входной сигнал для дискретного пропорционально-интегрального регулятора 325. Согласно другому варианту выполнения чувствительный элемент 170 уже выдает цифровой измерительный сигнал.

Согласно одному варианту выполнения, при котором система, включающая в себя исполнительный орган 180, осциллятор 190 и чувствительный элемент 170, имеет время T_S запаздывания объекта, регулирующий модуль 220 содержит расположенное последовательно с дискретным пропорционально-интегральным регулятором 325 звено 326 с запаздыванием, имеющее время T_R запаздывания регулятора. Ниже как время T_S запаздывания объекта, так и время T_R запаздывания регулятора выражены согласно уравнениям (16a) и (16b) в виде кратного периода Т дискретизации:

При этом время T_R запаздывания регулятора определяют таким образом, что скорректированный открытый контур при резонансной круговой частоте ω₀ имеет фазовый скачок от +90° до -90° при повышении частоты.

Согласно одному варианту выполнения отношение коэффициента K_I интегрирования к коэффициенту K_P усиления установлено таким образом, что в плоскости s нулевые точки передаточной функции регулятора компенсируют комплексно сопряженный объектный полюс передаточной функции объекта. Согласно другому варианту выполнения параметры регулятора выбраны таким образом, что передаточная функция замкнутого контура эквивалентной системы с первичной полосой частот имеет двойное вещественное собственное значение. Регулирующий модуль 220 реализован, например, в виде цифровой коммутационной схемы, в частности в виде ASIC (специализированная интегрированная коммутационная схема), DSP (цифровой процессор сигналов) или FPGA (программируемая логическая матрица).

Фиг.3B иллюстрирует передаточную функцию G_R0(z) дискретного пропорционально-интегрального регулятора 325 для гармонических задающих величин согласно фиг.3A. Передаточную функцию G_R0(z) определяют таким образом, что пропорционально-интегральный регулятор 325 из входного сигнала x_d(k), включающего в себя гармоническое колебание, модулированное скачкообразной функцией σ(k), вырабатывает в качестве выходного сигнала u(k) регулятора гармоническое колебание с такой же частотой и с пропорциональной времени амплитудой, как это выражено уравнением (17):

Входная функция X_d(z) и выходная функция U(z) получаются посредством z-преобразования согласно уравнениям (18a) и (18b):

При этом передаточная функция G_R0(z) дискретного пропорционально-интегрального регулятора 325 для гармонических задающих величин получается согласно уравнению (18c):

Вследствие обобщенной интегральной компоненты такой дискретный пропорционально-интегральный регулятор имеет полюс при z = e ± j ⋅ ω 0 ⋅ T и при гармоническом колебании с частотой ω₀ на входе не образует смещения фазы на выходе. Чтобы несмотря на это иметь возможность установления произвольной фазы, согласно одному варианту выполнения предусмотрен регулирующий модуль 220, содержащий звено 326 с запаздыванием, имеющее задержку β_D. При этом передаточная функция G_R(z) регулирующего модуля 220, содержащего звено 326 с запаздыванием и дискретный пропорционально-интегральный регулятор 325, получается согласно уравнению (19):

Модель непрерывного объекта регулирования согласно уравнению (1) должна быть соответствующим способом подвергнута дискретизации. Для этого вначале в передаточной функции G(s) объекта регулирования согласно уравнению (1) выражают время T_S запаздывания объекта согласно уравнению (16a) в виде кратного периода Т дискретизации:

В общем случае ступенчатая передаточная функция G(z) для дискретизированной модели непрерывного объекта регулирования с передаточной функцией G(s) может быть рассчитана согласно уравнению (21):

С последующими сокращениями согласно уравнениям (21а)-(21е):

из уравнений (20) и (21) получается ступенчатая передаточная функция G(z) для осциллятора 190 согласно уравнению (22):

Согласно одному варианту выполнения изобретения время T_R запаздывания регулятора определяют таким образом, что фазово-частотная характеристика скорректированного открытого контура имеет при резонансной круговой частоте ω₀ фазовый скачок с +90° до -90° при повышении частоты. Z-передаточная функция скорректированного открытого контура получается аналогично уравнению (13) из произведения передаточной функции G(z) объекта согласно уравнению (20) и передаточной функции G_R(z) регулятора согласно уравн