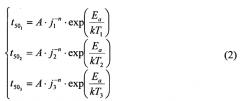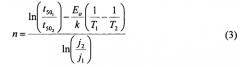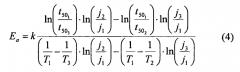Способ оценки электромиграционных параметров металлических проводников

Способ оценки электромиграционных параметров металлических проводников

Иллюстрации

Показать все

Реферат

Изобретение относится к области микроэлектроники и может быть использовано для оценки и контроля надежности металлизации, а именно металлической разводки, при производстве интегральных микросхем для оптимизации процесса производства и повышения информативности.

Прогнозирование надежности металлических проводников интегральных схем производится на основе энергии активации Е_а и показателя экспоненты n в соответствии с формулой Блэка (1), и определение данных параметров является первоочередной задачей при разработке высоконадежных металлических проводников.

Известен способ вычисления параметров Е_а и n из патента (ЕР 1978371 A, G01R 31/28, 2008). Метод основан на том, что величина энергии активации влияет на значение медианного времени наработки до отказа (median time to failure) в процессе электромиграции. Вычисление значений Е_а и n осуществляется после проведения ускоренного электромиграционного испытания металлических проводников, состоящего из трех этапов, каждый из которых отличается значением повышенной температуры и/или плотностью электрического тока. Величину энергии активации находят из наклона прямой на графике Аррениуса. Недостатками данной методики являются: во-первых, сложность переходных процессов при переключении с одного режима измерения на другой, во-вторых, использование нагревательных печей для поддержания постоянной повышенной температуры образцов, в-третьих, большая длительность испытаний (>120 ч).

Также существует методика, представленная в стандарте EIA/JEDEC JESD61, которая включает в себя проведение ускоренных электромиграционных испытаний при постоянной температуре в режиме постоянной мощности протекающего тока, при этом нагревание производится только за счет протекания тока. Критерием выхода из строя и окончания измерений служит увеличение сопротивления металлического проводника относительно начального значения, полученного в начале измерений (рекомендуемые значения - увеличение от 5% до 20%) (US 20030080761 A1, G01R 31/26, 2003). Недостатком данного метода является то, что мы получаем только медианное время отказа металлических проводников при постоянной температуре, без определения электромиграционных параметров.

Наиболее близкой к заявленному способу является методика, представленная в стандарте EIA/JEDEC JESD63, где для вычисления энергии активации определяют значения среднего времени наработки до отказа (t₅₀), по крайней мере, при трех различных значениях температуры, когда поддерживается постоянная плотность тока. В этом случае значение Е_а находят из наклона прямой, где по оси ординат откладывается ln(t₅₀), а по оси абсцисс - 1/Т (Т - температура). Для вычисления показателя степени плотности тока n, в свою очередь, определяют значения среднего времени наработки до отказа (t₅₀), по крайней мере, при трех различных значениях плотности тока, когда поддерживается постоянная температура. В таком случае значение n находят из наклона прямой, где по оси ординат откладывается ln(t₅₀), а по оси абсцисс - ln(J) (J - плотность электрического тока). Недостатками данной методики являются: во-первых, использование нагревательных печей для поддержания постоянной повышенной температуры образцов, во-вторых, через тестовые структуры пропускают токи относительно небольшой плотности (<2 МА/см²), чтобы избежать эффекта саморазогрева, что, таким образом, приводит к значительному увеличению времени испытаний (>2-4 недель).

В основу изобретения положена задача - разработать экспресс-метод, обеспечивающий возможность определить электромиграционные параметры - энергию активации Е_а и показатель степени плотности тока n, которые необходимы при оценке надежности металлических проводников.

Суть методики состоит в следующем. Электромиграционные параметры определяются на основе эмпирически полученного уравнения Блэка (J.R.Black):

где t₅₀ - медианное время наработки до отказа (median-time-to-failure) (сек), А - постоянная, j - плотность тока (А/см²), n - показатель степени плотности тока, Е_а - энергия активации (эВ), k - постоянная Больцмана (эВ/К); Т - температура (K).

Для определения значений t₅₀ проводят электромиграционные испытания при постоянной температуре, в которых нагрев образцов осуществляется за счет саморазогрева протекающим током. На Рис. 1 показана характерная зависимость сопротивления проводника от времени при проведении испытаний, состоящая из 3 областей: выход на режим испытаний, проведение измерений, выход проводника из строя.

В связи с тем, что при проведении испытаний значение температуры проводника (Т) задается при помощи саморазогрева протекающим током (j), то изменение значения температуры приведет к изменению и величины j, поэтому для определения остальных параметров (А,n,Е_а) достаточно использовать три условия для измерений: (j₁;T₁), (j₂;T₂), (j₃;Т₃). В итоге получаем систему уравнений с тремя неизвестными:

Разделив первое уравнение в системе на второе, и взяв натуральный логарифм от обеих частей, получим выражения для n:

Разделив первое уравнение на третье в системе (2) и подставив в него полученное выражение для n (3), предварительно взяв натуральный логарифм от обеих частей, получаем выражение для Е_а.

Значение коэффициента А можно определить из любого уравнения системы (2) при использовании найденных значений n и Е_а, например:

Плотность тока j₁ (i=1,2,3) для каждого значения t_50i определяется как медиана задаваемых значений плотностей тока для каждого значения температуры T_i.

Пример использования методики

В разработанной методике испытания на надежность (электромиграционные испытания) проводились на металлических проводниках с пассивирующим слоем SiO₂ толщиной 0.9 мкм. Вид тестовой структуры представлен на Рис. 2. Электромиграционные испытания проводились на группе из трех пластин. Общее число образцов было разделено на три части, для каждой из которых было установлено значение эффективной температуры испытаний (Таблица 1).

Таблица 1
Исходные данные измерений.
Структура	Топологическая длина (L), мкм	Топологическая ширина (W), мкм	Толщина (Н), мкм	Температура, °С
TiN/AlSi/TiN	800	1.2	0.7	270/300/350

Величина постоянной температуры подбиралась таким образом, чтобы время испытаний было меньше 40 мин. При испытаниях использовался измерительный стенд на базе прецизионного анализатора полупроводниковых параметров Agilent 4156C (Рис. 3). Критерием отказа и окончания измерений служило 0,5 увеличение сопротивления.

Плотность тока для металлического проводника рассчитывается по формуле

где j - плотность тока (мА/мкм²), I - величина электрического тока (мА), S - поперечное сечение проводника (мкм²), W - ширина проводника (мкм), Н - высота проводника (мкм). Значения W и Н берутся из таблицы 1.

Для получения достоверных данных, в расчетах необходимо учитывать отклонение геометрических размеров металлического проводника от номинального значения, возникающее в ходе процесса его формирования.

В данном случае учитывалось отклонение ширины металлического проводника (Рис. 4), поэтому формулу (6) для расчета плотности тока можно переписать в следующем виде

где j - плотность тока (мА/мкм), I - величина электрического тока (мА), S_offset - поперечное сечение проводника с учетом отклонения по ширине (мкм²), W - номинальная ширина проводника (мкм), W_offset - отклонение ширины проводника от номинального значения (мкм), Н - высота проводника (мкм).

Поверхностное сопротивление проводника определяется по формуле

где R - электрическое сопротивление (Ом), W - ширина проводника (мкм), W_offset - отклонение ширины проводника от номинального значения (мкм), L - длина проводника (мкм).

Для расчета W_offset используются две тестовые структуры с размерами W₁, L₁ и W₂, L₂ для расчета W_offset и сопротивлениями R₁, R₂. Тогда для двух структур в одном слое металлизации имеем

Из формулы (9) получаем отклонение ширины проводника от номинального значения

В данном случае отклонение ширины Wo_ffset прямо определялось на структуре, используемой для испытаний (см. Табл. 2).

Таблица 2
Топологические размеры проводников для определения отклонения их ширины от номинального значения.
Структура	L, мкм	W, мкм
Тест 1	800	1.2
Тест 2	800	3.6

Для определения значений электромиграционных параметров использовался следующий алгоритм:

1) Проведение цикла электромиграционных испытаний при постоянной температуре для группы образцов (Рис.5) с фиксацией времени измерения и значения электрического сопротивления через определенные промежутки времени (Δt=200-300 мсек). Испытания проводятся, по крайней мере, при трех различных значениях температур - T_test=(Т₁;Т₂;Т₃).

2) Определение значения 150 и медианы плотности тока j (Формула 7) для каждого из значений выбранных температур - ( t 50 1 ; j 1 ) , ( t 50 2 ; j 2 ) , ( t 50 3 ; j 3 ) .

3) Расчет Е_а (Формула 4).

4) Расчет n (Формула 3).

5) Расчет коэффициента А (Формула 5).

На Рис.6-8 представлены распределения измеренных времен наработки на отказ структур для каждой температуры испытаний. Проведена линейная экстраполяция результатов методом наименьших квадратов. По горизонтальной оси Х отложены времена отказов структур в логарифмическом масштабе (сек), по вертикальной оси Y-р - доля числа отказов. Линия экстраполяции имеет выражение Z=(ln t-ln t₅₀))/S, где величина Z, удовлетворяющая уравнению F₀(Z)=p, где F₀ - стандартная нормированная функция нормального распределения. Для практических расчетов в MS Excel имеется встроенная функция NORMSINV, вычисляющая по значению р величину Z в уравнении F₀(Z)=p.

Необходимо заметить, что при р=0.5 (число отказов равно 50%) функция F₀(Z=0) равна 0,5. Также пересечение линии экстраполяции с горизонтальной осью Х есть медианное время отказов 150.

В таблицах 3-5 представлены значения электрических токов (I), отклонение ширины от номинального значения (W_offset) для каждого проводника, а также рассчитанная величина плотности тока (j) (по формуле 7). Значение W_offset определялось путем электрических измерений на сформированных рядом структурах.

Таблица 3
Данные электромиграционных измерений, Т=270°С.
I, мА	Woffset, мкм	j, мА/мкм2
86.65	0.122	114.83
90.75	0.059	113.62
85.84	0.089	110.38
89.67	0.016	108.19
89.82	0.036	110.24
88.84	0.036	109.03
91.44	0.057	114.29
85.29	0.107	111.48
87.51	0.059	109.57
86.87	0.122	115.12
86.28	0.036	105.89
86.19	0.096	111.53
89.05	0.061	111.69
90.17	0.016	108.80
88.28	0.025	107.33
89.94	0.024	109.26
87.72	0.061	110.02
87.01	0.114	114.46
85.13	0.096	110.16
85.63	0.024	104.02
90.74	0.025	110.32
88.25	0.057	110.30
88.47	0.036	108.58
84.40	0.12	111.64
84.34	0.14	113.67

Таблица 4
Данные электромиграционных измерений, Т=300°C.
I, мА	Woffset, мкм	j, мА/мкм2
95.01	0.045	117.51
94.62	0.058	118.36
88.67	0.13	118.38
88.98	0.138	119.69

86.44	0.138	116.28
93.25	0.048	115.64
84.69	0.168	117.23
87.33	0.082	111.59
96.66	0.008	115.84
85.71	0.134	114.86
92.73	0.014	111.70
91.76	0.058	114.79
88.12	0.082	112.60
87.93	0.074	111.56
90.11	0.071	114.02
94.40	0.074	119.77
87.93	0.116	115.88
87.87	0.071	111.19
89.44	0.048	110.91
87.46	0.151	119.11
90.21	0.082	115.27
84.22	0.14	113.50

Таблица 5
Данные электромиграционных измерений, Т=350°C.
I, мА	Woffset, мкм	j, мА/мкм2
99.02	0.075	125.74
93.13	0.045	115.19
91.38	0.111	119.87
89.76	0.176	125.22
92.68	0.119	122.48
92.79	0.146	125.77
88.05	0.129	117.45
97.77	0.061	122.63
98.40	0.074	124.84
96.61	0.019	116.86
95.73	0.074	121.45
90.39	0.114	118.90
87.23	0.087	111.96
92.00	0.165	126.98
93.87	0.075	119.20
95.43	0.061	119.69
89.94	0.131	120.19
89.46	0.193	126.91
90.9	0.198	129.60
90.49	0.086	116.04
94.34	0.143	127.50
89.81	0.082	114.76

92.06	0.082	117.63
85.36	0.114	112.29
97.42	0.019	117.84
97.39	0.05	120.98
95.92	0.143	129.64
93.86	0.142	126.74

Таблица 6
Суммарные данные электромиграционных испытаний для трех температур испытаний.
Параметр испытаний	Т=270°C	T=300°C	Т=350°C
медианное время испытаний t50, сек	223.5	114.3	45.82
медиана значений плотностей тока j при испытании, мА/мкм2	110.3	115.45	120.59

Из формул (7)-(9) получаем: Е_а=0.492 эВ, n=2.6385, А=1.338·10²³ ч.

Наблюдаемые времена наработки до отказа металлических проводников при ускоренных испытаниях намного меньше, чем продолжительность их функционирования в рабочих условиях. Оценка времен жизни проводников в реальных условиях производится при знании рабочей температуры и тока их эксплуатации на основе формулы (1) при знании полученных параметров: энергии активации Е_а и показателя степени плотности тока n. Результаты, полученные в данной работе, могут быть использованы как для построения теоретических моделей, так и для определения электромиграционных параметров проводников с различными свойствами.

Приложение:

Определен температурный коэффициент сопротивления ТКС металлического проводника, который равен 0.00351°C^-1. Коэффициент ТКС рассчитан на основе линейной зависимости сопротивления металлического проводника от R(T) температуры Т в диапазоне 30°C, 45°C, 60°C, 90°C, 110°C:

где R₀ - сопротивление проводника при комнатной температуре Т₀=25°C. Подаваемый ток для измерения сопротивления был небольшим (20 мкА) для предотвращения теплового самонагрева из-за протекания тока.

Стандарты:

JESD63 «Standard method for calculating the electromigration model parameters for current density and temperature», EIA/JEDEC Standard, February 1998.

JESD61 «Isothermal electromigration test procedure», EIA/JEDEC Standard, April 1997.

JESD33B «Standard method for measuring and using the temperature coefficient of resistance to determine the temperature of a metallization line», EIA/JEDEC Standard, 2004.

Статьи:

Black, J.R. «Electromigration - A brief survey and some recent results», IEEE Transactions on electron devices», ED-16, 4, April 1969.

Black, J. R., «Current Limitations of Thin Film Conductors», Proceedings of the International Reliability Physics Symposium, 1982, pp. 300-306. IEEE Catalog No. 82CH17227-7.

Oates A. S. «Current density dependence of electromigration failure of submicron width, multilayer Al alloy conductors», Appl. Phys. Lett. 66, 1475 (1995).

Kononenko О.V., Matveev V.N., Field D.P., «The Energy of Activation of Electromigration in Aluminum Conductors Tested by the Drift-Velocity Method, Russian Microelectronics, Vol. 29, No. 5, 2000, pp. 316-323.

Патенты:

Патент ЕР 1978371А, класс G01R 31/28, "Electromigration testing and evaluation apparatus and methods", 2008.

Патент US 2003/0080761 A1, класс G01R 31/26, "Method and apparatus for accelerated determination of electromigration characteristics of semiconductor wiring", 2003.

Патент US 6,350,626 B1, класс H01L 21/66, "Method of testing electromigration lifetime", 2002.

Патент US 7,660,693 B2, класс G06F 3/01, "Activation energy measurement method", 2010.

Способ оценки электромиграционных параметров, состоящий в проведении испытаний металлических проводников интегральных схем при трех различных температурах T₁, T₂ и Т₃, отличающийся тем, что с целью сокращения времени испытаний и повышения информативности, нагрев металлических проводников проводится только за счет саморазогрева протекающим электрическим током с последующим расчетом электромиграционных параметров: энергии активации показателя плотности тока n = { ln ( t 50 1 / t 50 2 ) − E a ⋅ ( 1 / T 1 − 1 / T 2 ) / k } / ln ( j 2 / j 1 ) иэлектромиграционной константы металлических проводников A = t 50 1 ⋅ j 1 n / exp ( E a / ( k ⋅ T 1 ) ) , где ( t 50 1 ; j 1 ) , ( t 50 2 ; j 2 ) , ( t 50 3 ; j 3 ) - медианное время наработки на отказ металлических проводников и медиана значений плотностей тока, разогревающего проводники до температуры испытаний Т₁, Т₂, Т₃ соответственно.