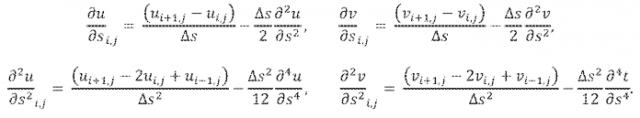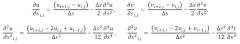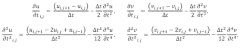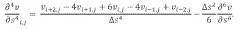Вычисление скважинных диаграмм при искривленных скважинах

Вычисление скважинных диаграмм при искривленных скважинах

Иллюстрации

Показать все

Реферат

Перекрестная ссылка на родственные заявки

[01] По этой заявке испрашивается преимущество приоритета заявки №61/552812 на патент США под названием «Modified Everitt-Jennings with dual iteration on the damping factors and adaptation to deviated wells by including Coulombs friction», поданной 28 октября 2011 г.; заявки №61/598438 под названием «Modified Everitt-Jennings with dual iteration on the damping factors», поданной 14 февраля 2012 г.; заявки №61/605325 под названием «Implementing Coulombs friction for the calculation of downhole cards in deviated wells», поданной 1 марта 2012 года, и заявки № 61/706489 под названием «Iterating on damping when solving the wave equation and computation on fluid load lines and concavity testing», поданной 27 сентября 2012 г., каждая из которых полностью включена в эту заявку путем ссылки. Кроме того, эта заявка подана одновременно с совместно рассматриваемыми заявками (205-0322US1) под названием «Fluid load line calculation and concavity test for downhole pump card», (205-0322US2) под названием «Calculating downhole pump card with iteration on single damping factor» и (205-0322US3) под названием «Calculating downhole pump card with iterations on dual damping factors», каждая из которых включена в эту заявку путем ссылки.

Предпосылки создания раскрытия

А. Штанговая насосная система

[02] Насосные системы с возвратно-поступательным движением, такие как штанговые насосные системы, извлекают флюиды из скважины, и в них используется скважинный насос, соединенный с приводным источником на поверхности. Колонна насосных штанг соединяет наземный приводной источник со скважинным насосом в скважине. При работе источник возбуждения циклически поднимает и опускает штанги скважинного насоса, и при каждом ходе скважинный насос поднимает скважинные флюиды к поверхности.

[03] На фиг.1 показана для примера штанговая насосная система 10, используемая для добычи флюида из скважины. Скважинный насос 14 имеет цилиндр 16 с всасывающим клапаном 24, расположенным внизу. Всасывающий клапан 24 позволяет флюиду входить из буровой скважины, но не позволяет выходить флюиду. Внутри цилиндра 16 насоса плунжер 20 имеет нагнетательный клапан 22, расположенный наверху. Нагнетательный клапан 22 позволяет флюиду перемещаться снизу от плунжера 20 вверх в насосно-компрессорную колонну 18, но не позволяет флюиду возвращаться из насосно-компрессорной колонны 18 в цилиндр 16 насоса ниже плунжера 20. Приводной источник (например, станок-качалка 11) на поверхности соединен колонной 12 насосных штанг с плунжером 20 и перемещает плунжер 20 вверх и вниз циклически при движениях вверх и движениях вниз.

[04] Во время хода вверх нагнетательный клапан 22 закрывается, и любой флюид выше плунжера 20 в насосно-компрессорной колонне 18 поднимается к поверхности. Тем временем всасывающий клапан 24 открывается и позволяет флюиду входить в цилиндр 16 насоса из буровой скважины. Наивысшую точку движения плунжера обычно называют «верхней точкой хода» (TOS), тогда как самую низкую точку движения плунжера обычно называют «нижней точкой хода» (BOS).

[05] В верхней точке хода всасывающий клапан 24 закрывается и удерживает флюид, который вошел в цилиндр 16 насоса. В дополнение к этому в верхней точке хода масса флюида в насосно-компрессорной колонне 18 поддерживается нагнетательным клапаном 22 в плунжере 20 и, следовательно, также и колонной 12 насосных штанг, что вызывает растяжение колонны 12 насосных штанг.

[06] Во время хода вниз нагнетательный клапан 22 сначала остается закрытым до тех пор, пока плунжер 20 не достигает поверхности флюида в цилиндре 16. Ниже нагнетательного клапана 22 создается давление, достаточное для выравнивания давления. При возрастании давления в цилиндре 16 насоса снижается нагрузка на колонну 12 насосных штанг, так что напряжение колонны 12 насосных штанг уменьшается.

[07] Этот процесс происходит в течение ограниченного времени, когда плунжер 20 покоится на флюиде, а станок-качалка 11 на поверхности обеспечивает движение вниз верхней части колонны 12 насосных штанг. Положение плунжера 20 насоса в этот момент времени известно как «точка перехода», поскольку нагрузка столбом флюида в насосно-компрессорной колонне 18 переходит от нагнетательного клапана 22 к всасывающему клапану 24. Это приводит к быстрому снижению нагрузки на колонну 12 насосных штанг во время перехода.

[08] После выравнивания давления нагнетательный клапан 22 открывается, и плунжер 20 продолжает движение вниз до самого нижнего положения (то есть до нижней точки хода). Движение плунжера 20 от точки перехода к нижней точке хода известно как «ход флюида» и является мерой количества флюида, поднимаемого насосом 14 при каждом ходе. Иначе говоря, часть хода плунжера насоса ниже точки перехода можно интерпретировать как процент хода плунжера насоса, при котором удерживается флюид, и этот процент соответствует наполняемости насоса. Поэтому точку перехода можно вычислить при использовании подсчета наполняемости насоса.

[09] Если в буровой скважине находится достаточное количество флюида, цилиндр 16 насоса может полностью заполняться флюидов в продолжение хода вверх. Все же при некоторых условиях насос 14 может не полностью заполняться флюидом при ходе вверх, вследствие чего может оставаться пустое пространство между флюидом и плунжером 20, когда он продолжает подниматься. Работа насосной системы 10 с только частично заполняемым цилиндром 16 является неэффективной и, следовательно, нежелательной. В этом случае о скважине говорят, что она «откачана», а это состояние известно как «удары плунжера о дно цилиндра», при которых могут повреждаться различные компоненты насосной системы. В случае откачанной скважины наиболее вероятно, что точка перехода будет наблюдаться после верхней точки хода плунжера 20.

[10] Обычно датчики для измерения условий возле скважинного насоса 14, который может быть расположен под землей на глубине нескольких тысяч футов, отсутствуют. Вместо них используют численные способы для вычисления положения плунжера 20 насоса и нагрузки, действующей на плунжер 20, на основании измерений положения колонны 12 насосных штанг и нагрузки на нее около станка-качалки 11, расположенного на поверхности. Эти измерения обычно выполняют в верхней части полированного штока 28, который является частью колонны 12 насосных штанг, проходящей через сальниковую коробку 13 в устье скважины. Контроллер 26 насоса используют для мониторинга насосной системы 10 и управления ею.

[11] Для эффективного управления насосной системой 10 с возвратно-поступательным движением и исключения дорогого технического обслуживания контроллер 26 штангового насоса может собирать системные данные и соответственно корректировать рабочие параметры системы 10. Обычно контроллер 26 штангового насоса собирает такие системные данные, как нагрузка и перемещение колонны насосных штанг, путем измерения этих свойств на поверхности. Хотя этими измеряемыми на поверхности данными предоставляется полезная диагностическая информация, они не дают точного представления относительно некоторых свойств, наблюдаемых в скважине возле насоса. Поскольку эти скважинные свойства невозможно без труда измерять непосредственно, их обычно вычисляют на основании измеряемых на поверхности свойств.

[12] В способах определения рабочих характеристик скважинного насоса 20 используют форму графического представления скважинных данных для вычисления различных деталей. Например, в патенте США №5252031 (Gibbs) под названием «Monitoring and pump-off control with downhole pump cards» изложен способ мониторинга снабженной штанговым насосом скважины для обнаружения различных проблем, связанных с насосом, с использованием измерений, выполняемых на поверхности, для образования диаграммы скважинного насоса. В таком случае представленную графически диаграмму скважинного насоса можно использовать для обнаружения различных проблем, связанных с насосом, и управления насосной установкой. Другие способы определения рабочих характеристик раскрыты в публикациях №2011/0091332 и №2011/0091335 заявок на патенты США, которые полностью включены в эту заявку путем ссылки.

В. Способ Эверитта-Дженнингса

[13] В способах определения рабочих характеристик штанговой насосной системы 10, показанной выше, при анализе с помощью программного обеспечения вычисляют скважинные данные (то есть диаграмму насоса) с использованием данных о положении и нагрузке, измеряемых на поверхности. В наиболее точных и популярных из этих способов вычисляют скважинную диаграмму на основании наземных данных путем решения одномерного уравнения затухающей волны, в котором используют положение поверхности и нагрузку, регистрируемые на поверхности.

[14] Существуют различные алгоритмы для решения волнового уравнения. Снайдер решил волновое уравнение, используя способ характеристик. См. Snyder W.E., «A method for computing down-hole forces and displacements in oil wells pumped with sucker rods», Paper 851-37-K, 1963. Гиббс использовал разделение переменных и ряд Фурье, и его способ может быть назван «способом Гиббса». См. Gibbs S.G. et al., «Computer diagnosis of down-hole conditions in sucker rod pumping wells», JPT (Jan. 1966) 91-98; Trans., AIME, 237; Gibbs S.G., «A review of methods for design and analysis of rod pumping installations», SPE 9980, 1982; и патент США № 3343409.

[15] В 1969 г. Кнапп применил конечные разности для решения волнового уравнения. См. Knapp R.M., «A dynamic investigation of sucker-rod-pumping», MS thesis, U. of Kansas, Topeka (Jan. 1969). Этот же способ использовали Эверитт и Дженнингс. См. Everitt T.A. and Jennings J.W., «An improved finite-difference calculation of downhole dynamometer cards for sucker-rod pumps», SPE 18189, 1992; и Pons-Ehimeakhe V., «Modified Everitt-Jennings algorithm with dual iteration on the damping factors», 2012 Southwestern Petroleum Short Course. Кроме того, способ Эверитта-Дженнингса был реализован и модифицирован компанией Weatherford International. См. Ehimeakhe V., «Comparative study of downhole cards using modified Everitt-Jennings method and Gibbs method», Southwestern Petroleum Short Course 2010.

[16] Для решения одномерного волнового уравнения в способе Эверитта-Дженнингса используются конечные разности. Колонну насосных штанг разделяют на М конечно-разностных узлов длиной L_i (фут), плотностью ρ_i (фунт·м/фут³) площадью A_i (дюйм²). Если мы допустим, что u=u(x,t) представляет собой перемещение положения x в момент t времени в штанговой насосной системе, то сконденсированное одномерное волновое уравнение будет выражаться как:

v 2 ∂ 2 u ∂ x 2   =   ∂ 2 u ∂ t 2   +   D ∂ u ∂ t ,     (1)

[17] где скорость акустической волны имеет вид v   =   144 E g ρ и D представляет собой коэффициент затухания.

[18] Первую и вторую производную по времени заменяют разностями вперед первого порядка точности и центральными разностями второго порядка точности. Вторую производную по положению заменяют несколько перегруппированной центральной разностью второго порядка точности.

[19] В способе коэффициент D затухания выбирается автоматически при использовании итерации относительно истинного хода (NS) и коэффициента D затухания. Коэффициент D затухания можно вычислить в соответствии с уравнением:

D   =   ( 550 ) ( 144 g ) 2 π ( H P R   −   H H ) τ 2 ( ∑ ρ i A i L i ) S 2 ,     (2)

[20] где H_PR - мощность полированного штока (в лошадиных силах), S - истинный ход (в дюймах), τ - период одного хода (в секундах), а гидравлическую мощность - H_HYD (в лошадиных силах) получают согласно

H_HYD=(7,36·10^-6)QγF_l,     (3)

где Q - производительность насоса (в баррелях в сутки), γ - удельная плотность флюида и F_l - уровень флюида (в футах). Производительность насоса имеет вид:

Q=(0,1166)(SPM)Sd²,     (4)

где SPM - число качаний насосной установки в ходах в минуту, а d является диаметром плунжера.

[21] Дополнительные подробности относительно получения коэффициента D затухания из уравнения (2) и алгоритма исходной итерации относительно истинного хода и коэффициента затухания приведены в Everitt T.A. and Jennings J.W., «An improved finite-difference calculation of downhole dynamometer cards for sucker-rod pumps», SPE 18189, 1992.

[22] В модифицированном способе Эверитта-Дженнингса также используются конечные разности для решения волнового уравнения. Как и ранее, колонну насосных штанг разбивают на М конечно-разностных элементов, а положение и нагрузку (включая напряжение) вычисляют на каждом шаге вниз по буровой скважине. Затем, как показано на фиг. 2, итерацию выполняют относительно истинного хода и коэффициента затухания, при этом для каждого хода коэффициент затухания выбирается автоматически.

[23] Сначала волновое уравнение решают, чтобы вычислить скважинную диаграмму с использованием наземных измерений, а начальный коэффициент D затухания полагают равным 0,5 (блок 42). Начальный истинный ход S₀ определяют из вычисленной диаграммы, а уровень флюида в скважине вычисляют (блок 44). На этой стадии новый коэффициент D затухания вычисляют из уравнения (2) (блок 46) и т.д., и скважинную диаграмму опять вычисляют с учетом нового коэффициента D затухания (блок 48). На основании пересчитанной скважинной диаграммы определяют новый истинный ход S (блок 50).

[24] Затем на этой стадии проверяют, находится ли вновь определенный истинный S вблизи начального или предшествующего истинного хода в пределах некоторого допуска Є (решение 52). Если не находится, то необходима еще одна итерация, и в процессе 40 возвращаются к вычислению коэффициента D затухания (блок 46). Если вновь определенный истинный ход приближается к ранее определенному истинному ходу («да» при принятии решения 52), то итерацию для определения истинного хода можно прекратить и продолжить процесс 40 для выполнения итерации относительно коэффициента D затухания с использованием сходящегося истинного хода S (блок 54). Затем скважинные данные вычисляют с использованием вновь вычисленного коэффициента D затухания (блок 56) и после этого вычисляют мощность H_Pump насоса в лошадиных силах (блок 58).

[25] На этой стадии выполняют проверку, чтобы выяснить, находится ли мощность H_Pump насоса близко к гидравлической мощности H_hyd в пределах некоторого допуска (решение 60). Если да, то процесс 40 заканчивают, поскольку диаграмма скважинного насоса со сходящимися истинным ходом и коэффициентом D затухания успешно вычислена (блок 62). Если мощность H_Pump насоса и гидравлическая мощность H_hyd не находятся достаточно близко друг к другу («нет» при принятии решения 60), то в ходе процесса 40 корректируют текущий коэффициент D затухания в соответствии с отношением мощности H_Pump насоса к гидравлической мощности H_hyd (блок 64). Процесс 40 вычисления диаграммы насоса с этим скорректированным коэффициентом D затухания повторяют до тех пор, пока для насоса значения мощности H_Pump насоса и гидравлической мощности H_hyd не приблизятся друг к другу в пределах заданного допуска (блоки с 56 по 64).

[26] Преимущество автоматической итерации относительно истинного хода и коэффициента затухания, изложенной выше, заключается в том, что коэффициент D затухания корректируется автоматически без вмешательства человека. Поэтому пользователи, управляющие группами скважин от средних до больших, могут не тратить время на ручную коррекцию коэффициента D затухания, которая может требоваться в других способах.

С. Модель криволинейной скважины

[27] Как отмечалось выше, большая часть способов, применяемых в настоящее время для вычисления скважинных данных, с использованием положения поверхности и нагрузки, регистрируемых динамометрической системой на поверхности, основана на модели вертикального ствола, в которой не учитывается искривление скважины. На фиг. 3А для примера схематично показана вертикальная модель 30 вертикальной скважины 18, имеющей колонну 28 насосных штанг, расположенную в ней. В случае вертикальной модели 30 скважины только релевантные силы трения являются вязкостными по природе. Вязкостное трение F_v является результатом действия сил вязкости, возникающих в кольцевом пространстве во время насосного цикла, которые пропорциональны скорости осевого смещения u.

[28] Однако, когда дело касается искривленной скважины, такой как показанная в искривленной модели 32, изображенной в некоторой степени с преувеличением на фиг. 3В, механическое трение F_m возникает вследствие контакта между насосно-компрессорной колонной 18, колонной 28 насосных штанг и соединительными муфтами 29. Хотя этими силами F_m можно пренебрегать, когда скважина является преимущественно вертикальной, их следует учитывать, когда скважина является искривленной. Если в алгоритме, используемом для вычисления скважинных данных, не учитывать механическое трение F_m в случае искривленной скважины, получающаяся скважинная диаграмма может оказаться искаженной. Этого состояния нельзя избежать изменением обусловленного вязкостью коэффициента D затухания в волновом уравнении.

[29] Поэтому вертикальная модель не очень подходит для вычисления скважинных данных, когда штанговую насосную систему 10 используют в искривленной скважине. Прежде всего, динамические свойства колонны 28 насосных штанг являются иными в искривленных скважинах, чем в вертикальных скважинах. Действительно, предполагается, что в вертикальных скважинах колонна 28 насосных штанг не перемещается в поперечном направлении. Однако в искривленных скважинах механическое трение F_m перестает быть пренебрежимо малым, поскольку имеется протяженный контакт между колонной 28 насосных штанг, соединительными муфтами 29 и насосно-компрессорной колонной 18. Кроме того, поскольку скважина является искривленной, некоторые секции колонны 28 насосных штанг могут изгибаться между двумя соединительными муфтами 29 в средней точке резкого поворота, и это также входит в концепцию кривизны колонны 28 насосных штанг.

[30] В приведенных выше уравнениях, рассмотренных применительно к волновому уравнению, силы трения вязкого характера учитываются только в вертикальной модели. Однако же, как подробно описано выше, силы трения, специфические для искривленных скважин, имеют вязкий и механический характер. Хотя механическим трением F_m обычно пренебрегают, оно имеется, поскольку обращает на себя внимание. Например, для решения проблемы относительно кулоновского трения, которое является результатом механического трения в искривленной скважине, наиболее хорошо известный способ был раскрыт Гиббсом и Лукасевичем. См. Gibbs S.G., «Design and diagnosis of deviated rod-pumped wells», SPE Annual Technical Conference and Exhibition, Oct. 6-9, 1991; и Lukasiewicz S.A., «Dynamic behavior of the sucker rod string in the inclined well», Production Operations Symposium, April 7-9, 1991, оба источника включены в эту заявку путем ссылки.

[31] Для решения проблемы механического трения в искривленных скважинах Гиббс модифицировал волновое уравнение путем добавления к нему члена кулоновского трения. Например, в публикации № 2010/0111716 заявки на патент США (Gibbs et al.) в волновое уравнение включен член C(x), который представляет тяговую силу, действующую на штангу и насосно-компрессорную колонну. В противоположность ему Лукасевич получил уравнения осевого и поперечного перемещения штангового элемента, образующие систему связанных дифференциальных уравнений.

D. Уравнения осевого и поперечного перемещения штангового элемента

[32] Как показал Лукасевич, колонна насосных штанг в искривленной скважине перемещается в продольном направлении вверх и вниз (то есть в осевом направлении) и также перемещается в стороны (то есть в поперечном направлении). Поэтому поведение волн осевого напряжения, а также волн поперечного напряжения в штанговом элементе можно анализировать, чтобы лучше характеризовать поведение колонны 28 насосных штанг в искривленной скважине.

[33] Для этого на фиг. 4 схематически представлено поведение штангового элемента 34 штанговой насосной системы в модели 32 искривленной скважины. На этом схематическом изображении показаны различные силы, действующие на штанговый элемент 34 в осевом и поперечном направлениях. Как представлено здесь, u(s,t) является осевым перемещением штангового элемента 34 длиной ds, а v(s,t) является поперечным перемещением штангового элемента 34. Радиус R_φ кривизны можно вычислять, как и траекторию буровой скважины, в прямоугольных координатах при использовании инклинометрии. Для таких вычислений имеются несколько способов, таких как способ минимальной кривизны или способ радиуса кривизны, раскрытые Гиббсом в Gibbs S. G., «Design and diagnosis of deviated rod-pumped wells», SPE Annual Technical Conference and Exhibition, Oct. 6-9, 1991, источник включен в эту заявку путем ссылки.

[34] На диаграмме сил, действующих на штанговый элемент 34, радиус R_ кривизны показан в виде стрелки, проходящей от центра кривизны к штанговому элементу 34 длиной ds. Осевая сила, обозначенная F, действует на штанговый элемент 34 в направлении вверх и вниз. Поэтому осевая сила имеет осевую составляющую, а также поперечную составляющую. Сила F_t кулоновского трения в точке контакта между штанговым элементом 34 и насосно-компрессорной колонной 18 противоположна движению штангового элемента 34. Масса W показана как гравитационная сила, тянущая вниз штанговый элемент 34. Нормальная сила N действует на штанговый элемент 34 перпендикулярно в направлении к центру кривизны. Масса W и нормальная сила N также имеют осевую и поперечные составляющие.

[35] Таким образом, осевое направление (то есть направление, тангенциальное к штанге) можно характеризовать следующим уравнением движения:

∂ F ∂ s   −   A γ ∂ 2 u ∂ t 2   +   γ g A cos θ   −   D ∂ u ∂ t   −   F t   =   0 .     (1)

[36] В этом уравнении F - осевая сила, действующая на штангу, u(t) - осевое перемещение, А - площадь поперечного сечения штанги, γ - плотность, g - ускорение силы тяжести, θ - угол наклона, D - коэффициент вязкостного затухания, F_t - сила трения со стороны насосно-компрессорной колонны 18, s - длина, измеряемая вдоль криволинейной штанги, и t - время.

[37] Как отмечалось выше, сила F_t представляет собой силу кулоновского трения, являющуюся нелинейной силой, которая направлена противоположно движению материальных тел в механической системе. Кулоновское трение представляет собой сухое трение, которое препятствует относительному поперечному движению двух твердых поверхностей, находящихся в контакте. Относительное движение колонны 28 насосных штанг, насосно-компрессорной колонны 18 и соединительных муфт, прижатых друг к другу, как это видно из фиг. 1, является источником рассеяния энергии, когда скважина откачана.

[38] В поперечном направлении уравнение поперечного движения можно охарактеризовать как:

E I ∂ 2 ∂ s 2 [ ∂ 2 v ∂ s 2   +   1 R ϕ ]   +   γ A ∂ 2 v ∂ t 2   +   n t   +   n p   +   D t ∂ v ∂ t   +   F R   −   γ g A sin θ   =   0 ,   (2)

E I ∂ 4 v ∂ s 4   +   E I ∂ 2 ∂ s 2 1 R ϕ   +   γ A ∂ 2 v ∂ t 2   +   n t   +   n p   +   D t ∂ v ∂ t   +   F R   −   γ g A sin θ   =   0 .

[39] В этих уравнениях EI - изгибная жесткость, Е - модуль упругости Юнга, I - изгибающий момент, D_t - коэффициент вязкостного затухания в поперечном направлении, n_t - поперечная нормальная сила со стороны насосно-компрессорной колонны 18 и n_p - поперечная нормальная сила со стороны жидкости под давлением p, а 1 R является фактическим радиусом кривизны, определяемым в соответствии с 1 R   =   1 R ϕ   +   ∂ 2 v ∂ s 2 .

[40] Как показано Лукасевичем, осевую силу можно ввести в уравнение (1) осевого движения, чтобы получить:

∂ 2 u ∂ s 2   +   ∂ v ∂ s · ∂ 2 v ∂ s 2   −   1 a 2 ∂ 2 u ∂ t 2   −   D A E ∂ u ∂ t   +   γ g E cos θ   −   F t A E   =   0 .     (3)

[41] В этом уравнении a - скорость акустической волны в штанговом элементе 34. Кроме того, в предположении, что штанговый элемент 34 лежит на насосно-компрессорной колонне 18 между соединительными муфтами 29, уравнение (1) осевого движения можно перезаписать в виде:

∂ 2 u ∂ s 2   −   1 a 2 ∂ 2 u ∂ t 2   −   D A E ∂ u ∂ t   +   μ R ∂ u ∂ s   +   γ g E cos θ   −   μ E ( γ g sin θ )   =   0 .   (4)

[42] Дополнительные подробности относительно этих уравнений и осевой силы раскрыты в работе Lukasiewicz S.A., «Dynamic behavior of the sucker rod string in the inclined well», Production Operations Symposium, April 7-9, 1991, которая включена в эту заявку путем ссылки.

[43] Как можно видеть, в уравнении (3) осевого движения используется положение колонны насосных штанг на поверхности для вычисления положения в скважине на каждом конечно-разностном узле вниз по буровой скважине до тех пор, пока узел не будет непосредственно над скважинным насосом. Уравнения (3) и (2) осевого и поперечного движения объединяют для образования системы двух связанных нелинейных дифференциальных уравнений четвертого порядка.

[44] Важно заметить, что кулоновское трение (то есть механическое трение, которое возникает в результате контакта между штангами 28, насосно-компрессорной колонной 18 и соединительными муфтами 29) может быть значительным в искривленной скважине и не может быть имитировано при использовании вязкостного затухания. В частности силы кулоновского трения не пропорциональны скорости штангового элемента, поскольку имеются силы вязкостного трения. В некоторых случаях коэффициент вязкостного затухания можно повышать для исключения излишнего трения, но внутрискважинное трение, обусловленное механической частью, не может быть исключено. Если вязкостное затухание станет слишком большим, эффекты механического трения могут оказаться исключенными, но фактически скважинные данные больше не будут представлять то, что происходит в скважинном насосе.

[45] В уравнении (2) второй член является нелинейным и представляет влияние вертикального отклонения на осевое перемещение. Следует заметить, что уравнения, приведенные выше, являются такими же, как уравнения, представленные Лукасевичем, и что в модели, разработанной Гиббсом, игнорируется поперечное перемещение колонны 28 насосных штанг.

[46] Имеется возможность рассматривать механическое трение в случае, когда дело касается искривленных скважин, к которым растет интерес в отрасли промышленности. Часто пользователи пытаются поправить внутрискважинное трение на скважинной диаграмме путем изменения коэффициента вязкостного затухания или путем добавления члена тягового усилия (как это было сделано Гиббсом). Однако же этим можно значительно исказить скважинные результаты и завуалировать скважинные условия.

[47] Хотя в предшествующем уровне техники (и особенно Лукасевичем) были получены уравнения движения колонны насосных штанг в искривленной скважине, необходимы практические способы выполнения вычислений. Это особенно справедливо в случае, когда вычисления выполняются контроллером насоса или другим обрабатывающим устройством, которое может иметь ограниченные возможности обработки.

Краткое описание чертежей

На чертежах:

[48] фиг. 1 - штанговая насосная система с контроллером для управления насосом системы;

[49] фиг. 2 - иллюстрация итерации относительно истинного хода и коэффициента затухания применительно к модифицированному алгоритму Эверитта-Дженнингса для вычисления диаграммы насоса согласно предшествующему уровню техники;

[50] фиг. 3А - схематическое представление модели вертикальной скважины;

[51] фиг. 3В - схематическое представление модели искривленной скважины;

[52] фиг. 4 - схематическое представление динамических свойств штангового элемента из штанговой насосной системы для искривленной скважины;

[53] фиг. 5 - блок-схема последовательности действий процесса вычисления скважинных данных для штанговой насосной системы в искривленной скважине;

[54] фиг. 6А - иллюстрация контроллера насоса согласно настоящему раскрытию для штанговой насосной системы; и

[55] фиг. 6В - структурная схема контроллера насоса для управления штанговой насосной системой и диагностирования ее согласно настоящему раскрытию.

Подробное описание раскрытия

[56] Согласно настоящему раскрытию модифицированный алгоритм Эверитта-Дженнингса используют для вычисления скважинных данных по наземным данным путем решения одномерного уравнения затухающей волны с помощью конечных разностей. Однако в одномерном уравнении затухающей волны учитывается трение только вязкого характера и игнорируется механическое трение всякого вида. Если скважина является по существу вертикальной, механическое трение является незначительным, а получаемые скважинные данные могут быть точными. Однако в искривленных или горизонтальных скважинах необходимо учитывать механическое трение между штангами, соединительными муфтами и насосно-компрессорной колонной. Согласно этому раскрытию модифицированный способ Эверитта-Дженнингса приспособлен к использованию конечных разностей для включения коэффициентов механического трения в вычисление скважинных данных в случае искривленных или горизонтальных скважин.

[57] Для выполнения этого в идее настоящего раскрытия подход конечных разностей используется для интерпретации системы двух связанных нелинейных дифференциальных уравнений, в которые включены силы, действующие на штанговый элемент в искривленной скважине. Учитываются осевое перемещение и поперечное перемещение штангового элемента, обеспечивающие полную модель для анализа скважинных условий. По существу, в идеях настоящего раскрытия используются уравнения, полученные Лукасевичем, которые были описаны ранее и включены в эту заявку путем ссылки. Уравнения осевого и поперечного движения для штангового элемента были приведены в разделе «Предпосылки создания настоящего раскрытия».

[58] Теперь обратимся к фиг.5, на которой представлена блок-схема последовательности действий при выполнении процесса 100 решения системы связанных дифференциальных уравнений для осевого и поперечного перемещений штангового элемента в искривленной скважине. Для производных, которые входят в ранее приведенные уравнения (2), (3) и (4), разложения в ряд Тейлора используют для образования конечно-разностных аналогов (блок 102). Для первой и второй производных используют соответственно центральную разность первого порядка точности и центральную разность второго порядка точности. Для получения дополнительной детальной информации относительно получения аналога второй производной по перемещению обратитесь к Everitt T.A. и Jennings J.W., «An improved finite-difference calculation of downhole dynamometer cards for sucker-rod pumps», SPE 18189, 1988, источник включен в эту заявку путем ссылки.

[59] В частности, конечно-разностные аналоги представлены ниже (нижним индексом i представлен узел на осевом расстоянии колонны насосных штанг и нижним индексом j представлен временной шаг). В случае пространственной дискретизации конечно-разностные аналоги имеют вид:

[60] В случае дискретизации во времени конечно-разностные аналоги имеют вид:

[61] Аналоги производных по времени являются непосредственными. Однако предпочтительно, чтобы производные по пространству более высокого порядка, чем первого, имели конечно-разностные аналоги, распределенные по нескольким уравнениям для согласования с различными коническими свойствами колонны 28 насосных штанг 28. Распределение конечно-разностных аналогов по нескольким уравнениям прежде всего позволит прослеживать изменение Δs длины криволинейной штанги, так что значения положения, нагрузки и напряжения могут быть вычислены на выбранных интервалах вниз по буровой скважине в противоположность интерполяции между фиксированными точками. Эта возможность дает пользователю дополнительную степень свободы при уточнении дискретизации для оптимизации анализа напряжений.

[62] Для взятия производной ч