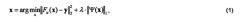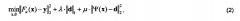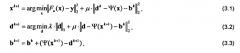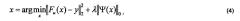Способ и система для быстрой реконструкции изображения мрт из недосемплированных данных

Способ и система для быстрой реконструкции изображения мрт из недосемплированных данных

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение относится к обработке медицинских изображений. В частности, изобретение относится к способу и системе для реконструкции изображения объекта из недосемплированного (частично семплированного) комплексно-значного Фурье-спектра.

Известный уровень техники

Метод визуализации с помощью магнитно-резонансной томографии (МРТ) является неинвазивным и неионизирующим и широко используется в диагностике благодаря его отличной способности визуализировать как анатомическую структуру, так и физиологическую функцию. Однако основной недостаток МРТ состоит в относительно медленном получении изображения, так как используемые данные, измерения (семплы) в так называемом k-пространстве Фурье-спектра объекта получают последовательно во времени. Основополагающий метод восстановления/оценки сигнала по его разреженному/сжатому наблюдению (Compressed sensing, CS), предложенный Donoho (заявка на патент США 2006/0029279), продемонстрировал, что визуализацию по неполным данным можно реконструировать из меньшего количества семплированных данных, т.е. для точной реконструкции изображения в магнитно-резонансной томографии не требуется полное семплирование k-пространства согласно этапам фазового кодирования в импульсной последовательности. Поэтому CS является основным методом для обеспечения аппаратного ускорения МРТ. Для CS-реконструкции можно использовать различные алгоритмы, например полную вариацию (В. Liu et al., ′′Regularized Sensitivity Encoding (SENSE) reconstruction using Bregman iterations,′′ Magnetic Resonance in Medicine 61, 145-152 (2009)) или оптимизацию с регуляризацией l₁ нормы, метод восстановления/оценки сигнала МРТ по его сжатому наблюдению с помощью пересчитываемого (S. Ravishankar and Y. Bresler, ′′Image reconstruction from highly undersampled k-space data by dictionary learning,′′ IEEE Trans, on Med. Imag. 30, 1028-1041 (2011)) или предварительно вычисленного словаря (A. Migukin et al., ′′Phase retrieval in 4f optical system: background compensation and sparse regularization of object with binary amplitude,′′ Appl. Opt. 52, A269-A280 (2013)). Предложенный в настоящем изобретении алгоритм сочетает в себе преимущества высокой производительности и высокой скорости сходимости оптимизации с регуляризацией по l₁-норме, а также эффективности восстановления МРТ-изображения с использованием обученного словаря.

Как отмечалось выше, заявка на патент США 2006/0029279 представляет основу метода восстановления/оценки сигнала по его разреженному/сжатому наблюдению. В ней предложен уже получивший распространение метод, позволяющий точно (с приемлемым качеством) восстанавливать сигналы/изображения, используя значительно меньшее количество измерений, чем количество неизвестных. Основная идея состоит в том, чтобы найти разреженное представление интересующего объекта в избыточных базисах. Однако ввиду слишком общей вариационной постановки задачи оптимизации существует потребность конкретизировать это разрежающее преобразование.

В заявке на патент США 2007/0110290 описан метод реконструкции медицинских изображений из недосемплированных данных, измеренных в k-пространстве, с помощью итеративного алгоритма минимизации. Согласно этому документу реконструкцию выполняют путем безусловной оптимизации сформулированного и/или заранее определенного функционала, который содержит норму разреженного представления пробного изображения, полученного из набора данных, и/или выражение согласованности с данными (невязки). Важным моментом является то, что алгоритм минимизации может содержать подалгоритм метода сопряженных градиентов и/или итерацию Брегмана.

В заявке на патент США 2012/0177128 описана процедура адаптации с целью создания словарей для разреженного представления сигнала/изображения алгоритмом K-SVD. На основании одного или нескольких обучающих сигналов описанная система обработки сигнала формирует словарь, содержащий базисные сигналы-атомы, так что каждый обучающий сигнал можно представить в виде разреженной линейной комбинации сигналов-атомов словаря. Использование избыточных и разреженных представлений продемонстрировано на нескольких эффективных методах, таких как метод поиска соответствий (Matching Pursuit, MP), метод поиска ортогональных соответствий (Orthogonal Matching Pursuit, ОМР), поиска базиса (Basis Pursuit, BP) и алгоритмы Focal Under-determined System Solver (FOCUSS), что соотносится с методом наибольшей апостериорной вероятности (MAP), методом наибольшего правдоподобия (ML), методом независимых компонент (ICA) и методом оптимального направления (MOD).

В заявке на патент США 2012/0259590 описан CS-метод для реконструкции сигнала/изображения из множества векторов измерения, когда сигнал соответствует множеству совместно разреженных векторов. В этом документе предложен способ извлечения информации из множества векторов измерения совместно разреженных сигналов и вычисления подгруппы, имеющей, по меньшей мере, один элемент общего носителя, на основании указанного множества векторов измерения. Разреженное восстановление формулируется посредством вычисления сжатого представления или разреженной аппроксимации к данному вектору путем линейного объединения небольшого числа векторов из группы векторов, известной как словарь.

В качестве недостатков этого и подобных методов можно отметить несколько аспектов. Некоторые из них ориентированы на очень узкую конкретную задачу: известна некоторая предварительная информация о целевом объекте, его свойствах и/или типе использованных данных. Важным моментом каждого CS-алгоритма является его инициализация: почти все авторы публикуют результаты для случая с автоматическим заполнением нулями. Как правило, словари с равновеликими фрагментами изображения (патчами) пересчитываются итеративно.

Сущность изобретения

Настоящее изобретение позволяет решить, по меньшей мере, упомянутые выше проблемы известного уровня и сочетает в себе преимущества высокой производительности и быстрой сходимости, присущие итеративному алгоритму Split Bregman (распределенный алгоритм по Брегману), и эффективность восстановления МРТ-изображения с использованием обученного словаря.

Согласно настоящему изобретению предложен способ для быстрой реконструкции изображения МРТ из недосемплированных данных Фурье-спектра. Основные преимущества включают в себя эффективные процедуры инициализации и разреженной аппроксимации. Согласно изобретению, инициализация алгоритма реконструкции основана на алгоритме Split Bregman или на приближенном разреженном кодировании. Оно существенно повышает точность реконструкции и скорость сходимости. Разреженная регуляризация выполняется посредством предварительно вычисленных словарей с неравновеликими патчами. Это ускоряет вычислительные алгоритмы, потому что не выполняется пересчет словаря, и повышает качество реконструкции благодаря ориентации на недосемплирование используемого Фурье-спектра. Другое преимущество предложенного алгоритма состоит в отдельной обработке Фурье-спектра. Измеренное недосемплированное k-пространство разделяется на две или более полосы частот, которые затем обрабатываются независимо и параллельно. Это позволяет нацеливать словарь на конкретные компоненты различных частот.

Предложенный способ отличается от других высокопроизводительных способов реконструкции изображений МРТ из недосемплированных данных Фурье-спектра следующими аспектами:

- инициализация различного типа (например некоторой константой, разнообразным градиентом или случайной комплексно-значной величиной, объектом, искаженным наложением спектральных компонент, в котором произведена компенсация размытости/подавление шумов/было произведено сглаживание/подчеркивание границ или начальным приближением к объекту, модели объекта или модели сбора данных, первоначальной реконструкцией с использованием итеративного алгоритма Split Bregman, приближенного разреженного кодирования, регуляризированной обратной сверткой, слепой обратной сверткой и т.п.), что обеспечивает существенное подавление эффектов наложения спектральных компонент и значительное повышение скорости сходимости и качества реконструкции;

- использование предварительно вычисленных словарей вместо их итеративного обучения (переобучения) существенно ускоряет вычислительный алгоритм и улучшает реконструированное изображение;

- использование словаря неравновеликих патчей (их наибольший размер ориентирован на недосемплирование) обеспечивает более высокое качество реконструкции;

- разделение спектра реконструированного объекта на две или более полосы частот и их независимая параллельная обработка позволяет более конкретно нацеливать словари на компоненты различных частот.

Краткое описание чертежей

Фиг. 1 иллюстрирует основные этапы способа быстрой реконструкции изображения МРТ.

Фиг. 2 иллюстрирует инициализацию на основе алгоритма Split Bregman.

Фиг. 3 иллюстрирует метод приближенного разреженного кодирования.

Фиг. 4 иллюстрирует метод реконструкции с использованием словаря.

Фиг. 5 иллюстрирует систему, в которой может быть реализован примерный вариант настоящего изобретения.

Подробное описание

Метод визуализации с помощью магнитно-резонансной томографии (МРТ) представляет собой времязатратную процедуру, поэтому важно ускорить получение изображения МРТ. Сигнал МРТ семплируется в спектральном пространстве (так называемом k-пространстве), которое представляет двумерное преобразование Фурье-изображения МРТ. В случае если семплы получают последовательно, то общее время их получения зависит от количества семплов, поэтому одним из способов ускорения получения изображения МРТ является сокращение числа семплируемых частот и реконструкция изображения МРТ только по наблюдаемым частотам (недосемплированному k-пространству).

Предложен способ быстрой реконструкции изображения МРТ из недосемплированного k-пространства. В качестве входных данных способ принимает недосемплированное k-пространство и маску семплирования, которая является бинарной маской, где ′′1′′ означает, что текущая частота семплируется (точка в k-пространстве в соответствующей позиции), а ′′0′′ означает, что текущая частота (точка в k-пространстве в соответствующей позиции) не семплируется. На выходе способ выдает реконструированное изображение.

Согласно настоящему изобретению, способ реконструкции изображения МРТ из недосемплированных данных состоит из нескольких этапов, показанных на фиг. 1. На первом этапе 101 производится съемка спектральных данных с помощью принимающей катушки в k-пространстве в соответствии с заданной схемой семплирования (маской семплирования), в результате чего формируется недосемплированный спектр, подлежащий обработке. Затем выполняется начальная реконструкция 102 путем заполнения несемплированных (пустых) позиций в k-пространстве начальным приближением. На следующем этапе 103 инициализированный спектр (или, иными словами, первоначально реконструированный спектр) в k-пространстве раскладывается на полосы частот, тем самым образуя множество отдельных спектров, соответствующих каждой полосе частот. Затем на этапе 104 каждый полученный спектр реконструируется с помощью алгоритма восстановление/оценки сигнала по его разреженному/сжатому наблюдению с использованием словаря. И наконец, на этапе 105 все реконструированные изображения, соответствующие различным полосам частот, объединяются, используя оператор сложения, и тем самым формируется конечный результат реконструкции, т.е. полный спектр в k-пространстве, соответствующий сигналу МРТ с устраненными размытостью и шумом. В описанной процедуре используется подход на основе обучения для создания словаря, который применяется для реконструкции изображения. Этот словарь обучается предварительно с помощью набора полностью семплированных обучающих МРТ-изображений.

Далее будет представлено более подробное описание упомянутых этапов.

Первоначальная реконструкция

Упрощенный способ восстановления объекта предполагает обратное преобразование Фурье недосемплированных спектральных данных без предварительной обработки. Однако такая реконструкция сильно искажена эффектами наложения спектров из-за наличия нулей в измерениях, особенно в случае равномерного недосемплирования. Простейший способ состоит в заполнении значений в пустых семплах в Фурье-пространстве некоторыми ненулевыми значениями, чтобы избежать наложения спектров и помочь алгоритму реконструкции быстрее достичь сходимости. Эта процедура называется инициализацией или первоначальной реконструкцией. Существует множество подходов к получению первоначальных данных, например: постоянное значение, разнообразный градиент или случайная комплексно-значная величина. Значения в пустых семплах Фурье-спектра можно получить, если объект, искаженный наложением спектральных компонент, предварительно обработать каким-либо методом в пространстве изображения, например путем устранения размытости, шума, путем сглаживания, подчеркивания границ или с помощью какого-либо более сложного метода, например методом регуляризированной обратной свертки, слепой обратной свертки, с помощью итеративного алгоритма Split Bregman или приближенного разреженного кодирования. Это позволяет существенно подавить эффекты наложения спектров и значительно повысить скорость сходимости и качество реконструкции. Также можно использовать некоторую предварительную информацию об объекте, модели объекта или модели сбора данных.

В одном из вариантов изобретения на этапе инициализации 102 можно использовать алгоритм Split Bregman (Т. Goldstein, and S. Osher, ′′The Split Bregman method for L1-regularized problems,′′ SI AM J. on Imag. Sciences 2, 323-343 (2009)). Этот алгоритм обеспечивает эффективность и высокую скорость сходимости в предложенном способе.

Согласно D. L Donoho, ′′Compressed sensing,′′ IEEE Trans. Inf. Theory 52, 1289-1306 (2006), задача CS-реконструкции изначально упрощается и переформулируется как следующая задача поиска базиса шумоподавления (basis pursuit denoising):

что приводит к минимизации выпуклой критериальной функции. Здесь x - вектор изображения объекта, подлежащего реконструкции, F_u преобразование Фурье с частичным семплированием, y - вектор измеренного недосемплированного спектра, Ψ - разрежающее преобразование, λ - параметр регуляризации; l₁ норма | | | | 1 определяется как сумма абсолютных значений элементов вектора, и l₂ норма | | | | 2 определяется как квадратный корень суммы квадратов элементов вектора.

Согласно (Y. Wang et at, ′′A fast algorithm for image deblurring with total variation regularization,′′ CAAM Technical Report (2007)) нормы l₁ и l₂ можно разделить как:

где d - разреженная аппроксимация объекта. Из этого вытекает итеративный алгоритм Split Bregman:

где µ - параметр регуляризации l₁-нормы, а b^k - обновление параметров Брегмана.

На фиг. 2 представлена блок-схема алгоритма инициализации Split Bregman. Согласно Т. Goldstein, and S. Osher, ′′The Split Bregman method for 11-regularized problems,′′ SIAM J, on Imag. Sciences 2, 323-343 (2009), алгоритм содержит два вложенных цикла.

Сначала инициализируются 201 нулевыми векторами вспомогательные переменные разреженной аппроксимации d° объекта и параметр Брегмана b°.

Затем выполняется этап 202, на котором проверяется, завершен ли внешний цикл 202. Если нет, алгоритм переходит к этапу 203, в противном случае алгоритм переходит к этапу 209.

На этапе 203 проверяется, завершен ли внутренний цикл. Если нет, алгоритм переходит к внутреннему циклу, в противном случае алгоритм переходит к этапу 208.

Во время внутреннего цикла выполняются упомянутые выше операции алгоритма Split Bregman (3.1)-(3.3), а именно внутренний цикл включает в себя:

пересчет 204 оценки x^k+1 целевого объекта путем оптимизации l₂-нормы,

пересчет 206 разреженной аппроксимации d^k+1 объекта путем решения l₁-регуляризованной задачи, и

обновление 207 параметров Брегмана b^k+1.

Оптимизация относительно l₁-нормы 206 реализуется посредством операции сравнения с мягким порогом, равным 1/2µ.

Для повышения точности реконструкции и уменьшения числа итераций реконструированный объект можно дополнительно обновить путем восстановления 205 измеренных семплов k-пространства в реконструированном Фурье-спектре объекта x^k+1.

Затем внутренний цикл обновляет вспомогательные независимые переменные 208, которые используются для пересчета 204 оценки объекта.

После выполнения этапа 208 алгоритм возвращается к этапу 202.

Как показано выше, после завершения внешнего цикла 202 алгоритм переходит к этапу 209, на котором полученный объект обновляется снова путем восстановления измеренных семплов k-пространства в реконструированном Фурье-спектре. После этого алгоритм инициализации с использованием алгоритма Split Bregman завершается.

В частности, можно использовать обычный оператор дифференциации в качестве разрежающего преобразования Ψ. В этом случае получаем обычную регуляризацию полной вариации.

Приближенное разреженное кодирование для вычисления начального приближения

В одном из вариантов изобретения начальное приближение можно вычислить методом приближенного разреженного кодирования на этапе инициализации 102. Основная идея метода состоит в использовании обучаемых моделей для прогнозирования разреженных кодов с меньшим числом вычислений, чем в точных алгоритмах. В качестве одного из вариантов обучаемой модели для прогнозирования разреженного кода можно использовать алгоритм обучаемого покоординатного схождения (Learned Coordinate Descent algorithm, LCoD), см., например (Karol Gregor and Yann LeCun, Learning Fast Approximations of Sparse Coding, ICML 2010).

На фиг. 3 показан алгоритм обучения модели для прогнозирования разреженного кода. Для обучения модели следует предварительно определить словарь разреженного кодирования, обучающую последовательность и маску семплирования. Обучающая последовательность должна содержать полностью семплированные данные. На первом этапе 301 обучающего алгоритма из набора данных извлекается полностью семплированное k-пространство. К k-пространству применяется заранее определенная маска семплирования 302, чтобы получить недосемплированное k-пространство, в котором отсутствующие значения заполняются нулями. На этапе 303 путем применения обратного преобразования Фурье реконструируются два изображения: одно из недосемплированного k-пространства (с артефактами в результате заполнения нулями) и другое из полностью семплированного k-пространства. На следующем этапе 304 из обоих изображений извлекаются небольшие фрагменты (патчи) изображения. Размер извлеченного патча равен размеру элемента словаря. Затем выполняется цикл для всех пар патчей (полностью семплированного и недосемплированного). На первом этапе 305 цикла обучаемой моделью прогнозируется разреженный код. Затем реконструируется 306 патч изображения с использованием спрогнозированного кода и заранее определенного словаря. Этот реконструированный патч изображения используется для вычисления 307 погрешности путем сравнения с патчем изображения, извлеченным из полностью семлированного изображения. Используя вычисленную погрешность, параметры модели обновляются 308 любым методом оптимизации, например методом градиентного схождения. Этот процесс повторяется до тех пор, пока процесс обучения достигнет сходимости.

Реконструкция с использованием словаря

Основной частью предложенного способа является этап 104, который основан на разреженной аппроксимации входного сигнала с использованием обученного словаря. На этом этапе решается следующая задача оптимизации:

где l₀-норма | | | | 0 определяется как количество ненулевых компонент вектора.

В методе с использованием словаря разрежающее преобразование представлено разреженным разложением входного сигнала по базисным элементам словаря. Задачу оптимизации, упомянутую выше, решает следующий итеративный алгоритм, показанный на фиг.4. Сначала получают изображение 403 путем применения обратного Фурье-преобразования 402 к входному недосемплированного k-пространства 401. Затем выполняются следующие этапы до достижения сходимости 404 решения. Извлекается 406 набор перекрывающихся патчей 407 из изображения 403. Затем выполняется разреженное разложение 408 для каждого патча. На этом этапе решают следующую задачу оптимизации:

где столбцы X - векторизованные патчи, столбцы z - векторы разреженных кодов, D - матрица преобразования словаря, δ - параметр регуляризации.

В описанной выше задаче элементы словаря 409 представлены в виде столбцов матрицы D, а каждый столбец X должен быть представлен как линейная комбинация элементов словаря с всего небольшим количеством ненулевых компонент (следовательно, столбцы z разреженные).

Данную задачу можно решить с помощью жадного алгоритма поиска ортогонального соответствия (Orthogonal Matching Pursuit). В то время как для каждого патча получают разреженные коды z 410, патчи 412, подлежащие реконструкции, вычисляются как линейная комбинация словарных элементов с вычисленными разреженными кодами как коэффициентами 411. Затем получают промежуточное реконструированное изображение 414 посредством объединения реконструированных перекрывающихся патчей 413. На следующем этапе промежуточное реконструированное изображение 414 преобразуется обратно в частотное пространство путем применения к нему преобразования 415 Фурье, и получается промежуточное k-пространство 416. Затем реконструированные значения в частотах промежуточного k-пространства 416 восстанавливаются (меняются) 417 измеренными данными. Это k-пространство с восстановленными наблюдаемыми частотами 418 преобразуется в пространство изображения посредством обратного преобразования 402 Фурье. Если данное решение сходится 404, то изображение 403 выдается 405 как результат реконструкции, в противном случае начинается новая итерация.

Неравновеликие патчи

Предложенный способ работает с разными методами семплирования. Процедура извлечения патчей из входного изображения формирует набор прямоугольных кусков изображения. Оптимальное соотношение сторон (отношение между шириной и высотой) патча зависит от схемы семплирования k-пространства. Обычный способ семплирования в устройстве МРТ заключается в получении линий фазового кодирования. Эти линии представляют строчки в k-пространстве. Следовательно, информация о частотах теряется вдоль направления у (вертикальная координата). Эти потери вызывают вертикальные искажения из-за наложения спектральных компонент в изображении (полученном из недосемплированного k-пространства). Если число словарных элементов фиксированное, то размер патча не должен быть очень большим в обоих измерениях, потому что будет трудно кодировать такой объем информации лишь небольшим числом элементов. Использование фиксированного объема информации (постоянного числа пикселей) в патче может быть более оптимальным для охвата большего количества данных вдоль вертикального направления при использовании единственного патча. Это применимо, потому что искажения, вызванные наложением спектров, распределены вдоль вертикального направления из-за декартовой схемы семплирования с пропуском линий фазового кодирования. Такая стратегия охвата с фиксированным объемом информации на патч может быть реализована через применение неравновеликих прямоугольных патчей (например при увеличении высоты патча с одновременным уменьшением его ширины). Неквадратные прямоугольные патчи позволяют достичь более высокого качества реконструкции, чем квадратные патчи, при одинаковом или даже меньшем количестве пикселей в прямоугольном патче, чем в квадратном патче. Для недекартовой изотропной схемы семплирования лучше использовать квадратные патчи (качество реконструкции будет выше). В общем случае соотношение сторон патча зависит от отношения потерянной информации вдоль направления х и направления у (величины анизотропии).

Многополосное разложение

В предложенном способе одним из методов использования многоуровневой структуры данных является реконструкция совокупность компонент изображения, соответствующих различным полосам частот, на этапе 103. В этом методе спектр, первоначально реконструированный на этапе 102, разделяется на несколько частей (полос), например соответствующих группе низких, средних и высоких частот, и т.п. При таком разделении появляется несколько новых разбиений k-пространств, каждое из которых содержит только частоты из соответствующей полосы, тогда как другие частоты заполнены нулями и отмечены как измеренные. Разложение сигнала МРТ на полосы частот уменьшает многообразие сигналов в пределах полосы (в каждой полосе сигнал имеет простую форму) и поэтому увеличивает разреженность сигнала и качество конечной реконструкции. Такие усеченные k-пространства обрабатываются как входные данные в основной цикл реконструкции с использованием словаря на этапе 104 и обрабатываются параллельно. После завершения реконструкции изображений для каждой полосы на этапе 105 получают окончательное реконструированное изображение посредством сложения реконструированных изображений для всех полос. На стадии обучения словаря каждое обучающее изображение разлагается на полосы частот одинаковым способом, и индивидуальный словарь обучается отдельно для каждой полосы. На стадии реконструкции каждую полосу реконструируют с использованием соответствующего словаря. Если все частоты в текущей полосе измерены, реконструкцию полосы выполняют просто применением обратного Фурье преобразования. Выбор форм полосы зависит от схемы семплирования. Например для одномерного декартова семплирования полосы представляют собой прямоугольные полоски в k-пространстве, которые ориентированы в том же направлении, что и линии семплирования. Для радиально-симметричного или изотропного произвольного семплирования полосы представляют собой концентрические кольца, центрированные на нулевой частоте.

Система для реконструкции изображения МРТ из недосемплированных данных

На фиг. 5 изображена система, в которой может быть реализован примерный вариант изобретения. Система содержит медицинское оборудование 501 для получения недосемплированных k-пространств, сервер реконструкции 502 и пульт оператора 503. После получения недосемплированного k-пространства с помощью медицинского оборудования файл с этими данными сохраняется в памяти 505 сервера реконструкции. Оператор, используя пульт 507, запускает программу выполнения реконструкции изображения. Программа выполняется на серверном процессоре 504 и содержит модуль 508 для реконструкции недосемплированных данных МРТ как подпрограмму. Результат программы можно выводить на дисплей 506 пульта.

Промышленная применимость

Настоящее изобретение можно использовать в МРТ-сканерах, чтобы ускорить получение изображения, и можно реализовать в программной или аппаратной части медицинского оборудования.

1. Способ реконструкции изображения магнитно-резонансной томографии (МРТ) из недосемплированных данных, содержащий этапы, на которых:получают недосемплированный спектр в k-пространстве с помощью приемной катушки,выполняют первоначальную реконструкцию путем заполнения несемплированных позиций в k-пространстве начальным приближением,выполняют многополосное разложение первоначально реконструированного спектра на ряд отдельных спектров,выполняют реконструкцию с использованием словаря изображений, соответствующих разложенных полосам, иобъединяют реконструированные изображения для получения результирующего целевого изображения,отличающийся тем, что:a. первоначальную реконструкцию выполняют посредством оптимизации критериальной функции, включающей упрощение l₀-нормы;b. многополосное разложение применяют к первоначально реконструированному спектру в k-пространстве для получения ряда отдельных спектров для разных полос частот;c. реконструкцию с использованием словаря выполняют посредством чередования разреженной аппроксимации и восстановления измеренных частот;d. объединение реконструированных изображений дает конечный результат в виде суммы результатов реконструкции каждой полосы частот.

2. Способ по п. 1, в котором регуляризацию l₀ нормы упрощают через оптимизацию l₁-нормы.

3. Способ по п. 2, в котором оптимизацию l₁нормы реализуют посредством способа на основе алгоритма Split Bregman (распределенного алгоритма по Брегману) или способа приближенного разреженного кодирования.

4. Способ по п. 3, в котором способ на основе алгоритма Split Bregman включает в себя восстановление измеренных семплов в k-пространстве в реконструированном спектре во время внутренних итераций Брегмана.

5. Способ по п. 3, в котором способ на основе алгоритма Split Bregman включает в себя восстановление измеренных семплов в k-пространстве в реконструированном спектре после завершения процедуры алгоритма Split Bregman.

6. Способ по п. 3, в котором способ приближенного разреженного кодирования включает в себя:a. сбор набора данных из полностью семплированных k-пространств;b. подготовку недосемплированных данных из полностью семплированных данных путем применения маски семплирования;c. обучение модели прогнозировать разреженные коды для недосемплированных данных, используя полностью семплированные данные для вычисления погрешности;d. прогнозирование приближенных разреженных кодов из недосемплированных данных с использованием обученной модели.

7. Способ по п. 1, в котором упомянутая разреженная аппроксимация включает в себя извлечение неравновеликих перекрывающихся патчей из входного изображения, соответствующего входному сигналу МРТ, выполнение разреженного разложения патчей на разреженные коды с использованием словаря, реконструкцию патчей разреженными кодами и словарем и реконструкцию изображения реконструированными патчами.

8. Способ по п. 7, в котором упомянутый словарь обучают заранее с использованием патчей, извлеченных из набора полностью семплированных обучающих изображений МРТ.

9. Способ по п. 7, в котором словарь обучают отдельно для каждой полосы частот.

10. Способ по п. 7, в котором разреженное разложение выполняют посредством минимизации числа ненулевых компонент в представлении патча как линейной комбинации элементов словаря.

11. Способ по п. 7, в котором упомянутые неравновеликие патчи имеют соотношение сторон, зависимое от величины анизотропии схемы семплирования.

12. Способ по п. 7, в котором упомянутые патчи имеют неквадратную прямоугольную форму для одномерного декартового семплирования и других анизотропных схем и имеют наибольший размер в направлении наибольших информационных потерь в недосемплированном k-пространстве.

13. Способ по п. 7, в котором патчи имеют квадратную форму для изотропной схемы семплирования.

14. Способ по п. 1, в котором реконструкцию с использованием словаря выполняют для каждого k-пространства, соответствующего различной полосе частот.

15. Способ по п. 1, в котором разложенные k-пространства, соответствующие полосам частот, состоят из частот, взятых из первоначально реконструированного k-пространства, соответствующего текущей полосе частот, тогда как другие частоты заполняются нулями и отмечаются как измеренные.

16. Способ по п. 1, в котором дополнительно отображают конечный результат на дисплее.

17. Система для реконструкции изображений магнитно-резонансной томографии (МРТ) из недосемплированных данных, содержащая:медицинское оборудование, выполненное с возможностью:получения недосемплированного спектра в k-пространстве с помощью приемной катушки ипередачи недосемплированного k-пространства в сервер реконструкции;сервер реконструкции, содержащий процессор и память, подключенную к процессору, причем сервер реконструкции выполнен с возможностью:приема и сохранения недосемплированного k-пространства, переданного из медицинского оборудования,выполнения первоначальной реконструкции посредством заполнения начальным приближением несемплированных позиций в k-пространстве,выполнения многополосного разложения первоначально реконструированного спектра на ряд отдельных спектров,выполнения реконструкции с использованием словаря изображений, соответствующих разложенным полосам,объединения реконструированных изображений для получения результирующего целевого изображения, ипередачи результата объединения на пульт оператора; ипульт оператора, содержащий дисплей и контроллер, причем пульт оператора выполнен с возможностью:приема результата объединения от сервера реконструкции, иотображения результата объединения на дисплее;отличающаяся тем, чтоa. первоначальную реконструкцию выполняют посредством оптимизации критериальной функции, включающей упрощение l₀-нормы;b. многополосное разложение применяют к первоначально реконструированному спектру в k-пространстве для получения ряда отдельных спектров для разных полос частот;c. реконструкцию с использованием словаря выполняют посредством чередования разреженной аппроксимации и восстановления измеренных частот;d. объединение реконструированных изображений дает конечный результат в виде суммы результатов реконструкции каждой полосы частот.

18. Система по п. 17, в которой пульт оператора дополнительно выполнен с возможностью: приема ввода от оператора на выполнение реконструкции изображения, формирования команды реконструировать изображение и передачи этой команды в сервер реконструкции; и сервер реконструкции дополнительно выполнен с возможностью приема команды с пульта оператора и выполнения реконструкции изображения.