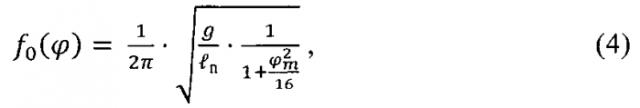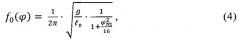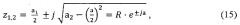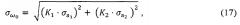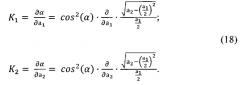Способ калибровки датчика углового ускорения

Способ калибровки датчика углового ускорения

Иллюстрации

Показать все

Реферат

Изобретение относится к области механических измерений, в частности к измерению углового ускорения, применительно к стендам для определения моментов инерции тел.

В настоящее время силами специалистов ЦАГИ разработаны стенды для измерения массы, координат центра масс и моментов инерции изделий машиностроения различного назначения (Богданов В.В., Веселов Н.В., Панченко И.Н. и др. Стенд для измерения массы, координат центра масс и тензора инерции изделия. // Датчики и системы, 2010, №6, с. 24-28), (Богданов В.В., Веселов Н.В., Панченко И.Н. и др. // Патент 2358880 РФ, Стенд для измерения массы, координат центра масс и тензора инерции изделия), (Богданов В.В., Панченко И.Н., Някк В.А., Чумаченко Е.К. // Патент 2434213 РФ, Стенд для измерения массы, координат центра масс и тензора инерции изделия), (Богданов В.В., Панченко И.Н. К теории измерения массы, координат центра масс и моментов инерции тел.// Датчики и системы, 2013, №8, с. 12-15), (Богданов В.В., Панченко И.Н., Чумаченко Е.К. Цифровая обработка сигналов и результаты тестирования стенда. // Датчики и системы, 2010, №5, с. 29-33).

При измерении моментов инерции изделию задают угловые колебания вокруг неподвижных осей стенда. По параметрам, полученным от датчиков момента и датчиков угловых ускорений, вычисляют моменты инерции изделий. На практике из-за компоновки изделия на стенде не удается расположить датчики угловых ускорений на осях, вокруг которых происходит колебания, и их устанавливают на некотором расстоянии L от оси вращения (см. приложение), тогда датчик, кроме углового ускорения, испытывает и линейное ускорение. Для измерения углового ускорения разработан датчик углового ускорения (ДУУ), позволяющий с высокой точностью селектировать сигналы углового ускорения из смеси линейного и углового ускорений, одновременно действующих на датчик.

Применяемые на стендах ДУУ периодически калибруют.

Известен способ воспроизведения и передачи рабочим средствам измерения (в том числе датчикам) размера единицы постоянного углового ускорения (см. Государственный первичный эталон и общесоюзная поверочная схема для средств измерений постоянного углового ускорения в диапазоне , ГОСТ 8.289-78). В качестве образцовых средств измерений применяют образцовые меры, работающие на принципах: падающего в аэростатическом подвесе винта, блока с падающим грузом, управляемых электродвигателей. Образцовые средства измерений применяют для проверки рабочих угловых акселерометров методом прямых измерений. В качестве рабочих средств измерений применяют угловые акселерометры, допускаемые относительные погрешности которых доходят 15%.

Недостаток указанных способов для калибровки ДУУ заключается в следующем. В системе стенда для определения моментов инерции ДУУ измеряют переменное угловое ускорение на некоторой фиксированной частоте колебаний ƒ₀. Калибровка датчика на постоянном угловом ускорении не позволяет учесть динамическую погрешность датчика, возникающую при измерении переменного ускорения. Кроме того, остается открытым вопрос о влиянии линейного ускорения на показания датчика.

Наиболее близким к предлагаемому решению является способ калибровки датчика переменного углового ускорения, используемый при измерении динамических моментов в электроприводах (см. Соколов М.М., Масандилов Л.Б. Измерение динамических моментов в электроприводах переменного тока, стр. 154…156 // Издательство «Энергия», Москва. 1975 г.)

Датчик углового ускорения устанавливают на вал электродвигателя, при этом совмещают ось ДУУ с осью вращения вала электродвигателя и на валу устанавливают штатный датчик угловой скорости ω₀. ДУУ подвергают действию известного углового ускорения и путем обработки выходного сигнала ДУУ находят коэффициент преобразования углового ускорения в электрический сигнал.

Выходной сигнал датчика углового ускорения:

где: k - коэффициент преобразования углового ускорения в электрический сигнал;

- мгновенное значение углового ускорения.

Электропривод разгоняют, на вал действует угловое ускорение и угловая скорость растет.

Для определенного интервала кривой разгона записывают интеграл от левой и правой частей формулы (1):

где: t₁ и t₂- границы интервала кривой углового ускорения;

ω₁ и ω₂ - границы интервала кривой угловой скорости.

Откуда:

где: - площадь под кривой сигнала датчика ускорения на интервале времени с границами t₁ и t₂.

Δω - интервал угловых скоростей с границами ω₁ и ω₂.

Основной недостаток данного способа калибровки ДУУ заключается в том, что он не пригоден для знакопеременных ускорений. Если ускорение изменяется по периодическому закону, что имеет место на стендах, измеряющих моменты инерции, интегралы (2) обращаются в ноль, либо имеют слишком малую величину, непригодную для дальнейшей обработки. Кроме того, указанный способ не позволяет производить калибровку датчика при одновременном действии углового и линейного ускорений.

Задачей данного изобретения является предложение способа калибровки, при котором датчик первоначально подвергают действию только углового ускорения (без действия линейного ускорения), а затем действию такого же углового ускорения и линейного ускорения одновременно.

Техническим результатом предлагаемого способа является повышение точности калибровки ДУУ в условиях, максимально приближенных к условиям его работы на стенде для измерения моментов инерции, определение коэффициента преобразования углового ускорения в выходной сигнал датчика и определение влияния вектора линейного ускорения на этот коэффициент.

Технический результат достигается тем, что в способе калибровки датчика углового ускорения его (датчик углового ускорения) устанавливают на вал, подвергают его действию известного углового ускорения и путем обработки выходного сигнала датчика находят коэффициент преобразования углового ускорения в электрический сигнал, при этом датчик углового ускорения устанавливают на маятнике, его ось совмещают с осью вращения маятника, а ось динамического аналога датчика - с точкой маятника, отстоящей от его оси вращения на заданном расстоянии, маятник отклоняют на допустимый по условию изохронности угол φ_(t=0)≤8° и отпускают, производят дискретные отсчеты сигналов датчика угла α_(n) и углового ускорения , по дискретным отсчетам сигнала датчика угла рассчитывают коэффициенты цифрового режекторного фильтра, которые используют для определения собственной круговой частоты колебаний маятника:

,

где: ω₁ - собственная круговая частота колебаний маятника;

- угол поворота собственного вектора характеристического уравнения;

а₁ и а₂ - коэффициенты цифрового фильтра;

- оптимальное целое число шагов задержки сигнала в цифровом фильтре;

- частота дискретизации сигнала;

- коэффициент затухания колебаний;

по дискретным отсчетам сигналов датчиков угла и углового ускорения рассчитывают коэффициент преобразования углового ускорения в выходной электрический сигнал датчика:

,

где: s - коэффициент преобразования, размерностью ;

- собственная недемпфированная частота колебаний; при этом на величину коэффициента затухания колебаний маятника накладывают ограничение: β≤0,01, после чего датчик углового ускорения и динамический аналог датчика меняют местами и снова определяют коэффициент преобразования датчика в условиях действия на него углового ускорения и вектора линейного ускорения.

Для более подробного пояснения предлагаемого изобретения рассмотрим схему стенда, его конструкцию и принцип действия.

На фиг. 1 показана аксонометрическая проекция стенда для калибровки ДУУ;

На фиг. 2 показаны векторы ускорений, действующие на маятник;

На фиг. 3 приведена структурная схема режекторного (нерекурсивного) цифрового фильтра.

Стенд (см. фиг. 1) состоит из станины 1, на которой закреплен узел поворота 2, на его валу с одной стороны установлен датчик угла 3, а на другой - стержень 4, к которому закреплен груз 5. Стержень и груз образуют маятник. На стержне 4 устанавливают ДУУ 6 и динамический аналог датчика (ДАД) 7, имеющий такие же, как у ДУУ, массу, момент инерции и угловую жесткость. Если на оси вращения устанавливают ДУУ 6, то на расстоянии L от оси вращения закрепляют ДАД 7, причем ось ДУУ 6 совмещают с осью вращения маятника, а ось ДАД 7 - с точкой маятника, отстоящей от оси вращения на заданное расстояние. При установке ДУУ 6 на расстоянии L, на оси вращения устанавливают ДАД 7. Перемещением груза 5 по стержню 4 подбирают необходимую частоту колебаний маятника. ДУУ 6 подвергают действию известного углового ускорения путем колебательных движений маятника. Маятник отклоняют на допустимый по условию изохронности угол φ_(t=0)≅8° (см. фиг. 2) от положения равновесия и отпускают.

Производят дискретные отсчеты сигналов датчика угла α_(n) и углового ускорения , по дискретным отсчетам сигнала датчика угла рассчитывают коэффициенты цифрового режекторного фильтра, которые используют для определения собственной круговой частоты колебаний маятника:

,

где: ω₁ - собственная круговая частота колебаний маятника;

- угол поворота собственного вектора характеристического уравнения;

а₁ и а₂ - коэффициенты цифрового фильтра;

- оптимальное целое число шагов задержки сигнала в цифровом фильтре;

- частота дискретизации сигнала;

- коэффициент затухания колебаний;

по дискретным отсчетам сигналов датчиков угла и углового ускорения рассчитывают коэффициент преобразования углового ускорения в выходной электрический сигнал датчика:

,

где: s - коэффициент преобразования, размерностью ;

- собственная недемпфированная частота колебаний; при этом на величину коэффициента затухания колебаний маятника накладывают ограничение: β≤0,01, после чего датчик углового ускорения и динамический аналог датчика меняют местами и снова определяют коэффициент преобразования датчика в условиях действия на него углового ускорения и вектора линейного ускорения.

Дифференциальное уравнение свободных колебаний маятника вокруг оси вращения (ОВ), параллельной оси Ζ (фиг. 2).

где: Jz - момент инерции маятника относительно оси Z;

l - расстояние между центром масс (ЦМ) маятника и ОВ;

g - ускорение свободного падения;

φ - угол поворота маятника.

Уравнение (3) позволяет найти собственную частоту колебаний маятника, которая в силу нелинейности уравнения зависит от амплитуды угла поворота.

Для малых углов поворота собственная частота маятника определяется зависимостью (см. Маркеев А.П. Теоретическая механика. // М. «Наука», 1990, стр. 155):

где: - приведенная длина маятника: ;

φ_m = максимальный угол поворота маятника.

Поскольку маятник совершает затухающие колебания, то в соответствии с уравнением (4) по мере уменьшения угла поворота частота маятника будет меняться (расти), по этой причине колебания маятника становятся неизохронными.

В результате возникает ошибка в определении частоты, обусловленная неизохронностью колебаний.

Так, для максимального угла отклонения φ_m=8° ошибка составляет 0,12%, а для φ=6° соответственно 0,068%.

Дифференциальное уравнение колебаний маятника с учетом малости угла отклонения и сопротивлении потерь, пропорционального скорости:

где: h - коэффициент сопротивления.

Уравнение (5) путем несложных преобразований приводится к виду:

где: ω₀ - собственная недемпфированная круговая частота маятника:

:

β - коэффициент затухания колебаний:

Если задать маятнику малое начальное отклонение φ_m, из уравнения (6) получим следующий закон изменения угла поворота по времени:

где: ω₁ - собственная демпфированная круговая частота колебаний: ;

Ψ - фазовый угол: .

Закон изменения по времени углового ускорения:

Как видно из уравнения (8), для воспроизведения углового ускорения необходимо знание амплитуды φ_m, собственной круговой частоты ω₀ и коэффициента затухания колебаний β.

Центральной задачей является определение собственной частоты колебаний по дискретным отсчетам сигнала датчика угла α_(n).

Для ее решения цифровую последовательность угла поворота φ(n) пропускают через режекторный (нерекурсивный) цифровой фильтр (фиг. 3) с передаточной функцией:

где: z - оператор дискретного преобразования Лапласа;

m - коэффициент задержки сигнала в цифровом фильтре - целое число больше единицы (вводится с целью повышения точности измерения частоты колебаний);

К - масштабирующий коэффициент:

.

Ζ - преобразование дискретной цифровой последовательности сигнала угла поворота:

После перехода в уравнении (7) к дискретному времени t=m·(n·Δt) и выполнения необходимых преобразований получают:

где: Δt- временной шаг дискретизации сигнала;

R - модуль корней характеристического уравнения, определяется коэффициентами b₁,b_n.

Выражение (11) является общим для класса сигналов, описываемых уравнением (7).

Для определения неизвестных коэффициентов b₁ и b₂ коэффициенты фильтра a₁ и a₂ настраивают таким образом, чтобы выполнялись условия:

при реализации которых фильтр «запирается», в результате чего выходная последовательность фильтра y(n) обращается в ноль.

Подбор коэффициентов a₁ и a₂ осуществляется следующим образом.

В соответствии с передаточной функцией (9) выходная цифровая последовательность фильтра:

Дисперсия y(n) (см. Марпл М.Л. и Марпл С.Л. Цифровой спектральный анализ и его приложения. // Пер. с англ. М., Мир, 1990):

где: N - общее количество отсчетов сигнала.

Для определения коэффициентов имеем два условия:

,

которые приводят к системе N-2m линейных уравнений, решаемых методом наименьших квадратов.

В результате получают (см. Худсон К. Статистика для физиков. // М., Мир, 1970, стр. 152):

где: а - вектор-столбец искомых коэффициентов:

;

φ, s - одностолбцовая и двухстолбцовая матрицы:

Τ - оператор транспонирования матриц.

Корни характеристического уравнения фильтра:

где:

Частота запирания фильтра равна частоте колебаний маятника:

Входящий в выражение (16) угол α определяют коэффициентами a₁ и а₂ цифрового фильтра.

Поскольку коэффициенты содержат погрешности измерений, частота ω₁ также будет измеряться с погрешностью.

Среднеквадратическая погрешность измерения частоты:

где: и - среднеквадратические погрешности коэффициентов а₁ и а₂.

Выполняя дифференцирование уравнений (18), после несложных преобразований получают:

При - погрешность достигает минимума:

и

Подставляя в (16) оптимальное значение , получим:

где: ƒ_д - частота дискретизации сигнала: ;

ƒ₁ - частота колебаний маятника: .

Коэффициент затухания β

В ряде случаев необходимо знать коэффициент затухания β. Такая необходимость возникает при измерении амплитуды угла поворота.

Из уравнения (15):

подставляют в уравнение (22):

,

и производя логарифмирование, после несложных преобразований получают:

Коэффициент преобразования датчика углового ускорения

Источником выходного сигнала ДУУ является тензометрический мост. Выходной сигнал моста, как принято, нормируют в относительных единицах.

В нашем случае: ,

где: - относительный выходной сигнал датчика;

ΔU - сигнальное напряжение;

U_n - напряжение питания моста.

Между сигнальным напряжением и угловым ускорением существует линейная зависимость, которая подтверждается статической калибровкой датчика: ,

где: s - коэффициент преобразования датчика.

Для определения коэффициента преобразования необходимо располагать опорным сигналом, который по форме совпадал бы с сигналом углового ускорения (8) (см. Хелстром К. Статистическая теория обнаружения сигналов. // М., Издательство иностранной литературы, 1963 г.) В качестве опорного берут сигнал угла поворота в уравнении (7).

Дисперсия разности сигналов с учетом дискретного времени:

.

Полагая , находят:

По поводу выражения (24) необходимо сделать следующие замечания.

Дело в том, что сигналы угла поворота и ускорения отличаются по фазе. В первом случае фазовый угол +Ψ, а во втором -Ψ. При стремлении β→0 фазовый угол в соответствии с уравнением (7) стремится к , и сигналы с точностью до знака совпадают по форме.

Обозначают погрешность измерения коэффициента s, обусловленную несовпадением формы сигналов, через и подсчитывают зависимость δ% от коэффициента затухания β.

Результаты расчетов приведены в таблице №1.

Из таблицы №1 находим, что при:

погрешностью от несовпадения формы сигналов можно пренебречь.

Одновременно условие (25) обеспечивает с точностью 0,005% равенство частот ω₀ и ω₁, и, как следствие, частота ω0 перестает зависеть от коэффициента затухания β, который, в свою очередь, зависит от окружающей температуры, давления и других факторов.

Амплитуда угла поворота

Дискретный сигнал угла поворота:

С учетом малости коэффициента затухания колебаний β можно записать:

где:

Дисперсия разности сигналов:

.

Полагая: , находим:

Воспроизведение маятником линейного ускорения

При установке ДУУ на расстоянии l_c от оси вращения маятника на ДУУ кроме углового ускорения действует и линейное ускорение. Чувствительность датчика к линейному ускорению объясняется некоторой остаточной несбалансированностью инерционной массы, выполненной в виде обода, насаженного на осесимметричный тензометрический элемент. Маятник позволяет выполнить, в случае необходимости, добалансировку ДУУ и тем самым свести к допустимому минимуму его чувствительность к линейному ускорению.

С этой целью ось ДУУ первоначально совмещают с осью маятника, где действует только угловое ускорение и отсутствует линейное ускорение.

После чего ДУУ и ДАД меняют местами, т.е. ось ДУУ будет находиться на расстоянии l_c, от оси вращения маятника.

В общем случае вектор линейного ускорения в точке, смещенной на расстояние l_c от оси вращения:

где: u - вектор скорости точки;

τ и ν - единичные взаимно перпендикулярные векторы.

Первый член уравнения (27) представляет центростремительное ускорение. При колебаниях датчика с круговой частотой ω₀, центростремительное ускорение имеет частоту 2ω₀ и при обработке сигнала датчика не учитывается.

Второй член является тангенциальным ускорением с амплитудой:

Маятник наиболее полно моделирует работу ДУУ в системе стенда при измерении моментов инерции, при этом точность калибровки повышается, если частота и амплитуда колебаний, при которых она проводится, близка или совпадает с ожидаемой частотой колебаний соответствующих рам стенда при измерении моментов инерции изделия.

На существующих стендах максимальное удаление датчика углового ускорения от оси вращения изделия составляет величину l≅0,5 м.

При φ_m=8°; ƒ₀=0,8 Гц, a_τ=1,76 м/сек² или a_τ=0,18·g.

Зная показания датчика при действии только углового ускорения и показания датчика при действии дополнительно линейного ускорения, при проведении измерений на стенде вводят поправки, позволяющие получить действующие значения углового ускорения с высокой точностью.

Способ калибровки датчика углового ускорения, заключающийся в том, что датчик углового ускорения устанавливают на вал, подвергают его действию известного углового ускорения и путем обработки выходного сигнала датчика находят коэффициент преобразования углового ускорения в электрический сигнал, отличающийся тем, что датчик углового ускорения устанавливают на маятнике, его ось совмещают с осью вращения маятника, а ось динамического аналога датчика - с точкой маятника, отстоящей от его оси вращения на заданное расстояние, маятник отклоняют на допустимый по условию изохронности угол φ_(t=0)≤8° и отпускают, производят дискретные отсчеты сигналов датчика угла α_(n) и углового ускорения , по дискретным отсчетам сигнала датчика угла рассчитывают коэффициенты цифрового режекторного фильтра, которые используют для определения собственной круговой частоты колебаний маятника: ,где: ω₁ - собственная круговая частота колебаний маятника; - угол поворота собственного вектора характеристического уравнения;а₁ и а₂ - коэффициенты цифрового фильтра; - оптимальное целое число шагов задержки сигнала в цифровом фильтре; - частота дискретизации сигнала; - коэффициент затухания колебаний;по дискретным отсчетам сигналов датчиков угла и углового ускорения рассчитывают коэффициент преобразования углового ускорения в выходной электрический сигнал датчика: ,где: s - коэффициент преобразования, размерностью ; - собственная недемпфированная частота колебаний;при этом на величину коэффициента затухания колебаний маятника накладывают ограничение: β≤0,01, после чего датчик углового ускорения и динамический аналог датчика меняют местами и снова определяют коэффициент преобразования датчика в условиях действия на него углового ускорения и вектора линейного ускорения.