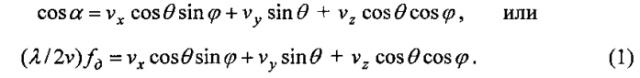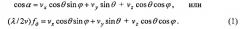Способ формирования трехмерного изображения земной поверхности в бортовой доплеровской рлс с линейной антенной решеткой

Способ формирования трехмерного изображения земной поверхности в бортовой доплеровской рлс с линейной антенной решеткой

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, а именно к бортовым радиолокационным системам наблюдения за земной поверхностью на базе доплеровской радиолокационной станции (РЛС) с линейной антенной решеткой (АР).

Трехмерное изображение участка земной поверхности формируется в виде совокупности пространственных координат элементов отражения земной поверхности в зоне видимости РЛС, определяемой диаграммой направленности (ДН), при фиксированном положении линии визирования антенны. Наличие такого изображения позволяет повысить безопасность маловысотных полетов над сложным рельефом местности.

Известен способ формирования трехмерного изображения поверхности с высотными объектами по данным бортовой импульсно-доплеровской РЛС [1], способ измерения высоты и формирования трехмерного изображения поверхности по данным бортовой импульсно-доплеровской РЛС маловысотного полета [2], а также способ измерения координат элементов земной поверхности в бортовой четырехканальной доплеровской РЛС [3], в которых совместно с селекцией траекторного сигнала по доплеровской частоте применяется моноимпульсный метод измерения угловых координат.

Известны способы измерения угловых координат нескольких объектов в многоканальных доплеровских РЛС [4] и повышения разрешающей способности РЛС по углу при переднебоковом обзоре [5], в которых совместно с селекцией по доплеровской частоте применяется метод решения системы уравнений, или восстановления комплексных амплитуд в точках возможного отражения с искомыми координатами.

Однако все эти способы применимы только для узкой ДН, так как при больших углах отклонения от центрального направления появляется неоднозначность измерения фазы. Устранение неоднозначности требует конструктивных изменений антенны [6, с. 424] и дополнительной алгоритмической обработки. Также при расчете фазовых соотношений следует учитывать поправку на сферичность фронта волны.

В качестве прототипа рассматривается способ [4], который применительно к измерению координат элементов земной поверхности заключается в следующем.

1. Используется АР, Q приемных элементов которой расположены на плоскости антенны в матричном порядке.

2. При данном положении линии визирования антенны, соответствующем переднебоковому обзору бортовой РЛС, получают комплексные траекторные сигналы S ˙ q ( t ) на заданном промежутке времени t синтезирования одновременно в q-x измерительных каналах (номер канала совпадает с номером q приемного элемента антенны: q = 1, Q ¯ , где Q - общее число каналов). Затем эти сигналы селектируют в i-x элементах разрешения дальности R_i. В результате из S ˙ q ( t ) выделяют i-e составляющие S ˙ q ( i , t ) , i=1, 2, …, m, по числу элементов дальности m.

3. В каждом i-м элементе дальности со значением R_i сигналы S ˙ q ( i , t ) преобразуют во временные последовательности S ˙ q ( i , t j ) , j = 1, N ¯ (N - число временных отсчетов на промежутке синтезирования), которые подвергают дискретному преобразованию Фурье (ДПФ). Тем самым селектируют сигнал по доплеровской частоте f_j в каждом q-м канале. В результате из S ˙ q ( i , t ) выделяют j-е составляющие S ˙ q ( i , f j ) , j=1, 2 …, N, в q-x каналах, q = 1, Q ¯ , где N становится числом элементов разрешения по частоте. Данные операции выполняют одновременно (параллельно) в Q каналах.

4. Из N элементов разрешения по частоте рассматривают только те n элементов (n<<N), на которых амплитуда сигнала A q ( i , j ) = | S ˙ q ( i , f j ) | превышает порог обнаружения во всех q-x каналах. Такие элементы разрешения соответствуют элементам отражения земной поверхности.

5. Для каждой i,j-й совокупности измерений S ˙ q = S ˙ q ( i , f j ) , q = 1, Q ¯ находят оценки угловых координат φ - азимута и θ - угла места методом восстановления амплитуд в точках возможного отражения следующим образом.

5.1. Заранее методом восстановления вычисляют комплексные весовые коэффициенты w ˙ q k ( j ) , q = 1, Q ¯ для ряда k-х точек, координаты которых соответствуют доплеровской частоте f_j, j = 1, n ¯ , а их общее число K определено шагом дискретизации.

5.2. Восстанавливают комплексные амплитуды k-х точек по формуле:

5.3. Точка с максимальной амплитудой | U ˙ k ( i , j ) | , превышающей порог обнаружения, принимается за центр элемента отражения поверхности;

5.4. Угловые координаты выбранной точки дают искомые оценки угловых координат φ_ij и θ_ij отражающего элемента поверхности в i-м элементе дальности со значением R_i на j-й доплеровской частоте.

6. Прямоугольные координаты центров i,j-x элементов отражения земной поверхности для узкой ДН вычисляют по формулам:

x_ij=φ_ijR_i, y_ij=θ_ijR_i, z_i=R_i.

7. Совокупность координат x_ij, y_ij, z_ij, полученных на множестве значений i, j, дает трехмерное изображение земной поверхности по ширине ДН, которое отображается на экране индикатора пилота летательного аппарата.

Однако данный способ обладает следующими недостатками.

1. Число каналов обработки Q должно превышать число K предполагаемых точек отражения, что требует повышенных вычислительных затрат.

2. Процедуры восстановления не всегда бывают корректными, и для повышения их устойчивости прибегают к методам регуляризации.

3. Восстановление комплексных амплитуд основано на информации как амплитудных, так и фазовых различий при приеме отраженных сигналов в пространственно разнесенных элементах АР. Однако для больших угловых отклонений относительно центрального направления появляется неоднозначность измерения фазы, что приводит к ошибкам измерения координат. Поэтому область применимости способа ограничена узкой ДН порядка 1°-10°. Для расширения зоны видимости РЛС требуется сканирование лучом антенны вдоль зоны наблюдения.

Технический результат направлен на формирование трехмерного изображения поверхности на базе бортовой РЛС при меньшем числе каналов обработки и для более широкой ДН антенны по сравнению с прототипом за счет использования амплитудного метода измерения координат [6, с. 416], слабо зависящего от фазовых неоднозначностей.

Технический результат предлагаемого технического решения достигается тем, что способ формирования трехмерного изображения земной поверхности в бортовой доплеровской РЛС с линейной антенной решеткой заключается в формировании на заданном промежутке времени синтезирования радиолокационного изображения участка земной поверхности в виде совокупности комплексных амплитуд S ˙ q ( i , j ) сигналов отражения в i-x элементах разрешения дальности R_i (i=1, 2, …, m, где m - число элементов дальности) на j-x частотах (j=1, 2, …, N, где N - число элементов разрешения по частоте) одновременно в Q измерительных каналах ( q = 1, Q ¯ , где q - номер канала), определении тех j-x частот, на которых амплитуда A q ( i , j ) = | S ˙ q ( i , j ) | сигнала S ˙ q ( i , j ) превышает порог обнаружения во всех каналах, и последующей обработке полученных измерений S ˙ q ( i , j ) , q = 1, Q ¯ , отличающийся тем, что при переднебоковом обзоре вектор скорости движения носителя РЛС устанавливают в горизонтальное положение, при котором элемент разрешения по доплеровской частоте однозначно определяет оценку x_ij координаты х в горизонтальной плоскости для i,j-го элемента отражения земной поверхности, а для определения оценки y_ij координаты y в вертикальной плоскости приемные элементы линейной АР располагают вдоль оси y и ориентируют их так, чтобы биссектрисы ДН q-x приемных элементов АР были смещены по углу места θ последовательно на величину шага h_θ=Δ_θ/(Q-1), где Δ_θ - ширина ДН на уровне 0,5 мощности, при этом для каждой совокупности полученных комплексных измерений S ˙ q ( i , j ) , q = 1, Q ¯ , определяют модули A q = | S ˙ q ( i , j ) | и получают распределение амплитуд A_q, q = 1, Q ¯ , с шагом h_θ, затем в последовательности амплитуд выбирают максимальную по q амплитуду, и соответствующий ей номер q дает начальную оценку угла места θ=-Δ_θ/2+(q-1)h_θ, которая уточняется по трем значениям амплитуд A_q-1, A_q, A_q+1 методом параболической интерполяции в сторону точки максимума и дает оценку y_ij=R_i sinθ, указанные операции повторяют на множестве значений i, j и получают совокупность пространственных координат x_ij, y_ij, z_ij, z i j = R i 2 − x i j 2 − y i j 2 , представляющих трехмерное изображение участка земной поверхности.

Способ осуществляют следующим образом.

1. Центры q-x приемных элементов антенны общим числом Q = ( q = 1, Q ¯ ) располагают вдоль линейной АР на оси у в точках с координатами x_q=0, yq=±id, i = 1, n y ¯ , Q=2n_y+1, где 2d - базовое расстояние между центрами приемных элементов. Биссектрисы ДН q-x приемных элементов АР смещены по углу места θ на величину θ_0q таким образом, что амплитудная характеристика ДН каждого q-го канала зависит от θ_0q:

где φ - азимут; k₀ - известный коэффициент; Δ_φ и Δ_θ - ширина ДН по азимуту и углу места на уровне 0,5 мощности.

Практически это достигается за счет пространственной ориентации q-го элемента АР по углу места в направлении θ_0q или электронного управления лучом. Величины θ_0q задаются на промежутке [-Δ_θ/2, Δ_θ/2] с шагом h_θ=Δ_θ/(Q-1).

2. Вектор скорости v → устанавливают в горизонтальной плоскости. В антенной правой системе координат (ось z дает линию визирования антенны, оси x и y расположены соответственно в горизонтальной и вертикальной плоскостях) орт вектора скорости v → 0 = ( v x ,0, v z ) при скорости v, длине волны λ и наклонной дальности R_i определяет координату х элемента отражения на доплеровской частоте f_j:

Направление линии визирования антенны по отношению к вектору скорости соответствует переднебоковому обзору бортовой РЛС.

3. В результате первичной обработки отраженных сигналов получают комплексные траекторные сигналы S ˙ q ( t ) на заданном промежутке времени t синтезирования одновременно в Q каналах, каждый q-й канал обрабатывает сигналы, принятые в q-м приемном элементе линейной АР ( q = 1, Q ¯ ) .

4. Сигналы S ˙ q ( t ) селектируют в i-x элементах разрешения дальности R_i по задержке времени прихода отраженного сигнала. В результате из S ˙ q ( t ) выделяют i-e составляющие S ˙ q ( i , t ) , i=1, 2, …, m, по числу элементов дальности m.

5. В каждом i-м элементе дальности со значением R_i сигналы S ˙ q ( i , t ) преобразуют во временные последовательности S ˙ q ( i , t j ) , j = 1, N ¯ (N - число временных отсчетов на промежутке синтезирования), которые подвергают ДПФ. Тем самым селектируют сигнал по доплеровской частоте f_j в каждом q-м канале. В результате из S ˙ q ( i , t ) выделяют j-е составляющие S ˙ q ( i , f j ) , j=1, 2 …, N, в q-x каналах, q = 1, Q ¯ , где N становится числом элементов разрешения по частоте. Данные операции выполняют одновременно (параллельно) в Q каналах.

6. Из N элементов разрешения по частоте рассматривают только те n элементов (n<<N), на которых амплитуда сигнала A q = | S ˙ q ( i , f j ) | превышает порог обнаружения во всех q-x каналах. Такие элементы разрешения соответствуют элементам отражения земной поверхности. Полученную для данных значений i, j последовательность амплитуд A_q, q = 1, Q ¯ , запоминают как распределение амплитуд A_q, q = 1, Q ¯ , с шагом h_θ.

7. Для i,j-го распределения амплитуд A_q, q = 1, Q ¯ , находят оценку угла места θ и соответствующую ему оценку координаты у следующим образом.

7.1. В последовательности {A_q} выбирают максимальную по q амплитуду A_max=maxA_q. Соответствующий A_max номер q дает начальную оценку угла места: θ₀=-Δ_θ/2+h_θ(q-1).

7.2. Оценку θ₀ уточняют по трем значениям амплитуд A_q-1, A_q, A_q+1, а именно методом параболической интерполяции находят смещение Δθ в сторону точки максимума и вычисляют уточненную оценку θij=θ₀+Δθ.

7.3. Вычисляют оценки координат у и z по формулам:

8. Совокупность координат x_ij, y_ij, z_ij на множестве i, j представляет трехмерное изображение поверхности.

Расчетная часть

В антенной системе связь угловых φ, θ и соответственно прямоугольных x, y координат с доплеровской частотой f_д получается следующим образом. Для режима доплеровского обужения луча (ДОЛ) имеем [7, с. 22, с. 52]: f_д=(2v/λ)cosα, где cosα находится с помощью скалярного произведения двух векторов: v → 0 = ( v x ,   v y ,   v z ) - орта вектора скорости v → движения носителя РЛС и r → 0 = ( cos θ sin ϕ ,   sin θ ,   cos θ cos ϕ ) - орта радиус-вектора r → = ( x , y , z ) точки отражения:

Уравнение (1) при фиксированных v и f_д представляет собой нелинейное уравнение линии доплеровской частоты (изодопы) на дальности R в угловых координатах φ, θ.

Прямоугольные координаты x, y, z точки M(x, y, z) связаны со сферическими координатами R, φ, θ известными зависимостями:

Из (1), (2) получаем линейное уравнение поверхности доплеровской частоты f_i в координатах x, y, z:

v x x + v y y + v z z = c j , c j = R ( λ / 2 v ) f j .         ( 3 )

В частном случае переднебокового обзора, когда вектор скорости носителя РЛС расположен в плоскости xoz: v → 0 = ( v x ,   0,   v z ) и его составляющая v_y=0, уравнение (3) упрощается:

В этом случае (4) представляет собой уравнение вертикальной прямой. При этом координата x однозначно определяется доплеровской частотой f_j: x=c_j/v_x, а координата у подлежит оцениванию.

Результаты моделирования

Способ-прототип с числом каналов Q=25 и предлагаемый способ с числом каналов Q=9 сравнивались методом математического моделирования. Оценивались координаты центров нескольких элементов отражения поверхности на дальности R=1000 м. Точность оценок характеризовалась средней ошибкой определения пространственных координат и СКО этих ошибок при отношении сигнал-шум С/Ш=30 дБ.

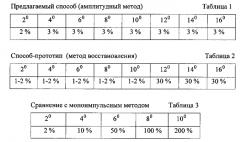
В таблицах 1 и 2 даны зависимости нормированного и усредненного показателя точности, представленного в процентах, от ширины ДН по углу места Δ_θ=2°, 4°, 6°, … при фиксированной ширине по азимуту Δ_φ=2°. Показатель в метрах, усредняющий среднюю ошибку и СКО ошибки, делился на линейную ширину ДН в метрах, которая на дальности R составляла 34, 68, 102, … м.

Виден стабильный характер ошибки предлагаемого способа, в то время как способ-прототип, будучи примерно в 2 раза точнее при Δ_θ=2°-10°, ведет себя по точности в 10 раз хуже предлагаемого способа, начиная с 12°.

Для сравнения в таблицах 3, 4 даны зависимости, полученные в аналогичных условиях моделирования для способа [2] измерения пространственных координат, основанного на моноимпульсном методе (плоская АР с числом каналов Q=4), и способа [6, с. 424], основанного на фазовом методе без дополнительных операций устранения неоднозначности при измерении фазы (плоская АР с числом каналов Q=4). Видно, что работоспособность первого способа ограничена шириной ДН 2° и второго способа - 4°.

Литература

1. Патент RU 2334250 C1.

2. Патент RU 2351949 C1.

3. Положительное решение по заявке №2013119344/07(028620).

4. Патент RU 2373551 C1.

5. Патент RU 2416809 C1.

6. Финкельштейн М.И. Основы радиолокации: Учебник для вузов. М.: Радио и связь, 1983. 536 с.

7. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли: Учебное пособие для вузов / Под ред. Г.С. Кондратенкова. М.: Радиотехника, 2005. 368 с.

Способ формирования трехмерного изображения земной поверхности в бортовой доплеровской РЛС с линейной антенной решеткой, заключающийся в формировании на заданном промежутке времени синтезирования радиолокационного изображения участка земной поверхности в виде совокупности комплексных амплитуд S ˙ q ( i , j ) сигналов отражения в i-x элементах разрешения дальности R_i (i=1, 2, …, m, где m - число элементов дальности) на j-x частотах (j=1, 2, …, N, где N - число элементов разрешения по частоте) одновременно в Q измерительных каналах ( q = 1, Q ¯ , где q - номер канала), определении тех j-x частот, на которых амплитуда A q ( i , j ) = | S ˙ q ( i , j ) | сигнала S ˙ q ( i , j ) превышает порог обнаружения во всех каналах, и последующей обработке полученных измерений S ˙ q ( i , j ) , q = 1, Q ¯ , отличающийся тем, что при переднебоковом обзоре вектор скорости движения носителя РЛС устанавливают в горизонтальное положение, при котором элемент разрешения по доплеровской частоте однозначно определяет оценку x_ij координаты x в горизонтальной плоскости для i,j-го элемента отражения земной поверхности, а для определения оценки y_ij координаты y в вертикальной плоскости приемные элементы линейной антенной решетки (АР) располагают вдоль оси у и ориентируют их так, чтобы биссектрисы диаграмм направленности (ДН) q-x приемных элементов АР были смещены по углу места θ последовательно на величину шага h_θ=Δ_θ/(Q-1), где Δ_θ - ширина ДН на уровне 0,5 мощности, при этом для каждой совокупности полученных комплексных измерений S ˙ q ( i , j ) , q = 1, Q ¯ , определяют модули A q = | S ˙ q ( i , j ) | и получают распределение амплитуд A_q, q = 1, Q ¯ , с шагом h_θ, затем в последовательности амплитуд выбирают максимальную по q амплитуду, и соответствующий ей номер q дает начальную оценку угла места θ=-Δ_θ/2+(q-1)h_θ, которая уточняется по трем значениям амплитуд A_q-1, A_q, A_q+l методом параболической интерполяции в сторону точки максимума и дает оценку y_ij=R_isinθ, указанные операции повторяют на множестве значений i, j и получают совокупность пространственных координат x_ij, y_ij, z_ij, z i j = R i 2 − x i j 2 − y i j 2 , представляющих трехмерное изображение участка земной поверхности.