Способ визуализации ротационного искривления решетки нанотонких кристаллов

Способ визуализации ротационного искривления решетки нанотонких кристаллов

Иллюстрации

Показать все

Реферат

Изобретение относится к области электронно-микроскопической диагностики реальной структуры нанотонких кристаллов, а именно к визуализации внутреннего строения исследуемых объектов, и может быть использовано при исследовании реальной структуры наноматериалов.

Характерной особенностью реальной структуры нанотонких кристаллов является ротационное искривление их решетки. При этом искривлен не сам кристалл как целое, а искривлена только его решетка (Т.2: Наночастицы и наноструктурные функциональные покрытия / Под общ. ред. И.М. Неклюдова, В.М. Шулаева. - Харьков: ННЦ ХФТИ, 2008, с. 18-23).

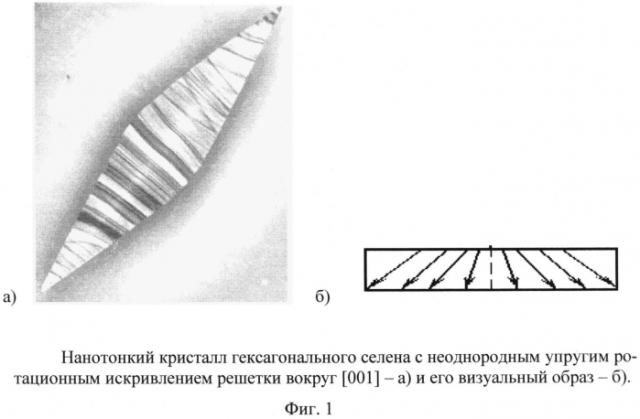
Наиболее близким является способ наглядного представления ротационного искривления решетки нанотонкого кристалла гексагонального селена вокруг [001]. Выбирается сечение ромбовидного кристалла плоскостью в направлении, перпендикулярном [001], проходящее через длинную диагональ ромба. В сечении кристалла ротационное искривление решетки вокруг оси "С" отображается путем прогрессирующего поворота стрелок, совпадающих с определенным кристаллографическим направлением, по мере удаления от центра кристалла к его периферии (фиг. 1) (Bolotov I.Е., Kolosov V.Yu. and Malkov V.В. Electron Microscopy Investigation of Crystals Based on Bend-Contour Arrangement 3. Formation of Subgrain Boundaries in Dislocation-Free Crystals of Selenium // Phys. Stat. Sol. (a). 1986, V. 95, P. 377-383).

Применение такого способа наглядного представления ротационного искривления решетки для нанотонких кристаллов гексагонального селена с решеткой, искривленной ротационным образом вокруг двух взаимно перпендикулярных направлений, возможно, но является сложным и не позволяет создать визуальный образ ротационного искривления решетки всего нанотонкого кристалла. Действительно, в связи с изменением удельной скрученности решетки ромбовидного кристалла не только вдоль направления длинной диагонали ромба, но и вдоль направления, совпадающего с короткой диагональю ромба, необходима серия из двух взаимно перпендикулярных сечений кристалла. К указанному выше сечению кристалла добавляется сечение, ему перпендикулярное и совпадающее по направлению с короткой диагональю ромба. В каждом из серии сечений вышеуказанным способом нужно отображать ротационное искривление решетки нанотонкого ромбовидного кристалла вокруг одного из двух взаимно перпендикулярных направлений - вокруг [001] и направления, совпадающего с длинной диагональю ромбовидного кристалла. Таким образом, недостатком данного способа наглядного представления ротационного искривления решетки нанотонкого кристалла является его сложность и малая наглядность, не позволяющая создать визуальный образ ротационного искривления решетки всего нанотонкого кристалла.

Задачей предлагаемого технического решения является разработка более простого и более наглядного способа визуализации, ротационного искривления решетки нанотонкого кристалла, позволяющего создавать визуальный образ всего нанотонкого кристалла.

Поставленная задача решена в предлагаемом способе визуализации ротационного искривления решетки нанотонких кристаллов, включающем получение электронно-микроскопического изображения нанотонкого кристалла в светлом и темном поле, получение электронограммы от кристалла, микродифракционное исследование, анализ картины изгибных экстинкционных контуров, присутствующих на электронно-микроскопическом изображении кристалла, расчет углов поворота решетки кристалла вокруг [001], в котором проводят микродифракционное исследование реальной структуры нанотонкого кристалла с ротационным искривлением решетки, анализ габитуса кристалла, анализ изменения радиуса изгиба его решетки с помощью формул 1.1, 1.2:

где N^(β) - расстояние между двумя произвольными контурами U₁V₁W₁ и U₂V₂W₂ на электронно-микроскопическом изображении кристалла;

r - радиус изгиба цилиндрически изогнутой решетки кристалла;

φ_UVW - угол, на который необходимо повернуть обратную решетку, чтобы узел UVW пересек сферу отражений и соответствующий изгибной контур появился на электронно-микроскопическом изображении кристалла;

β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки;

γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке;

где M^(β) - расстояние между средними линиями пар контуров и на электронно-микроскопическом изображении кристалла;

r - радиус изгиба цилиндрически изогнутой решетки кристалла;

β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки;

γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке;

и затем проводят расчет углов поворота решетки кристалла вокруг направлений ротационного искривления решетки, и на основании всей совокупности полученных экспериментальных данных осуществляют построение двумерного геометрического объекта, позволяющего создать визуальный образ ротационного искривления решетки всего нанотонкого кристалла, - поверхности ориентировок выбранного кристаллографического направления нанотонкого кристалла.

Сущность заявленного способа визуализации ротационного искривления решетки нанотонких кристаллов заключается в следующем. Для создания визуального образа ротационного искривления решетки всего нанотонкого кристалла с ротационным искривлением решетки, в общем случае вокруг двух взаимно перпендикулярных направлений, введем в рассмотрение геометрический объект - поверхность искривления решетки для определенного кристаллографического направления. Построение поверхности искривления решетки проводят следующим образом. Поверхность нанотонкого кристалла разбивают произвольным образом на элементы с площадью dS, которую устремим к нулю. Каждый элемент с площадью dS ориентируют таким образом, чтобы он был перпендикулярен исследуемому кристаллографическому направлению. Затем для каждого из элементов строят перпендикулярные им векторы, изначально (т.е. в кристалле без ротационного искривления решетки) параллельные выбранному кристаллографическому направлению и имеющие одинаковую длину. Геометрическое место концов данных векторов образует поверхность искривления решетки для выбранного авторами кристаллографического направления.

Для определения углов поворота dS используют методы электронной микроскопии:

1. метод микродифракции;

2. методы светлого и темного поля;

3. метод изгибных экстинкционных контуров.

Для использования предлагаемого способа проводят индицирование изгибных контуров, то есть определение индексов плоскостей, обусловливающих появление соответствующего изгибного контура на электронно-микроскопическом изображении кристалла. Индицирование контуров проводят с помощью методов светлого и темного поля. Получение темнопольного изображения того или иного контура осуществляют путем наклона осветительной системы, поскольку при этом достигается меньшая сферическая аберрация, чем при смещении апертурной диафрагмы.

После индицирования изгибных контуров и фиксации необходимых электронно-микроскопических изображений кристаллов и электронограмм от них на фотоматериале с помощью формул метода изгибных контуров определяют параметры изгиба и ориентировки кристалла:

где N^(β) - расстояние между двумя произвольными контурами U₁V₁W₁ и U₂V₂W₂ на электронно-микроскопическом изображении кристалла;

M^(β) - расстояние между средними линиями пар контуров и на электронно-микроскопическом изображении кристалла;

r - радиус изгиба цилиндрически изогнутой решетки кристалла;

- угловое расстояние, в исследуемом кристалле, между участками, где параллельно электронному пучку располагаются плоскости (H_xK_xL_x) и (UVW);

φ^(β) - угловое расстояние между средними линиями пар контуров и ;

β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки.

Угловое расстояние между участками, где параллельно электронному пучку располагаются плоскости (H_xK_xL_x) и (UVW), связано с угловым расстоянием между средними линиями пар контуров и соотношением:

где φ^(β) определяется из уравнения:

а Δφ - из уравнения:

где γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке, a φ_UVW - угол, на который необходимо повернуть обратную решетку, чтобы узел UVW пересек сферу отражений и соответствующий изгибной контур появился на электронно-микроскопическом изображении кристалла.

Метод изгибных контуров позволяет достигать локальности, недоступной при использовании микродифракции, и точности не менее одного градуса.

Новый технический результат, достигаемый предлагаемым способом, заключается в визуализации ротационного искривления решетки нанотонкого кристалла путем построения геометрического объекта - поверхности искривления решетки для выбранного кристаллографического направления нанотонкого кристалла с ротационным искривлением решетки, на основании экспериментальных данных, полученных при исследовании реальной структуры нанотонкого кристалла не только с помощью исследования изгибных экстинкционных контуров, светлого и темного поля, но и микродифракцией исследования реальной структуры нанотонкого кристалла с ротационным искривлением решетки и анализа изменения радиуса изгиба решетки нанотонкого кристалла с помощью формул 1.1, 1.2 и анализа габитуса кристалла, позволяющего получить визуальный образ ротационного искривления решетки всего нанотонкого кристалла.

Предлагаемый способ иллюстрируется следующими примерами.

Пример 1.

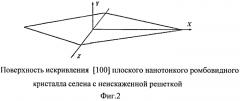
Поверхность искривления решетки для любого кристаллографического направления в идеальном монокристалле будет плоской и будет иметь форму соответствующей поверхности монокристалла. Для ромбовидного монокристалла гексагонального селена поверхность ориентировок [100] в том случае, если [100] перпендикулярно поверхности кристалла представляет собой плоский ромб. На фиг. 2 представлена поверхность искривления [100] ромбовидного монокристалла гексагонального селена, ось "С" которого ориентирована параллельно короткой диагонали ромба, а направление [100] ориентировано перпендикулярно поверхности кристалла. Радиус изгиба такой поверхности в любой ее точке r=∞, а кривизна k=0.

При температуре изотермического отжига до 160°C в аморфной пленке селена растут нанотонкие ромбовидные кристаллы, на электронно-микроскопическом изображении которых наблюдается картина изгибных экстинкционных контуров, параллельных короткой диагонали ромбовидного кристалла изгибных экстинкционных контуров. В процессе микродифракционных исследований данного кристалла были получены микроэлектронограммы, представленные на фиг. 3. Микроэлектронорамма на фиг. 3а получена от центральной части кристалла. Микроэлектронограмма на фиг. 3б получена от правой части нанотонкого кристалла. По стандартным кристаллографическим формулам проведен расчет межплоскостных расстояний, расчет осей зон. Результаты расшифровки микроэлектронограмм показаны в таблицах 1 и 2. Как следует из результатов расшифровки микроэлектронограмм, в центральной части нанотонкого кристалла в отражающем положении находятся призматические плоскости первого рода, а в периферийной части кристалла - призматические плоскости второго рода. Угол между данными плоскостями составляет тридцать градусов. Таким образом, результаты микродифракционного исследования показывают, что решетка данных кристаллов испытывает упругое ротационное искривление вокруг [001], совпадающего по направлению с короткой диагональю ромба.

Анализ картины изгибных контуров позволяет сделать вывод, что решетка нанотонкого кристалла гексагонального селена (фиг. 4) испытывает упругое ротационное искривление вокруг [001], что совпадает с выводом, полученным по результатам микродифракционного исследования нанотонкого кристалла. Так как любой изгибной экстинкционный контур является геометрическим местом точек на электронно-микроскопическом изображении нанотонкого кристалла, где соответствующая изгибному контуру плоскость кристалла находится в отражающем положении, то угол поворота решетки одинаков вдоль соответствующего изгибного контура. С учетом того что изгибные контуры параллельны короткой диагонали ромбовидного кристалла (фиг. 4), угол поворота решетки является одинаковым вдоль любого контура, параллельного короткой диагонали ромба.

С помощью формул способа изгибных экстинкционных контуров (1.3-1.6) определяют углы поворота решетки кристалла вокруг [001] и делают вывод о ее прогрессирующем ротационном искривлении при смещении от центра кристалла к его периферии, вдоль длинной диагонали ромбовидного кристалла. В зависимости от характера ротационного искривления решетки, однородное или неоднородное, в соответствии с изложенным выше способом построены поверхности ориентировок [100] (фиг. 5, 6). Радиус изгиба поверхности искривления [100] на фиг. 5 в любой ее точке является постоянным r=const, соответственно, и кривизна k=const. Радиус изгиба поверхности искривления [100] и кривизна поверхности ориентировок [100] на фиг. 6 являются постоянными в любой ее точке (r=const и кривизна k=const), но только вдоль направления OZ. В направлении ОХ r≠const и k≠const. При этом радиус возрастает, а кривизна убывает по мере удаления от центра кристалла.

Понижение температуры изотермического отжига до 160°C приводит к росту в аморфных пленках селена ромбовидных кристаллов с линейной веерообразной картиной изгибных контуров (фиг. 7) на их электронно-микроскопическом изображении.

Комплексное применение методов микродифракции, светлого и темного поля, изгибных экстинкционных контуров позволяет определить, что решетка нанотонкого кристалла с линейной веерообразной картиной изгибных контуров на электронно-микроскопическом изображении (фиг. 7) испытывает неоднородное упругое ротационное искривление вокруг двух взаимно перпендикулярных направлений - вокруг [001] и вокруг направления, лежащего в плоскости пленки и совпадающего с длинной диагональю ромбовидного кристалла и определить параметры ротационного искривления решетки нанотонкого кристалла.

Построение поверхности искривления [100] для кристаллов с линейной веерообразной картиной изгибных контуров (фиг. 7) проводят, если принять во внимание следующее обстоятельство. Исходной, реальной структурой для формирования реальной структуры кристаллов с решеткой, искривленной вокруг двух взаимно перпендикулярных направлений, является структура кристалла с неоднородным упругим ротационным искривлением решетки вокруг [001]. Следовательно, исходным состоянием поверхности искривления [100] данных кристаллов является поверхность искривления [100] кристалла с неоднородным упругим ротационным искривлением решетки вокруг [001] - поверхность искривления приведена на рис. 6. Радиус ротационного искривления решетки таких кристаллов вокруг [001], следовательно, и радиус изгиба поверхности искривления [100] линейно изменяются в направлении [001], возрастая в направлении раскрытия "веера" изгибных контуров. Действительно, в направлении раскрытия веера контуров происходит одновременное увеличение межконтурных расстояний и для пар контуров, отличающихся только знаком, и между центрами пар контуров с разными индексами. Рассмотрим, каким образом должны меняться параметры изгиба кристаллической решетки кристалла для реализации такого изменения межконтурных расстояний на электронно-микроскопическом изображении.

Для этого преобразуем выражение (1.3) таким образом, чтобы они явно зависели от величины угла β - угла между плоскостью обратной решетки, узлы которой соответствуют наблюдаемым отражениям, и плоскостью пленки. Выражение для расстояния между парой контуров, отличающихся только знаками, приобретает вид:

где N^(β) - расстояние между двумя произвольными контурами U₁V₁W₁ и U₂V₂W₂ на электронно-микроскопическом изображении кристалла;

r - радиус изгиба цилиндрически изогнутой решетки кристалла;

φ_UVW - угол, на который необходимо повернуть обратную решетку, чтобы узел UVW пересек сферу отражений и соответствующий изгибной контур появился на электронно-микроскопическом изображении кристалла;

β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки;

γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке.

Выражение для расстояния между центрами пар контуров с разными индексами, приобретает вид:

где M^(β) - расстояние между средними линиями пар контуров и на электронно-микроскопическом изображении кристалла;

r - радиус изгиба цилиндрически изогнутой решетки кристалла;

β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки;

γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке.

Анализ полученных формул показывает, что при изменении угла β расстояния N^(β) и M^(β) изменяются не одинаково. Если N^(β) уменьшается, то M^(β) увеличивается. Такое изменение межконтурных расстояний не соответствует наблюдаемым изменениям межконтурных расстояний. С учетом выражения (1.1) и (1.2) видно, что объяснение наблюдаемого изменения межконтурных расстояний обусловлено изменением величины радиуса изгиба решетки ŕ вдоль направления наименьшей скорости роста.

Получим выражения для радиуса изгиба решетки из выражений (1.1) и (1.2) для изгибного контура с индексами 202 при β=10°, ctgγ=0,772 и sin φ_UVW=0,02:

Действительно, при линейном изменении ŕ, а именно при линейном увеличении расстояний в направлении раскрытия "веера" контуров, происходит изменение межконтурных расстоянии и линейно увеличиваются и N^(β) и M^(β), что совпадает с наблюдаемой картиной поведения изгибных контуров. Измеряя N^(β) и М^(β) на электронно-микроскопическом изображении кристалла с учетом увеличения, можно получить значения радиуса изгиба решетки (табл. 3).

Соответственно, линейно изменяется кривизна поверхности искривления [100], уменьшаясь в направлении раскрытия "веера" контуров. Вдоль направления, перпендикулярного [001], радиус и кривизна поверхности искривления решетки данных кристаллов изменяются также, как изменяются радиус и кривизна поверхности искривления [100] в направлении, перпендикулярном [001] кристаллов с неоднородным упругим ротационным искривлением вокруг [001], а именно радиус монотонно возрастает, а кривизна монотонно убывает по мере удаления от центра кристалла в указанном направлении. Поверхность ориентировок [100], построенная с учетом перечисленных обстоятельств, показана на фиг. 8 и испытывает конический изгиб. Геометрия всех представленных выше поверхностей ориентировок [100] - плоской, цилиндрической, испытывающей круговой и некруговой изгиб, конический изгиб, является евклидовой геометрией.

Пример 2.

При температуре изотермического отжига 150°С в аморфных пленках селена растут ромбовидные кристаллы, на электронно-микроскопическом изображении которых наблюдается нелинейная веерообразная система изгибных контуров (фиг. 9).

С учетом выражения (1.1) и (1.2) видно, что объяснение наблюдаемого изменения межконтурных расстояний обусловлено изменением величины радиуса изгиба решетки - ŕ вдоль направления наименьшей скорости роста. Получим выражения для радиуса изгиба решетки из выражений (1.5) и (1.6) для изгибного контура с индексами 201 при β=10°, ctgγ=0,387 и sin φ_UVW=0,029:

Действительно, при нелинейном изменении ŕ, а именно при нелинейном увеличении в направлении раскрытия "веера" контуров, происходит изменение межконтурных расстояний и нелинейно увеличиваются N^(β) и М^(β), что совпадает с наблюдаемой картиной поведения изгибных контуров. Измеряя N^(β) и М^(β) на электронно-микроскопическом изображении кристалла с учетом увеличения, можно получить значения радиуса изгиба решетки (Табл. 4).

Принимая во внимание выражения (1.9, 1.10), видно, что при нелинейном изменении N^(β) и М^(β) и радиус ротационного искривления решетки, и радиус изгиба поверхности искривления [100] вокруг [001] в таких кристаллах нелинейно изменяется в направлении [001], возрастая в направлении раскрытия "веера" изгибных контуров. Соответственно, нелинейно изменяется и кривизна изгиба поверхности ориентировок [100] таких кристаллов вокруг [001], уменьшаясь в направлении раскрытия "веера" контуров.

Как следует из результатов электронно-микроскопических исследований эволюции реальной структуры нанотонких кристаллов селена, исходной реальной структурой для формирования реальной структуры ромбовидных кристаллов с нелинейной веерообразной картиной контуров на их электронно-микроскопическом изображении является реальная структура ромбовидных кристаллов, на электронно-микроскопическом изображении которых наблюдается линейная веерообразная картина изгибных контуров. Отсюда следует, что поверхность искривления [100] ромбовидных кристаллов с линейной веерообразной картиной контуров на их электронно-микроскопическом изображении (фиг. 8) является исходной поверхностью для построения поверхности искривления [100] для ромбовидных кристаллов с нелинейной веерообразной картиной изгибных экстинкционных контуров на их электронно-микроскопическом изображении (фиг. 9).

Нелинейная веерообразная картина изгибных контуров с увеличением нелинейности - все большего отклонения изгибных контуров от направления, параллельного [001] к направлению [100], является следствием появления второй оси изгиба решетки нанотонкого кристалла селена - ротации оси "С" вокруг направления [100]. Решетка ромбовидных кристаллов с нелинейной, веерообразной картиной изгибных контуров, испытывает неоднородное упругое ротационное искривление вокруг двух взаимно перпендикулярных направлений. Во-первых, вокруг оси "С" и, во-вторых, вокруг перпендикулярного ей направления - оси ОХ. В процессе роста происходит качественное изменение характера упругого ротационного искривления решетки нанотонкого кристалла селена и, соответственно, происходит качественное изменение свойств поверхности ориентировок [100] (фиг. 10).

Действительно, свойства поверхности, изогнутой вокруг двух взаимно перпендикулярных направлений, в отличие от поверхности изогнутой вокруг одного направления, описываются уже не с помощью нормальной кривизны, а с помощью гауссовой кривизны:

Геометрия поверхности, гауссова кривизна которой отлична от нуля, принципиально отличается от геометрии поверхности, гауссова кривизна которой равна нулю. Поскольку любая поверхность, изогнутая вокруг двух взаимно перпендикулярных направлений, представляет собой двумерное риманово пространство и, соответственно, ее геометрия является римановой, постольку и геометрия рассматриваемой поверхности искривления [100] является римановой (Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967, с. 553-559). В этом случае гауссова кривизна совпадает с римановой кривизной поверхности. Поскольку поверхность искривления [100] является не чем иным как геометрическим образом плоскостей кристалла (100), то понятно, что в результате изменения характера упругого ротационного искривления решетки нанотонкого кристалла селена от ротационного искривления решетки вокруг одного направления к ротационному искривлению решетки вокруг двух взаимно перпендикулярных направлений происходит изменение геометрии плоскостей кристалла типа (100). Указанные плоскости кристалла в процессе деформации искажаются, эволюционируя в поверхности с отличной от нуля римановой кривизной, совпадающей по величине с гауссовой кривизной. Геометрия плоскостей решетки нанотонкого кристалла селена, искаженных в процессе деформации и эволюционировавших в поверхности, эволюционирует от евклидовой геометрии к римановой.

Таким образом, построение и изучение поверхностей искривления решетки для нанотонких кристаллов селена, растущих в аморфных пленках при различных температурах изотермического отжига, позволяют получить визуальный образ всего нанотонкого кристалла и, тем самым, позволюет выявить эволюцию геометрии поверхности искривления решетки от евклидовой к римановой. В результате выявляется соответствующее изменение геометрии кристаллических “плоскостей” нанотонкого кристалла селена от евклидовой к римановой.

Приведенные примеры построения поверхностей искривления решетки для выделенного кристаллографического направления нанотонких кристаллов гексагонального селена с ротационным искривлением решетки, на основании экспериментальных данных, полученных при исследовании реальной структуры нанотоких кристаллов с помощью различных способов исследования, показывают возможность визуализации ротационного искривления решетки всего нанотонкого кристалла в соответствии с заявляемым способом.

Заявленный способ визуализации ротационного искривления решетки нанотонкого кристалла позволяет на основании экспериментальных данных, полученных при исследовании реальной структуры нанотонкого кристалла, построить двумерный геометрический объект - поверхность искривления решетки для выбранного кристаллографического направления, и характеризуется простотой и исключительной наглядностью. Именно простота и наглядность заявляемого способа позволяют не только визуализировать ротационное искривление решетки нанотонкого кристалла, но и визуализировать изменение геометрии решетки нанотонких кристаллов от евклидовой к римановой.

Способ визуализации ротационного искривления решетки нанотонких кристаллов, включающий получение электронно-микроскопического изображения нанотонкого кристалла в светлом и темном поле, получение электронограммы от кристалла, микродифракционное исследование, анализ картины изгибных экстинкционных контуров, присутствующих на электронно-микроскопическом изображении кристалла, расчет углов поворота решетки кристалла вокруг [001], отличающийся тем, что проводят микродифракционное исследование реальной структуры нанотонкого кристалла с ротационным искривлением решетки, анализ габитуса кристалла, анализ изменения радиуса изгиба его решетки с помощью формул 1.1, 1.2: где N^(β) - расстояние между двумя произвольными контурами U₁V₁W₁ и U₂V₂W₂ на электронно-микроскопическом изображении кристалла;r - радиус изгиба цилиндрически изогнутой решетки кристалла;φ_UVW - угол, на который необходимо повернуть обратную решетку, чтобы узел UVW пересек сферу отражений и соответствующий изгибной контур появился на электронно-микроскопическом изображении кристалла;β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки;γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке; где M^(β) - расстояние между средними линиями пар контуров и на электронно-микроскопическом изображении кристалла;r - радиус изгиба цилиндрически изогнутой решетки кристалла;β - угол отклонения плоскости обратной решетки, узлы которой соответствуют наблюдаемым отражениям, от положения, параллельного плоскости пленки;γ - угол между нормалями к плоскостям (H_xK_xL_x) и (UVW) в прямой решетке;и затем проводят расчет углов поворота решетки кристалла вокруг направлений ротационного искривления решетки, и на основании всей совокупности полученных экспериментальных данных осуществляют построение двумерного геометрического объекта, позволяющего создать визуальный образ ротационного искривления решетки всего нанотонкого кристалла, - поверхности искривления решетки для выбранного кристаллографического направления нанотонкого кристалла.