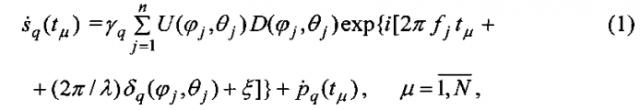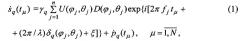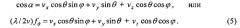Способ формирования трехмерного изображения земной поверхности в бортовой четырехканальной доплеровской рлс

Способ формирования трехмерного изображения земной поверхности в бортовой четырехканальной доплеровской рлс

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, а именно к бортовым радиолокационным системам наблюдения за земной поверхностью на базе доплеровской радиолокационной станции (РЛС) с четырехэлементной антенной решеткой (АР).

Трехмерное изображение участка земной поверхности формируется в виде совокупности пространственных координат элементов отражения земной поверхности в зоне видимости РЛС, определяемой диаграммой направленности антенны (ДНА). Наличие такого изображения позволяет повысить безопасность маловысотных полетов над сложным рельефом местности.

Известен способ измерения координат элементов земной поверхности в бортовой четырехканальной доплеровской РЛС [1], центры приемных элементов которой расположены на плоскости антенны в точках с координатами (x_l,y₁)=(d,d), (x₂,y₂)=(-d,d), (x₃,y₃)=(-d,-d), (х₄,у₄)=(d,-d), где 2d - базовое расстояние между центрами соседних элементов. Данный способ позволяет получать трехмерное изображение земной поверхности в зоне видимости РЛС, ограниченной шириной узкой (порядка 1° - 3° на уровне 0,5 мощности) круговой диаграммы направленности антенны (ДНА) при радиальной дальности R порядка 1-10 км, характерной для маловысотного полета носителя РЛС. Способ является наиболее близким по технической сути и заключается в следующем.

1. При данном положении линии визирования антенны, соответствующем переднебоковому обзору бортовой РЛС, получают комплексные траекторные сигналы S ˙ q ( t ) на заданном промежутке времени t синтезирования одновременно в q-x измерительных каналах (номер канала совпадает с номером q приемного элемента антенны: q=1,2,3,4). Затем эти сигналы селектируют в i-x элементах разрешения дальности R_i по задержке времени прихода отраженного сигнала. В результате из S ˙ q ( t ) выделяют i-е составляющие S ˙ q ( i , t ) , i=1, 2, …, m, по числу элементов дальности m.

2. В каждом i-м элементе дальности со значением R_i сигналы S ˙ q ( i , t ) преобразуют во временные последовательности S ˙ q ( i , t ) , j = 1, N ¯ (N - число временных отсчетов на промежутке синтезирования), которые подвергают дискретному преобразованию Фурье (ДПФ). Тем самым селектируют сигнал по доплеровской частоте f_j в каждом q-м канале. В результате из S ˙ q ( i , t ) выделяют j-е составляющие S ˙ q ( i , f j ) , j=1, 2 …, N, в q-x каналах, q=1, 2, 3, 4, где N становится числом элементов разрешения по частоте. Данные операции выполняют одновременно (параллельно) в 4-х каналах.

3. Из N элементов разрешения по частоте рассматривают только те n элементов (n<<N), на которых амплитуда сигнала U q ( i , j ) = | S ˙ q ( i , f j ) | превышает порог обнаружения во всех q-x каналах. Такие элементы разрешения соответствуют элементам отражения земной поверхности.

4. Оценки угловых координат φ - азимута и θ - угла места осуществляют моноимпульсным методом в антенной системе координат. А именно:

4.1) для каждой i, j-й четверки измерений S ˙ q = S ˙ q ( i , f j ) , q=1, 2, 3, 4, вычисляют комплексный суммарный S ˙ Σ и комплексные разностные сигналы S ˙ ϕ , S ˙ θ по формулам:

S ˙ Σ = S ˙ 1 + S ˙ 2 + S ˙ 3 + S ˙ 4 , S ˙ ϕ = S ˙ 2 + S ˙ 3 − S ˙ 1 − S ˙ 4 , S ˙ θ = S ˙ 3 + S ˙ 4 − S ˙ 1 − S ˙ 2 ;

4.2) выделяют действительную часть суммарного сигнала Re { S ˙ Σ } , мнимые части разностных сигналов Im { S ˙ ϕ } , Im { S ˙ θ } и вычисляют пеленгационные характеристики:

U ϕ = − Im { S ˙ ϕ / S ˙ Σ } , U θ = − Im { S ˙ θ / S ˙ Σ } ;

4.3) находят угловые координаты центра элемента отражения по формулам:

φij=kU_φ, θij=kU_θ, k=λ/(2πd),

где λ - длина волны;

4.4) вычисляют прямоугольные координаты центров i,j-х элементов отражения земной поверхности для узкой ДНА по формулам:

x_ij=φ_ijRi, y_ij=θ_ijR_i, z_i=R_i.

5. Совокупность координат x_i,j, y_ij, z_i, полученных на множестве значений i,j, дает трехмерное изображение земной поверхности по ширине ДНА, которое отображается на экране индикатора пилота летательного аппарата. Однако данный способ обладает следующими недостатками: 1) точность измерения координат моноимпульсным методом ниже, чем точность измерения координат фазовым методом (фазовый метод, например, [2, с. 424]);

2) область обзора РЛС ограничена шириной узкой ДНА порядка 1° - 3°.

Технический результат направлен на формирование трехмерного изображения поверхности в зоне видимости РЛС с устранением указанных недостатков, а именно на повышение точности определения пространственных координат и расширение зоны видимости РЛС.

Технический результат предлагаемого технического решения достигается тем, что способ формирования трехмерного изображения земной поверхности в бортовой четырехканальной доплеровской РЛС заключается в формировании на заданном промежутке времени синтезирования радиолокационного изображения участка земной поверхности в виде совокупности комплексных амплитуд S ˙ q ( i , j ) сигналов отражения в i-x элементах разрешения дальности R_i (i=1, 2,…, m, где m - число элементов дальности) на j-x частотах (j=1, 2,…, N, где N - число элементов разрешения по частоте) одновременно в четырех измерительных каналах (q=1, 2, 3, 4, где q - номер канала), определении тех j-x частот, на которых амплитуда U q ( i , j ) = | S ˙ q ( i , j ) | сигнала S ˙ q ( i , j ) превышает порог обнаружения во всех каналах, и последующей обработке полученных измерений S ˙ q ( i , j ) , отличающийся тем, что центры приемных элементов антенны располагают на плоскости антенны в точках с координатами (x_l,y_l)=(d,0), (x₂,y₂)=(0,d), (x₃,y₃)=(-d,0), (х₄,y₄)=(0,-d), и для каждой i,j-й четверки измерений S ˙ q = S ˙ q ( i , j ) , q=1, 2, 3, 4, полученных в q-x каналах, берут аргументы комплексных величин S ˙ q - фазы ψ q = arg { S ˙ q } , q=1, 2, 3, 4, вычисляют разности фаз по азимуту φ и углу места θ: Δψ_φ=ψ₁-ψ₃, Δψ_θ=ψ₂-ψ₄ и находят прямоугольные координаты точек отражения:

x_ij=kΔψ_φ, y_ij=kΔψ_θ, z i j = R i 2 − x i j 2 − y i j 2 ≈ R i , k=R_iλ/(4πd), λ - длина волны, которые на множестве значений i,j дают трехмерное изображение участка земной поверхности по ширине узкой ДНА, затем смещают линию визирования антенны последовательно по азимуту и углу места на ширину ДНА и повторяют указанные операции. Способ осуществляют следующим образом.

1. Центры приемных элементов антенны располагают на плоскости антенны в точках с координатами (x_l,y₁)=(d,0), (x₂,y₂)=(0,d), (x₃,y₃)=(-d,0), (x₄,y₄)=(0,-d), где 2d - базовое расстояние между центрами приемных элементов, расположенных на одной оси.

2. При данном положении линии визирования антенны, соответствующем переднебоковому обзору бортовой РЛС, получают комплексные траекторные сигналы S ˙ q ( t ) на заданном промежутке времени t синтезирования одновременно в q-x каналах: горизонтальных (для 1-го и 3-го приемных элементов) и вертикальных (для 2-го и 4-го приемных элементов).

3. Сигналы S ˙ q ( t ) селектируют в i-x элементах разрешения дальности R_i по задержке времени прихода отраженного сигнала. В результате из S ˙ q ( t ) выделяют i-е составляющие S ˙ q ( i , t ) , i=1, 2,…, m, по числу элементов дальности m.

4. В каждом i-м элементе дальности со значением R_i сигналы S ˙ q ( i , t ) преобразуют во временные последовательности S ˙ q ( i , t j ) , j = 1, N ¯ (N - число временных отсчетов на промежутке синтезирования), которые подвергают дискретному преобразованию Фурье (ДПФ). Тем самым селектируют сигнал по доплеровской частоте f_j в каждом q-м канале. В результате из S ˙ q ( i , t ) выделяют j-е составляющие S ˙ q ( i , f j ) , j=1, 2 …, N, в q-x каналах, q=1, 2, 3, 4, где N становится числом элементов разрешения по частоте. Данные операции выполняют одновременно (параллельно) в 4-х каналах.

5. Из N элементов разрешения по частоте рассматривают только те n элементов (n<<N), на которых амплитуда сигнала U q ( i , j ) = | S ˙ q ( i , f j ) | превышает порог обнаружения во всех q-x каналах. Такие элементы разрешения соответствуют элементам отражения земной поверхности.

6. Для каждой i,j-й четверки измерений S ˙ q = S ˙ q ( i , f j ) , q=1, 2, 3, 4, находят пространственные координаты i,j-го отражающего элемента, а именно:

6.1) берут аргументы комплексных величин S ˙ q - фазы ψ q = arg { S ˙ q } , q=1, 2, 3, 4 и вычисляют разности фаз по азимуту φ для горизонтальных каналов (1 и 3) и по углу места θ для вертикальных каналов (2 и 4):

Δψ_φ=ψ₁-ψ₃, Δψ_θ=ψ₂-ψ₄;

6.2) для полученных разностей фаз находят оценки угловых координат:

φ_ij=kΔψ_φ, θ_ij=kΔψ_θ, k=λ/(4πd).

6.3) оценки угловых координат пересчитывают в пространственные прямоугольные координаты, которые для узкой ДНА вычисляют по формулам:

x_ij=φ_ijR_i, y_ij=θ_ijR_i, z i j = R i 2 − x i j 2 − y i j 2 ≈ R i .

Совокупность координат x_ij, y_ij, x_ij на множестве значений i,j дает трехмерное изображение участка земной поверхности по ширине ДНА.

7. Линию визирования антенны последовательно смещают по азимуту и углу места на ширину ДНА и повторяют операции пп. 2-6. В результате получают трехмерное изображение земной поверхности в расширенной зоне видимости РЛС.

Расчетная часть

Модель временной последовательности s ˙ q ( t μ ) , µ=1, 2, …, N, на входе ДПФ в каждом q-м канале (q=1, 2, 3, 4) в антенной системе координат [1] имеет вид

где U(φ_j,θ_j)=ρ(φ_j,θ_j)U₀ - амплитуда сигнала от j-го отражающего элемента земной поверхности с угловыми координатами φ_j,θ_j, соответствующими j-му элементу разрешения по доплеровской частоте с частотой центра f_j; ρ - коэффициент отражения, зависящий от φ_j, θ_j; U₀ - амплитуда зондирующего сигнала; D(φ, θ) - амплитудная характеристика ДНА на излучение и прием, например:

k₀ - известный коэффициент (k₀=2,78); Δ_φ и Δ_θ - ширина ДНА по азимуту и углу места на уровне 0,5 мощности; i - мнимая единица; δ_q(φ,θ) - запаздывание или опережение по фазе принимаемого отраженного сигнала от элемента с угловыми координатами φ,θ в q-м приемном элементе антенны по сравнению с центром антенны; ξ - составляющая фазы в элементе разрешения дальности: ξ=-4πR/λ+ϕ₀+η; ϕ₀ - начальная фаза; η - случайная величина, равномерно распределенная на [0,2π] и описывающая неопределенность отражения в элементе дальности (η меняет свое значение по элементам дальности); ρ ˙ q ( t μ ) комплексный белый шум с нулевым средним (шум аппаратуры) и дисперсией σ p 2 ; γ_q - мультипликативная помеха с единичным средним, моделирующая флуктуации сигналов в q-x каналах.

Суммирование в (1) ведется по n элементам разрешения доплеровской частоты, соответствующим n последовательно расположенным элементам отражения земной поверхности в пределах ширины ДНА в данном элементе разрешения дальности R. Отсчет времени t_µ ведется с частотой дискретизации f_д, обеспечивающей отсутствие "растекания частот" при ДПФ, т.е. для каждой частоты f_j выполняется равенство: f_j=qf_д/N, где q - целое.

Величина δ_q(φ,θ) определяется как разность расстояний: δ_q=R-R_q, где R - удаление центра отражающего элемента поверхности с координатами x,y,z от центра антенны; R - удаление центра этого же элемента от центра q-го приемного элемента антенны с известными координатами х_q, у_q и z_q=0. Для практического расчета δ_q примем допущение. Представим сферический фронт отраженной волны, достигшей центрального элемента антенны, касательной плоскостью (плоским фронтом) с нормальным вектором n → = ( x , y , z ) = R ( cos θ sin ϕ ,   sin θ ,   cos θ cos ϕ ) . Или ортом вектора нормали n → 0 = ( cos θ sin ϕ ,   sin θ ,   cos θ cos ϕ ) , совпадающим с ортом радиус-вектора r → = ( x , y , z ) точки M(x,y,z) - центра элемента отражения. Считаем, что плоский фронт волны с таким же нормальным вектором достигает центра остальных приемных элементов антенны. Тогда величина δ_q определится как отклонение центра q-го приемного элемента (точки с координатами x_q,y_q,0) от плоскости, проходящей через начало координат с вектором нормали n → 0 , по формуле: δ_q=x_qcosθsinφ+y_qsinθ, или с учетом cosθsinφ=x/R, sinθ=y/R:

Формула (3) дает линейную зависимость δ_q от x, у при известном R. Для указанных ранее координат центров приемных элементов антенны

Связь угловых φ,θ и соответственно прямоугольных х,у координат с доплеровской частотой f_д получается следующим образом. Для режима доплеровского обужения луча (ДОЛ) имеем [3, с. 22, с. 52]: f_д=(2v/λ)cosα, где cosα находится с помощью скалярного произведения двух векторов: v → 0 = ( v x , v y , v z ) - орта вектора скорости v → движения носителя РЛС и r → 0 = ( cos θ sin ϕ ,   sin θ ,   cos θ cos ϕ ) - орта радиус-вектора r → = ( x , y , z ) точки отражения:

Уравнение (5) при фиксированных v и f_д представляет собой нелинейное уравнение линии доплеровской частоты (изодопы) на дальности R в угловых координатах φ,θ. Или линейное уравнение в прямоугольных координатах x,y,z (при фиксированном R):

(λ/2v)f_д=(v_xx+v_yy+v_zz)/R.

В результате ДПФ временные последовательности s ˙ q ( t μ ) , μ = 1, N ¯ одновременно в q-x каналах (q=1, 2, 3, 4) преобразуются в частотные последовательности s ˙ q ∗ ( f j ) , j=1, 2, …, N. Для n доплеровских частот n<<N, соответствующих отражающим элементам поверхности и расположенным в общей полосе частот ДПФ, принимается модель:

j=1, 2, …, n, где δ_q определены в (4).

Из модели (6) видно, что угловые координаты φ,θ центров отражающих элементов содержатся в амплитудной и фазовой части обрабатываемых сигналов. Причем для измеряемых фаз ψ_q=(2π/λ)δ_q+ξ их разности:

где ε₁ и ε₂ - ошибки измерения разности фаз.

Искомые координаты находятся из (7), если пренебречь ε₁ и ε₂:

При этом СКО ошибок оценивания φ, θ определится как σ ϕ = σ θ = σ ε λ 4 π d , где σ_ε - СКО ошибок ε.

Заметим, что разности фаз, взятые без учета ошибок их измерения:

где Δ_φ=δ_l-δ₃, Δ_θ=δ₂-δ₄, при малых углах φ,θ однозначно определяются величиной Δ_φ и Δ_θ. Так, если Δ_φ меняется в пределах 0≤Δ_φ≤λ, что соответствует малым углам φ,θ, разность фаз меняется в пределах 0≤Δψ_φ≤2π или -π≤ψ≤π, и между Δ_φ и Δψ_φ устанавливается однозначное соответствие (9). Однако для больших углов φ,θ возникает неоднозначность. Так, если λ<Δ_φ≤2λ, что соответствует большим углам φ,θ, Δψ_φ снова меняется в пределах 0≤Δψ_φ≤2π. То же самое при 2λ<Δ_φ≤3λ и т.д. Устранение неоднозначности решается алгоритмически и конструктивно за счет введения пятого центрального элемента антенны при несимметричном расположении остальных приемных элементов антенны по осям x и y. При этом образуются грубые и точные каналы [2, с. 424]. Однако для узкой ДНА, характерной для фазированной АР, прием сигналов ведется с направлений однозначного измерения фазы. Также не рассматривается поправка на сферичность фронта волны на указанной дальности R.

Результаты моделирования

Способ-прототип и предлагаемый способ сравнивались в условиях переднебокового обзора математическим моделированием. Скорость летательного аппарата и орт вектора скорости задавались: v=100 м/с, v → 0 = ( 1 / 2 ;   0 ;   1 / 2 ) . На дальности R=1000 м моделировалась полоса склона земной поверхности. При ширине круговой ДНА 2° на дальности R высота склона по оси oy составляла 34 м, протяженность по оси ох также 34 м. Центры элементов отражения общим числом n=25 шли с шагом 1,36 м по осям x и у в сторону уменьшения высоты склона. Оценке подлежали пространственные координаты этих центров. Зондирующие импульсы числом N=5000 при моделировании отражались от центров элементов полосы поверхности с коэффициентом ρ=1. При длине волны λ=0,01 м отраженные сигналы принимались в 4-х элементах антенной решетки с базовым расстоянием 2d=0,1 м и после прохождения тракта первичной обработки в 4-х каналах формировались в соответствии с моделью (1). При частоте дискретизации f_д=100 кГц получались 4 временные последовательности длиной N=5000 каждая, которые подвергались ДПФ. В общей полосе частот [0,100 кГц] полоса доплеровских частот, соответствующая отражающим элементам поверхности, составляла [13,9 кГц; 14,4 кГц] с разрешением по частоте 20 Гц. Полученные в результате ДПФ спектральные последовательности подавались на вход алгоритмов 1 и 2 обработки данных. Алгоритм 1 соответствовал способу-прототипу, основанному на моноимпульсном методе, алгоритм 2 - предлагаемому способу, основанному на фазовом методе. Результаты моделирования представлены ниже.

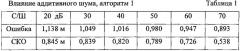
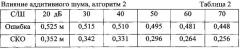
В таблицах 1, 2 показано влияние аддитивного шума ρ ˙ q ( t μ ) в модели (1) на точность работы алгоритмов 1, 2. Даны зависимости средней ошибки определения пространственных координат центров элементов отражения и оценок СКО этих ошибок от отношения сигнал-шум С/Ш=201g(U₀/σ_р).

Видно преимущество алгоритма 2 по точности определения координат. В таблицах 3, 4 показано влияние мультипликативной помехи γ_q при фиксированном отношении С/Ш=60 дБ. Действие γ_q моделировалось случайным изменением γ_q по q-м каналам с отклонением на указанный процент относительно ее среднего значения.

Видно также преимущество алгоритма 2 предложенного способа. Данный способ может найти внедрение в существующих бортовых системах наблюдения за земной поверхностью с целью повышения безопасности маловысотных полетов.

Литература

1. Положительное решение по заявке №2013119344/07(028620).

2. Финкельштейн М.И. Основы радиолокации: Учебник для вузов. М.: Радио и связь, 1983. 536 с.

3. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли: Учебное пособие для вузов / Под ред. Г.С. Кондратенкова, М.: Радиотехника, 2005. 368 с.

Способ формирования трехмерного изображения земной поверхности в бортовой четырехканальной доплеровской РЛС, заключающийся в формировании на заданном промежутке времени синтезирования радиолокационного изображения участка земной поверхности в виде совокупности комплексных амплитуд сигналов отражения в i-x элементах разрешения дальности R_i (i=1, 2, …, m, где m - число элементов дальности) на j-x частотах (j=1, 2, …, N, где N - число элементов разрешения по частоте) одновременно в четырех измерительных каналах (q=1, 2, 3, 4, где q - номер канала), определении тех j-x частот, на которых амплитуда сигнала превышает порог обнаружения во всех каналах, и последующей обработке полученных измерений , отличающийся тем, что центры приемных элементов антенны располагают на плоскости антенны в точках с координатами (x₁,y₁)=(d,0), (x₂,y₂)=(0,d), (x₃,y₃)=(-d,0), (x₄,y₄)=(0,-d) и для каждой i,j-й четверки измерений , q=1, 2, 3, 4, полученных в q-x каналах первичной обработки, берут аргументы комплексных величин - фазы , q=1, 2, 3, 4, вычисляют разности фаз по азимуту φ и углу места θ: Δψ_φ=ψ₁-ψ₃, Δψ_θ=ψ₂-ψ₄ и находят прямоугольные координаты точек отражения:x_ij=kΔψ_φ, y_ij=kΔψ_θ,, k=R_iλ/(4πd),λ - длина волны, которые на множестве значений i,j дают трехмерное изображение участка земной поверхности по ширине узкой диаграммы направленности антенны, затем смещают линию визирования антенны последовательно по азимуту и углу места на ширину диаграммы направленности и повторяют указанные операции.