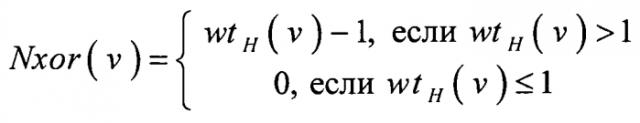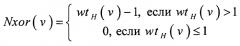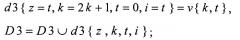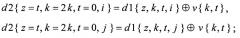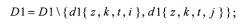Способ формирования s-блоков с минимальным количеством логических элементов

Способ формирования s-блоков с минимальным количеством логических элементов

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Предлагаемое изобретение относится к области вычислительной техники и криптографии и, в частности, к способам формирования S-блоков с минимальным количеством логических элементов для последующей реализации в устройствах защиты данных криптографическими методами.

Уровень техники

Способы формирования S-блоков с минимальным количеством логических элементов известны.

Так, известен способ, улучшающий аппаратную реализацию фиксированного шифра (стандарта криптографической защиты - AES), основанный на применении обращения по модулю неприводимых полиномов в поле GF(1ⁿ) (при этом операция по модулю неприводимых полиномов в поле GF(2ⁿ) реализуется аппаратно), известный способ относится к криптографическому устройству и может быть использован в системах защиты информации [1].

Недостатком известного способа является невозможность применения для реализации произвольных S-блоков, в том числе больших размерностей.

Наиболее близким по своей технической сущности является способ, заключающийся в том, что при записи запоминаемой информации строится функция, параметры которой устанавливают в зависимости от запоминаемой информации, информация хранится в виде схемотехнической реализации построенной функции и при считывании запоминаемая информация восстанавливается по значениям этой функции, причем по запоминаемой информации в вычислительной системе строится булевская логическая функция в совершенной нормальной дизъюнктивной форме, аргументом которой является адрес запоминаемой информации, а значением является запоминаемая информация, затем булевская логическая функция преобразуется в форму многочлена Жегалкина, далее минимизируется число элементарных булевских операций, входящих в многочлен Жегалкина, и затем минимизированный многочлен Жегалкина реализуется на различных платформах (в том числе на программируемой логической интегральной схеме - ПЛИС) [2].

Указанный способ может быть использован в более широкой области для работы с произвольной информацией, не ограниченной определенной схемотехнической реализацией, и принимается за прототип.

Недостатком этого способа является отсутствие возможности минимизации схемотехнических затрат, которое может быть выражено в количестве логических операций сложения и умножения при реализации заданного S-блока, в виде минимизированной схемы системы многочленов Жегалкина на различных платформах (в том числе на ПЛИС).

Раскрытие изобретения

Техническим результатом предлагаемого способа является уменьшение схемотехнических затрат при реализации S-блока за счет минимизации результирующей логической схемы.

Для этого предлагается способ, заключающийся в том, что

- задают исходный S-блок, имеющий n входов;

- формируют систему n булевых функций по заданному S-блоку в виде таблицы истинности;

- осуществляют умножение матрицы Адамара на значения булевых функций;

- получают n векторов, которые представляют собой значения коэффициентов полиномов Жегалкина;

- формируют множество векторов P={p₁, p₂, …, p_n}, i=1…n, компоненты которых составлены из соответствующих коэффициентов полинома Жегалкина путем замены a₀, a₁,…, a_ij,…, a_ij,…, a_1…n на a 0 , a 1 , … , a 2 n − 1 ;

- устанавливают начальные значения

k=1;

kt=0;

- формируют множество D1{z, k, t, i] векторов длины 2ⁿ (исходно пустое), где каждому вектору дополнительно сопоставлены значения z=0, t=0,

где z - номер пары векторов в предыдущей итерации k;

t - номер пары векторов в текущей итерации k;

- добавляют во множество D1 векторы

d1{z=0, k=k, t=0, i}=р_i;

- находят наиболее часто встречающиеся подпоследовательности компонент в векторах p_i, выполняя следующие действия:

- (А1) формируют исходно пустое множество DTMP {z, k, t=0, i} векторов длины n, где каждому вектору дополнительно сопоставлены значения t=0 и k=k;

- формируют исходно пустое множество D2 {z, k, t, i} векторов длины 2ⁿ;

- формируют исходно пустое множество D3 {z, k, t, i} векторов длины 2ⁿ;

- устанавливают начальное значение для номера пары

t=1;

- (А2) если выполняется соотношение

|D1{z, k, t=0, i}|<2,

то переходят к выполнению этапа A3;

- определяют пару векторов (d1{z, k, t, i}, d1{z, k, t, j}) во множестве D1 {k}, причем i≠j такую, что величина

Nxor_A(v{k, t}=d1{z, k, t, i}&d1{z, k, t, j}),

где

wt_H(v) - вес Хэмминга вектора v;

v - произольный двоичный вектор;

принимает максимальное значение;

- если Nxor_A=0 и t=1, то переходят к выполнению этапа А5;

- добавляют во множество DTMP последовательно векторы (d1{z, k, t, i},d1{z, k, t, j}) для определения пары t

- добавляют во множество D3 вектор

- удаляют из векторов каждой пары общие элементы

- добавляют во множество D2 оба вектора

- удаляют участвовавшие пары векторов из множества D1

- вычисляют

t=t+1;

- вычисляют мощность множества векторов D1

- переходят к выполнению этапа А2;

- (A3) временно сохраняют множество DTMP векторов (d1 {z, k, t, i}, d1 {z, k, t, j}) и множества векторов D2{z, k, t, i} и D3{z, k, t, i};

- вычисляют

kp=2k,

kv=2k+1;

- если выполняется соотношение

то переходят к выполнению этапа А4;

- вычисляют

k=kv;

- присваивают элементам множества D1{k} значения элементов множества D3{kv}

d1{z, k, t, i}=d3{z, kv, t, i};

- вычисляют

kt=0;

- переходят к выполнению этапа А1;

- (А4) если выполняется соотношение

|D2{z, k=kp, t, i}|<2,

то переходят к выполнению этапа А6;

- вычисляют

k=kp,

kt=1;

- присваивают элементам множества D1{z, k, t, i} значения элементов множества D2 { z, kp, t, i}

d1{z, k, t, i}=d2{z, kp, t, i};

- переходят к выполнению этапа А1;

- (А5) если kt=1, то переходят к выполнению этапа А6, иначе переходят к выполнению этапа А4;

- (А6) получают результирующую логическую функцию, выполняя следующие действия:

- вычисляют k=1;

- формируют вспомогательный вектор kf(n), изначально имеющий нулевые элементы;

- (С1) если kf(k)=1, то переходят к выполнению этапа С2;

- вычисляют

k=2k+1

- вычисляют количество векторов m в итерации k;

- если m≠0, то переходят к выполнению этапа С1;

- вычисляют

k=(k-1)/2;

- переходят к выполнению этапа С3;

- (С2) если k является четным, то

- вычисляют

k=k/2;

- переходят к выполнению этапа С3;

- вычисляют

k=k-1;

- если

k=0,

то переходят к выполнению этапа С7, иначе переходят к выполнению этапа С1;

- (С3) вычисляют количество векторов m в итерации k;

- если m=1, то

- формируют схему для вектора d1[z, k, t, i};

- переходят к выполнению этапа С6;

- вычисляют

t=1;

- (С4) если t>m/2, то переходят к выполнению этапа С6;

- вычисляют количество векторов m₁ в итерации 2k+1;

- если m₁=0, то

- формируют схему для вектора d1 {z, k, t, i};

- формируют схему для d1 {z, k, t, j};

- переходят к выполнению этапа С5;

- формируют схему для вектора d1 {z, k, t, i} из полученных схем для векторов d1 {z=t, 2k, t, i } и d1 {z=t, 1k+1, t, i=t};

- формируют схему для вектора d1{z, k, t, j} из полученных схем

d1[z=t, 2k, t, j} и d1{z=t, 2k+1, t, i=t};

- (С5) вычисляют

t=t+1;

- переходят к выполнению этапа С4;

- (С6) вычисляют

kf(k)=1;

- переходят к выполнению этапа С1;

- (С7) формируют на основе результирующей логической схемы электронную схему для реализации S-блока.

Здесь и далее, в т.ч. в формуле изобретения, отдельные действия, на которые осуществляется переход в ходе реализации предложенного способа, помечены условными обозначениями А1-А6 (действия относятся к этапу анализа) и С1-С7 (действия относятся к этапу синтеза).

Процесс минимизации при реализации S-блоков имеет большое значение, так как при этом уменьшается общее количество элементов, увеличивается надежность, устройства становятся более экономичными. Для минимизации булевых функций был разработан ряд методов, в частности, алгоритмы Квайна-МакКласки, Блейка-Порецкого, в которых булевы функции изображаются в виде дизъюнктивной или конъюктивной нормальной формы и состоят из совокупности логических операций "И", "ИЛИ", "НЕ" [3, 4].

Данные алгоритмы имеют сложность, равную O(n²3ⁿ) при работе по отдельной булевой функции, и О(n²3ⁿ) при работе с системой булевых функций, что требует больших вычислительных ресурсов, поэтому при n>16 многие известные прикладные программы, среди которых, например, программа "Logic Friday" [5], не способны выдать результат.

Существует способ представления булевых функций в виде полиномов Жегалкина над полем характеристики два с соответствующим образом определенными "сложением" ("⊕") и "умножением" ("&") [6].

Для оценки сложности булевых функций в этом случае не требуется их минимизация. Кроме того, по виду полинома Жегалкина можно легко находить количество требуемых для реализации элементарных логических операций. Поэтому применение полиномов Жегалкина, целесообразно использовать для нахождения наименьшего числа логических элементов "⊕" и "&" булевых функций S-блока.

Известно, что каждая булева функция f может быть представлена единственным образом в виде полинома из GF(2ⁿ), степень которого по каждой переменной не превосходит 1 (полином Жегалкина или в алгебраической нормальной форме)

где все 2ⁿ коэффициентов a_i, a_ij,…, а_1…n лежат в поле GF(2) и

x_i∈{0,1}, ∀i=1…n.

Каждый коэффициент а₀, а₁,…, a_ij,…, а_1…n полинома соответствует одному слагаемому.

Представим этот полином через вектор р в котором все 2ⁿ коэффициентов a_i, a_ij,…, a_1…n заменены на коэффициенты a 0 , a 1 , … , a 2 n − 1 соответственно, где a_i∈GF(2),∀i=0…2ⁿ-1.

Пусть функция Nxor(v) определена следующим образом:

где V - произвольный двоичный вектор;

wt_H(v) - вес Хэмминга вектора v.

При анализе булевых функций криптографически значимых S-блоков вполне можно определить, что

1) если M_i - число операций "&" для соответствующего вектора p_i, полученного из i-й булевой функции, то поскольку криптографически значимые S-блоки содержат все или почти все возможные сочетания входных переменных, то М - число операций "&" для всех n векторов p₁, P₂,…, P_n, полученного из i-й булевой функции принимает значение

М=2ⁿ -(n+2)

2) если N p i - число операций "⊕" соответствующего полинома p_i, то значение N p i может быть вычислено по формуле

где Nxor(p_i) определено из выражения (1);

3) из множества полиномов Жегалкина булевых функций S-блока, представленных описанным способом в виде множества векторов Р={p₁,p₂,…p_n}, можно определить количество операций "⊕" для каждой отдельной булевой функции по формуле (2), если реализация S-блока Р={p₁,p₂,…p_n} осуществляется путем независимой реализации составляющих его векторов p₁, p₂,…,p_n, то количество операций "⊕" определяется как

где N_P - количество операций "⊕" с учетом всех исходных коэффициентов многочленов Жегалкина - векторов множества Р,

N_pi - вычислено из выражения (2).

Однако более экономичной является совместная реализация векторов p₁,p₂,…,p_n, составляющих S-блок. Для получения общего количества логических элементов для системы из n булевых функций, т.е. для всего S-блока, необходимо учесть их повторяемость.

Пусть задана t-я пара векторов из коэффициентов полиномов Жегалкина

Тогда, если a_k=b_k для ∀k=0,…,2ⁿ-1, и в полиномах p_i и p_j слагаемые, соответствующие этим коэффициентам, совпадают, то количество общих слагаемых полиномов Жегалкина, соответствующих векторам p_i и p_j (в выражениях (3) и (4)), определяется весом Хэмминга вектора

v = ( p i & p j ) = ( a 0 & b 0 , a 1 & b 1 , … , a 2 n − 1 )

Примем, что вектор v общий для p_i и p_j, имеющий общие компоненты векторов p_i и p_j, равные 1 (т.е. любые коэффициенты a_t=b_t=1). Тогда, пусть СО - количество общих операций "⊕" в паре (p_i,p_j), СО определяется по формуле

CO=Nxor(v),

где v=(p_i&p_j);

Nxor - функция, определенная согласно (1);

N_t - количество операций "⊕" для реализации t-й пары (p_i, p_j) вычисляется по формуле

N_t=Nxor(p_i)+Nxor(p_j)-СО,

а схема реализации S-блока состоит из схем реализации

1) общих элементов пар векторов v;

2) оставшихся элементов векторов p_i (т.е. p_i ⊕ v);

3) оставшихся элементов векторов P_j (т.е. p_j ⊕ v).

Построение (формирование) логической схемы, реализующей соответствующую булеву функцию из вектора p_i, полученного из коэффициентов полинома Жегалкина, является известным процессом (этот процесс описан, например, в [7]) и выполняется с использованием следующих правил:

1) для каждого ненулевого коэффициента a_k∈GF(2), ∀k=0…2ⁿ-1, определяют его позицию k;

2) каждая позиция k ненулевого коэффициента Жегалкина a_k соответствует одному слагаемому из сочетания (по &) входных переменных x₀…x_n-1, для которых в двоичном представлении номера позиции k=0…2ⁿ-1, являются единицами.

Определение общих элементов при совместной реализации множества всех векторов S-блока Р={р₁,р₂,…,p_n} может быть выполнено различными способами. В общем случае требуется полный перебор как по множеству булевых функций (n штук), так и по всем (или почти всем) сочетаниям входных переменных (2ⁿ штук). Очевидно, что при реально требуемых и достаточно больших n такая задача становится трудновыполнимой. Кроме того, после нахождения всех сочетаний повторяющихся элементов, необходимо еще синтезировать логическую схему реализации булевых функций. Как показал опыт, это тоже очень сложная проблема.

Для решения этих проблем, определение общих элементов при совместной реализации множества всех векторов S-блока Р={р₁,р₂,…,p_n}, с учетом автоматизации последующего процесса синтеза логической схемы S-блока, может быть выполнено следующим образом:

1) из множества Р={р₁,р₂,…,p_n} определяют различные пары (p_i,p_j)_t, t=1…n/2 такие, что Nxor(v_t=(p_i&p_j)_t) принимает максимальные значения, где t - номер пары;

2) для каждой пары (p_i, p_j) дополняют изначально пустое множество

D2=D2∪{p_i⊕v_t,p_j⊕v_t};

3) для каждой пары (p_i,p_j)_t дополняют изначально пустое множество

D3=D3∪{v_t};

4) повторяют шаги 1-3 для множества D3 до тех пор, пока количество общих операций "⊕" данного множества станет пустым;

5) повторяют шаги 1-3 для множества D1 до тех пор, пока количество общих операций "⊕" данного множества станет пустым.

Можно отметить, что при каждом повторении этой процедуры исходное множество делится на 2 части. Поэтому, для более наглядного описания процедуры, можно использовать структуру данных двоичного дерева для представления полученных множеств.

Двоичное дерево состоит из вершин и связей между ними, при этом у дерева есть выделенная вершина - корень и у каждой вершины может быть левый и правый наследники (фиг.1).

Будем использовать структуру данных полного двоичного дерева для представления результатов выполнения рассмотренной процедуры следующим образом.

Можно установить следующие правила построения двоичного дерева:

1) вершина дерева - исходное множество Р, состоящее из n векторов, из которого составлено множество из n/2 пар, перенумерованное с учетом максимального значения Nxor(v_t=(p_i,&p_j)_t)(на шаге 1);

2) левый наследник этой вершины - множество D2;

3) правый наследник этой вершины - множество D3;

4) вершина не имеет наследников, если число векторов в ней равно 1 или число общих элементов во всех парах равно 0 (данная вершина называется листом).

Будем нумеровать каждую вершину дерева по принципу: "сверху вниз" и "слева направо". Тогда:

- k-я вершина имеет наследников 2k-го и (2k+1)-го (фиг.1),

- если в k-й вершине имеется q элементов (q/2 пар), то ее правый наследник имеет q/2 элементов (q/4 пар), а левый наследник имеет тоже q элементов (q/2 пар).

Будем обозначать каждый вектор в паре (p_i, p_j) в вершине k для получения множества D1 путем сопоставления

d1{z,k,t,i}=p_i,

d1{z,k,t,j}=p_j,

где k - номер вершины вектора P_i,

t - номер пары, которая имеет часть p_i (значение t=0 означает, что для вектора p_i еще не найдена пара),

z - номер пары родителей (это пара в вершине k/2; если k=1 - это корень дерева, и тогда z=0);

i, j - номер вектора во множества Р.

Тогда

- общие элементы v=(p_i, p_j) для конкретной пары будут обозначаться как v{k,t}=(d1{z,k,t,i}&d1{z,k,t,j}), причем v{k,t} становится элементом d3{z=t,2k+1,t,i=t} в D3, а значение t для данного вектора будет определяться при применении процедуры для множества D3,

- оставшиеся компоненты d1{z,k,t,i}⊕v{k,t} и d1[z,k,t,j}⊕v {k,t} становятся элементами d2{z=t,2k,t,i} и d2{z=t,2k,t,j} в D2, а значения t данных векторов будут определяться при применении процедуры для множества D2.

Пример. Для конкретного S-блока {6, 12, 5, 3, 2, 14, 0, 10, 9, 13, 8, 11, 4, 1, 7, 15} после применения описанной процедуры результаты можно представить в виде дерева (фиг.2), в котором

- в вершине 1 есть пары (d{0,1,1,2},d{0,1,1,4}), {d{0,1,2,1}, d{0,1,2,3});

- в вершине 3 есть пара (d{1,3,1,1},d{2,3,1,2}), и в том числе вектор v{3,1}=0.

Для синтеза схемы, на основе полученных результатов (оставшихся и общих компонентов) после применения алгоритма определения общих элементов, на основе построенного дерева, последовательно выполняются действия в направлениях "снизу вверх" и "справа налево" следующим образом.

Для каждой t-й пары в k-й вершине (с учетом указанных выше правил)

1) сначала получают логическую схему для общих компонентов d1{t,2k+1,t,t} правого наследника (схема обозначается как СХР {t, 2k+1,t,t});

2) получают логическую схему СХР {t,2k,t,i} для вектора d1{t,2k,t,i} левого наследника;

3) получают логическую схему СХР {t,2k,t,j } для вектора d1{t,2k,t,j};

4) выполняют синтез схемы СХР [z,k,t,i} для вектора d1{z,k,t,i} из синтезированных схем векторов d1{t,2k,t,i} и d1{t,2k+1,t,t} на основе соотношения

5) выполняют синтез схемы CXP[z,k,t,j} для вектора d1{z,k,t,j} на основе синтезированных схем векторов d1{t,2k,t,j} и d1{t,2k+1,t,t} согласно соотношению

6) сохраняют схемы СХР {z,k,t,i}, СХР {z,k,t,j} реализации функций d1{t,2k,t,i}, d1{z,k,t,j} для t-й пары в k-й вершине.

Таким образом, схема СХР {z,k,t,i} реализации каждой функции p_i t-й пары в k-й вершине состоит из синтезированной схемы СХР {z=t,2k+1,t,i=t} в правом наследнике и синтезированной схемы СХР {z=t,2k,t,i} в левом наследнике.

Другими словами, для построения логической схемы, обход дерева в последовательности "правый-левый-корень" применяется следующим образом:

1) обходят правое поддерево;

2) обходят левое поддерево;

3) обрабатывают корень.

Соответственно, из корня дерева (k=1) выполняют:

1) обход для правого поддерева вершины k (т.е. обход поддерева, имеющего корень 2k+1);

2) обход для левого поддерева вершины k (т.е. обход поддерева, имеющего корень 2k);

3) обработку корня k (применяют процедуру обработки в k-й вершине).

При обработке корня k либо формируют схемы для векторов в этой вершине, если она является листом, либо синтезируют схемы для векторов в этой вершине из синтезированных подсхем в ее наследниках 2k+1 и 2k с использованием преобразований (5) или (6), если вершина k не является листом.

При применении этой процедуры для синтеза схемы сначала будет обрабатываться "самая правая" вершина построенного дерева, затем левая, и, наконец, корень дерева (вершина с k=1).

Блок-схема процесса формирования S-блока с минимальным количеством логических элементов представлена на фиг.3 (отдельные блоки пронумерованы цифрами от 1 до 5) и описывает следующие действия.

Блок №1 - задают исходный S-блок (табл.1)

Блок №2 - формируют систему булевых функций в виде таблиц истинности.

Значения x и соответственные S(x) записаны в двоичном виде из n бит, т.е. х=х₁х₂…x_n и S(x)=s₁s₂…s_n, где x_i∈{0,1} и s_i=S_i(x)∈{0,1},∀i∈[1,n]. Затем значения представляются в виде таблицы истинности из 2ⁿ значений булевых функций S_i, упорядоченных в лексикографическом порядке по входным переменным следующим образом (табл.2)

В этой таблице, каждый столбец S_i(m), состоящий из 2ⁿ значений, представляется в следующем виде:

Блок №3 - осуществляют умножение матрицы L_n на значения булевой функции и получают вектор коэффициентов полинома Жегалкина. Аналогичным образом получают остальные векторы коэффициентов полиномов Жегалкина

Р={р₁,р₂,…,p_n}.

Для этого строят матрицу L_n размера 2ⁿ×2ⁿ следующим рекуррентным образом (известная матрица Адамара):

где ⊕ - знак тензорного произведения матриц;

Затем для каждого i=1…n находят коэффициенты полинома Жегалкина:

P_i=L_nS_i

и формируют полученный вектор p_i, компоненты которого составлены из соответствующих коэффициентов a 0 , a 1 , … , a 2 n − 1 .

Блок №4 - определяют общие логические элементы реализации S-блока (детальная блок-схема этого процесса представлена на фиг.4).

Для удобства описания в детальной блок-схеме блока №4 отдельные действия или последовательности действий пронумерованы в виде подблоков №№4.1 - 4.16.

В подблоке №4.1 выполняется следующие действия:

- вычисляют для каждого из полученных векторов p_i величину

Nxor(p_i);

- вычисляют общее количество операций "⊕" N_P для построения S-блока без процедуры минимизации

,

- устанавливают начальное значение

k=1,

- формируют множество D1{z,k,t,i} векторов длины 2ⁿ (исходно пустое), где каждому вектору дополнительно сопоставлены значения

z=0, t=0;

- добавляют во множество D1 векторы

d1{z=0,k=k,t=0,i}=p_i;

- устанавливают начальное значение

kt=0.

В подблоках №4.2-4.16 находят наиболее часто встречающиеся подпоследовательности компонент в векторах p_i, выполняя следующие действия:

- (А1) формируют исходно пустое множество DTMP[z,k,t=0,i} векторов длины n, где каждому вектору дополнительно сопоставлены значения t=0 и k=k;

- формируют исходно пустое множество D2{z,2k,t,i} векторов длины 2ⁿ;

- формируют исходно пустое множество D3{z,2k+1,t,i} векторов длины 2ⁿ;

- устанавливают начальное значение для номера пары

t=1

- (А2) (подблок №4.4), если выполняется соотношение

|D1{z,k,t=0,i}|<2,

то переходят к выполнению этапа A3 (к подблоку №4.9);

- (подблок №4.5) определяют пару векторов (d1{z,k,t,i}, d1{z,k,t,j}) во множестве D1{k}, причем i≠j такую, что величина

принимает максимальное значение;

- (подблок №4.6) в случае если Nxor_A (v{k,t})=0 и определенная пара является первой (t=1), т.е. нет общих элементов между векторами множества D\{k}, то переходят к выполнению этапа А5 (к подблоку №4.15);

- (подблок №4.7) добавляют во множество DTMP последовательно векторы (d1{z,k,t,i}, d1{z,k,t,j}) для определенной пары t

- прибавляют к величине СО число общих сумматоров для данной пары

CO=CO+Nxor_A

- добавляют во множество D3 вектор

- удаляют из векторов каждой пары общие элементы

- добавляют во множество D2 оба вектора

- (подблок №4.8) удаляют участвовавшие пары векторов из множества D1

- вычисляют

t=t+1

- вычисляют мощность множества векторов D1

|D1{z,k,t=0,i}|

- переходят к выполнению этапа А2;

- (A3) (подблок №4.9) временно сохраняют множества DTMP векторов (d1{z,k,t,i}, d1{z,k,t,j}) и множества векторов D2{z,2k,t,i} и D3{z,2k+1,t,i};

- (подблок №4.10) вычисляют

kp=2k,

kv=2k+1;

- (подблок №4.11) если выполняется соотношение

|D3{z,k=kv,t,i}|<2,

то переходят к выполнению этапа А4;

- вычисляют

k=kv

- (подблок №4.14) присваивают элементам множества D1{k} значения элементов множества D3{kv}

d1{z,k,t,i}=d3{z,kv,t,i}

- вычисляют

kt=0

- переходят к выполнению этапа А 1;

- (А4) (подблок №4.12) если выполняется соотношение

|D2{z,k=kp,t,i}|<2,

то переходят к выполнению этапа А6;

- (подблок №4.13) вычисляют

k=kp,

kt=1

- присваивают элементам множества D1{z,k,t,i} значения элементов множества D2{z,kp,t,i}

d1{z,k,t,i}=d2{z,kp,t,i}

- переходят к выполнению этапа А1;

- (А5) (подблок №4.15) если kt=1, то переходят к выполнению этапа А6 (блока №5 на фиг.3), иначе переходят к выполнению этапа А4;

- вычисляют количество сумматоров при совместной реализации векторов S-блока

N=N_p-CO

Блок №5 - получают результирующую логическую функцию, выполняя следующие действия (блок-схема данного процесса представлена на фиг.5, 6):

- (подблок №5.1) вычисляют

k=1

- формируют вспомогательный вектор kf(k), изначально имеющий нулевые элементы;

- (С1) если kf(k)=1 (значение вектора kf{k)=1 означает, что схемы векторов в вершине k уже синтезированы), то переходят к выполнению этапа С2;

- вычисляют

k=2k+1

(чтобы затем перейти к правому наследнику вершины k);

- вычисляют количество векторов m в итерации k;

- если m≠0, то переходят к выполнению этапа С1;

- вычисляют

k={k-1)/2

(т.е. возвращаются к родителю вершины k, являющейся листом);

- переходят к выполнению этапа С3;

- (С2) если k является четным, то вычисляют

k=k/2

- переходят к выполнению этапа С3;

- вычисляют

k=k-1

- если k=0, то переходят к выполнению этапа С7, иначе - переходят к выполнению этапа С1;

- (С3) (блок-схема этого этапа представлена на фиг.6) вычисляют количество векторов m в итерации k;

- если m-1, то

- формируют схему для вектора d1{z,k,t,i};

- переходят к выполнению этапа С6;

- вычисляют

t=1

- (С4) если t>m/2, то переходят к выполнению пункта С6;

- вычисляют количество векторов m₁ в итерации 2k+1;

- если m₁=0, то

- формируют схему для вектора d1{z,k,t,i};

- формируют схему для d1{z,k,t,j};

- переходят к выполнению этапа С5;

- формируют схему для вектора d1{z,k,t,i} из полученных схем для векторов d1{z=t,2k,t,i} и d1{z=t,2k+1,t,i=t};

- формируют схему для вектора d1{z,k,t,j} из полученных схем d1{z=t,2k,t,j} и d1{z=t,1k+1,t,i=t}.

- (C5) вычисляют

t=t+1

- переходят к выполнению этапа С4;

- (С6) вычисляют

kf(k)=1

- переходят к выполнению этапа С1;

- (С7) формируют на основе результирующей логической схемы электронную схему для реализации S-блока.

По определенной выше результирующей логической схеме (фиг.7) система полиномов, соответствующих булевым функциям заданного S-блока, может быть аппаратно реализована на различной основе (на интегральных микросхемах малой и средней степени интеграции, а также ПЛИС), при этом аппаратная реализация будет содержать минимальное количество логических элементов.

Краткое описание чертежей

На фиг.1 показан пример двоичного дерева.

На фиг.2 показано двоичное дерево, полученное на этапе анализа для конкретного примера.

На фиг.3 показана общая блок-схема алгоритма формирования S-блока с минимальным количеством логических элементов.

На фиг.4 показана общая блок-схема алгоритма для этапа анализа (блока №4) в алгоритме формирования S-блока с минимальным количеством логических элементов.

На фиг.5 и фиг.6 показана общая блок-схема алгоритма для этапа синтеза (блока №5) в алгоритме формирования S-блока с минимальным количеством логических элементов.

На фиг.7 показан процесс этапа синтеза логической схемы реализации булевых функций заданного S-блока для конкретного примера.

На фиг.8 показана синтезированная логическая схема реализации булевых функций заданного S-блока для конкретного примера.

Осуществление изобретения

Рассмотрим пример реализации предложенного способа для S-блока на 4 бита, имеющего вид

S₁={6,12,5,3,2,14,0,10,9,13,8,11,4,1,7,15}

Система булевых функций S-блока формируется в виде таблицы истинности (фиг.1, блок №2).

Затем, путем умножения матрицы L_n размером 2ⁿ×2ⁿ (матрица L_n представлена в выражении (7)) для каждой булевой функции вычисляют коэффициенты многочлена Жегалкина, записанные в виде векторов р₁,р₂,…,p_n (фиг.3, блок №3, первые два числа указывают количество операций умножения "&" и операций сложения "⊕" соответственно)

По коэффициентам многочлена Жегалкина можно определить число входов для логических элементов "&" и количество элементов "⊕" для каждой отдельной булевой функции.

Для получения общего количества логических элементов для системы из n булевых функций, т.е. для всего S-блока, необходимо учесть их повторяемость (фиг.3, блок №4). Сначала выпишем в порядке возрастания все сочетания входных переменных, встречающиеся хотя бы один раз, и запишем в виде "результирующего полинома" - столбец 3 (табл.3). "Результирующий полином" показывает, какие сочетания входных переменных участвуют в построении S-блока, а какие - нет. Из полученного выражения получим результат - столбец 4.

- количество необходимых операций "&" равно 10;

- количество слагаемых с количеством входов, равным 1, равно 4;

- количество операций "&" с количеством входов, равным 2, равно 6;

- количество операций "&" с количеством входов, равным 3, равно 4;

- количество операций "&" с количеством входов, равным 4, равно 0;

- общее количество число необходимых операций "⊕" равно 14;

- минимальное количество операций "⊕", равное 2ⁿ-2, определенное числом единиц "результирующего полинома"? при этом сумма количества операций "⊕" отдельно по всем выходам N_p=28.

Однако знание общего количества необходимых операций "&" и "⊕", не позволяет построить конкретную схему, реализующую данный S-блок, на этих логических элементах. Для построения конкретной схемы воспользуемся каждым набором коэффициентов Жегалкина отдельно, для каждой булевой функции.

Для заданного S-блока S₁ после применения этого алгоритма получены следующие результаты:

Сначала для формирования S-блока с минимальным количеством логических элементов (блок №4 на фиг.3 или блок-схема на фиг.4) проводят этап анализа.

Пары в вершине k=1, число пар t=2 (см фиг.2):

- пара 1 (t=1)=(2, 4), число общих операций "⊕" равно 4:

- пара 2 (t=2)=(1,3), операций "⊕"=1:

В вершине k=3, число пар t=1, число общих операций "⊕" равно 0:

Пары в вершине k=2, число пар t=2:

- пара 1 (t=1)=(2,3), число общих операций "⊕" равно 1:

- пара 2 (t=2)=(1,4), число общих операций "⊕" равно 0:

В вершине k=5, число пар t=1, число общих операций "⊕" равно 0:

Пары в вершине k=4, число пар t=1:

- пара 1 (t=1)=(1,2), число общих операций "⊕" равно 1:

- пара 2 (t=2)=(3,4), число общих операций "⊕" равно 0:

В вершине k=9, число пар t=1, число общих операций "⊕" равно 0:

Число общих элементов в вершине k=8 равно 0, число векторов равно 4:

- пара 1 (t=1)=(3,4), число общих операций "⊕" равно 0:

- число общих операций "⊕" СО=7;

- сумма операций "⊕" N=N_P - СО=21;

- дерево, построенное при анализе, представлено на фиг 2.

Затем проводят этап синтеза логической схемы с минимальным количеством логических элементов (этап синтеза представлен блоком №5 на фиг.3 или блок-схемами на фиг.5 и фиг.6).

Таким образом, получают результирующую схему СХР{0,1,2,1} для р₁, СХР{0,1,1,2} для р₂, СХР{0,1,2,3} для р₃р₃, СХР{0,1,1,4} для Р₄.

Определенная схема аппаратной реализации S₁ представлена на фиг.8.

Для оценки эффективности предложенного способа была также составлена программа для ЭВМ, в которой реализованы все действия способа. Формирование такой программы доступно любому профильному специалисту по программированию (программисту) на основе описанных выше действий в способе и может быть выполнено на каком-либо универсальном языке программирования (например, на языке С).

В известных способах [3, 4] вычислительная сложность алгоритмов Квайна-МакКласки, Блейка-Порецкого определяется выражением

T(n)=O(n²3ⁿ)

при работе по отдельной булевой функции, и

T(n)=O(n²3²ⁿ)

при работе с системой булевых функций.

Вычислительная сложность предлагаемого способа применения многочленов Жегалкина для минимизации булевых функций S-блока при реализации в форме алгоритма составляет

T(n)=O(n(n-1)2^n-1),

что, очевидно, меньше.

Сравнение результатов минимизации проводилось для программы, реализующей предложенный способ? и для известной программы "Logic Friday" [5], на одном компьютере, последовательно, при одинаковых исходных данных.

В качестве исходных данных задавались S-блоки (размерностью 8 и 16 бит, табл.4).

Можно отметить, что предлагаемый способ позволяет

- уменьшить общее число операций "&" и "⊕" для результирующей логической функции;

- обеспечить получение результата для S-блоков больших размерностей, в отличие от известной программы.

Таким образом, предлагаемый способ уменьшает схемотехнические затраты - количество операций сложения и умножения при реализации заданного S-блока.

Последующая схемотехническая реализация полученного S-блока может быть осуществлена известными методами, предпочтительной формой для использования в современной компьютерной технике является реализация на ПЛИС, но это н