Фазовая модуляция и минимизация шума при одновременных вибросейсмических исследованиях

Фазовая модуляция и минимизация шума при одновременных вибросейсмических исследованиях

Иллюстрации

Показать все

Реферат

Предпосылки

При сейсмической разведке с использованием способов с одновременно работающими вибраторами группу источников сейсмической энергии (например, вибраторов) используют для излучения сейсмических сигналов в геологическую среду. Часть этих сигналов отражается от границ раздела между подземными пластами и/или отражается в пластах обратно к земной поверхности, где их обнаруживают на одном или нескольких приемниках. Время, затрачиваемое на прохождение сигнала от конкретного вибратора к конкретному приемнику, дает показатель длины пути пробега сигнала между этим вибратором и этим приемником, на основании которого можно вывести заключение о структуре геологических пластов.

При использовании вибросейсмических способов с одновременно работающими вибраторами энергия передается в геологическую среду от совместно и одновременно работающих вибраторов с многочисленных мест расположения источников. Поэтому на каждом приемнике обнаруживают преломленную и отраженную энергию, которая излучалась всей группой вибраторов (Кстати сказать, одновременное свипирование влечет за собой перекрытие свип-сигналов. Свип-сигналы могут или могут не начинаться и/или заканчиваться в один и тот же момент времени, при условии, что имеется некоторый участок перекрытия свип-сигналов). Затем данные, зарегистрированные на каждом приемнике, должны быть обработаны с тем, чтобы можно было выделить сигнал, соответствующий каждому отдельному вибратору.

Это выделение можно получать при образовании каждым вибратором многочисленных свип-сигналов или выполнении многочисленных ударных воздействий, когда относительная фаза сигналов, излучаемых вибраторами, изменяется от вибратора к вибратору и от ударного воздействия к ударному воздействию (хотя относительную фазу удерживают постоянной на протяжении длительности соответствующих свип-сигналов). Это можно показать на примере случая двух вибраторов, дважды работающих одновременно. Если они работают в фазе относительно друг друга при первом свип-сигнале, но со сдвигом фаз на 180° в течение длительности второго свип-сигнала, на приемнике будут регистрироваться два сигнала (то есть относительный фазовый угол между сигналами возбуждения двух вибраторов составляет 180° в течение длительности второго свип-сигнала) (Кстати сказать, сигналом возбуждения или сигналом управления можно возбуждать все четыре свип-сигнала с одной и той же амплитудой относительно качающейся частоты, возможно, с коническими краями, поскольку амплитуда должна быть линейно возрастающей в начале и линейно спадающей в конце. Управляющий сигнал может начинаться на низкой частоте и заканчиваться на высокой частоте, а частота может повышаться линейно в зависимости от времени). Результирующие зарегистрированные сигналы можно складывать друг с другом, чтобы определять сигнал, поступающий от первого вибратора, или вычитать, чтобы определять сигнал, поступающий со второго вибратора.

Хотя на протяжении ряда лет разделение сигналов улучшается, тем не менее минимизацию шума и разделение сигналов можно совершенствовать для лучшего определения местоположения представляющих интерес подземных областей.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Признаки и преимущества вариантов осуществления настоящего изобретения станут понятными из прилагаемой формулы изобретения, нижеследующего подробного описания одного или нескольких примеров вариантов осуществления и соответствующих чертежей, на которых:

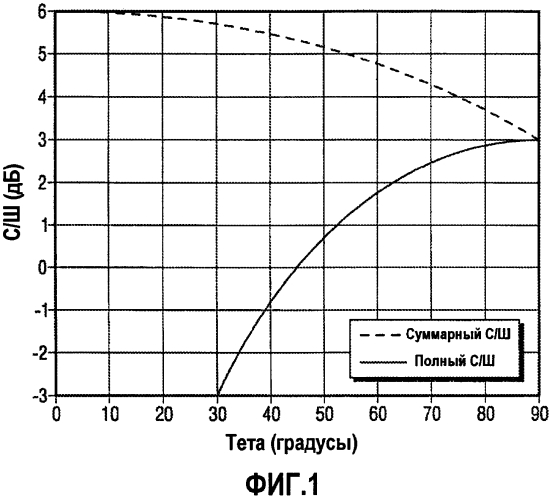
фиг. 1 - график отношений суммарного и полного сигналов к шуму (С/Ш) для случая матриц источников размером 2×2 в зависимости от фазы;

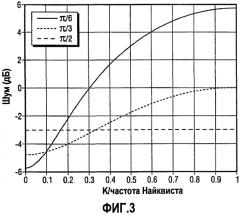
фиг. 2 - график максимального и минимального шумов как функция фазы для случая матриц 2×2;

фиг. 3 - график спектра шума для трех значений фазы в матрицах 2×2;

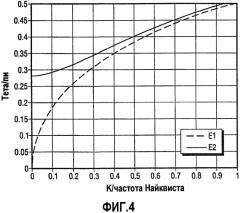
фиг. 4 - график оптимальной фазы в зависимости от граничной частоты для целевых функций;

фиг. 5 - график фаз матрицы в зависимости от граничной частоты для целевых функций;

фиг. 6 - график пространственного спектра шума для различных наборов оптимальных углов (матрицы 3×3) при целевой функции Е2;

фиг. 7 - график пространственного спектра шума для различных наборов оптимальных углов (матрицы 3×3) при целевой функции Е1; и

фиг. 8 - структурная схема системы для выполнения различных вариантов осуществления изобретения.

ПОДРОБНОЕ ОПИСАНИЕ

В нижеследующем описании изложены многочисленные конкретные подробности, но варианты осуществления изобретения могут быть применены на практике без этих конкретных подробностей. Хорошо известные схемы, структуры и способы показаны детально для исключения затруднения понимания этого описания. «Вариант осуществления», «различные варианты осуществления» и т.п. означают, что вариант (варианты) осуществления, характеризуемый таким образом, может включать в себя конкретные признаки, структуры или характеристики, но не каждый вариант осуществления обязательно включает в себя конкретные признаки, структуры или характеристики. Несколько вариантов осуществления могут иметь некоторые или все признаки, описанные для других вариантов осуществления, или могут совсем не иметь их. «Первый», «второй», «третий» и т.п. характеризуют общий объект и обозначают различные примеры аналогичных объектов. Такие определения не означают, что объекты, охарактеризованные таким образом, должны находиться в заданной пространственной, временной, ранговой или любой другой последовательности. «Соединенный» может указывать на элементы, находящиеся в непосредственном физическом или электрическом контакте друг с другом, а «связанный» может указывать на элементы, действующие совместно или взаимодействующие друг с другом, но они могут быть или могут не быть в непосредственном физическом или электрическом контакте. Кроме того, хотя аналогичные или одинаковые позиции могут использоваться для обозначения одинаковых или аналогичных деталей на различных фигурах, такой подход не означает, что все фигуры, включающие в себя аналогичные или одинаковые позиции, являются составной частью единственного или одного и того же варианта осуществления.

Как упоминалось выше, при обычных вибросейсмических исследованиях с одновременно работающими вибраторами относительные фазовые углы между сигналами управления различных вибраторов удерживают постоянными в течение длительности свип-сигнала. Однако вариант осуществления изобретения включает в себя одновременные сигналы возбуждения, относительный сдвиг (сдвиги) фазовых углов которых изменяется на протяжении части (или длительности) одновременных свип-сигналов.

Например, при обычных вибросейсмических исследованиях с одновременно работающими вибраторами многочисленные вибраторы свипируют на протяжении диапазона частот при использовании управляющего механизма, который стремится поддерживать постоянную относительную фазу между различными вибраторами. Рассмотрим два вибратора V1 и V2 с контроллерами, которые пытаются поддерживать толкающие усилия F1 и F2 опорной плиты вибратора. Преобразованиями Фурье двух толкающих усилий являются f1 и f2. Согласно обычным способам отношение f1 к f2 является постоянным в зависимости от частоты (Кстати сказать, наряду с тем, что управляемой величиной необязательно является толкающее усилие, отношение параметров управления является постоянным в зависимости от частоты.) Однако в варианте осуществления относительная фаза (то есть сдвиг фаз) параметров управления многочисленных вибраторов регулируется так, что изменяется в зависимости от частоты. Например, два вибратора возбуждаются с фазами, параметры управления которых (например, толкающее усилие) следуют по расчетной траектории

при этом вибратор 1 следует по траектории F_A при первом ударном воздействии и по F_B при втором ударном воздействии, а вибратор 2 следует по траектории F_B при первом ударном воздействии и по траектории F_A при втором ударном воздействии, где φ - скорость изменения частоты, f₀ - начальная частота, W - гладкая функция (которая возрастает от 0 до максимума в течение короткого периода времени, остается максимальной в течение отрезка времени и затем снижается до 0 в течение короткого периода времени) и Θ - сдвиг фазового угла. Согласно обычным способам Θ является постоянным, но в варианте осуществления изобретения Θ изменяется как функция времени. В одном варианте осуществления Θ(t) близок к 0 в начале свип-сигнала, возрастает до π/2 в середине свип-сигнала и остается на уровне π/2 до конца свип-сигнала. Таким образом, относительный фазовый угол Θ (t) параметра управления свип-сигнала (например, сигналов управления или возбуждения) изменяется на протяжении всего или части хода двух или большего количества одновременных свип-сигналов. Не требуется, чтобы свип-сигналы обязательно начинались и/или заканчивались в одно и тоже время, но в варианте осуществления они являются одновременными (то есть перекрывающимися).

Хотя в примере, приведенном выше, имеются два вибратора, образующих свип-сигнал с разверткой вверх (с частотой, возрастающей со временем) при постоянной скорости изменения частоты, варианты осуществления можно применять для любого числа вибраторов с переменной скоростью изменения частоты и для свип-сигналов с разверткой вверх или свип-сигналов с разверткой вниз (с частотой, уменьшающейся со временем). Кроме того, хотя в приведенных выше примерах вибраторы находятся на суше, а сигналы принимаются геофонами, вибраторы можно располагать в других окружающих средах, например на морском дне, или подвешивать в воде. Отраженные или преломленные волны вибратора можно принимать другими средствами, такими как, например, акселерометры или гидрофоны. Кроме того, одновременное свипирование можно выполнять при использовании изменяющихся свип-сигналов, например, в методике исследований с перекрывающимися свип-сигналами, высокоточных вибросейсмических методиках и т.п.

В следующих параграфах различные варианты осуществления изобретения изложены более подробно.

Влияние фазы и фазовой модуляции

При вибросейсмических исследованиях с одновременно работающими вибраторами несколько вибраторов (N) могут свипировать несколько раз (М) при закреплении на местах. Свип-сигналы могут быть идентичными (по меньшей мере в соответствии с конструкцией) во всех отношениях за исключением одного, а именно начальной фазы вибратора. В частотной области зависимость между сигналом, измеряемым на приемнике, и передаточными функциями из отдельных точек расположения вибраторов (ТРВ) может быть описана в виде матричного уравнения G=SI, где G представляет сигналы приемников (вектор M×1 для каждого приемника), S представляет матрицу (M×N) и I представляет вектор (N×1) индивидуальных импульсных характеристик. Поскольку все свип-сигналы имеют одинаковые амплитуды, но различные фазы, все элементы S можно нормировать, чтобы иметь амплитуду 1, и поэтому они характеризуются только фазой. В других вариантах осуществления не требуется, чтобы амплитуды были одинаковыми.

Некоторые стратегические решения в вибросейсмическом способе с одновременно работающими вибраторами так или иначе связаны с наилучшим выбором фаз. Критерии для принятия решения относительно используемых фаз могут быть основаны на влияниях инверсии матрицы на шум (например, шум окружающей среды или когерентный шум, который является следствием гармоник вибраторов).

При рассмотрении взятых отдельно влияний шума окружающей среды и в предположении, что шум, начиная от одного ударного воздействия и кончая следующим, является некоррелированным, минимизация полного шума в оцениваемой импульсной характеристике из каждой точки расположения вибратора, рассматриваемой отдельно, эквивалентна выбору матрицы S, все собственные значения которой представляют собой равные амплитуды. Однако, если вместо рассмотрения полного шума отдельно в каждой точке расположения вибратора, рассматривать шум после применения дополнительной фильтрации (например, после усреднения данных по нескольких точкам расположения вибраторов, применения пространственной фильтрации нижних частот и т.д.), то другие фазы могут быть оптимальными, и может быть предпочтительно иметь матрицу фаз, которая изменяется в зависимости от частоты (то есть, относительные фазы различных вибраторов зависят от частоты). Кроме того, при оптимизации можно учитывать гармонические помехи от следующего ударного воздействия во время одновременного возбуждения волн.

То есть может быть предпочтительно изменять относительную фазу между свип-сигналами во время исследований с одновременно работающими вибраторами, даже если записи из отдельных точек расположения вибраторов последовательно суммируют для образования одной группы. Улучшение данных, возможное в результате улучшения статических свойств точек ударного воздействия и коррекции вариаций сигнатур источников, может уравновешивать любое снижение отношения сигнала к шуму (С/Ш) с учетом случайного шума окружающей среды.

Кроме того, использование оптимизации фаз вибраторов (то есть изменяющегося относительного фазового угла) в сочетании со связанными одновременными возбуждениями волн может приводить к улучшению пространственной дискретизации, коррекции статических свойств отдельных точек ударных воздействий и сигнатур и улучшению качества данных в целом в пределах одного и того же периода времени для каждой точки расположения вибраторов, как при обычном групповом возбуждении волн.

Фаза и уровни отношения сигнала к шуму

Хотя нижеследующее можно распространить на аналитический анализ для любого размера матрицы S, в пояснительных целях нижеследующий пример касается матрицы S источника размером 2×2 (два вибратора, возбуждение волн два раза), записываемой в следующем виде:

В варианте осуществления для каждого вибратора и каждого ударного воздействия образуемый фактический свип-сигнал является действительной частью соответствующего элемента матрицы S, умноженной на свип-сигнал с такой же полосой частот. Поэтому, если первое ударное воздействие от первого вибратора имеет форму, определяемую как F_A в уравнении 1, то первое ударное воздействие для второго вибратора может быть

и второе ударное воздействие для первого вибратора может быть:

Фазу каждой строки можно поворачивать независимо (Это включает в себя предположение о том, что вибраторы совершают ударные воздействия индивидуально и неоднократно. Нет надобности в том, чтобы два вибратора были одинаковыми на 100%). Обращение этой матрицы дает

Если имеется шум n₁ при первом ударном воздействии и шум n₂ при втором ударном воздействии, то шум (g₁ и g₂) t который появляется в отдельных сигналах, будет соответственно

В предположении, что шум в каждой записи является независимым и имеет одно и то же ожидаемое значение, суммарная мощность шума имеет вид

Однако, если две записи сначала суммируют, шум имеет вид

Таким образом, как видно на фиг. 1, при значениях Θ меньше чем π/2 (90°) наименьшее значение суммарной мощности получается при Θ=0, при этом отсутствует влияние на полную мощность. Поэтому без утраты общности можно построить график зависимости шума от угла Θ. На фиг. 1 показаны отношение суммарного сигнала к шуму и отношение полного сигнала к шуму, связанные с уровнем отношения сигнала к шуму, который получается при возбуждении волн одним вибратором в первой точке расположения вибратора и затем возбуждении волн одним вибратором во второй точке расположения вибратора при использовании одинаковых свип-сигналов.

Как показано на фиг. 1, выбор угла, который является наилучшим для полного шума, может быть менее оптимальным для суммарного шума. По мере уменьшения Θ от 90 до 0° отношение суммарного сигнала к шуму повышается на 3 дБ, приближаясь к уровню, ожидаемому при групповом ударном воздействии (то есть когда два вибратора дважды возбуждают волны, находящиеся в фазе). Влияние изменения угла на полный шум является более сильным, поскольку вместо приближения к конечному значению отношение сигнала к шуму падает до минус бесконечности, когда матрица становится сингулярной.

Если для различных частот имеется различие в относительной важности отношения суммарного сигнала к шуму в зависимости от отношения полного сигнала к шуму, то в варианте осуществления может быть предпочтительно изменять угол Θ в зависимости от частоты. В общем случае, если два вибратора находятся физически близко друг к другу, на нижнем конце частотного диапазона отношение суммарного сигнала к шуму может быть более важным, тогда как на верхнем конце частотного диапазона отношение полного сигнала к шуму может быть более важным.

Пространственная фильтрация шума

Результаты из фиг. 1 не зависят от пространственного распределения вибраторов и показанные вклады различных вибраторов можно анализировать индивидуально, а коррекции можно выполнять до образования групповой суммы без серьезного влияния на подавление случайного шума.

Одно применение одновременного возбуждения волн означает повышение пространственной плотности выборки ударных воздействий и, следовательно, вклады от отдельных вибраторов нельзя просто складывать друг с другом для образования группы. Точнее, пространственную фильтрацию некоторого вида можно применять к области общей точки приема.

Точно так же, когда различные матрицы источников приводят к различным отношениям суммарного и полного сигналов к шуму, различные матрицы источников также приводят к различным пространственным спектрам шума, когда отдельные вибраторы имеют известное пространственное распределение. Например, рассмотрим ситуацию, в которой вибраторы возбуждают волны вдоль линии при фиксированном пространственном разнесении вибраторов. При использовании матрицы S размером 2×2, параметризованной так, как указано выше, шум каждой трассы имеет вид

Рассмотрение шума (по пространству) как некоррелированной скалярной величины и предположение, что точки расположения вибраторов разнесены на расстояния d, с учетом выполнения пространственного преобразования Фурье, приводят к и поэтому пространственный спектр мощности равен

На фиг. 2 показан шум в децибелах как функция Θ, нормированный относительно полного шума, для (φ-kd)=2nπ и (φ-kd)=(2n+1)π (Кривая, которая приближается к -6 дБ по оси y справа, является первой, а кривая, которая приближается к -6 дБ слева является второй). Когда Θ=π/2, матрица источника имеет вид и шум не зависит от пространственной частоты. При других значениях Θ имеются волновое число, при котором шум является минимальным, и волновое число, при котором шум является максимальным. По мере отклонения Θ от π/2 разность между максимальным и минимальным значениями возрастает.

Одна ситуация, в которой желательно повышать отношение сигнала к шуму при небольших пространственных волновых числах, существует, когда основные отражающиеся сигналы могут располагаться в пространственно-частотной области. Высокие пространственные волновые числа можно отфильтровать (например, на низких частотах) во время обработки, так что если случайный шум присутствует на этих пространственных частотах, шум можно удалять позднее в обрабатывающей цепочке.

В предположении отсутствия предпочтительного направления (вследствие чего является желательной симметричная относительно 0 кривая шума в зависимости от пространственного волнового числа при k=0) φ можно приравнять κ нулю.

На фиг. 3 показан шум как функция пространственной частоты для трех значений Θ (π/6, π/3 и π/2). При наибольшем угле шум не зависит от пространственной частоты, и уровень шума составляет -3 дБ при возбуждении волн отдельным вибратором. При среднем угле первоначальный уровень шума повышается (при том же пространственном волновом числе Найквиста) и составляет -4,75 дБ при нулевом волновом числе, а при наименьшем угле шум при нулевом волновом числе снижается до -5,7 дБ при нулевом волновом числе (что близко к минимально возможному -6), но повышается в соответствии с аналогичной величиной Найквиста.

Если обрабатывающая цепочка, через которую проходят регистрируемые данные, включает в себя частотно-зависимую пространственную фильтрацию (например, частотно-волновочисленную фильтрацию), то может быть предпочтительно, чтобы относительный фазовый угол Θ был небольшим на низких частотах и при этом возрастал до π/2 на частоте, на которой заканчивается полная ширина полосы пространственных частот.

Этот пример исключительно для ясности описания приведен для 2 вибраторов, а пространственные частоты рассматриваются только в одном направлении. В случае более чем двух вибраторов может быть предпочтительно, чтобы относительный фазовый угол между вибраторами был меньше на низких частотах, чем на высоких частотах. Для более чем двух вибраторов, размещенных в двумерной пространственной расстановке, можно выбирать углы, при которых улучшается подавление шума на низких пространственных частотах во всех пространственно-частотных направлениях.

Хотя можно просто выбирать фазовые углы матрицы, при которых обеспечивается приемлемая вариация шума в зависимости от пространственной частоты, в некоторых вариантах осуществления может быть предпочтительно иметь способ более объективного выбора углов. Этот выбор можно делать с помощью математической оптимизации.

При использовании пространственного спектра мощности шума для заданной целевой функции можно находить матрицу конкретного размера, которая минимизирует эту функцию. Если целевая функция является симметричной относительно к, это означает, что S не изменяется при изменении порядка следования столбцов на обратный (то есть, если одна строка матрицы суть (а, b … с), то Μ также содержит строку вида (с … b, а)).

Один пример целевой функции представлен для минимизации шума в пределах пространственных волновых чисел от -K до K, для некоторых K. Для получения некоторой стабилизации при всех волновых числах можно выполнять коррекцию путем добавления члена, зависящего от максимального шума, так, например

Для случая двух вибраторов, рассмотренного выше, на фиг. 4 показан оптимальный угол как функция граничной пространственной частоты К применительно к целевым функциям Е1 и Е2.

Этот же способ можно применять к большему количеству вибраторов и в различных расстановках. И опять, хотя выше приведены формулы для пространственных частот в одном направлении, аналогичные целевые функции могут быть получены путем замены одномерного пространственно-частотного интеграла в выражениях для E1 и Е2 двумерным интегралом в пределах подходящей области в пространственно-частотной плоскости.

Согласно другому примеру имеются три вибратора, каждый из которых возбуждает волны три раза, расположенных в линию при одинаковых расстояниях между вибраторами. Наличествует матрица S размером 3×3, которая имеет три выбираемых угловых параметра, обозначенных как α, β и γ:

Ha фиг. 5 результат такой оптимизации для матрицы 3×3 показан линиями углов α, β и γ для целевых функций Е1 и Е2. На фиг. 6 показано изменение пространственного волнового числа шума для оптимальных углов в соответствии с функцией Е2 для 6 значений K, нормированных относительно пространственной частоты Найквиста, а именно: 0,1; 0,25; 0,5; 0,75; 0,9 и 1. Кривая с наименьшим шумом при K=0 представлена для K=0,1, умноженного на частоту Найквиста, кривая со следующим наименьшим значением при K=0 представлена для K=0,25, умноженного на частоту Найквиста, и т.д. На фиг. 7 показаны такие же кривые для целевой функции Е1 (кривые расположены в аналогичном порядке). Таким образом, введение максимального члена в целевую функцию только ухудшает (несколько) характеристики при наименьших волновых числах, но значительно улучшает характеристики при высоких волновых числах.

Могут быть ситуации, когда сигнал имеет асимметричное пространственно-спектральное распределение. Например, если линия возбуждения волн продолжается к одной стороне расстановки геофонов, сигнал может полностью содержаться на одной стороне пространственного спектра. В этом случае диапазон пространственных частот, в пределах которого должна выполняться оптимизация, не будет симметричным относительно начала или, что эквивалентно, относительно площадных групп вибраторов, при этом двумерная пространственно-частотная область может не быть центрированной относительно начала. Когда положение вибраторов относительно приемников изменяют, диапазон пространственных частот, для которого относительные углы следует изменять, может меняться и, следовательно, когда вибраторы перемещают вдоль линии, относительные фазы также могут изменяться.

Чтобы переводить углы, получаемые при оптимизации, в вариации свип-сигналов, рассмотрим, например, ситуацию, когда наименьшее волновое число энергии продольных волн, вносящей вклад в изображение отражений, составляет 1/2000 с/м. Если вибраторы в группе разнесены на 25 м, то пространственная дискретизация при частотах ниже 40 Гц не приводит к наложению зеркальных частот. При параметрах свип-сигналов в пределах 8-80 Гц на нижнем конце диапазона свип-сигналов наибольшее пространственное волновое число, охватывающее данные, составляет 1/5 частоты Найквиста. В этом случае можно представить себе использование фаз матрицы, которое начинают с минимизации энергии пространственного шума с амплитудой меньше чем 1/5 частоты Найквиста, и изменяют фазы постепенно так, чтобы энергия пространственного шума в полосе частот сигналов минимизировалась по мере повышения частоты до 40 Гц, а шум был плоским по всему пространственно-частотному спектру. Поэтому, например, три вибратора с первоначальными углами α, β и γ следует выбрать на основании фиг. 5 и затем они должны подчиняться траекториям, например, близким к линиям Е2: α, Е2: β и Е2: γ по мере повышения частоты. Хотя изменение фазы происходит очень медленно (как это делается в некоторых вариантах осуществления), может иметься небольшое влияние на частотный спектр свип-сигнала, при быстрых изменениях и больших скоростях изменения фазы (как это делается в некоторых вариантах осуществления) могут добавляться изменения амплитуд в частотном спектре свип-сигнала.

Хотя в этом разделе для оптимизации использовались конкретные способы в области Фурье, можно использовать другие целевые функции, как в области Фурье, так и не в области Фурье.

Одна проблема, связанная с применением способов с одновременно работающими вибраторами, заключается в необходимости иметь дополнительное время по сравнению с исследованиями с единственным вибратором. Дополнительное время вытекает из двух обстоятельств. Во-первых, дополнительная длительность свип-сигнала необходима для компенсации меньшего подавления шума окружающей среды, когда применяют способы с одновременной работой вибраторов. Во-вторых, между многочисленными свип-сигналами необходимы многочисленные времена прослушивания.

При следовании свип-сигналов без паузы на время прослушивания между ударными воздействиями последовательности свип-сигналов в целом могут быть значительно укорочены. Однако издержкой этого может быть энергия гармоник от одного свип-сигнала, возникающая как шум относительно предшествующего свип-сигнала. Имеются схемы фазирования свип-сигналов, которыми можно исключать/уменьшать гармонический шум, возникающий относительно предшествующего свип-сигнала (перекрывающий шум) и относительно того же самого свип-сигнала (образование гармонических волн-спутников), путем фазового суммирования, при котором также получается матрица с одинаковыми особыми значениями. Однако будут некоторые затраты на подавление шума окружающей среды, поскольку требуется сопоставление синтетической последовательности (N+1) свип-сигналов с N свип-сигналами, фактически образуемыми, в результате чего шум окружающей среды возрастает приблизительно в соответствии с множителем 1+1/N (если большая часть шума окружающей среды является некогерентным шумом, создаваемым источником (например, двигателем вибратора), то возрастание не будет очень большим и маловероятно, что возникнут проблемы с отношением сигнала к шуму на приемниках).

В рамках того же общего направления, как при предшествующих вычислениях, можно рассмотреть матрицы фаз источников, которые не имеют одинаковых особых значений, но которые имеют хорошее подавление суммарного шума, адекватное разделение точек расположения отдельных источников (полного шума) и также подавление гармоник. Если можно переносить образование нормальных гармонических волн-спутников, то вместо использования последовательности (N+1) свип-сигналов можно рассмотреть снижение перекрывающего шума.

Из размерности задачи вытекает, что для получения значительного снижения гармонического шума в случае Μ вибраторов и Η гармоник можно свипировать по меньшей мере (M+H) раз.

Выбор правой функции стоимости и затем нахождение минимума (при типичном размере рассматриваемой матрицы) могут представлять трудности. Более сложными способами нелинейной условной оптимизации упрощается точное определение задачи (например, наложение ограничения на полный шум при минимизации суммарного и гармонического шумов). Например, для двух вибраторов со следующей матрицей фаз (7 свип-сигналов):

вибратор 1: -8,5; -153,3; 161,3; -157,2; -41,3; 73,8; -173,5,

вибратор 2: -44,3; -141,8; 117,8; -145,0; -35,5; 95,7; -18,3,

достигается подавление второй, третьей, четвертой и пятой гармоник на 13,6; 20,0; 4,2; и 26 дБ, соответственно, при этом суммарный шум на 0,75 дБ ниже, чем при синфазном свипировании, и полный шум на 2,3 дБ ниже, чем в случае матрицы с одинаковыми особыми значениями. Вместо использования подавления полного гармонического шума можно задавать дополнительный вес снижению гармонического шума на суммарных записях, что позволит достигать подавления при меньшем количестве свип-сигналов. Когда имеются фиксированные углы, не изменяющиеся в зависимости от частоты, способы, подобные описанным выше, можно использовать для поиска частотно-зависимого набора углов, в соответствии с которыми на низких частотах подавляются шум окружающей среды и гармонический шум при небольших волновых числах, а на высоких частотах получаются хорошие характеристики полного шума и подавляется полный гармонический шум. Поскольку гармонический шум возникает на различных частотах, получение соответствующих частотно-зависимых углов является сложной задачей. Например, при углах, используемых для 72 Гц, будет подавляться вторая гармоника шума, генерируемого при углах, используемых для 36 Гц, третья гармоника шума, генерируемого при углах, используемых для 24 Гц, четвертая гармоника шума, генерируемого в случае 12 Гц, и т.д. Кроме того, в одном варианте осуществления можно получать хорошие характеристики при полном подавлении гармоник, когда количество свип-сигналов составляет M+H+1 или больше. Однако для взаимосвязанных свип-сигналов имеются другие факторы, которые влияют на предпочтительное количество свип-сигналов и фазирование.

В случае фиксированного полного времени свипирования при полной амплитуде увеличение количества свип-сигналов будет сопровождаться увеличением полного времени для свип-сигналов, поскольку для каждого свип-сигнала потребуется время для линейного нарастания и время для линейного спада. В варианте осуществления максимальное количество свип-сигналов может быть меньше отношения полного времени свипирования ко времени прослушивания; в противном случае может потребоваться дополнительное время. Что касается перекрывающего шума, то часть сейсмической записи (наблюдаемая как частотно-временная плоскость), на протяжении которой присутствует перекрывающий шум, обратно пропорциональна длительности свип-сигнала и, следовательно, фиксированному полному времени свипирования. Она пропорциональна количеству свип-сигналов. Поэтому в варианте осуществления любое улучшение характеристик ослабления гармоник будет приводить к большему уравновешиванию избыточного гармонического шума, чем на это можно было рассчитывать. С другой стороны, как и в случае гармонического шума, если свип-сигналы начинаются слишком быстро, один после другого, шум возрастает вследствие реверберирующей поверхностной волны, сохраняющейся от предшествующего ударного воздействия. В дополнение к этому при коротких свип-сигналах имеется тенденция к ухудшению фазовой синхронизации и следовательно, избыточный перекрывающий шум, обусловленный отклонением от теоретической картины свипирования, будет возрастать. Поскольку отклонение возрастает линейно с числом гармоник, этот шум будет возрастать быстрее при гармониках высокого порядка. Однако при распределении полного времени свипирования по большему количеству свип-сигналов способами нелинейного подавления шума (такими как инверсия разновременности) снижают восприимчивость к импульсному шуму.

Часть описанного выше относится к подавлению гармонического шума от следующего свип-сигнала. При некоторых обстоятельствах гармонический шум от одного и того же свип-сигнала (гармонический шум волны-спутника) может быть проблематичным (например, в случае взаимосвязанных свип-сигналов, во время обычных исследований с временным интервалом прослушивания между свип-сигналами и т.д.). При этих обстоятельствах можно использовать аналогичную схему оптимизации, обеспечивающую при оптимизации подавление волны-спутника или подавление волны-спутника и перекрывающего шума.

Таким образом, при выборе (или свипировании от начала до конца) соответствующих фазовых углов можно регистрировать одновременные данные и применять коррекции статических свойств и различий сигнатур источников до перекомпоновки сгруппированных данных с контролируемым влиянием на подавление шума окружающей среды в отличие от обычных сгруппированных данных при аналогичном продолжительном возбуждении волн. При использовании изменяющихся с частотой фазовых углов и одновременном возбуждении волн можно обеспечивать почти такое же подавление шума окружающей среды на низких пространственных частотах (или по меньшей мере положительную динамику), какое получается при сгруппированных данных (при этом также обеспечивается подавление поверхностной волны за счет лучшей пространственной дискретизации). Наконец, включение гармонического перекрывающего шума в оптимизацию открывает перспективы снижения времени исследований почти до времени при обычном свипировании (но с преимуществами исследований с точечными источниками и контролируемым перекрывающим шумом в исходных данных).

Как показывалось в этой заявке, вариант осуществления включает в себя способ, содержащий одновременное образование первого и второго сейсмических свип-сигналов с относительным сдвигом фаз (например, Θ(t)) относительно друг друга. Сдвиг фаз изменяют во время одновременного свипирования. Сдвиг фаз можно плавно повышать или понижать на всем протяжении или на участках свип-сигналов. Однако сдвиг фаз может иметь переменную скорость возрастания или снижения. Некоторые изменения могут быть оперативными (например, мгновенный скачкообразный переход к заметно выраженной другой скорости). Изменение фаз можно осуществлять любым из нескольких способов, в соответствии с которыми имеются два свип-сигнала, которые перекрываются (в течение короткого време