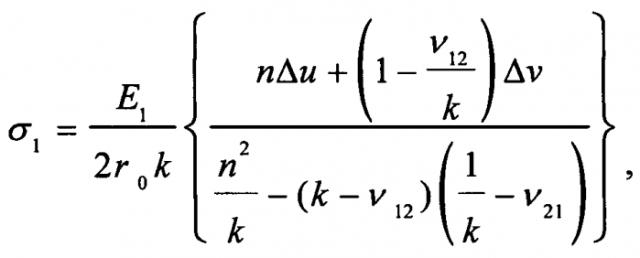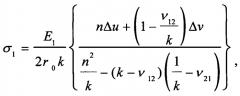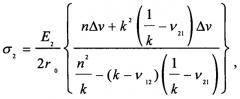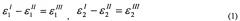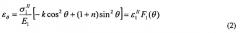Способ определения остаточных напряжений в композиционных материалах

Способ определения остаточных напряжений в композиционных материалах

Иллюстрации

Показать все

Реферат

Изобретение относится к области экспериментальной механики и предназначено для определения остаточных напряжений, возникающих при изготовлении тонкостенных конструкций летательных аппаратов из ортотропных композиционных материалов.

Известен способ для определения остаточных напряжений в композиционных материалах с помощью метода сверления отверстия, по которому на поверхности образца в виде пластины прямоугольной формы закрепляют розетку из трех тензодатчиков, высверливают в центре симметрии этой розетки сквозное круговое отверстие, измеряют деформации, вызванные локальным удалением материала при сверлении, в местах установки каждого тензодатчика и вычисляют компоненты остаточных напряжений согласно соотношениям анизотропной теории упругости (Pagliaro P, Zuccarello В. Residual stress analysis of orthotropic materials by the through-hole drilling method. Experimental Mechanics 2007; 47 (2): 217-236). Причиной возникновения деформаций в местах установки тензодатчиков является высвобождение энергии остаточных напряжений вследствие локального удаления материала. Недостатком данного способа является то, что при его применении измерения проводятся в ограниченном числе точек, расположенных вне контура отверстия, координаты которых по отношению к главным осям анизотропии не известны перед проведением эксперимента, что приводит к необходимости использования сложного численного моделирования для определения калибровочных коэффициентов, связывающих измеряемые деформации и искомые величины остаточных напряжений, увеличивая тем самым погрешность определения компонент остаточных напряжений.

Для повышения точности конечных результатов были разработаны оптические интерференционные методы, которые обеспечивают измерение полей тангенциальных компонент перемещений поверхности вне контура зондирующего отверстия. В подобных случаях для определения остаточных напряжений используется многоточечный подход, основанный на обработке избыточного массива исходных данных. При этом обеспечивается минимизация погрешности между экспериментальными данными и их численным представлением с помощью метода наименьших квадратов (Cardenas-Garcia JF, Preidikman S, Shabana YM. Solution of the moire hole drilling method using a finite-element-method-based approach. International Journal of Solids and Structures 2006; 46 (22-23): 6751-6766).

Наиболее близким техническим решением, выбранным в качестве прототипа предлагаемого способа, является способ определения остаточных напряжений в ортотропных композитных пластинах, заключающийся в том, что образец в виде прямоугольной пластины устанавливают в оптическую схему интерферометра, регистрируют распределение фазы отраженной волны, соответствующее поверхности образца в исходном состоянии, высверливают зондирующие отверстие, возвращают образец в оптическую схему, регистрируют распределение фазы отраженной волны, соответствующее деформированной поверхности образца, получают распределение фаз отраженной волны, соответствующее разнице двух состояний, измеряют значения фазы этой волны для N точек (N>100) в окрестности отверстия, преобразуют значения фазы волны во всех точках в величины компонент тангенциальных перемещений, определяют с помощью теории упругости анизотропного тела и численного моделирования калибровочные коэффициенты, необходимые для пересчета измеренных компонент тангенциальных перемещений в величины компонент остаточных напряжений. После этого искомые компоненты остаточных напряжений определяются как решение переопределенной системы алгебраических уравнений на основе метода наименьших квадратов.

Существующие методы основаны на сложном конечно-элементном моделировании и приближенном решении обратной задачи, механическая формулировка которой для ортотропных композиционных материалов часто связана с преодолением значительных математических проблем и всегда требует анализа соотношения между постоянными упругости (Cardenas-Garcia JF, Ekwaro-Osire S, Berg JM, Wilson WH. Nonlinear least-square solution to the moire hole method problem in orthotropic materials. Part I: Residual stresses. Experimental Mechanics 2005; 45 (4): 301-313). Дело в том, что теоретическое решение задачи о концентрации напряжений/деформаций в окрестности сквозного отверстия в ортотропной пластине при ее одноосном растяжении под произвольным углом к главным осям анизотропии существует только для контура отверстия (Лехницкий С.Г. Теория упругости анизотропного тела. 2-е издание. - М.: Наука, 1977, 416 с.). Экспериментальная реализация существующих методов требует использования оптических схем, необходимыми элементами которых являются сложные приборы и устройства для автоматического измерения фазового распределения оптических волн в фиксированных точках поверхности.

Техническим результатом данного изобретения является повышение точности измерения остаточных напряжений, а также повышение ресурса и надежности элементов конструкций из композиционных материалов при их эксплуатации за счет учета остаточных напряжений при анализе напряженно-деформированного состояния.

Технический результат достигается тем, что в способе определения остаточных напряжений в композиционных материалах, включающем установку исследуемого образца в оптическую схему интерферометра, регистрацию исходного состояния спекл-структуры поверхности высокоразрешающей видеокамерой, удаление образца из оптической схемы, высверливание сквозного зондирующего отверстия, возвращение образца в оптическую схему, регистрацию спекл-структуры деформированного состояния поверхности, визуализацию картин интерференционных полос путем численного вычитания двух пар изображений, определение величин двух тангенциальных компонент перемещений в окрестности отверстия, в процессе обработки экспериментальных данных определяют приращения диаметров зондирующего отверстия в направлении главных остаточных напряжений σ₁ и σ₂, и определяют значения главных остаточных напряжений по формулам:

где E₁, E₂ - наибольший и наименьший по величине главные модули упругости композиционного материала; ν₁₂, ν₂₁ - коэффициенты Пуассона композиционного материала; k = E 1 / E 2 , n = 2 ( k + 1 ) ; 2r₀ - диаметр зондирующего отверстия; Δu и Δν - приращения диаметра зондирующего отверстия в направлении главных остаточных напряжений σ₁ и σ₂ соответственно.

Техническое решение поясняется следующими чертежами.

Фиг. 1 - представлена схема определения коэффициентов концентрации деформаций на контуре сквозного отверстия в ортотропной пластине при ее растяжении в направлении модуля упругости E₁.

Фиг. 2 - представлена схема определения коэффициентов концентрации деформаций на контуре сквозного отверстия в ортотропной пластине при ее растяжении в направлении модуля упругости E₂.

Фиг. 3 - представлена общая схема спекл-интерферометра для определения тангенциальной компоненты перемещений u в направлении модуля упругости E₁.

Фиг. 4 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты перемещения u и схема получения исходной экспериментальной информации.

Фиг. 5 - представлена картина реальных интерференционных полос, полученная в терминах тангенциальной компоненты перемещения ν и схема получения исходной экспериментальной информации.

Фиг. 6 - представлены результаты определения остаточных напряжений в ортотропной композиционной пластине.

Фиг.7 - представлена картина образцовых интерференционных полос, полученная в терминах тангенциальной компоненты перемещения u.

Фиг. 8 - представлена картина образцовых интерференционных полос, полученная в терминах тангенциальной компоненты перемещения ν.

На фиг. 1 представлена схема прямоугольной пластины 1 с зондирующим отверстием 2, которая используется для определения коэффициентов концентрации деформаций при ее растяжении в направлении наибольшего модуля упругости E₁. На фиг. 2 представлена схема прямоугольной пластины 1 с зондирующим отверстием 2, которая используется для определения коэффициентов концентрации деформаций при ее растяжении в направлении наименьшего модуля упругости E₂. Эти коэффициенты концентрации деформации используются для определения главных компонент остаточных напряжений по данным измерений приращений диаметров зондирующего отверстия следующим образом.

Формулировка метода сверления отверстия дает следующие соотношения между величинами главных компонент деформаций на контуре отверстия:

Верхние индексы в соотношениях (1), обозначенные римскими цифрами, относятся к механическому состоянию поверхности объекта. Состояние I соответствует двухосному нагружению элемента объема материала, содержащего зондирующее отверстие. Состояние II представляет собой исходное деформированное состояние поверхности, вызванное двухмерным полем остаточных напряжений перед сверлением отверстия. Компоненты этого поля напряжений, которые представляют собой главные остаточные напряжения σ 1 I I и σ 2 I I , и должны быть определены по результатам эксперимента. Состояние III соответствует высвобождению энергии остаточных напряжений после сверления отверстия и может быть представлено как разность между состояниями I и II. Необходимые параметры состояния III должны быть получены по картинам интерференционных полос, а для состояний I и II заданы аналитически или численно, используя общие положения теории упругости.

Главные деформации ε 1 I и ε 2 I для состояния I могут быть выражены в форме решения упругой задачи о концентрации напряжений. Используемый далее подход основан на решении С.Г. Лехницкого для ортотропного материала, которое описывает распределение деформаций в прямоугольной пластине с центральным сквозным отверстием при одноосном растяжении для различной ориентации направления растягивающего усилия по отношению к направлениям главных осей анизотропии (Лехницкий С.Г. Теория упругости анизотропного тела. 2-издание. - М.: Наука, 1977. - 416 с.). Здесь и далее декартова система координат (x, y) определяет главные оси анизотропии, причем ось x совпадает с направлением большего по величине модуля упругости E₁. Полярный угол θ, который всегда отсчитывается от пересечения контура отверстия с направлением оси x, определяет позицию точки на контуре отверстия. Для тонкой пластины с круговым отверстием, растягиваемой номинальными напряжения σ 1 I I в направлении модуля упругости E₁ (фиг. 1), распределение окружной деформации вдоль контура отверстия можно записать, как:

Для тонкой пластины с круговым отверстием, растягиваемой номинальными напряжениями σ 2 I I в направлении модуля упругости E₂ (фиг. 2), распределение окружной деформации вдоль контура отверстия имеет вид:

где

Соотношения (2) и (3) с учетом принципа суперпозиции обеспечивают определение коэффициентов концентрации деформаций в точке А (θ=0) и в точке В (θ=π/2), которые необходимы для построения соотношений типа (1):

Чтобы сформировать левую часть основного уравнения метода сверления отверстия (1), необходимо выразить исходные деформации в точках А и В перед сверлением отверстия. Эти деформации вытекают из закона Гука для плоского напряженного состояния:

При выводе соотношений (6) используется известная формула:

Соотношения (5) и (6) формируют левую часть системы уравнений (1), которая необходима для определения компонент остаточных напряжений в тонкой ортотропной пластине при сверлении сквозного отверстия.

Формирование правой части системы линейных алгебраических уравнений (1) основывается на ряде положений теории упругости, которые вытекают из вида функций концентрации деформаций (2) и (3). Во-первых, для состояния I тангенциальные перемещения u и ν на контуре малого отверстия радиусом r₀, согласно соотношениям (5), можно представить в следующем виде:

Соотношения (7) дают возможность получить распределение окружной деформации ε θ I вдоль контура центрального кругового отверстия радиусом r₀ в тонкой пластине:

Комбинация выражений (7) и (8) для θ=0 и θ=π/2 позволяет установить, что:

где Δu^I=2u^I(θ=0) и Δν^I=2ν^I(θ=π/2) представляют собой приращения диаметров реального отверстия диаметром 2r₀, вызванного двухосным нагруженном пластины в направлении главных осей анизотропии E₁ и E₂ соответственно.

Аналогичным путем с использованием соотношений (6) можно получить, что

где Δu^II=2u^II(θ=0) и Δν^II=2ν^II(θ=π/2) представляют собой приращения диаметров условного отверстия диаметром 2r₀, вызванного двухосным нагруженном пластины в направлении главных осей анизотропии E₁ и E₂ соответственно.

Разница соотношений (9) и (10) дает правую часть системы уравнений (1):

где Δu и Δν - приращения диаметров отверстия диаметром 2r₀, просверленного в двумерном поле напряжений, в направлениях главных осей анизотропии E₁ и E₂ соответственно. Требуемые величины приращений диаметров отверстия Δu и Δν экспериментально определяют методом электронной спекл-интерферометрии. Подстановка соотношений (2) и (3) в соотношения (11) определяет явный вид системы уравнений (1) в случае, когда главные направления остаточных напряжений (деформаций) совпадают с главными направлениями анизотропии ортотропной пластины:

Решение системы линейных алгебраических уравнений (12) дает две необходимые компоненты остаточных напряжений и имеет следующий вид:

Величины компонент остаточных напряжений σ₁ и σ₂ (13) представляют собой единственное решение корректно сформулированной обратной задачи, что обеспечивает минимально возможную погрешность их определения (Lankaster P. Theory of matrices. New York-London: Academic Press, 1969).

Величины приращений диаметров отверстия Δu и Δν, которые необходимы для определения компонент остаточных напряжений согласно формулам (13), экспериментально определяют методом электронной спекл-интерферометрии с помощью оптической схемы с двумя симметричными направлениями освещения 3 и нормальным по отношению к плоской поверхности объекта направлением наблюдения, определяемым положением высокоразрешающей видеокамеры 4 (фиг. 3). Два изображения исследуемого участка поверхности, соответствующие исходному и конечному механическому состоянию пластины 1 со сквозным отверстием 2, последовательно регистрируют высокоразрешающей видеокамерой 4 и сохраняют в виде цифровых файлов. Визуализацию картин интерференционных полос осуществляют путем цифрового вычитания соответствующих изображений.

Когда проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси x, то картина интерференционных полос, соответствующая тангенциальной компоненте перемещений u в направлении модуля упругости E₁, описывается следующим образом:

где N_u=±1; ±2; ±3, … - абсолютные порядки интерференционных полос; λ - длина волны лазерного освещения; Ψ=π/4 - угол между наклонным направлением освещения и нормальным к поверхности плоского объекта направлением наблюдения. Тангенциальную компоненту перемещения ν в направлении модуля упругости E₂ определяют аналогичным способом. Одновременное определение обеих плоских компонент перемещений u и ν обеспечивают включением двух оптических схем в единую установку. Идентификация физического знака компонент перемещений проводят методом регистрации интерферограмм с дополнительным фазовым сдвигом, направление которого задают известным образом (Pisarev VS, Odintsev IN, Apalkov AA, Chemov AV. Role of high-quality interference fringe patterns for the residual stress determination by the hole-drilling method / Visualization of Mechanical Processes 2011; Vol. 1. N 1. DOI: 10.1615 / VisMechProc.v1.i1.40).

Реализация предлагаемого способа осуществляется следующим образом.

Исследуемый образец в виде прямоугольной пластины, изготовленной из композиционного материала (фиг. 1, фиг. 2), устанавливают на фиксированной позиции в оптической схеме интерферометра (фиг. 3) с помощью кинематического устройства (Maclead N, Kapur DN. A kinematically designed mount for the precise location of specimen for holographic interferometry. Journal of Physics E: Scientific Instruments 1973; 6: 423-424). Освещают поверхность образца двумя плоскими волнами 3 (фиг. 3), так, что проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси x, и регистрируют спекл-структуру поверхности пластины 1 в исходном состоянии, необходимую для определения компоненты перемещений u (цифровой файл U1). Освещают поверхность образца двумя плоскими волнами по двум симметричным направлениям освещения 3 (фиг. 3), так, что проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси y, и регистрируют спекл-структуру поверхности пластины 1 в исходном состоянии, необходимую для определения компоненты перемещений ν (цифровой файл V1). Удаляют образец из оптической схемы интерферометра. Высверливают сквозное отверстие 2 диаметром 2r₀. Возвращают образец в оптическую схему интерферометра. Освещают поверхность образца двумя плоскими волнами 3 (фиг. 3), так, что проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси y, и регистрируют спекл-структуру поверхности пластины 1 в деформированном состоянии, необходимую для определения компоненты перемещений ν (цифровой файл V2). Освещают поверхность образца двумя плоскими волнами 3 (фиг. 3), так, что проекция направления освещения на плоскую поверхность исследуемого объекта совпадает с направлением оси x, и регистрируют спекл-структуру поверхности пластины 1 в деформированном состоянии, необходимую для определения компоненты перемещений u (цифровой файл U2). Последовательно проводят численное вычитание файлов U2-U1 и тем самым V2-V1 визуализируют картины интерференционных полос, по которым определяют приращения диаметров отверстия Δu и Δν, необходимые для определения компонент остаточных напряжений согласно формулам (13).

Предлагаемым способом проводилось определение остаточных напряжений в прямоугольной пластине размерами 400×200×6 мм³, изготовленной из ортотропного композиционного материала. Направление модуля упругости E₁ (x) и E₂ (y) совпадает с длинным и коротким краем пластины соответственно. Обобщенные характеристики жесткости пакета и параметры анизотропии материала имеют следующие значения:

Зачетный ряд из девяти сквозных отверстий расположен вдоль линии, которая совпадает с направлением E₂ на расстоянии 150 мм от правого края образца (x=50 мм, фиг. 1-2). Расстояние между соседними отверстиями составляет величину не менее 15-ти мм. Источником когерентного освещения служит малоразмерный диодный лазер с длиной волны λ=532 нм. Картины интерференционных полос регистрируют с помощью классической схемы спекл-интерферометра (фиг. 3). На фиг. 4 и фиг. 5 показаны картины интерференционных полос, полученные в точке с координатами (x=50 мм, y=0) для тангенциальной компоненты перемещений u и ν, соответственно. Горизонтальная ось симметрии на фиг. 4 и вертикальная ось симметрии на фиг. 5 совпадают с главными направлениями анизотропии E₁ и E₂, соответственно. Необходимо отметить высокое качество представленных интерферограмм. То же самое относится ко всем картинам полос, полученных для остальных отверстий. Идентификация физического знака компонент перемещений свидетельствует, что диаметр отверстия увеличивается как в направлении оси x (модуль упругости E₁, тангенциальная компонента перемещений u), так и в направлении оси y (модуль упругости E₂, тангенциальная компонента перемещений ν).

Приращения диаметров отверстия Δu и Δν, которые являются исходными экспериментальными данными, определяют следующим образом согласно формуле (14).

где ΔN_u и ΔN_ν представляют собой разности абсолютных порядков полос, которые подсчитывают на одной интерферограмме между двумя базисными точками в направлении главных остаточных напряжений σ₁ и σ₂ соответственно. Две базисные точки определяют, как точки пересечения диаметра отверстия в соответствующем направлении главного напряжения с контуром отверстия (фиг. 4 и фиг. 5). На фиг. 4 показаны две базисные точки 1′ и 2′, а также схема подсчета разности абсолютных порядков полос ΔN_u=10,0. На фиг. 5 показаны две базисные точки 3′ и 4′, а также схема подсчета разности абсолютных порядков полос ΔN_ν=13,0. Полученные значения Δ N u E x p = 10,0 и Δ N ν E x p = 13,0 подставляют в формулы (16) и определяют величины приращения диаметров отверстия Δu=3,80 мкм, Δν=4,94 мкм, которые совместно с величинами обобщенных параметров упругости (15) подставляют в формулы (13) и определяют величины главных компонент остаточных напряжений σ 1 E x p = 73,4   М П а , σ 2 E x p = 61,4   М П а .

Фиг. 6 демонстрирует результаты определения компонент главных остаточных напряжений σ₁ и σ₂ для всех исследованных точек. Маркеры в виде «прозрачных» квадрата и треугольника обозначают компоненты остаточных напряжений σ₁ и σ₂ соответственно для отверстий диаметром 2r₀=2,0 мм. Маркеры в виде «закрашенных» квадрата и треугольника обозначают компоненты остаточных напряжений σ₁ и σ₂ соответственно для отверстий диаметром 2r₀=2,5 мм. Полученные величины выявляют совпадение между собой в пределах 20-ти процентов главной компоненты остаточных напряжений σ₁ и в пределах 13-ти процентов главной компоненты остаточных напряжений σ₂ для разных точек поверхности образца 1, что подтверждает высокие метрологические характеристики предлагаемого способа.

Величины погрешностей определения главных компонент остаточных напряжений оценивают путем построения и визуализации образцовых картин интерференционных полос (Pisarev VS, Balalov VV, Aistov VS, Bondarenko MM, Yustus MG. Reflection hologram interferometry combined with hole drilling techniques as an effective tool for residual stress field investigation in thin-walled structures. Optics and Lasers in Engineering 2001; 36 (6): 551-597). Для этого используют квадратную ортотропную пластину размерами 80×80×6 мм³ с центральным сквозным отверстием диаметром 2r₀=2.5 мм и такую же пластину без отверстия. Обобщенные параметры упругости пластины соответствуют значениям (15). Численное моделирование полей тангенциальных компонент перемещений на поверхности образца проводят на основе программного комплекса MSC/NASTRAN. Конечно-элементную сеть формируют из 20000 элементов типа QUAD 4. Расчетные величины деформаций на контуре отверстия при двухосном растяжении совпадают с аналогичными данными аналитических зависимостей (5) в пределах пяти процентов. Визуализацию образцовых картин полос осуществляют для величин компонент остаточных напряжений, соответствующих точке с координатами x=50 мм, y=0 (фиг. 1-3), согласно уравнениям (1) и формуле (14). На фиг. 7 и фиг. 8 показаны образцовые картины интерференционных полос для тангенциальных компонент перемещений u и ν соответственно. Искусственные изображения на фиг. 7 и фиг. 8 моделируют реальные интерферограммы, показанные на фиг. 4 и фиг. 5 соответственно.

Оценку погрешностей определения главных компонент остаточных напряжений проводят путем сравнения экспериментально полученных разностей порядков полос в направлении главных остаточных напряжений и аналогичных данных, относящихся к искусственным интерференционным изображениям. Эти параметры равны Δ N u E x p = 10,0 ; Δ N ν E x p = 13,0 и Δ N u N u m = 10,0 ; Δ N ν N u n = 12,0 . Величины разностей абсолютных порядков полос для компоненты перемещений u, полученные двумя способами, полностью совпадают. Разница в величинах разностей абсолютных порядков полос для компоненты ν составляет одну полосу.

Значения Δ N u N u m = 10,0 и Δ N ν N u n = 12,0 подставляют в формулы (16) и определяют величины приращения диаметров отверстия Δu=3,80 мкм, Δν=4,56 мкм, которые совместно с величинами обобщенных параметров упругости (15) подставляют в формулы (13) и определяют величины главных компонент остаточных напряжений, соответствующие образцовым картинам интерференционных полос σ 1 N u m = 73,4   М П а , σ 2 N u m = 61,4   М П а . Величины главных компонент остаточных напряжений, полученные двумя способами, используют для оценки относительной погрешности в определении каждой компоненты остаточных напряжений следующим способом:

Оценки реальных погрешностей (17), основанные на построении образцовых картин интерференционных полос, доказывают, что эти погрешности не превышают шести процентов. Такая точность с гарантией достигается в случае, когда разности порядков полос идентифицируются невооруженным глазом оператора вследствие того, что величина погрешности δN=0.5 полосы означает разницу между соседними светлой и темной полосами. Таким образом, предлагаемый способ, который не требует привлечения специального оборудования для автоматической регистрации полей перемещений, обеспечивает точность определения остаточных напряжений в ортотропных композиционных материалов, достаточную для большинства реальных инженерных задач.

Этот технический результат достигается за счет того, что при способе определения остаточных напряжений в ортотропных композиционных пластинах, включающем установку образца в виде прямоугольной пластины в оптическую схему интерферометра, регистрацию спекл-структуры на поверхности образца в исходном состоянии высокоразрешающей видеокамерой, удаление образца из оптической схемы интерферометра, высверливание зондирующего отверстия, возвращение образца в исходное положение, регистрацию спекл-структуры деформированной поверхности образца, визуализацию картин интерференционных полос путем численного вычитания двух полученных ранее изображений, определение приращения диаметров зондирующего отверстия в направлении главных остаточных напряжений, при этом вычисление компонент главных остаточных напряжений осуществляется по формулам, вытекающим из теоретического решения о концентрации напряжений на контуре сквозного кругового отверстия в пластине при ее растяжении в произвольном направлении по отношению к главным осям анизотропии, что исключает необходимость численного моделирования при переходе от измеряемых параметров к величинам остаточных напряжений и тем самым обеспечивает существенное повышение точности и надежности результатов определения главных компонент остаточных напряжений.

Технический результат также достигается тем, что для определения компонент остаточных напряжений исходные экспериментальные данные устанавливают без применения сложных средств автоматического измерения фазы отраженной оптической волны. Формулы, связывающие исходные экспериментальные данные с искомыми компонентами остаточных напряжений, представляют собой единственное решение корректно сформулированной обратной задачи, которое обеспечивает максимальную возможную точность определения компонент остаточных напряжений (Laermann KH. Reliable evaluation of measured data-an inverse problem. In: Juptner W, Osten W, Editors. Fringe 2001. Proc. of the 4th Int. Workshop on Automatic Processing of Fringe Patterns. Paris: Elsevier, 2001. p. 443-450). Это означает также, что отсутствует необходимость привлечения метода конечных элементов для вычисления калибровочных коэффициентов и применения переопределенных многоточечных алгоритмов на основе метода наименьших квадратов. Формулировка экспериментального метода не зависит от механических свойств ортотропного материала.

Способ определения остаточных напряжений в композиционных материалах, включающий установку исследуемого образца в оптическую схему интерферометра, регистрацию исходного состояния спекл-структуры поверхности высокоразрешающей видеокамерой, удаление образца из оптической схемы, высверливание сквозного зондирующего отверстия, возвращение образца в оптическую схему, регистрацию спекл-структуры деформированного состояния поверхности, визуализацию картин интерференционных полос путем численного вычитания двух пар изображений, определение величин двух тангенциальных компонент перемещений в окрестности отверстия, отличающийся тем, что в процессе обработки экспериментальных данных определяют приращения диаметров зондирующего отверстия в направлении главных остаточных напряжений σ₁ и σ₂, и определяют значения главных остаточных напряжений по формулам: где E₁, E₂ - наибольший и наименьший по величине главные модули упругости композиционного материала; ν₁₂, ν₂₁ - коэффициенты Пуассона композиционного материала; , ; 2r₀ - диаметр зондирующего отверстия; Δu и Δν - приращения диаметра зондирующего отверстия в направлении главных остаточных напряжений σ₁ и σ₂ соответственно.