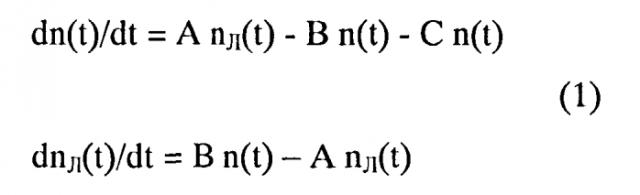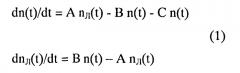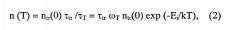Диэлектрический метод диагностики электронных состояний в кристаллах силленитов

Диэлектрический метод диагностики электронных состояний в кристаллах силленитов

Иллюстрации

Показать все

Реферат

Изобретение относится к области инновационных технологий и может быть использовано для определения параметров кристаллов силленитов, определяющих эффективность перспективных технических систем, и их экспресс-характеризации методами диэлектрической спектроскопии.

Интерес к кристаллам силленитов обусловлен уникальным сочетанием их физических свойств: удобством синтеза кристаллических образцов большого размера, высокой оптической прозрачностью в видимом и ближнем ИК-диапазонах, рекордно высоким темновым сопротивлением, большой фоточувствительностью, наличием ярких электрооптических эффектов и, наконец, большой естественной оптической активностью. Все это позволяет использовать данные соединения в качестве активных сред для записи, обработки и хранения оптической информации, включая высокоинформативную голографическую запись [1].

Известен способ измерения фотоэлектрических параметров, заключающийся в измерении скорости релаксации объемных фазовых голограмм [2]. При этом непосредственно измеряемой величиной является дифракционная эффективность объемной голограммы, записанной в образце за счет диффузионного или дрейфового механизма. В отсутствие внешнего поля процесс релаксации голограммы происходит по экспоненциальному закону с характерным временем τ s c = τ M ( 1 + K 2 L D 2 ) , где К - пространственная частота записанной голограммы, τ_M - время максвелловской релаксации, L_D - диффузионная длина переноса носителей заряда. В присутствии внешнего поля процесс релаксации приобретает осциллирующий характер с частотами колебаний ω_scw=(τ_MKL₀)^-1, ω_dr=КµЕ₀, где L₀ - дрейфовая длина носителей заряда в электрическом поле с напряженностью Е₀. Измерение характерных времен и частот релаксационных процессов позволяет определить удельную фотопроводимость, время максвелловской релаксации и дрейфовую подвижность носителей заряда. Недостаток данного метода - очень узкая применимость.

Известен способ определения фотопроводимости и времени ее релаксации, при котором поверхность полупроводника освещается амплитудно-модулированным пучком света [3]. К образцу прикладывается постоянное напряжение от внешнего источника. Отклик материала регистрируется в виде фототока, возникающего в объеме кристалла. По амплитуде сигнала в области низких частот модуляции и по виду амплитудно-частотной характеристики определяются величина оптически индуцированной электропроводности и время релаксации фотопроводимости. Недостатком способа является то, что величина удельной фотопроводимости не измеряется непосредственно, а рассчитывается с учетом геометрических размеров образца и условий освещения, что вносит дополнительную погрешность.

Цель изобретения - создание метода оценки параметров, характеризующих оптоэлектронные свойства силленитов, по результатам измерений частотных зависимостей проводимости, комплексной диэлектрической проницаемости и тангенса угла диэлектрических потерь при разных температурах.

Технический результат изобретения достигается путем предварительной обработки кристаллов, исключающей искажение данных, а также за счет разработанной математической модели, позволяющей определить значения оптоэлектронных параметров путем сравнения теории с экспериментом.

Исследования проводились на единообразно подготовленных к опытам образцах BSO (что обеспечивало надежную воспроизводимость результатов), выращенных методом Чохральского, имевших размеры 10×10×1 мм и обладавших темповым удельным сопротивлением порядка 10¹³ Ом · м.

Алгоритм подготовки сводился к тому, что образец вначале нагревался от комнатной температуры до температуры +150°С с целью опустошения ловушек различного типа, присутствующих в кристалле, после чего охлаждался до исходной температуры -70°С, затем освещался в течение 20 минут фотоактивным светом (λ=470 нм) фиксированной интенсивности и выдерживался в темноте после выключения подсветки в течение 20 минут для исключения возможного влияния на результаты измерений активности сверхмелких ловушек. После этого проводились измерения при медленном (5,2°С/мин) нагревании образца от -70°С до +150°С.

Измерения величины термостимулированных токов (ТСТ) производились на диэлектрическом спектрометре марки «Alpha-Beta Impedance Analizer» фирмы Novocontrol Technologies на двух частотах: 10 Гц и 100 Гц. Температура образца Т при измерениях ТСТ изменялась от -70°С до +150°С с постоянной скоростью 5,2°С/мин. Кроме того, производились измерения температурных и частотных зависимостей тангенса угла диэлектрических потерь, а также действительной и мнимой частей диэлектрической проницаемости образцов в частотном диапазоне 10^-2 Гц до 10⁵ Гц.

В процессе исследований образец помещался между обкладками простейшего конденсатора. Измерялась амплитуда тока через образец I_o при подаче на него синусоидального напряжения U(t) и разность фаз φ между колебаниями U(t) и I(t). С помощью конвертора эти данные с применением разработанных фирмой Novocontrol Technologies компьютерных программ преобразовывались в данные о физических характеристиках образца. При анализе экспериментальных данных использовались результаты выполняемого диэлектрическим спектрометром расчета проводимости и электрической емкости образца согласно следующей последовательности. На начальном этапе вычислялись значения действительной и мнимой частей диэлектрической проницаемости согласно выражениям:

|ε′|=I_otgφ/[(1+tg²φ)^1/2ωC_oU_o] и |ε′′|=|ε′|/tgφ,

где ω - частота регистрации, С_о - емкость пустой измерительной ячейки. Это позволяет на последующем этапе вычислять величину максвелловского времени релаксации τ:

τ=R_xC_x=|ε′|/|ε′′|ω,

где R_x - электрическое сопротивление, R_x=τ/С_о|ε′|; С_х - электрическая емкость образца, С_х=τ/R_x.

Перечень фигур

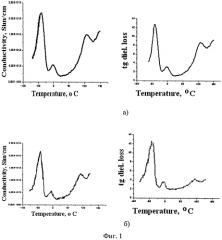
Фиг. 1а, б. Температурные зависимости проводимости и тангенса угла диэлектрических потерь образцов BSO на частотах 100 Hz (а) и 10 Hz (б) соответственно.

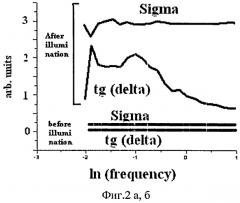
Фиг. 2а, б. Низкочастотные части образцов BSO диэлектрических спектров при температуре 0°С, полученные как до, так и после фотоактивной засветки, соответственно.

Фиг. 3а, б, в. Схема уровней локальных центров в BSO, включающая два уровня ловушек tr1 и tr2 (из которых уровень tr2 расположен глубже tr1), а также глубокий уровень рекомбинации R.

Фиг. 4. Определение энергии ионизации примесных центров в кристаллах BSO методом ТСТ с помощью диэлектрического спектрометра.

Так как при измерении ТСТ на частотах 10 Гц и 100 Гц реализуются малые концентрации свободных электронов n(t) в зоне проводимости, при которых максвелловское время релаксации τ_М велико и находится в диапазоне от десятков до сотен секунд, то приведенные на фиг. 1а и 1б результаты измерений ТСТ отражают неискаженное значение n(t). Об этом свидетельствует также сравнение диэлектрических спектров фиг. 2а и 2б, полученных как до, так и после фотоактивной засветки. Эти рисунки показывают, что только для низких частот, меньших 1 Гц, наблюдается вызванное засветкой изменение ДС спектров в связи с уменьшением максвелловского времени, обусловленное ростом n(t) при засветке образца.

Известно, что кристалл ВSO является высокоомным фотопроводником, электрооптические свойства которого позволяют за счет поперечного электрооптического эффекта непосредственно наблюдать эволюцию области пространственного заряда в объеме кристалла [4], а именно в [4] наблюдалось изменение ширины области пространственного заряда в условиях предварительного освещения кристалла BSO светом, генерирующим свободные носители, и последующего приложения к нему тянущего электрического поля после выключения генерирующего света. Также в запрещенной зоне кристаллов BSO имеются как уровни ловушек, так и глубоких центров рекомбинации [1, 5, 6]. Исходя из наличия двух максимумов ТСТ, для интерпретации результатов используется схема (фиг. 3), включающая два уровня ловушек tr1 и tr2 (из которых уровень tr2 расположен глубже tr1), а также глубокий уровень рекомбинации R.

В соответствии с алгоритмом проведения нашего эксперимента предварительный прогрев образца до 150°С приводит к полному опустошению ловушек и рекомбинации электронов с дырками на R-центрах. Охлаждение образца в темноте до температуры -70°С и его выдерживание в темноте при этой температуре создает предпосылки для унификации условий эксперимента и обеспечения воспроизводимости результатов.

При последующем освещении при низких температурах (-70°С) образца BSO фотоактивным светом (λ=470 нм) фиксированной интенсивности в течение 20 минут электроны в рамках предлагаемой схемы переходят с R-центров через зону проводимости на ловушки, заполняя их - фиг. 3а. Последующая выдержка образца в темноте фиксирует метастабильное квазиравновесное состояние, так что концентрация электронов в зоне проводимости очень мала. Поэтому при приложении внешнего переменного напряжения регистрируемый ток также мал. Однако при повышении температуры с постоянной скоростью b=5,2°С/мин постепенно ионизируются мелкие tr1 ловушки, генерируя носители заряда в зоне проводимости, что приводит к появлению ТСТ.

При той температуре, при которой kT близко к энергии ионизации (E_i1) tr1-ловушек, возникает начальный подъем ТСТ. Для данного типа ловушек дрейф свободных электронов во внешнем электрическом поле сопровождается, по данным электрооптических измерений [4], эффективным перезахватом электронов на ловушки и слабым рекомбинационным процессом - фиг. 3б. Этим в электрооптических экспериментах обеспечивается режим расширения области пространственного заряда, что характерно для сильного перезахвата электронов ловушками в условиях слабой рекомбинации. При этом tr2-ловушки остаются неактивированными. При дальнейшем повышении температуры рекомбинационные процессы, несмотря на эффективный перезахват, опустошают tr1-центры и обуславливают спад ТСТ и образование низкотемпературного максимума ТСТ. После этого мелкие ловушки tr1 оказываются полностью опустошенными.

При дальнейшем повышении температуры определящую роль играют процессы ионизации электронов с глубоких tr2-ловушек, которые формируют высокотемпературный максимум ТСТ. Однако для этих ловушек, в отличие от tr1, перезахват носителей незначителен - фиг. 3в. Это установлено в электрооптических экспериментах [4], в которых наблюдалось сужение области пространственного заряда в данном температурном интервале.

В соответствии с приведенной физической моделью для описания результатов применяется следующая система кинетических дифференциальных уравнений (1). Она отражает изменение со временем концентрации электронов в зоне проводимости n(t) и степени заполнения электронами ловушек данного типа n_tr(t) при фиксированной температуре Т и начальных условиях n(0)=n₀ и n_tr(0)=n_tr0

где А=1/τ_T - вероятность термической ионизации ловушек, В=1/τ_tr - вероятность захвата свободного электрона ловушкой, С=1/τ_R - вероятность рекомбинации свободных электронов с дырками на R-центрах рекомбинации.

В предельном случае сильного перезахвата носителей, когда рекомбинациоными процессами можно пренебречь, то есть В>>С (τ_R>>τ_tr), система уравнений (1) для начального участка ТСТ-максимума упрощается, сводясь к стационарному случаю, и ее решение имеет вид:

где 1/τ_T=ω_Texp(-E_i/kT).

Формула (2) не применима при сравнительно высоких для этого максимума температурах, когда равновесие нарушается в сторону рекомбинации, поэтому она не описывает максимум ТСТ и его спад.

В другом предельном случае, а именно в случае отсутствия перезахвата и сильной рекомбинации С>>В (τ_R<<τ_tr), система уравнений (1) также упрощается и позволяет (с учетом выражения t=(T-To)/b, b - скорость нагрева) получить выражение для концентрации электронов в зоне проводимости, определяющих величину тока через образец, в виде

В общем случае система (1) также имеет аналитическое решение для n(t) в предположении, что вероятности 1/τ_tr, 1/τ_T, 1/τ_R не зависят от времени.

Фиг. 4 иллюстрирует результат определения E_i по начальным (по Т) участкам двух максимумов ТСТ. Низкотемпературный максимум 1 отвечает случаю сильного перезахвата электронов мелкими ловушками tr1, слабой рекомбинации электронов на R-центрах, то есть случаю заполненных электронами и неактивных при относительно низкой температуре глубоких ловушек tr2. Для низкотемпературного максимума 1 из (2) при логарифмировании получается lnn₁(T)=-E_itr1/kT+ln[τ_tr1ω_Tn_tr1(0)].

Использование координат Аррениуса приводит к линеаризации начального участка. По тангенсу угла наклона линейного участка определяется энергия ионизации мелких ловушек E_i1=0.35 эВ. Высокотемпературный максимум 2 отвечает случаю термической ионизации глубоких ловушек tr2 с последующей рекомбинацией электронов с дырками на R-центрах, отсутствию повторного захвата на tr2-ловушки электронов и полностью термически опустошенных мелких ловушек tr1. Для него на начальном (по Т) участке при логарифмировании получается lnn₂(Т)=-E_i2/kT+ln[τ_Rω_Tn_tr2(0)]. В координатах Аррениуса также определена энергия ионизации ловушек E_i2=0.53 эВ. Указанные методы определения E_i по наклону линеаризованного начального участка ТСТ-максимума согласуются с методами, описанными в работе [7].

Зная уровни «отсечки» на оси ординат lnn₁(T) и lnn₂(T) при 1/kT -> 0, можно оценить соотношение вероятностей 1/τ_T, 1/τ_R захвата электронов мелкими ловушками tr1 и R-центрами рекомбинации: из выражений (2) и (3) следует lnn₁(T)-lnn₂(T)=ln[τ_tr1ω_Tn_tr1(0)]-ln[τ_Rω_Tn_tr2(0)=2.4, откуда τ_tr1/τ_R=3. При этом принималось во внимание отношение степени начального заполнения электронами tr1 и tr2 ловушек предварительной засветкой образца n_tr1(0)/n_tr2(0)=3, что определялось по отношению площадей под максимумами ТСТ 1 и 2. Параметр τ_tr1/τ_R важен для характеристики оптоэлектронных свойств силленитов, так как непосредственно отражает соотношение интегральных способностей примесных центров к захвату носителей.

Таким образом, примененный метод диэлектрической спектроскопии позволяет оценить максвелловское время релаксации высокоомных полупроводниковых кристаллов по результатам измерений частотных зависимостей проводимости, комплексной диэлектрической проницаемости и тангенса угла диэлектрических потерь. Кроме того, при соответствующем выборе частоты регистрации, основанном на информации о частотных спектрах, могут быть определены ключевые параметры примесных центров в кристаллах силленитов. Разработан алгоритм стартовой подготовки образцов, исключающий искажение данных при использовании кристаллов силленитов в качестве датчиков физических величин.

Источники:

1. Osugi Y., Minemoto T. Increase the size of Bil2Si020 real-time hologram for three-dimensional display. Optical Review, Vol. 3, No. 6B (1996), pp. 552-555.

2. М.П. Петров, С.И. Степанов, А.В. Хоменко. Фоторефрактивные кристаллы в когерентной оптике. - С.-Петербург: Наука, 1992. - 320 с.

3. С.М. Рыбкин. Фотоэлектрические явления в полупроводниках. - М.: Физматгиз, 1963. - 496 с.

4. Набиуллина Л.А., Шадрин Е.Б. Магниторезонансные свойства монокристаллов Bi12SiO2O: Fe // Известия РГПУ им. А.И. Герцена. 2012. №147. С. 63-72.

5. Петров М.Р., Степанов С.И., Хоменко А.В. Фоточувствительные электрооптические среды в голографии и оптической обработке информации. Л.: Наука, 1983. 270 с.

6. Ильинский А.В., Кастро Р.А., Набиуллина Л.А., Пашкевич М.Э., Шадрин Е.Б. Магнитооптические эффекты в недопированных кристаллах силиката висмута // Научно-технические ведомости СПбГПУ. Физико-математические науки. 2013. №4-1(182). С. 9-20.

7. Бордовский Г.А., Кастро Р.А. Фотоиндуцированные изменения оптических и контактных свойств халькогенидных стекол // Оптика и спектроскопия. 2001. Т. 90. Вып. 6. С. 884-886.

Диэлектрический метод диагностики электронных состояний в кристаллах силленитов, характеризующий оптоэлектронные свойства силленитов, по результатам измерений частотных зависимостей проводимости, комплексной диэлектрической проницаемости и тангенса угла диэлектрических потерь при разных температурах, отличающийся тем, что образец предварительно нагревался от комнатной температуры до температуры +150°C с целью опустошения ловушек различного типа, присутствующих в кристалле, после чего охлаждался до исходной температуры -70°C, затем освещался в течение 20 минут фотоактивным светом λ=470 нм фиксированной интенсивности и выдерживался в темноте после выключения подсветки в течение 20 минут для исключения возможного влияния на результаты измерений активности сверхмелких ловушек, после этого проводились измерения при медленном 5,2°C/мин нагревании образца от -70°C до +150°C и полученные экспериментальные данные обрабатывались с помощью разработанной математической модели, позволяющей определить значения оптоэлектронных параметров путем сравнения теории с экспериментом.