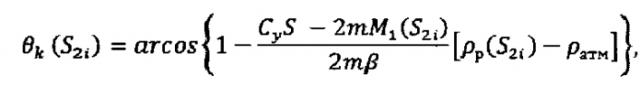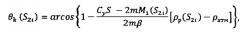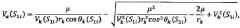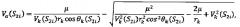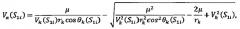Способ управления космическим аппаратом при его выведении на орбиту искусственного спутника планеты

Способ управления космическим аппаратом при его выведении на орбиту искусственного спутника планеты

Иллюстрации

Показать все

Реферат

Изобретение относится к космонавтике, в частности к области выведения космического аппарата (КА) на орбиту искусственного спутника планеты (ИСП) с использованием предварительного аэродинамического торможения в атмосфере.

Известен ряд способов выведения КА на орбиты ИСП. Так, в работе Эйсмонта Н.А. «Оптимальное управление космическим аппаратом, переводимым с гиперболической траектории на орбиту спутника планеты торможением в атмосфере», Космические исследования, 1972, т. 10, вып. 2, стр. 290-292 - [1] описан ракетодинамический способ формирования спутниковых орбит, где осуществляется перевод КА с гиперболической подлетной траектории к планете на орбиту ИСП за счет гашения кинетической энергии КА путем управления двигательными установками большой тяги. Основным недостатком этого способа является чрезвычайно большие затраты топлива.

Способ управления КА при его выведении на орбиту ИСП с использованием предварительного аэродинамического торможения в атмосфере с последующей подачей разгонного импульса в апоцентре переходной орбиты описан в работе - Иванов Н.М., Мартынов А.И. «Управление движением космического аппарата в атмосфере Марса». М.: «Наука», 1977, стр. 357-360 - [2]. Указанный способ заключается в управлении КА на атмосферном участке путем переключения эффективного аэродинамического качества K_эф=K_бcosγ с одного граничного значения на другое (γ - угол крена, K_б - балансировочное аэродинамическое качество, установленное на заданном постоянном угле атаки). Моменты переключений эффективного аэродинамического качества определяются из условия обеспечения максимума скорости КА в апоцентре переходной орбиты. Этот способ позволяет сократить затраты топлива, потребные на формирование заданной орбиты.

Недостатком данного способа является низкая эффективность предварительного аэродинамического торможения в атмосфере планеты в связи с управлением КА только за счет изменения угла крена γ. Вместе с тем, введение дополнительного управляющего параметра - угла атаки α, позволяет уменьшить потребные расходы топлива на формирование заданных орбит ИСП.

В работе Иванова В.М., Соколова Н.Л. и др., «Optimal control of spacecraft during the ascent of Mars artificial satellite». 63nd International Astronautical Congress, Naples, Italy, 2012, № IAC-12,A3,3A,18.p1,x13148 - [3] описан способ выведения КА на орбиту ИСП, где управление аппаратом на участке аэродинамического торможения осуществляется путем совместного изменения углов крена и атаки. Показано наличие выигрыша в массе топлива по сравнению со способом, предусматривающим однопараметрическое управление КА углом крена. При этом была выявлена общая закономерность, характерная для широкого диапазона изменения исходных данных и граничных условий полета. Она заключается в том, что при входе КА в атмосферу вблизи нижней границы коридора расход топлива в несколько раз превосходит расход, соответствующий входу КА в атмосферу на 65-75% коридора входа, отсчитываемого от его верхней границы. Такая особенность позволяет сделать вывод о существенном недостатке рассматриваемого способа, заключающемся в значительном перерасходе массы топлива в случаях входа КА в атмосферу вблизи нижней границы коридора и существовании резервов для снижения потребных энергозатрат.

Наиболее близким по совокупности существующих признаков и достигаемому результату (прототипом) к заявленному изобретению является способ перевода космического аппарата на орбиту ИСП, предусматривающий подачу импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты, при входе КА в атмосферу вблизи нижней границы коридора, а также управление аэродинамическими силами на участке движения в атмосфере с последующим разгоном космического аппарата в апогее переходной орбиты. Указанный известный способ описан в книге - Иванов Н.М., Мартынов А.И. «Движение космических летательных аппаратов в атмосферах планет». М.: «Наука», 1985, стр. 347-364 - [4]. За счет движения КА в более разреженных слоях атмосферы, осуществляемого после проведения коррекции траектории полета, скорость КА гасится слабее и обеспечивается уменьшение расхода топлива на формирование конечных орбит. В рамках данного способа предполагается, что основным признаком движения КА вблизи нижней границы коридора входа является высокая интенсивность возрастания кажущейся скорости после входа космического аппарата в атмосферу. В этом случае подается импульс характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты, через 20-40 секунд после входа КА в атмосферу. Показано, что теоретически такой способ управления при проведении оптимальных коррекций траекторий движения КА при его входе в атмосферу вблизи нижней границы коридора входа позволяет обеспечить снижение массы топлива в 1,5-2 раза по сравнению со способом, не предусматривающим подачу корректирующего импульса в атмосфере.

Вместе с тем, анализ операций управления КА при реализации данного способа позволяет выявить ряд недостатков. Во-первых, высокая интенсивность роста кажущейся скорости может быть не только признаком движения КА вблизи нижней границы коридора входа, но и возникать в связи с возможным разбросом плотности атмосферы планет в сторону наиболее плотных моделей атмосферы. Так, например, плотности атмосферы Юпитера для «холодной» и «теплой» моделей отличаются на 2-3 порядка [4, стр. 23]. Ошибки в диагностировании причин интенсивного роста кажущейся скорости могут привести к принятию некорректного решения о необходимости проведения коррекций движения КА в атмосфере: подача импульса характеристической скорости в большей части коридора входа (65-75% от общей ширины коридора) может привести к дополнительному перерасходу топлива, а при движении КА вблизи верхней границы коридора - к невозможности выведения КА на заданную орбиту и к срыву программы полета. Во-вторых, в способе-прототипе предполагается проведение коррекций траекторий движения через 20-40 секунд после входа КА в атмосферу, например, при входе в атмосферу Юпитера через 21 секунду. Несмотря на то, что за это время скорость движения КА меняется мало, высота полета снижается примерно в два раза. В результате КА подвергается избыточному аэродинамическому торможению и, как следствие, к снижению скорости вылета аппарата из атмосферы. Вместе с тем, за указанное время (20-40 секунд после входа КА в атмосферу) может быть успешно решена задача автономного определения положения КА внутри коридора входа в атмосферу за счет использования бортовых алгоритмов прогнозирования параметров движения аппарата на оставшихся участках и обоснована необходимость (или ее отсутствие) проведения коррекции движения КА. В третьих, в способе-прототипе предусматривается подача импульса характеристической скорости, величина которого не зависит от высоты условного перицентра траектории входа. Вместе с тем, характер зависимости потребных энергозатрат ΔV от высоты условного перецентра траектории входа показывает чрезвычайно интенсивный рост ΔV при приближении h_π к нижней границе коридора . Это обстоятельство дает основание предполагать, что значительным резервом снижения суммарных затрат топлива на формирование спутниковых орбит является выбор и отработка рациональных значений корректирующих импульсов характеристической скорости, зависящих от высот условного перицентра траекторий входа. При этом в ряде случаев представляется энергетически эффективным последовательно подавать в атмосфере несколько корректирующих импульсов характеристической скорости различной величины.

Сущность изобретения заключается в предварительном определении положения высоты условного перицентра траектории входа космического аппарата в атмосферу внутри заданного физически реализуемого коридора. Это достигается путем определения сразу после входа космического аппарата в атмосферу в i-е (i=1, 2, 3…) моменты времени значений скорости движения космического аппарата V_i, угла наклона вектора скорости к местному горизонту θ_i, радиуса-вектора r_i, плотности атмосферы ρ_i и прогнозирования на их основе значений скоростей V_k и углов наклона вектора скорости к местному горизонту θ_k на момент вылета космического аппарата из атмосферы, а также его скоростей в апоцентре переходной орбиты V_α при движении на участке аэродинамического торможения с нулевым углом крена и углом атаки α^*, соответствующим максимальному значению аэродинамического качества.

Также сущность заявленного способа управления космическим аппаратом при его выведении на орбиту искусственного спутника планеты заключается в подлете космического аппарата к планете в заданном коридоре входа в атмосферу, в определении в i-е, где i=1, 2,…, N, моменты времени параметров движения космического аппарата, а именно его скорости - V_i, угла наклона вектора скорости космического аппарата к местному горизонту θ_i, радиуса-вектора r_i и плотности атмосферы ρ_i, в обеспечении входа космического аппарата в атмосферу с величиной угла крена γ около 0 рад и значением угла атаки космического аппарата около α^*, соответствующим максимальной величине аэродинамического качества, в подаче импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты, при его входе в атмосферу вблизи нижней границы коридора входа, в управлении космическим аппаратом по углам крена γ и атаки α до вылета из атмосферы, при этом в i-е, где i=1, 2,…, N, моменты времени для заданного положительного приращения угла наклона вектора скорости к местному горизонту δθ≤0,1° определяют значения импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты, приложение которого обеспечивает увеличение угла θ_i на величину δθ; для каждого из двух положений космического аппарата, характеризующихся известными значениями параметров его движения S_1i={V_i, θ_i, r_i, ρ_i} и S_2i={V_i, θ_i+δθ, r_i, ρ_i} прогнозируют значения скоростей V_к(S_1i) и V_к(S_2i), углов наклона вектора скорости к местному горизонту θ_к(S_1i) и θ_к(S_2i) на момент вылета космического аппарата из атмосферы и скоростей космического аппарата в апоцентре переходной орбиты V_α(S_1i) и V_α(S_2i) при движении на оставшихся участках полета в атмосфере с нулевым углом крена и углом атаки, равным α^* в соответствии с математическими зависимостями:

V_k(S_1i)=exp[-z_k(S_1i )], V_k(S_2i)=exp[-z_k(S_2i)],

где - m - масса космического аппарата;

V_i - текущее значение скорости космического аппарата в моменты времени t_i

θ_i - текущее значение угла наклона вектора скорости к местному горизонту в моменты t_i;

r_i - текущее значение радиуса-вектора в момент времени t_i;

ρ_i - текущее значение плотности атмосферы в моменты времени t_i

i=0, 1, 2…N;

g - ускорение свободного падения;

R - радиус планеты;

µ - гравитационный параметр планеты;

β - логарифмический коэффициент изменения плотности атмосферы от высоты;

C_x - аэродинамический коэффициент лобового сопротивления космического аппарата;

С_γ - аэродинамический коэффициент подъемной силы космического аппарата;

S - площадь миделева сечения космического аппарата;

α - угол атаки космического аппарата;

ρ_p - значение плотности атмосферы в момент рикошета космического аппарата;

z_p - значение переменной z в момент рикошета космического аппарата;

S_1i - положение космического аппарата в момент времени t_i,

характеризующееся скоростью полета V_i, углом наклона вектора скорости к местному горизонту θ_i, радиусом-вектором r_i, плотностью атмосферы ρ_i;

S_2i - положение космического аппарата в момент времени t_i,

характеризующееся скоростью полета V_i, углом наклона вектора скорости к местному горизонту θ_i+δθ, радиусом-вектором r_i, плотностью атмосферы ρ_i;

δθ - приращение угла наклона вектора скорости к местному горизонту, образующееся при подаче корректирующего импульса характеристической скорости;

P_x - приведенная нагрузка на лобовую поверхность космического аппарата;

K - аэродинамическое качество космического аппарата;

V_k - скорость полета космического аппарата в момент вылета из атмосферы;

r_k - радиус-вектор космического аппарата в момент вылета из атмосферы;

θ_k - угол наклона вектора скорости к местному горизонту в момент вылета космического аппарата из атмосферы;

V_α - скорость космического аппарата в апоцентре переходной орбиты,

вычисляют разницу между изменением скорости космического аппарата в апоцентре переходной орбиты и величиной импульса характеристической скорости, обеспечивающего увеличение угла наклона вектора скорости к местному горизонту на величину δθ в соответствии с формулой

δV_i=V_α(S_2i)-V_α(S_1i)-ΔV_i,

и при выполнении условия δV_i>0 подают импульс характеристической скорости величиной ΔV_i; начиная с момента времени, когда величина δV_i будет меньше нуля, осуществляют управление космическим аппаратом без проведения ракетодинамических коррекций траекторий движения до вылета космического аппарата из атмосферы только путем изменения углов крена и атаки.

Учитывая характер зависимостей потребных энергетических затрат ΔV от высоты условного перицентра траектории входа h_π (см. рис. 10.2 на стр. 289 и рис. 10.12 на стр. 314 в работе [4]) и давая малые приращения углу наклона вектора скорости к местному горизонту δθ≤0,1° (что согласно решению кеплеровских уравнений однозначно соответствует приращению высоты условного перицентра δh_π,), можно определить положение высоты h_π внутри коридора входа космического аппарата в атмосферу. Принципиальным фактором является сравнение скоростей движения аппарата в апоцентре переходной орбиты V_α при двух положениях КА на начальном участке полета в атмосфере: при положении, обозначенном S_1i и характеризующимся известными параметрами движения (скоростью аппарата V_i, углом наклона вектора скорости к местному горизонту θ_i, радиусом-вектором r_i и плотностью атмосферы ρ_i) и при положении, обозначенном S_2i, отличающимся от положения S_1i значением угла наклона вектора скорости к местному горизонту, увеличенным на малую величину δθ≤0,1°:θ=θ_i+δθ. Малое изменение скорости V_α(S_2i)относительно V_α(S_1i) при приращении δθ (или δh_π) свидетельствует о входе аппарата в атмосферу с высотами h_π, значительно удаленными от нижней границы коридора входа : в этих случаях проводить коррекцию движения космического аппарата не требуется. В случаях значительного увеличения скорости V_α(S_2i) по сравнению с V_α(S_1i) (или снижения потребных энергетических затрат ΔV) при положительной вариации угла δθ (или δh_π) следует вывод о входе космического аппарата в атмосферу вблизи нижней границы коридора и энергетической целесообразности проведения ракетодинамической коррекции траектории движения для обеспечения полета космического аппарата в более разреженных слоях атмосферы.

Для расчета значений скорости V_k и угла наклона вектора скорости к местному горизонту θ_k на момент вылета КА из атмосферы, соответствующих положениям S_1i и S_2i, a также скоростей КА в апоцентре переходной орбиты V_α(S_1i) и V_α(S_2i) использовались математические зависимости, разработанные, обоснованные и приведенные в приложении к данной заявке:

V_k(S_1i)=exp[-z_k(S_1i)], V_k(S_2i)=exp[-z_k(S_2i)],

где m - масса космического аппарата;

V_i - текущее значение скорости космического аппарата в моменты t_i;

θ_i - текущее значение угла наклона вектора скорости КА к местному горизонту в моменты t_i;

r_i - текущее значение радиуса-вектора в момент t_i;

ρ_i - текущее значение плотности атмосферы моменты t_i, i=0, 1, 2…N;

g - ускорение свободного падения;

R - радиус планеты;

µ - гравитационный параметр планеты;

β - логарифмический коэффициент изменения плотности атмосферы от высоты;

C_x - аэродинамический коэффициент лобового сопротивления КА;

С_γ - аэродинамический коэффициент подъемной силы КА;

S - площадь миделева сечения КА;

α - угол атаки космического аппарата;

ρ_p - значение плотности атмосферы в момент рикошета космического аппарата;

z_p - значение переменной z в момент рикошета космического аппарата;

S_1i - положение космического аппарата в момент времени t_i, характеризующееся скоростью полета V_i, углом наклона вектора скорости к местному горизонту θ_i, радиусом-вектором r_i, плотностью атмосферы ρ_i;

S_2i - положение космического аппарата в момент времени t_i, характеризующееся скоростью полета V_t, углом наклона вектора скорости к местному горизонту θ_i+δθ, радиусом-вектором r_i, плотностью атмосферы ρ_i;

δθ - приращение угла наклона вектора скорости КА к местному горизонту, образующееся при подаче корректирующего импульса характеристической скорости;

P_x - приведенная нагрузка на лобовую поверхность космического аппарата;

K - аэродинамическое качество КА;

V_k - скорость полета космического аппарата в момент вылета из атмосферы;

r_k - радиус-вектор космического аппарата в момент вылета из атмосферы;

θ_k - угол наклона вектора скорости КА к местному горизонту в момент вылета космического аппарата из атмосферы;

V_α - скорость космического аппарата в апоцентре переходной орбиты.

Прогнозирование указанных значений может осуществляться на бортовой вычислительной машине с помощью аналитических зависимостей, что не требует больших временных затрат и может быть проведено значительно раньше указанного в способе-прототипе временного диапазона определения высоты условного перицентра траектории входа (20-40 сек после входа космического аппарата в атмосферу). При условии выявления целесообразности проведения ракетодинамической коррекции траектории движения космического аппарата в атмосфере определяется величина подаваемого импульса характеристической скорости. Для этого в i-е (i=1, 2, 3…) моменты времени сравнивают возможное увеличение скорости КА в апоцентре переходной орбиты при проведении ракетодинамической коррекции траектории движения ΔV_α=V_α(S_2i)-V_α(S_1i) с величиной

подаваемого корректирующего импульса, зависящего от текущей скорости космического аппарата V_i и приращения угла наклона вектора скорости к местному горизонту δθ: . В случаях превышения разницы между скоростями движения КА в апоцентре переходной орбиты при условиях проведения и непроведения коррекции над величиной импульса характеристической скорости ΔV_i, т.е. при δV_i=V_α(S_2i)-V_α(S_1i)-ΔV_i>0 осуществляется подача корректирующего импульса ΔV_i в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты. Такие операции осуществляются с самого начала входа космического аппарата в атмосферу до тех пор, пока величина импульса характеристической скорости ΔV_i не будет превышать прогнозируемый выигрыш в потребных энергозатратах на подачу разгонного импульса характеристической скорости в апоцентре переходной орбиты, т.е. до тех пор, пока значение δV_i не будет меньше нуля. С этого момента осуществляется управление только аэродинамическими силами, по аналогии с известными способами управления [3, 4]. Полученные численные результаты показали, что при осуществлении заявляемого способа в зависимости от высоты условного перицентра траектории входа может быть проведено до трех ракетодинамических коррекций траекторий движения КА. При этом общее время проведения коррекций может достигать 8-12 секунд. Такие результаты соответствуют входу космического аппарата в атмосферу по нижней границе коридора. В целом при реализации заявляемого способа при формировании орбит искусственного спутника Марса потребная масса топлива может быть снижена в 2-3 раза по сравнению со способом - прототипом. Аналогичный уровень снижения расхода топлива может быть достигнут при выведении КА на орбиты искусственного спутника Венеры и Юпитера.

Технический результат изобретения заключается в повышении эффективности управления КА на участке предварительного аэродинамического торможения не только за счет изменения углов крена γ и атаки α, но и в связи с проведением ракетодинамических коррекций траекторий движения КА. Это позволит при входе КА в атмосферу вблизи нижней границы коридора входа осуществить полет в более разреженных слоях атмосферы и достигнуть заданных высот апоцентра переходной орбиты с большей скоростью, что обеспечивает снижение суммарного расхода топлива на формирование орбит ИСП с требуемыми параметрами.

Указанный технический результат достигается за счет автономного оперативного определения бортовыми средствами КА высоты условного перицентра сразу после входа КА в атмосферу и проведения ракетодинамической коррекции траектории при входе космического аппарата в атмосферу вблизи нижней границы коридора входа. При этом отрабатываются рациональные программы управления аэродинамическими силами до вылета КА из атмосферы и проводится разгон аппарата в апоцентре переходной орбиты с целью формирования орбиты ИСП с заданными параметрами.

Также технический результат достигается за счет того, что в известном способе- прототипе управления космическим аппаратом, при его выведении на орбиту искусственного спутника планеты, заключающимся в подлете космического аппарата к планете в заданном коридоре входа в атмосферу, в определении в i-е, где i=1, 2,…, N, моменты времени параметров движения космического аппарата, а именно его скорости - V_i, угла наклона вектора скорости космического аппарата к местному горизонту θ_i, радиуса-вектора r_i и плотности атмосферы ρ_i, в обеспечении входа космического аппарата в атмосферу с величиной угла крена γ около 0 рад и значением угла атаки космического аппарата около α^*, соответствующим максимальной величине аэродинамического качества, в подаче импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты, при его входе в атмосферу вблизи нижней границы коридора входа, в управлении космическим аппаратом по углам крена γ и атаки α до вылета из атмосферы, дополнительно в i-е, где i=1, 2,…, N, моменты времени для заданного положительного приращения угла наклона вектора скорости к местному горизонту δθ≤0,1° определяют значения импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против часовой стрелки в направлении от планеты, приложение которого обеспечивает увеличение угла θ_i на величину δθ; для каждого из двух положений космического аппарата, характеризующихся известными значениями параметров его движения S_1i=[V_i, θ_i, r_i, ρ_i} и S_2i={V_i, θ_i+δθ, r_i, ρ_i} прогнозируют значения скоростей V_к(S_1i) и V_к(S_2i), углов наклона вектора скорости к местному горизонту θ_к(S_1i) и θ_к(S_2i) на момент вылета космического аппарата из атмосферы и скоростей космического аппарата в апоцентре переходной орбиты V_α(S_1i) и V_α(S_2i) при движении на оставшихся участках полета в атмосфере с нулевым углом крена и углом атаки, равным α^* в соответствии с математическими зависимостями:

V_k(S_1i)=exp[-z_k(S_1i)], V_k(S_2i)=exp[-z_k(S_2i)],

где - m - масса космического аппарата;

V_i - текущее значение скорости космического аппарата в моменты времени t_i

θ_i - текущее значение угла наклона вектора скорости к местному горизонту в моменты t_i;

r_i - текущее значение радиуса-вектора в момент времени t_i;

ρ_i - текущее значение плотности атмосферы в моменты времени t_i;

i=0, 1, 2…N;

g - ускорение свободного падения;

R - радиус планеты;

µ - гравитационный параметр планеты;

β - логарифмический коэффициент изменения плотности атмосферы от высоты;

C_x - аэродинамический коэффициент лобового сопротивления космического аппарата;

C_γ - аэродинамический коэффициент подъемной силы космического аппарата;

S - площадь миделева сечения космического аппарата;

α - угол атаки космического аппарата;

ρ_p - значение плотности атмосферы в момент рикошета космического аппарата;

z_p - значение переменной z в момент рикошета космического аппарата;

S_1i - положение космического аппарата в момент времени t_i, характеризующееся скоростью полета V_i, углом наклона вектора скорости к местному горизонту θ_i, радиусом-вектором r_i, плотностью атмосферы ρ_i;

S_2i - положение космического аппарата в момент времени t_i, характеризующееся скоростью полета V_i, углом наклона вектора скорости к местному горизонту θ_i+δθ, радиусом-вектором r_i, плотностью атмосферы ρ_i;

δθ - приращение угла наклона вектора скорости к местному горизонту, образующееся при подаче корректирующего импульса характеристической скорости;

P_x - приведенная нагрузка на лобовую поверхность космического аппарата;

K - аэродинамическое качество космического аппарата;

V_k - скорость полета космического аппарата в момент вылета из атмосферы;

r_k - радиус-вектор космического аппарата в момент вылета из атмосферы;

θ_k - угол наклона вектора скорости к местному горизонту в момент вылета космического аппарата из атмосферы;

V_α - скорость космического аппарата в апоцентре переходной орбиты, вычисляют разницу между изменением скорости космического аппарата в апоцентре переходной орбиты и величиной импульса характеристической скорости, обеспечивающего увеличение угла наклона вектора скорости к местному горизонту на величину δθ в соответствии с формулой:

δV_i=V_α(S_2i)-V_α(S_1i)-ΔV_i,

и при выполнении условия δV_i>0 подают импульс характеристической скорости величиной ΔV_i, начиная с момента времени, когда величина δV_i будет меньше нуля, осуществляют управление космическим аппаратом без проведения ракетодинамических коррекций траекторий движения до вылета космического аппарата из атмосферы только путем изменения углов крена и атаки.

Заявленный способ управления космическим аппаратом при его выведении на орбиту искусственного спутника планеты поясняется следующими фигурами.

На фиг. 1 приведены основные этапы выведения КА на орбиту искусственного спутника планеты с использованием предварительного аэродинамического торможения, как с применением, так и при отсутствии ракетодинамической коррекции траектории движения аппарата в атмосфере.

На фиг. 2 для заявленного способа приведены графики зависимостей суммарных энергозатрат ΔV_Σ, от высоты условного перицентра траектории входа h_π при выведении КА на круговую орбиту искусственного спутника Марса, высотой 500 км. Значения h_π варьировались в пределах от верхней границы коридора входа до нижней границе .

На фиг. 1 и фиг. 2 приняты следующие обозначения:

1 - подлетная гиперболическая траектория КА к атмосфере планеты,

2 - вход КА в атмосферу,

3 - подача импульса характеристической скорости ΔV для проведения коррекции траектории движения КА,

4 - вектор скорости КА после проведения коррекции траектории движения,

5 - траектория полета КА без проведения ракетодинамической коррекции;

6 - траектория полета КА после проведения ракетодинамической коррекции,

7 - вылет КА из атмосферы по траектории без проведения ракетодинамической коррекции со скоростью V_α(S₂),

8 - вылет КА из атмосферы по траектории после проведения ракетодинамической коррекции со скоростью V_α(S₁),

9 - переходная орбита КА при отсутствии коррекции движения в атмосфере;

10 - переходная орбита КА после проведения коррекции движения в атмосфере,

11 - апоцентр переходной орбиты КА,

12 - подача импульса характеристической скорости для формирования заданной орбиты КА,

13 - поверхность планеты,

14 - условная граница атмосферы,

15 - зависимость суммарных энергозатрат ΔV_Σ от высоты условного перицентра траектории входа h_π при отсутствии проведения ракетодинамической коррекции движения КА в атмосфере,

16 - зависимость суммарных энергозатрат ΔV_Σ от высоты условного перицентра траектории входа h_π при подаче в атмосфере импульса характеристической скорости величиной 25 м/с,

17 - зависимость суммарных энергозатрат ΔV_Σ от высоты условного перицентра траектории входа h_π при подаче в атмосфере импульса характеристической скорости величиной 50 м/с.

Из зависимостей, представленных на фиг. 2, следует, что для варианта с проведением коррекции движения КА в атмосфере траектория полета проходит на больших высотах, что приводит к менее интенсивному аэродинамическому торможению аппарата и большему значению скорости вылета КА из атмосферы: V_α(S₂) - скорость КА при вылете из атмосферы при использовании схемы с проведением коррекции траектории полета, V_α(S₁) - скорость КА при вылете из атмосферы без проведения ракетодинамической коррекции. Установлено, что V_α(S₂)-V_α(S₁)-ΔV>0, т.е. имеет место выигрыш в потребных энергетических затратах при осуществлении коррекции движения КА в атмосфере.

Способ управления космическим аппаратом при его выведении на орбиту искусственного спутника планеты, заключающийся в подлете космического аппарата к планете в заданном коридоре входа в атмосферу, в определении в i-е, где i=1, 2, …, N, моменты времени параметров движения космического аппарата, а именно его скорости V_i, угла наклона вектора скорости космического аппарата к местному горизонту θ_i, радиуса-вектора r_i и плотности атмосферы ρ_i, в обеспечении входа космического аппарата в атмосферу с величиной угла крена γ около 0 и значением угла атаки космического аппарата около α^*, соответствующим максимальной величине аэродинамического качества, в подаче импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против хода часовой стрелки в направлении от планеты, при его входе в атмосферу вблизи нижней границы коридора входа, в управлении космическим аппаратом по углам крена γ и атаки α до вылета из атмосферы, отличающийся тем, что в i-е, где i=1, 2,…, N, моменты времени для заданного положительного приращения угла наклона вектора скорости к местному горизонту δθ ≤ 0,1° определяют значения импульса характеристической скорости в плоскости полета космического аппарата под углом около 90°, отсчитываемым от вектора скорости космического аппарата против хода часовой стрелки в направлении от планеты, приложение которого обеспечивает увеличение угла θ_i на величину δθ, для каждого из двух положений космического аппарата, характеризующихся известными значениями параметров его движения S_1i={V_i, θ_i, r_i, ρ_i} и S_2i={V_i, θ_i+δθ, r_i, ρ_i}, прогнозируют значения скоростей V_к(S_1i) и V_к(S_2i), углов наклона вектора скорости к местному горизонту θ_к(S_1i) и θ_к(S_2i) на момент вылета космического аппарата из атмосферы и скоростей космического аппарата в апоцентре переходной орбиты V_α(S_1i) и V_α(S_2i) при движении на оставшихся участках полета в атмосфере с нулевым углом крена и углом атаки, равным α^*, вычисляют разницу между изменением скорости космического аппарата в апоцентре переходной орбиты и величиной импульса характеристической скорости, обеспечивающего увеличение угла наклона вектора скорости к местному горизонту на величину δθ в соответствии с формулой:δV_i=V_α(S_2i)-V_α(S_1i)-ΔV_i,и при выполнении условия δV_i > 0 подают импульс характеристической скорости величиной ΔV_i, начиная с момента времени, когда величина δV_i будет меньше нуля, осуществляют управление космическим аппаратом без проведения ракетодинамических коррекций траекторий движения до вылета космического аппарата из атмосферы только путем изменения углов крена и атаки.