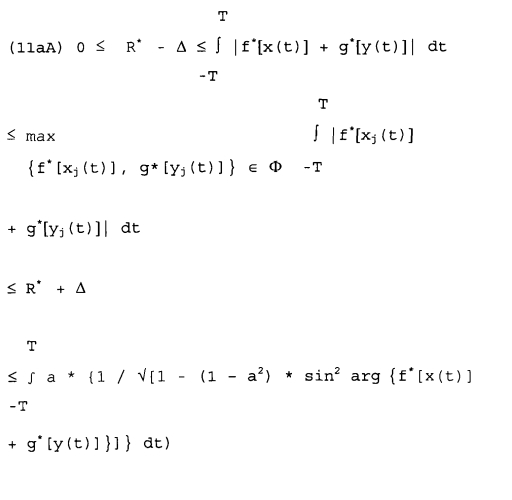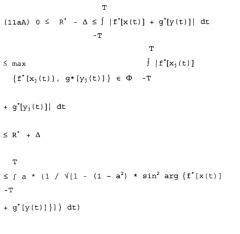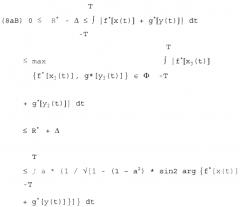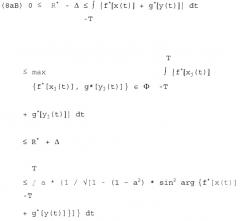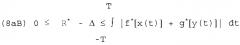Устройство и способ оценки и оптимизации сигналов на основе алгебраических инвариантов

Устройство и способ оценки и оптимизации сигналов на основе алгебраических инвариантов

Иллюстрации

Показать все

Реферат

Изобретение относится к сигналам (например, аудиосигналам) и устройствам или способам для их генерирования, передачи, оценки, преобразования и воспроизведения.

Настоящее изобретение относится, в частности, к способу и устройству или системе для осуществления оценки на основе любого отображения или любых отображений одного или нескольких сигналов или также связи или связей двух или нескольких сигналов. Для того чтобы делать выводы относительно свойств сигналов, в случае стереофонического сигнала x(t), y(t), причем x(t) представляет собой функциональное значение левого входного сигнала в момент времени t, y(t) представляет собой функциональное значение правого входного сигнала в момент времени t, можно, например, рассматривать сумму передаточных функций

f * [ x ( t ) ] = [ x ( t ) / 2 ] * ( − 1 + i ) g * [ y ( t ) ] = [ y ( t ) / 2 ] * ( 1 + i )

Эта оценка должна, в частности, осуществляться применительно к общим свойствам двух различных сигналов, которые полностью соответствуют случайному принципу (как, например, аудиосигналы).

Известные методы пытались смоделировать этот случайный принцип - с соответственно большими трудностями - и применять, таким образом, для рассматриваемых сигналов. Так в случае DAB (Digital Audio Broadcasting - цифровое аудиовещание) моделируется гауссов процесс с так называемой моделью многоотводной линии задержки (Tapped Delay Line Modell), или для моделирования мобильного радиоканала применяется метод Монте-Карло (окрашенный комплексный гауссов шум в двух размерностях).

В ЕР 0825800 (Thomson Brandt GmbH) предложено формирование различных сигналов из входного моносигнала путем фильтрации, из которых - например, с помощью способа, предложенного Лауридсеном, на основе коррекции по амплитуде и по времени прихода, в зависимости от ситуации приема - отдельно генерируются виртуальные однополосные стереосигналы, которые затем комбинируются в два выходных сигнала.

В WO 2009/138205 или ЕР 2124486, а также ЕР 1850639 описан, например, способ методической оценки угла падения для отображаемого звукового события, образованного главной осью микрофона и осью пеленга на источник звука, при применении фазовых разностей и амплитудных коррекций, которые являются функционально зависимыми от первоначальной ситуации приема (которую можно интерполировать на основе системы). Содержание WO 2009/138205 или ЕР 2124486, а также ЕР 1850639 настоящим включено в данную заявку посредством ссылки.

В US 5173944 (Begault Durand) HRTF (передаточные функции слухового аппарата человека), которые коррелируют по азимуту 90, 120, 240 и 270 градусов, применяются по отношению к соответственно различным образом задержанным, однако единым образом усиленным монофоническим входным сигналам, причем образованные сигналы затем вновь накладываются на первоначальный моносигнал. Амплитудная коррекция, а также коррекция времени прихода выбираются при этом независимо от ситуации приема.

В СН 01159/09 или соответственно РСТ/ЕР2010/055876 раскрывается подключение одного или нескольких панорамных потенциометров или эквивалентных вспомогательных средств в устройстве согласно WO 2009/138205, или соответственно ЕР 2124486, или ЕР 1850639, после осуществленного стереофонического преобразования, (после выполненного прохождения через MS-матрицу, для которой справедливо соотношение

L = ( M + S ) * 1 / 2

и

R = ( M − S ) * 1 / 2 ),

которые не приводят, как в случае и сигналов при интенсивностной стерефонии, то есть в случае стереофонических сигналов, которые отличаются исключительно своим уровнем, но не разностью времени прихода или соответственно фаз или разными частотными спектрами, к ограничению ширины отображения или сдвигу направления отображения полученных стереосигналов, а скорее приводит к повышению или снижению степени корреляции.

СН 01776/09 или РСТ/ЕР2010/055877 позволяют осуществить оптимальный выбор тех параметров, которые лежат в основе генерирования стереофонических или псевдостереофонических сигналов. Пользователю предоставляются средства, чтобы устанавливать степень корреляции, область определения, громкость, а также другие параметры результирующих сигналов согласно психоакустическим аспектам и тем самым устранять артефакты.

В целом, в отношении уровня техники можно сказать, что до сих пор в результате отсутствия соответствующих основ

алгебраические инварианты ранее не применялись для анализа или оптимизации звуковых событий или подобных процессов.

Хотя со времени новаторских работ Дэвида Гильберта, относящихся к алгебраическим инвариантам, уже более 100 лет в принципе высказываются предположения, что подобные алгебраические инварианты, в частности для гауссовых процессов, существуют, доказать это до сих пор не удавалось.

Сущность изобретения

Предложенное изобретение не только доказывает такие алгебраические инварианты, но и делает их практически применимыми для сигнальной техники, например, для калибровки устройств или способов получения, улучшения или оптимизации стереофонических или псевдостереофонических аудиосигналов.

Сначала рассматривается связь f^(t) или несколько связей f₁^(t), f₂^(t),…, f_p^(t) по меньшей мере двух сигналов s₁(t), s₂(t),…, s_m(t) или их передаточных функций t₁(s₁(t)), t₂(s₂(t)),…, t_m(s_m(t)) - или также произвольно определяемое отображение f^#(t) или произвольно определяемые отображения f₁ ^#(t), f₂ ^#(t),…, f_µ ^#(t) сигнала s^#(t) или нескольких сигналов s₁ ^#(t), s₂ ^#(t),…, s_Ω ^#(t) на комплексной числовой плоскости или ее проекции на рельеф, который определен посредством нормы всех точек комплексной числовой плоскости (стандартный конус, вершина которого лежит в начале координат комплексной числовой плоскости, и оси симметрии которого лежат перпендикулярно комплексной числовой плоскости).

Действительная ось, мнимая ось и ось симметрии конуса воспринимаются как прямоугольная система координат с координатами (х₁, х₂, х₃). Изменение угла раскрыва конуса приводит к уравнению конуса:

x₁ ²+x₂ ²-(1/g*²)*x₃=0

или коэффициентам [1 1 -1/g*²]. Если теперь рассмотреть два уравнения конуса

S:=a_x ²:=1*x₁ ²+1*x₂ ²-(1/g²)*x₃ ²=0

и

S':=a'_x ²:=1*x₁ ²+1*x₂ ²-(1/g'²)*x₃ ²=0.

Инвариант, таким образом, как известно:

a_a' ²:=1*1²+1*1²-(1/g²)*(1/g'⁴).

Оба конуса S, S' являются неполярными, если действительно уравнение:

(1/g²)*(1/g'⁴)=2.

Тогда S записывается в S' гармонически.

Рассмотрим теперь вышеупомянутую связь f^(t) или несколько связей f₁^(t), f₂^(t),…, f_p^(t) двух или нескольких сигналов s₁(t), s₂(t),…, s_m(t) или их передаточных функций t₁(s₁(t)), t₂(s₂(t)),…, t_m(s_m(t)) для двух временных отрезков t₁, t₂ - или также произвольно определяемое отображение f^#(t) или произвольно определяемые отображения f₁ ^#(t), f₂ ^#(t),…, f_µ ^#(t) сигнала s^#(t) или нескольких сигналов s₁ ^#(t), s₂ ^#(t),…, s_Ω ^#(t) для двух временных отрезков t₁, t₂ - а также отображения S, S' и Σ' с

Σ':=u_a' ²:=A'u₁ ²+B'u₂ ²+C'u₃ ²+2F'u₂u₃ +2G'u₃u₁+2H'u₁u₂

=1*u₁ ²+1*u₂ ²+(1/g''²)*u₃ ²+2*1*u₂u₃+2*1*u₃u₁+2*1*u₁u₂=0.

Должно быть действительным уравнение

aA'+bB'+cC'+2fF'+2gG'+2hH'=0

и S и Σ' должны быть неполярными:

1*1+1*1-(1/g²)*(1/g''²)=0

или

(1/g²)*(1/g''²)=2.

Таким образом, если справедливо g'=g''=1 и g=1/√2, то обеспечивается неполярность S c S' и Σ'.

Рассмотрение стандартного конуса

S'=1*x₁ ²+1*x₂ ²-1*x₃ ²=0 допускает, таким образом, рассмотрение идентичных обращающихся в нуль инвариантов относительно S:

S=1*x₁ ²+1*x₂ ²-2*x₃ ²=0

или соответственно

Σ'=1*u₁ ²+1*u₂ ²+1*u₃ ²+2*1*u₂u₃+2*1*u₃u₁+2*1*u₁u₂=0.

Тем самым соотношение

a_a' ²:=1*1²+1*1²-2*1²=0

линейно в коэффициентах уравнений

S=1*x₁ ²+1*x₂ ²-2*x₃ ²=0

и

Σ'=1*u₁ ²+1*u₂ ²+1*u₃ ²+2*1*u₂u₃+2*1*u₃u₁+2*1*u₁u₂=0.

Согласно известному положению Гильберта об инвариантных телах (Hilbert, стр.291, пар. 2), в нашей системе линейная комбинация

ϕ [1, 1, -2]*[1, 1, -1]²+

Θ [1, 1, -2]*[1, 1, 1]²=0

вновь представляет собой инвариант. Тем самым соответствуют, например, любые рассматриваемые на плоскости, проходящей через векторы (1, 1, -2) и (1, 1, 1), пересекающиеся прямые f^(t₁) и f^(t₂), ξ₁ и ξ₂ бесконечно многим инвариантам S и S' или соответственно S и Σ'.

При рассмотрении стандартного конуса, отображенного на комплексной числовой плоскости изменение угла раскрыва конуса, приводит к уравнению конуса

-x₁ ²-x₂ ²+(1/g*²)*x₃

или к коэффициентам [-1 -1 1/g*²]. Теперь рассмотрим два уравнения конуса

S:=a_x ²:=-1*x₁ ²-1*x₂ ²+(1/g*²)*x₃ ²=0

и

S':=a'_x ²:=-1*x₁ ²-1*x₂ ²+(1/g'*²)*x₃ ²=0.

Инвариант, таким образом, как известно:

a_a' ²:=-1*(-1)²-1*(-1)²+(1/g²)*(1/g'⁴).

Оба конуса S, S', являются неполярными, если справедливо

(1/g²)*(1/g'⁴)=2.

Тогда S записывается в S' гармонически.

Рассмотрим теперь, например, вышеупомянутую связь f^(t) или несколько связей f₁^(t), f₂^(t),…, f_p^(t) двух или нескольких сигналов s₁(t), s₂(t),…, s_m(t) или их передаточных функций t₁(s₁(t)), t₂(s₂(t)),…, t_m(s_m(t)) для двух временных отрезков t₁, t₂ - или также произвольно определяемое отображение f^#(t) или произвольно определяемые отображения f₁ ^#(t), f₂ ^#(t),…, f_µ ^#(t) сигнала s^#(t) или нескольких сигналов s₁ ^#(t), s₂ ^#(t),…, s_Ω ^#(t) для двух временных отрезков t₁, t₂ - а также отображения S, S' и Σ' с

Σ':=u_a' ²:=A'u₁ ²+B'u₂ ²+C'u₃ ²+2F'u₂u₃ +2G'u₃u₁+2H'u₁u₂

=1*u₁ ²+1*u₂ ²+(1/g''²)*u₃ ²+2*1*u₂u₃+2*1*u₃u₁+2*1*u₁u₂=0.

Должно быть действительным уравнение

aA'+bB'+cC'+2fF'+2gG'+2hH'=0

и S и Σ' должны быть неполярными:

-1*1-1*1+(1/g²)*(1/g''²)=0

или

(1/g²)*(1/g''²)=2.

Таким образом, вновь, если справедливо g'=g''=1 и g=1/√2, то обеспечивается неполярность S c S' и Σ'.

Рассмотрение единичного конуса

S'=-1*x₁ ²-1*x₂ ²+1*x₃ ²=0

допускает, таким образом, рассмотрение идентичных обращающихся в нуль инвариантов относительно S:

S=-1*x₁ ²-1*x₂ ²+2*x₃ ²=0

или соответственно

Σ'=1*u₁ ²+1*u₂ ²+1*u₃ ²+2*1*u₂u₃+2*1*u₃u₁+2*1*u₁u₂=0

Тем самым соотношение

a_a' ²:=-1*(-1)²-1*(-1)²+2*1²=-1*1-1*1+2*1=0

является линейным в коэффициентах уравнений

S=-1*x₁ ²-1*x₂ ²+2*x₃ ²=0

и

Σ'=1*u₁ ²+1*u₂ ²+1*u₃ ²+2*1*u₂u₃+2*1*u₃u₁+2*1*u₁u₂=0.

Согласно положению Гильберта об инвариантных телах (Hilbert, стр.291, пар. 2), в нашей системе линейная комбинация

ϕ [-1, -1, 2]*[-1, -1, 1]²+

Θ [-1, -1, 2]*[1, 1, 1]²=0

вновь представляет собой инвариант. Тем самым соответствуют, например, любые пересекающиеся прямые f^(t₁) и f^(t₂), ξ₁ и ξ_2, рассматриваемые на плоскости, проходящей через векторы [-1, -1, 2] и [1, 1, 1], бесконечно многим инвариантам S и S' или соответственно S и Σ'.

Все комбинаторные возможности для положения S, S' и Σ', как нетрудно определить путем подстановки, исчерпываются, таким образом, в отношении результата в той же плоскости.

Практическое применение этой концепции в сигнальной технике позволяет, например, выполнить анализ связи f^(t) или нескольких связей f₁^(t), f₂^(t),…, f_p^(t) по меньшей мере двух сигналов s₁(t), s₂(t),…, s_m(t) или соответственно их передаточных функций t₁(s₁(t)), t₂(s₂(t)),…, t_m(s_m(t)) или также произвольно определяемого отображения f^#(t) или произвольно определяемых отображений f₁ ^#(t), f₂ ^#(t),…, f_µ ^#(t) сигнала s^#(t) или нескольких сигналов s₁ ^#(t), s₂ ^#(t),…, s_Ω ^#(t) посредством определения упомянутых инвариантов. При этом эта связь f^(t) или эти связи f₁^(t), f₂^(t),…, f_p^(t) по меньшей мере двух сигналов s₁(t), s₂(t),…, s_m(t) или соответственно их передаточных функций t₁(s₁(t)), t₂(s₂(t)),…, t_m(s_m(t)) или также произвольно определяемое отображение f^#(t) или произвольно определяемые отображения f₁ ^#(t), f₂ ^#(t),…, f_µ ^#(t) сигнала s^#(t) или нескольких сигналов s₁ ^#(t), s₂ ^#(t),…, s_Ω ^#(t) отображается, например, на комплексной числовой плоскости - в этом случае ось х₁ совпадает, например, с действительной осью, ось х₂ - с мнимой осью, - и затем рассматриваются точки пересечения этих отображений в данном примере с плоскостью, проходящей через векторы (1, 1, -2) и (1, 1, 1) или (-1, -1, 2) и (1, 1, 1), которые представляют собой абсолютные или относительно их статистического распределения точные опорные точки для дальнейшего анализа, обработки и оптимизации. Например, можно согласно СН 01159/09 или РСТ/ЕР2010/055876 или также СН01776/09 или РСТ/ЕР2010/055877 предпринять оптимизацию псевдостереофонических аудиосигналов и затем определить точки пересечения суммы передаточных функций f*[x(t)]=[x(t)/√2]*(-1+i) и g*[y(t)]=[y(t)/√2]*(1+i), см. ниже, с плоскостью, проходящей через векторы (1, 1, -2) и (1, 1, 1) или (-1, -1, 2) и (1, 1, 1). Если эти точки пересечения взвешиваются с помощью подходящего способа, см. детальное описание, то осуществляется параметризация согласно СН 01159/09 или РСТ/ЕР2010/055876 или также СН0176/09 или РСТ/ЕР2010/055877, которая являются особенно предпочтительной для рассматриваемых аудиосигналов.

Согласно одному аспекту рационально использовать (известные как таковые) алгоритмы сжатия или способы сокращения данных, или соответственно рассматривать характеристические признаки, такие как минимум или максимум рассматриваемых сигналов или передаточных функций или связей или отображений, для соответствующей изобретению ускоренной оценки.

Краткое описание чертежей

Различные формы выполнения предложенного изобретения описываются ниже в качестве примера со ссылками на чертежи, на которых показано:

Фиг.1 - схемный принцип известного панорамного потенциометра.

Фиг.2 - характеристика демпфирования левого и правого канала панорамного потенциометра без надбазовой области и соответствующие углы отображения.

Фиг.3 - первый вариант выполнения устройства или способа согласно СН 01159/09 или РСТ/ЕР2010/055876, в котором левый канал L' или правый канал R', получаемые путем стереофонического преобразования, подаются на соответствующий панорамный потенциометр при общих сборных шинах L и R.

Фиг.4 - второй вариант выполнения устройства или способа согласно СН 01159/09 или РСТ/ЕР2010/055876.

Фиг.5 - третий вариант выполнения устройства или способа согласно СН 01159/09 или РСТ/ЕР2010/055876.

Фиг.6 - четвертый вариант выполнения устройства или способа согласно СН 01159/09 или РСТ/ЕР2010/055876 с эквивалентной Фиг.3 схемой с несколько модифицированной MS-матрицей, благодаря которой не требуется непосредственного подключения панорамного потенциометра.

Фиг.7 - схема, эквивалентная Фиг.3-6, если для обратно пропорциональных демпфирований λ и ρ представленного на Фиг.3 панорамного потенциометра справедливо соотношение λ=ρ.

Фиг.8 - расширенная схема согласно Фиг.7 для нормирования уровня выходных сигналов стереофонического преобразователя.

Фиг.9 - пример схемы, которая в качестве расширения Фиг.8, данные сигналы x(t) и y(t) отображает на комплексную числовую плоскость как сумму передаточных функций f*[x(t)]=[x(t)/√2]*(-1+i) и g*[y(t)]=[y(t)/√2]*(1+i).

Фиг.10 - пример схемы, которая в качестве расширения Фиг.9 устанавливает ширину отображения стереофонического сигнала.

Фиг.11 - пример входной схемы для уже имеющегося стереофонического сигнала L°, R° для передачи на схему согласно фиг.12 (для определения локализации сигнала), которая L°, то есть l(t), и R°, то есть r(t), отображает на комплексную числовую плоскость как сумму передаточных функций f*[l(t)]=[l(t)/√2]*(-1+i) и g*[r(t)]=[r(t)/√2]*(1+i).

Фиг.12 - схема для определения локализации сигнала, входы которой могут быть соединены с выходами Фиг.10А или соответственно выходами Фиг.11.

На Фиг.13 показан пример схемы для двух логических элементов для нормирования уровня и для нормирования степени корреляции выходных сигналов стереопреобразователя (например, стереопреобразователя согласно WO 2009/138205 или ЕР 2124486 или ЕР 1850639), причем входной сигнал M и S (перед прохождением включенного перед MS-матрицей усилителя) опционально может подаваться в схему согласно Фиг.20, которая опционально может также подключаться после Фиг.19.

На Фиг.14 показан пример схемы, которая поданные сигналы x(t) и y(t) отображает на комплексную числовую плоскость посредством суммы передаточных функций f*[x(t)] и g*[y(t)] или соответственно определяет аргумент их суммы f*[x(t)]+g*[y(t)].

На Фиг.15 показан пример схемы для выбора области определения посредством параметра а.

На Фиг.16 показан пример схемы для третьего логического элемента, который сигналы, сгенерированные согласно Фиг.13, и отображенные согласно Фиг.14 на комплексную числовую плоскость проверяет относительно допустимой области определения, заново определенной согласно Фиг.15 посредством параметра а, согласно условию Re²{f*[x(t)]+g*[y(t)]}*1/a²+Im²{f*[x(t)]+g*[y(t)]}≤1.

На Фиг.17 показан пример схемы для четвертого логического элемента, который в заключение рассматривает рельеф функции f*[x(t)]+g*[y(t)] в отношении максимизации ее функциональных значений, причем пользователь может свободно выбирать граничное значение R*, определенное неравенством (8аВ) (или соответственно отклонение Δ, определенное неравенством (8аВ)) для этой максимизации.

На Фиг.18 показана входная схема для уже имеющегося стереофонического сигнала перед передачей на схему согласно Фиг.19 для определения локализации сигнала.

На Фиг.19 показана схема для определения локализации сигнала, входы которой соединены с выходами Фиг.17 или соответственно выходами Фиг.18.

На Фиг.20 показан другой пример схемы для нормирования стереофонического или псевдостереофонического сигналов, которая, при подключении после Фиг.19, активируется, как только параметр z представлен в качестве входного сигнала. Начальное значение коэффициента усиления λ соответствует при этом конечному значению коэффициента усиления λ Фиг.13 при передаче параметра z.

На Фиг.21 показан пример схемы, которая отображает поданные сигналы x(t) и y(t) на комплексную числовую плоскость посредством передаточных функций f*[x(t)] и g*[y(t)].

На Фиг.22 показан пример схемы для настройки ширины отображения аудиосигнала.

На Фиг.23 показано условие неполярности для отображений S, S' и Σ'.

На Фиг.24 показаны отображения S, S' и Σ' для прямоугольной системы координат x₁=u₁, x₂=u₂, x₃=u₃ из перспективы первого квадранта соответствующей комплексной числовой плоскости.

На Фиг.25 показаны отображения S, S' и Σ' для прямоугольной системы координат x₁=u₁, x₂=u₂, x₃=u₃ также из перспективы первого квадранта соответствующей комплексной числовой плоскости.

На Фиг.26 показаны отображения S, S' и Σ' для прямоугольной системы координат x₁=u₁, x₂=u₂, x₃=u₃ из перспективы четвертого квадранта соответствующей комплексной числовой плоскости.

На Фиг.27 показан характер сходимости конвергентности весовой функции, которая на данной фигуре, например, на основе средних значений точек пересечения в первом или также третьем квадрантах трех псевдостереофонических отрезков сигнала, отображенных на комплексную числовую плоскость, с плоскостью, проходящей через векторы (1, 1, -2) и (1, 1, 1) или (-1, -1, 2) и (1, 1, 1), оптимизирует параметры φ, f (или n), α, β.

На Фиг.28 показан пример описанной ниже схемы для оптимизации псевдостереофонических сигналов на основе алгебраических инвариантов, которая может быть подключена непосредственно после Фиг.17, и в этом случае может образовывать с ней в данном примере неразделяемый блок. Выходы Фиг.6С внутри всей схемы в этом случае должны обрабатываться таким образом, как если бы они были выходами Фиг.17. Схема согласно Фиг.28 обеспечивает то, что через включенные перед ней элементы могут проходить разные отрезки аудиосигнала. Результатом является параметризация φ, f, α, β, оптимизированная на основе средних значений точек пересечения в первом или также третьем квадрантах этих отрезков сигнала, отображенных на комплексную числовую плоскость, с плоскостью, проходящей через векторы (1, 1, -2) и (1, 1, 1) или (-1, -1, 2) и (1, 1, 1).

На Фиг.29 показан пример схемы, которая на основе определения среднеквадратичной энергии входных сигналов s₁(t_i), s₂(t_i),…, s_δ(t_i) и определенных весов G₁, G₂,…, G_δ осуществляет нормирование этих входных сигналов и непосредственно затем определяет инварианты связи f^(t) или нескольких связей f₁^(t), f₂^(t),…, f_p^(t) этих входных сигналов.

Детальное описание

Сначала поясняются алгебраические основы настоящего изобретения на основе Фиг.23-26.

Фиг.23 представляет собой условие неполярности для S, S' и Σ'. 1001 обозначает условие неполярности для S и S', выраженное через f^~(g'), 1002 - для S и Σ', выраженное через f^~(g''). Точка 1004 пересечения 1001 с диагональю 1003 первого квадранта иллюстрирует совпадение S и S', точка 1005 пересечения для 1001 и 1002 представляет собой искомое условие неполярности; g'=g''=1 можно считывать непосредственно.

На Фиг.24 показаны отображение S (2001), S' (2002) и Σ' (2003), а также плоскость 2004, проходящая через векторы (1, 1, -2) и (1, 1, 1), на которой лежат искомые алгебраические инварианты S и S' или S и Σ', из перспективы первого квадранта соответствующей комплексной числовой плоскости. 2005, 2006 и 2007 показывают плоскости, проходящие через прямоугольную систему координат x₁=u₁, x₂=u₂, x₃=u₃.

На Фиг.25 показаны отображение S (2001), S' (2002) и Σ' (2003), а также плоскость 2004, проходящая через векторы (1, 1, -2) и (1, 1, 1), на которой лежат искомые алгебраические инварианты S и S' или S и Σ', из перспективы первого квадранта соответствующей комплексной числовой плоскости. 2005, 2006 и 2007 показывают плоскости, проходящие через прямоугольную систему координат x₁=u₁, x₂=u₂, x₃=u₃.

На Фиг.26 показаны отображение S (2001), S' (2002) и Σ' (2003), а также плоскость 2004, проходящая через векторы (1, 1, -2) и (1, 1, 1), на которой лежат искомые алгебраические инварианты S и S' или S и Σ', теперь из перспективы четвертого квадранта соответствующей комплексной числовой плоскости. 2005, 2006 и 2007 показывают плоскости, проходящие через прямоугольную систему координат x₁=u₁, x₂=u₂, x₃=u₃.

Общеизвестно, что аудиосигналы, которые излучаются через два или более динамиков, создают у слушателя пространственное впечатление, если они имеют различные амплитуды, частоты, разности времени прихода или разности фаз или соответственно замирают.

Такие декоррелированные сигналы можно, с одной стороны, сгенерировать с помощью по-разному расположенных систем преобразования звука, сигналы которых опционально дополнительно обрабатываются, или посредством так называемых псевдостереофонических методов, которые создают соответствующую декорреляцию, исходя из моносигнала.

Документы СН 01159/09 или соответственно РСТ/ЕР2010/055876 к моменту времени настоящей заявки не были опубликованы. Поэтому в дальнейшем их содержание, для понимания следующего примера выполнения настоящего изобретения, полностью воспроизводится:

Некоторые псевдостереофонические сигналы имеют повышенную «фазность», то есть отчетливо воспринимаемые разности времени прихода между обоими каналами. Часто также степень корреляции между обоими каналами слишком низка (недостаточная совместимость) или слишком высока (нежелательное приближение к монофоническому звучанию). Псевдостереофонические, а также стереофонические сигналы могут, таким образом, иметь недостатки, которые объясняются недостаточной или избыточной декорреляцией излучаемых сигналов.

Таким образом, целью СН 01159/09 или РСТ/ЕР2010/055876 является решить эту проблему и выравнить или, напротив, сильнее дифференцировать стереофонические (включая псевдостереофонические) сигналы.

Другой целью является стремление улучшать, генерировать, передавать, преобразовывать или воспроизводить стереофонические и псевдостереофонические сигналы.

В СН 01159/09 или РСТ/ЕР2010/055876 эти проблемы решаются, в том числе, посредством преимущественно нецелесообразного подключения панорамного потенциометра в устройстве для псевдостереофонического преобразования.

Панорамные потенциометры (также Pan-Pot, панорамные регуляторы) сами по себе известны и применяются для сигналов интенсивностной стереофонии, то есть для стереосигналов, которые различаются исключительно по их уровню, но не по разности времени прихода или разности фаз или разными частотными спектрами. Схемный принцип известного панорамного потенциометра представлен на Фиг.1. Прибор имеет вход 101 и два выхода 202, 203, которые приложены к сборным шинам 204, 205 групповых каналов L (левого аудиоканала) и R (правого аудиоканала). В среднем положении (М) обе сборные шины получают тот же самый уровень, в боковых положениях слева (L) и справа (R) сигнал направляется только в левую или соответственно в правую сборную шину. В промежуточных положениях панорамный потенциометр формирует разности уровней, которые соответствуют различным позициям фантомного источника звука на базе динамиков.

На Фиг.2 показана характеристика демпфирования левого и правого канала панорамного потенциометра без надбазовой области и соответствующие углы отображения. В среднем положении демпфирование в каждом канале составляет 3 дБ, за счет акустического наложения в результате возникает то же впечатление о силе звука, как если бы имелся только один канал в положении L или R.

Панорамные потенциометры могут примерно как делители напряжения делить левый канал в различном выбираемом соотношении на результирующие левый или соответственно правый выходы (эти выходы также обозначаются как сборные шины) или соответственно аналогичным образом делить правый канал в различном выбираемом соотношении на те же левый или соответственно правый выходы (те же самые сборные шины). Тем самым при сигналах интенсивностной стереофонии ширина отображения и их направление могут сдвигаться подходящим образом.

В случае псевдостереофонических сигналов, которые используют разности времени прихода или разности фаз, разные частотные спектры или демпфирование (как и при созданных таким образом стереофонических сигналах в общем случае) такое сужение ширины отображения или соответственно сдвиг направления отображения на основе панорамного потенциометра невозможны. Поэтому от применения панорамных потенциометров для подобных сигналов в основном отказались.

Согласно СН 01159/09 или РСТ/ЕР2010/055876, однако, неожиданным образом и вопреки предшествующему опыту, было установлено, что ранее не известное подключение панорамного потенциометра после схемы псевдостереофонического конвертирования приносит неожиданные преимущества. А именно, такое подключение не может приводить к вышеупомянутому ограничению ширины отображения или к сдвигу направления отображения. Однако степень корреляции между левым и правым сигналом можно таким образом повысить или также снизить с помощью такого панорамного потенциометра.

В предпочтительном варианте выполнения соответствующий панорамный потенциометр подключается к левому и правому выходу схемы для получения псевдостереофонического сигнала. При этом сборные шины обоих панорамных потенциометров используются совместно и предпочтительно идентично.

При этом каждый панорамный потенциометр имеет один вход и два выхода. Вход первого панорамного потенциометра соединен с первым выходом схемы, а вход второго панорамного потенциометра соединен со вторым выходом этой схемы. Первый выход первого панорамного потенциометра соединен с первым выходом второго панорамного потенциометра. Второй выход второго панорамного потенциометра соединен со вторым выходом второго панорамного потенциометра.

Альтернативно и эквивалентно, для настройки степени корреляции вместо панорамных потенциометров можно использовать также первую схему для псевдостереофонического конвертирования со стереопреобразователем и включенным перед ним усилителем для усиления входного сигнала стереопреобразователя, и это без использования панорамных потенциометров. Таким образом, эквивалентная настройка степени корреляции может быть реализована с помощью меньшего количества компонентов.

Альтернативно и эквивалентно, можно степень корреляции варьировать вместо панорамных потенциометров также с помощью второй схемы с модифицированным стереопреобразователем, который содержит сумматор и вычитатель, чтобы входные сигналы (M, S), соответственно усиленные на предопределенные коэффициенты, суммировать или вычитать, чтобы генерировать сигналы, идентичные сигналам сборных шин панорамного потенциометра. Тем самым эквивалентная настройка степени корреляции может быть реализована с помощью еще меньшего числа компонентов.

Это можно применять также к устройствам или способам, которые генерируют сигналы, воспроизводящиеся посредством более чем двух динамиков (например, в относящихся к уровню техники аудиосистем объемного звучания).

На Фиг.3-5 показаны различные варианты выполнения изложенного схемного принципа, при котором соответствующий панорамный потенциометр 311 и 312, 411 и 412, 511 и 512 подключен непосредственно к схеме 309, 409 или 509 псевдоконвертирования. В каждом представленном на данных фигурах примере схема 309, 409 или 509 псевдоконвертирования состоит из схемы с MS-матрицей 310, 410 или 510, как описано в WO 2009/138205 или ЕР 2124486, а также ЕР 1850639.

С помощью этого панорамного потенциометра 311 и 312, 411 и 412, 511 и 512 можно повышать или снижать степень корреляции результирующих сборных шин L 304, 404, 504 и R 305, 405, 505. В соответствии с этим полученный в результате стереопреобразования (после прохождения через MS-матрицу) левый канал L' 302, 402, 502 или соответственно правый канал R' 303, 403, 503 подается на соответствующий панорамный потенциометр в случае совместно используемых сборных шин L и R.

Если демпфирование λ для левого входного сигнала L' панорамного потенциометра 311, 411 или 511 и демпфирование ρ для правого входного сигнала R' панорамного потенциометра 312, 412 или 512 результирующего из устройства 309, 409 или 509 стереофонического сигнала 302 и 303, 402 и 403, 502 и 503 уменьшается до области между 0 и 3 дБ, можно ввести обратно пропорционально соотношения

1≥λ≥0

и

1≥ρ≥0

(причем 1 соответствует значению 0 дБ и 0 соответствует значению 3 дБ).

λ и ρ соответствуют обратно пропорциональным демпфированиям представленных на Фиг.3-5 панорамных потенциометров, уменьшенным до диапазона между 0 и 3 дБ.

Тем самым для результирующих стереофонических сигналов (сборных шин) L и R (304 и 305, 404 и 405, 504 и 505) или соответственно выходных сигналов L'' 313, 413, 513 и R'' 314, 414, 515 панорамного потенциометра 311, 411, 511 и выходных сигналов L''' 315, 415, 515 и R''' 316, 416, 516 панорамного потенциометра 312, 412, 512 получаются соотношения

(1А) L=L''+L'''=½*L'(1+λ)+½*R'(1-ρ)

и

(2А) R=R''+R'''=½*L'(1-λ)+½*R'(1+ρ)

На Фиг.6А показан другой вариант выполнения с эквивалентной Фиг.3А схемой с несколько модифицированной MS-матрицей, для которой не требуется непосредственного подключения панорамного потенциометра. С учетом эквивалентности стереофонического преобразования (MS-матрицирования)

L'=(M+S)*1/√2

и

R'=(M-S)*1/√2

получаются соотношения

(1А) L=[M(2+λ-ρ)+S(λ+ρ)]*1/2√2

(2А) R=[M(2-λ+ρ)-S(λ+ρ)]*1/2√2.

Тем самым сигналы сборных шин L и R также могут выводиться непосредственно из входных сигналов M и S схемы стереофонического преобразования.

Для случая λ=ρ (одинаковые демпфирования в левом и правом каналах) справедливо:

(3А) L=(M+λ*S)*1/√2

(4А) R=(M-λ*S)*1/√2,

то есть вариация амплитуды сигнала S эквивалентна подключению соответствующего панорамного потенциометра при идентичном демпфировании в левом и правом канале. Выходные сигналы L и R соответствуют при этих предпосылках сигналам сборных шин L и R на Фиг.3.

Получается, таким образом, схема или способ примерно согласно варианту с Фиг.6 (причем возможны тривиальные отклонения), которая образует суммарный сигнал из усиленного на коэффициент (2+λ-ρ) М-сигнала и усиленного на коэффициент (λ+ρ) S-сигнала, а также разностный сигнал из усиленного на коэффициент (2-λ+ρ) М-сигнала минус усиленный на коэффициент (λ+ρ) S-сигнал, причем в целом нужна коррекция на коэффициент 1/2√2, чтобы получить сигналы L и R, эквивалентные формулам (1А) и (2В).

На Фиг.7 показана схема, эквивалентная Фиг.3 или Фиг.6, если для обратно пропорциональных демпфирований λ и ρ представленного на Фиг.3 панорамного потенциометра справедливо соотношение λ=ρ. Эту схему не следует путать с известной из интенсивностной стереофонии (MS-микрофонный способ) конфигурацией для изменения угла охвата или раскрыва (которое в данном случае не происходит!).

При этом исходят из того, что часто для выравнивания или дифференцирования стереосигналов для предложенных панорамных потенциометров или описанной выше модифицированной MS-матрицы достаточным является стандартное демпфирование. При λ=ρ упрощается представленное выше устройство согласно приведенным выше формулам (3А) и (4А) до

(3А) L=(M+λ*S)*1/√2

(4А) R=(M-λ*S)*1/√2

что является равноценным простой амплитудной коррекции S-сигнала (717).

Такая амплитудная коррекция S-сигнала до сих пор известна только для классического MS-микрофонного способа, в котором приводит в идеальном диапазоне к изменению угла охвата или раскрыва, которое в данном случае не происходит. Перенос подобного принципа действия невозможен (и применение MS-микрофонного метода в предложенной схеме соответственно не является очевидным).

На Фиг.7, таким образом, осуществляется дополнительное усиление S-сигнала на коэффициент λ(1≥λ≥0) перед заключительным прохождением через MS-матрицу. Результирующий стереосигнал эквивалентен сигналам сборных шин 304 и 305 на Фиг.3, 404 и 405 на Фиг.4, и 504 и 505 на Фиг.5 при стандартном демпфировании, а также выходному сигналу L и R на Фиг.6, если там удовлетворяется λ=ρ.

На практике с помощью этой схемы или соответственно способа можно точно установить степень корреляции, то есть существует непосредственная функциональная связь между демпфированием λ и степенью корреляции r, для которой в идеальном случае справедливо

0,2≤r≤0,7.

Для λ в серии испытаний оказалось предпочтительным для большинства применений соотношение

0,07≤λ≤0,46.

В частности, с помощью этого устройства или способа оказалось нетрудным устранять арт