Способ бесплатформенной инерциальной навигации на микромеханических чувствительных элементах

Способ бесплатформенной инерциальной навигации на микромеханических чувствительных элементах

Иллюстрации

Показать все

Реферат

Изобретение относится к навигационной технике, а именно к способам бесплатформенной инерционной навигации малогабаритных движущихся объектов (например, беспилотных летательных аппаратов), при которых для определения параметров ориентации и навигации объектов используют микромеханические чувствительные элементы (микромеханические акселерометры и гироскопы).

Известен способ бесплатформенной инерциальной навигации малогабаритных объектов, реализованный в устройстве [1] с применением микромеханических акселерометров и гироскопов. Согласно данному способу акселерометры и гироскопы закрепляют по борту подвижного объекта, ориентируют их оси чувствительности параллельно трем ортогональным осям подвижного объекта, измеряют их выходные сигналы, обрабатывают по заданным алгоритмам, в результате чего определяют навигационные параметры (координаты объекта и его скорость), а также параметры ориентации объекта (углы тангажа и рысканья). Недостатком способа является малая точность. Малая точность обусловлена наличием переменных перекрестных связей между чувствительными элементами. Изменение связей происходит при изменении ориентации осей отдельно взятого элемента относительно осей других отдельно установленных микромеханических чувствительных элементов из-за деформации конструкции объекта при движении.

Известен также способ бесплатформенной инерциальной навигации на микромеханических чувствительных элементах, взятый за прототип и реализованный в устройстве [2]. Согласно данному способу, по борту подвижного объекта устанавливают триаду микромеханических акселерометров (три акселерометра в одном корпусе) и триаду микромеханических гироскопов (три гироскопа в одном корпусе). Ориентируют оси триад параллельно трем ортогональным осям подвижного объекта. Измеряют выходные сигналы. Затем производят их обработку по заданным алгоритмам и в результате определяют параметры ориентации и навигации объекта. Недостатками способа-прототипа являются малая точность, малое время работы в заданном диапазоне точности. Указанные недостатки обусловлены особенностью работы микромеханических чувствительных элементов (далее чувствительные элементы), изготавливаемых по технологии микросхем. Особенность заключается в наличии в выходном сигнале чувствительного элемента постоянной составляющей, значение которой изменяется (дрейфует) во времени. Согласно [1, стр. 60 и стр. 114], применение наиболее современных микросхем обеспечивает работу объекта в заданном диапазоне точностей не более одного часа.

Заявленное изобретение решает задачу повышения точности способа бесплатформенной инерциальной навигации на микромеханических чувствительных элементах для малогабаритных подвижных объектов.

Техническим результатом заявленного изобретения является снижение погрешностей измерения совокупности примененных в способе микромеханических чувствительных элементов, что обеспечивает снижение погрешностей определения навигационных параметров и параметров ориентации подвижного объекта и существенное увеличение времени его автономной работы.

Для решения поставленной задачи в способ бесплатформенной инерциальной навигации, заключающийся в том, что на борту подвижного объекта устанавливают микромеханические гироскопы и акселерометры, ориентируют их оси чувствительности относительно трех ортогональных его осей, затем гироскопами измеряют проекции вектора угловых скоростей, акселерометрами - проекции вектора действующего ускорения на оси координат объекта, полученные выходные сигналы фильтруют и вычисляют навигационные параметры, введена последовательность действий, согласно которой на борту подвижного объекта устанавливают n тетрад микромеханических гироскопов и n тетрад микромеханических акселерометров, которые располагают осями чувствительности вдоль диагоналей куба одной механической базы, грани которой ориентируют параллельно ортогональным осям объекта, а измеренные выходные сигналы тетрад преобразуют в проекции сигналов, действующих на ортогональную систему координат объекта.

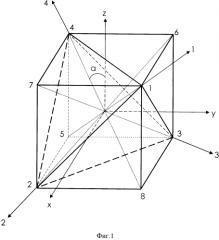
Сущность изобретения поясняется фиг. 1, на которой приведена схема взаимного расположения ортогональной системы координат объекта и системы координат осей тетрады.

Как показано на фиг. 1, механическая база объекта выполнена в виде куба с вершинами 1-8. Оси X, Y, Z представляют собой ортогональную систему координат объекта. Встроенная в куб тетрада имеет вершины 1, 2, 3, 4. При этом оси ортогональной системы координат X, Y, Z проходят через центры граней куба, перпендикулярно к их плоскостям, а оси тетрады 1, 2, 3, 4 расположены вдоль диагоналей куба. В куб можно вписать вторую тетраду между вершинами 5, 6, 7, 8 куба. Оси второй тетрады 5, 6, 7, 8 направлены навстречу осям 1, 2, 3, 4 первой тетрады. Угол α между осями тетрады и ортогональными осями составляет 54,7°.

Проекция вектора физической величины (угловой скорости, ускорения), действующей вдоль оси тетрады на ортогональную ось, имеет коэффициент пропорциональности B=cosα=0,578.

При этом значения физических величин, действующих в системе координат тетрады, пересчитываются в их проекции в ортогональной системе координат согласно системе уравнений

На борту объекта устанавливают n тетрад чувствительных элементов. Причем оси чувствительности элементов располагаются вдоль диагоналей куба механической базы объекта. Если n=1, то оси тетрады совпадают с осями куба 1, 2, 3, 4 (фиг. 1). При n=2 оси одной тетрады совпадают с осями куба 1, 2, 3, 4, а другой тетрады - с осями куба 5, 6, 7, 8. При n=4 две тетрады имеют оси вдоль осей куба 1, 2, 3, 4, а две другие тетрады имеют оси вдоль осей куба 5, 6, 7, 8. Далее в процессе движения объекта выходные сигналы чувствительных элементов тетрад с помощью системы уравнений (1) преобразуют в проекции сигналов, действующих вдоль ортогональной системы координат объекта. При n≠1 производят сложение преобразованных сигналов согласно выражениям:

где x_i, y_i, z_i - величины преобразованных сигналов чувствительных элементов одной тетрады;

n - число установленных тетрад.

В уравнениях (1) сигналы чувствительных элементов, оси которых направлены встречно, вычитаются. В результате преобразований получают три ортогональные проекции вектора угловой скорости, три проекции вектора ускорения.

Затем полученные триады сигналов физических величин фильтруют и обрабатывают по заданным алгоритмам, в результате чего определяют навигационные параметры.

По сравнению со способом, взятым за прототип, точность предлагаемого способа повышается. В способе-прототипе используют триады чувствительных элементов, при этом вдоль одной из ортогональных осей работает только один чувствительный элемент и его погрешности напрямую определяют точность навигации. В предлагаемом способе, согласно уравнениям (1), вдоль каждой из ортогональных осей работают все четыре чувствительных элемента. При этом появляется возможность снизить погрешности навигации существенно ниже погрешностей отдельных чувствительных элементов. Точность определения навигационных параметров и параметров ориентации повышается за счет уменьшения случайной и систематической составляющих. Случайная погрешность создает при нулевом входном сигнале на выходе одного чувствительного элемента напряжение случайного шума U_ш. При совместной работе k чувствительных элементов случайный шум в суммарном сигнале растет пропорционально k . В результате чего напряжение случайного шума при применении n тетрад в сигналах ортогональных осей составит:

где 4 - число чувствительных элементов тетрад;

n - число установленных тетрад.

При действии физической величины на один чувствительны элемент, на его выходе возникает сигнал U_С. В случае применения тетрад выходной сигнал в ортогональных координатах составит:

U_CΣ=4nBU_C.

Поэтому при применении данного способа случайная составляющая сигнала по сравнению с самим сигналом уменьшается в Q раз:

Таким образом, в Q раз падает случайная погрешность измерения.

Кроме того, из-за роста соотношения сигнал-шум при применении данного способа также возрастает в Q раз динамический диапазон измерения физической величины. При этом способ дает возможность уверенно реагировать на меньшие изменения входных физических величин, что по сравнению с прототипом также повышает точность навигации.

Систематические погрешности чувствительного элемента определяются свойствами его амплитудной характеристики: смещение нуля (выходное напряжение при нулевом входном сигнале), температурный коэффициент смещения нуля, нелинейность амплитудной характеристики, крутизна характеристики (отношение выходного напряжения к входному сигналу), температурный коэффициент крутизны. Причем систематические погрешности имеют стабильный характер и имеют знак (+ или -).

Чувствительные элементы могут иметь различные сочетания систематических погрешностей. Но при изготовлении системы из всей массы чувствительных элементов одного типа можно выбрать группы из четырех штук с практически одинаковыми систематическими погрешностями. Из таких групп собирают тетрады чувствительных элементов. При этом из уравнений (1) видно, что в формировании ортогональных сигналов х, y, z принимают участие два сигнала из осей тетрады с положительным знаком, а два с отрицательным. Поэтому при их суммировании с учетом знаков одинаковые систематические погрешности вычитаются. В результате, в сигналах ортогональных осей X, Y, Z систематические погрешности уменьшаются. Степень уменьшения зависит от качества отбора чувствительных элементов.

При использовании n тетрад чувствительных элементов среди отобранных тетрад остатки систематических погрешностей вдоль осей X, Y, Z могут иметь различные сочетания. Но среди отобранных тетрад также отбирают тетрады с практически одинаковыми систематическими погрешностями по абсолютной величине, но с противоположными знаками. При совместном использовании четного количества n тетрад остатки систематических погрешностей будут вычитаться друг из друга. В результате чего систематическая погрешность по сравнению со способом-прототипом уменьшается.

Таким образом, предлагаемый способ позволяет значительно снизить случайные и систематические погрешности определения параметров ориентации и навигации подвижного объекта, что приведет к повышению времени автономной работы объекта.

Кроме того, предлагаемый способ, по сравнению с прототипом, является более надежным. В способе-прототипе при выходе из строя одного из чувствительных элементов тетрады функционирование тетрады прекращается, и способ не реализуется. В предлагаемом способе выход из строя даже одной тетрады из n не мешает его реализации. При этом фиксируется вышедшая из строя тетрада. Признаком исправной работы тетрады является равенство нулю суммы выходных сигналов четырех чувствительных элементов при любом расположении вектора физической величины, воздействующей на тетраду. При неравенстве суммы сигналов нулю данную тетраду исключают из работы, но продолжают использовать для обработки сигналы оставшихся (n-1) тетрад. При этом погрешность измерения параметров ориентации и навигации возрастает незначительно в n n − 1 раз.

В настоящее время на предприятии положительный эффект от внедрения предлагаемого способа проверен авторами опытным путем, при макетировании систем микромеханических акселерометров, состоящих из 4-х и 8-ми тетрад. В результате точность определения суммарного сигнала определяемого выражением (2) для системы из 4-х тетрад была повышена более чем в два раза, для системы, состоящей из 8-ми тетрад, более чем в четыре раза. В настоящее время осуществляются работы по макетированию тетрад на микромеханических гироскопах.

Список литературы

1. Матвеев В.В., Распопов В.Я. Основы построения бесплатформенных инерциальных навигационных систем. // СПб: Государственный научный центр Российской Федерации ОАО «Концерн Центральный научно-исследовательский институт «Электроприбор», 2009, с. 21.

2. Распопов В.Я. и другие. Комплексированные микросистемы ориентации малоразмерных беспилотных летательных аппаратов. // Материалы XVIII Санкт-Петербургской международной конференции по интегрированным навигационным системам. // СПб: Государственный научный центр Российской Федерации ОАО «Концерн Центральный научно-исследовательский институт «Электроприбор», 2011, с. 161.

Способ бесплатформенной инерциальной навигации на микромеханических чувствительных элементах, согласно которому на борту подвижного объекта устанавливают микромеханические гироскопы и акселерометры, ориентируют их оси чувствительности относительно трех ортогональных его осей, затем гироскопами измеряют проекции вектора угловых скоростей, акселерометрами - проекции вектора действующего ускорения на оси координат объекта, полученные выходные сигналы фильтруют и вычисляют навигационные параметры и параметры ориентации, отличающийся тем, что на борту подвижного объекта устанавливают n тетрад микромеханических гироскопов и n тетрад микромеханических акселерометров, которые располагают осями чувствительности вдоль диагоналей куба одной механической базы, грани которой ориентируют параллельно ортогональным осям объекта, а измеренные выходные сигналы тетрад преобразуют в проекции сигналов, действующих на ортогональную систему координат объекта.