Способ монтажа ротора газотурбинного двигателя

Способ монтажа ротора газотурбинного двигателя

Иллюстрации

Показать все

Реферат

Изобретение относится к роторным газотурбинным машинам и может быть использовано при монтаже их роторов, в том числе у высокооборотных газотурбинных двигателей, у которых критические частоты вращения роторов находятся в рабочем диапазоне частот.

Из уровня техники известно, что одной из основных проблем надежной работы газотурбинных машин является устранение резонанса их роторов по изгибной форме колебаний на критических частотах вращения, когда силы, приводящие к прогибу вала ротора (центробежные силы от неуравновешенной массы ротора и гироскопические моменты роторных дисков), становятся равными силам упругого сопротивления вала, вследствие чего его поперечные перемещения из-за увеличения изгиба вала значительно возрастают.

Устранение резонанса роторов на критических частотах их вращения достигается различным образом, например за счет выведения критических частот (отстройка роторов) из рабочего диапазона вращения роторов.

Так, например, известны способы изменения критических частот вращения роторов, при которых они теряют устойчивость (резонанс) за счет изменения конструкции: массовых, геометрических характеристик, жесткостей валов и опор (см. Биргер И.А. Шорр Б.Ф., Иосилевич Г.Б. Расчет на прочность деталей машин. Москва, «Машиностроение», 1979, 431 с., 433 с.).

Данные способы отстройки от резонанса по изгибной форме колебаний для высокооборотных двигателей при наличии критических частот вращения, находящихся в рабочем диапазоне, крайне сложны в реализации. Это связано, в основном, с отсутствием возможности проводить конструктивные изменения на существующих двигателях.

Известен способ монтажа ротора газотурбинного двигателя, согласно которому его устанавливают в подшипниковых опорах качения, причем в одной из его опор используют подшипник роликовый с овальной беговой дорожкой кольца подшипника, связанного силовыми элементами со статором двигателя, а установку подшипника на опоре осуществляют таким образом, что большая ось овала беговой дорожки кольца совпадает с направлением силы тяжести ротора, жесткость опоры выбирают из условия C>13,3·δω_k ²/µ_min, а параметр овала Δ задают в диапазоне от минимального и до максимального значения.

Минимальное значение определяют из условия

,

где δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; J_O - момент инерции ротора при его угловом перемещении относительно опоры с круговыми дорожками качения подшипника; β - коэффициент, равный β=f_K/f_C; - коэффициент, равный ; f_K и f_C - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора; L - пролет ротора; С - жесткость опоры; Δ_min - минимальный параметр овала дорожки качения кольца подшипника, Δ_min=(D_max-D_min)/2; µ_min - минимальный параметр овала дорожки качения кольца подшипника, µ_min=(D_max-D_min); D_max и D_min - максимальный и минимальный диаметр овальной дорожки качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; g - ускорение свободного падения; Т - время оборота ротора.

Максимальное значение параметра овала определяют также по данной зависимости только при β=1.35 и и оно равно µ_max=L²(12,896·δ-13,132·m·g/ω_K ²)/J_O, где µ_max - максимальный параметр овала дорожки качения кольца подшипника, µ_max=(D_mах-D_min) (см. патент РФ №2528789, кл. F02C 7/06, F01D 25/16, 2014 г.) - наиболее близкий аналог.

В результате анализа известного способа необходимо отметить, что при его реализации, в процессе работы двигателя при вращении ротора, круговое перемещение вектора центробежной силы от его неуравновешенной массы в зонах кольца подшипника с овальной дорожкой качения, где радиус-вектор его контура изменяется в направлении действия силы и это приращение превышает радиальное перемещение вала ротора на опоре, приводит к тому, что реакция опоры будет отсутствовать.

Полное отсутствие реакции опоры за время, равное четверти периода собственных колебаний ротора, приведет к тому, что прогиб вала устранится, и это явление будет предотвращать потерю устойчивости ротора при критической частоте вращения.

Устранение прогиба вала при овальной беговой дорожке качения кольца подшипника будет происходить в двух четвертях оборота вала, где радиус-вектор контура кольца возрастает, а для внутреннего кольца - уменьшается.

В двух других четвертях реакция опоры восстановится, и в этот период ротор будет находиться в режиме, который подвержен потере устойчивости, но, так как этот процесс будет чрезвычайно кратковременным, потери устойчивости ротора не произойдет.

Однако при монтаже вала ротора в подшипнике с овальной дорожкой качения кольца, при котором большая ось дорожки совпадает с направлением силы тяжести ротора, обеспечивается устранение резонанса ротора при критической частоте его вращения только при достаточно жестких опорах, что не позволяет применить для монтажа ротора податливые упруго-демпферные опоры с малой жесткостью в связи с ограничениями возможности применения данного способа, а использование которых является весьма перспективным, так как их применение позволяет осуществить гашение колебаний роторов практически на любых частотах возбуждения, что повышает стабильность работы двигателя.

Техническим результатом настоящего изобретения является повышение эффективности работы двигателя путем повышения его надежности и срока эксплуатации за счет уменьшения или полного гашения колебаний его ротора практически во всем диапазоне частот вращения, в том числе за счет обеспечения возможности использования при монтаже ротора упругодемпферных опор.

Указанный технический результат обеспечивается тем, что в способе монтажа ротора газотурбинного двигателя, согласно которому вал ротора посредством подшипников качения устанавливают с возможностью вращения в опорах, причем для монтажа вала ротора в одной из опор используют подшипник роликовый с овальной беговой дорожкой его кольца, связанного силовыми элементами со статором двигателя, а установку этого подшипника в опоре осуществляют таким образом, что одна из осей овала беговой дорожки кольца совпадает с направлением силы тяжести ротора, и задают жесткость опоры и параметр овала беговой дорожки кольца подшипника, при которых обеспечивается устранение резонанса ротора на критических частотах его вращения, новым является то, что установку подшипника с овальной беговой дорожной его кольца в опоре осуществляют таким образом, что с направлением силы тяжести ротора совпадает малая ось овала беговой дорожки, жесткость опоры выбирают из условия C>13,3·(δω_k ²-mg)/µ_min, а параметр овала µ, равный разности максимального и минимального диаметров задают в диапазоне от минимального значения и до максимального значения µ_max=L²(12.896·δ-2.882·m·g/ω_K ²)/J_O, где δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; J_O - момент инерции ротора при его угловом перемещении относительно опоры с круговыми дорожками качения подшипника; λ - параметр, равный λ=1,234·β²+0,761·β⁴+0,118β; η - параметр, равный ; β - коэффициент, равный β=f_K/f_C; - коэффициент, равный ; f_K и f_C - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора; L - пролет ротора; С - жесткость опоры; µ - параметр овала дорожки качения кольца подшипника, µ=(D_max-D_min); D_max и D_min - максимальный и минимальный диаметр овальной дорожки качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; g - ускорение свободного падения.

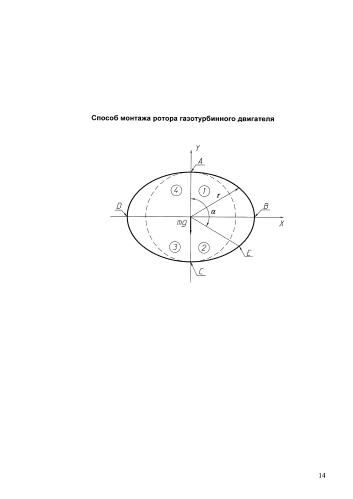
Сущность заявленного способа поясняется чертежом, на котором представлена схема силовых воздействий ротора при его вращении на опору с овальной дорожкой качения кольца подшипника, цифрами 1-4 пронумерованы квадранты.

Заявленный способ осуществляют следующим образом.

При монтаже ротора двигателя его вал устанавливают в опоры, выполненные в статоре двигателя. Для обеспечения вращения ротора относительно статора монтаж ротора в опорах осуществляют посредством подшипников качения. Согласно заявленному способу, для монтажа ротора в опорах, в одной из опор устанавливают подшипник роликовый с овальной беговой дорожкой внешнего кольца, связанного силовыми элементами со статором двигателя. Для обеспечения достижения указанного выше технического результата важно установить в опоре подшипник с овальной беговой дорожкой заданного параметра овала строго определенным образом, а также подобрать жесткость опоры, при которой обеспечивается устранение резонанса ротора на критических частотах его вращения.

Для гашения резонанса ротора на критической частоте его вращения, установку подшипника с овальной беговой дорожкой его кольца в опоре устанавливают таким образом, что с направлением силы тяжести ротора совпадает малая ось овала беговой дорожки.

Весьма важным для достижения указанного технического результата является определение жесткости опоры (С), которая должна соответствовать следующему условию: C>13,3·(δω_k ²-mg)/µ_min, где ω_кр - критическая круговая скорость вращения ротора; µ_min - минимальное значение параметра овала дорожки качения кольца подшипника, при котором реализуется технический результат, µ_min=(D_max-D_min); D_max и D_min - соответственно максимальный и минимальный диаметр овальной дорожки качения; δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; g - ускорение свободного падения.

Как показали исследования, при меньшем значении жесткости существенно снижается диапазон частот вращения ротора, при котором обеспечивается гашение колебаний.

При проведении исследований установлено, что параметр овала дорожки подшипника должен находиться в определенном интервале от своего минимального до максимального значения, причем данные значения должны соответствовать приведенным ниже зависимостям. Минимальное значение параметра овала должно соответствовать равенству , а максимальное - равенству µ_max=L²(12.896·δ-2.882·m·g/ω_K ²)/J_O, где δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; J_O - момент инерции ротора при его угловом перемещении относительно опоры с круговыми дорожками качения подшипника; λ - параметр, равный λ=1,234·β²+0,761·β⁴+0,118β; η - параметр, равный ; β - коэффициент, равный β=f_K/f_C; - коэффициент, равный ; f_K и f_C - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора; L - пролет ротора; µ - параметр овала дорожки качения кольца подшипника, µ=(D_max-D_min); D_max и D_min - максимальный и минимальный диаметр овальной дорожки качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; g - ускорение свободного падения.

При значении жесткости опоры ниже указанного значения существенно снижается диапазон частот вращения ротора, при котором обеспечивается гашение колебаний, а при большем - наблюдалось хаотичное движение вала ротора в опоре, что ухудшало его работу на критических частотах.

Осуществление приведенной выше совокупности признаков при монтаже ротора способствует тому, что в процессе работы двигателя круговое перемещение вектора центробежной силы от неуравновешенной массы ротора в зонах кольца, где радиус-вектор контура наружного кольца подшипника возрастает, реакция опоры будет отсутствовать и вал распрямляется.

Отсутствие воздействия на вал ротора реакции опоры за время, равное четверти периода собственных колебаний ротора, приводит к тому, что прогиб вала устраняется, что предотвращает потерю устойчивости ротора при критической частоте вращения. Как показали исследования, для предотвращения потери устойчивости ротора достаточно, чтобы было обеспечено устранение прогиба при вращении вала в одной четверти его оборота.

При использовании для монтажа ротора упругих опор с определенной податливостью (обратная величина жесткости) в процессе работы двигателя в точке А под действием центробежной силы от неуравновешенной массы ротора происходит упругое смещение опоры. При круговом вращении ротора и его центробежной силы от точки А за отрезок времени Δt точка контакта вала выходит на контур несмещенного кольца и реакция опоры устраняется (см. чертеж).

Упругое смещение опоры на малой оси овала определяется как отношение центробежной силы ротора на опоре δω_K ² от его дисбаланса δ, уменьшенное на величину собственного веса ротора, приходящегося на опору к - жесткости опоры "С"

.

Уравнение контура кольца овальной формы описывается тригонометрической функцией

,

где R_O - радиус кольца подшипника по малой оси овала; Δ_min - параметр овала; ω_k - круговая скорость вращения ротора на критической частоте.

Представляя отклонение овального контура дорожки качения внешнего кольца от радиуса на меньшей оси овала в виде Δ_minsin(ω_kt), раскладывая в ряд Тейлора с учетом малого значения ω_KΔt, получаем sin(ω_kt)=ω_kt.

Для выполнения условия малости аргумента при устранении реакции на опоре и условия, когда не будет преодолен предельный угол посадки вала ротора на опору, принимаем ω_kΔt=0,15 и приравняем упругое вдавливание вала на малой оси к отклонению контура овала в точке устранения реакции

.

Из последнего выражения получаем минимальное значение жесткости опоры для выполнения условия малости аргумента при выходе вала ротора на контур недеформируемой опоры

,

где µ_min - минимальное значение параметра овала, µ_min=2Δ_min=(D_max-D_min).

При данном расположении овала дорожки качения упругое смещение опоры от центробежных сил уменьшается за счет веса ротора, который направлен в противоположном направлении относительно центробежной силы в момент устранения реакции на опоре, что как раз и позволяет использовать опоры с меньшей жесткостью.

При соответствии жесткости данному условию посадка вала ротора на опору до полного распрямления вала при овальной беговой дорожке наружного кольца будет реализовываться при допустимом угле удаления от точки В (см. чертеж), не превышающем критический , и хаотического движения вала ротора на опоре происходить не будет.

Минимально допустимая жесткость опоры связана с параметром овала беговой дорожки подшипника. Это обусловлено тем обстоятельством, что при большем параметре овала µ величина упругого смещения опоры в начальный момент устранения реакции на опоре точке А (см. чертеж) допускается больше, а следовательно, жесткость опоры может быть ниже.

Определим минимальное значение параметра овала беговой дорожки внешнего кольца подшипника с учетом податливости опоры, при котором реализуется устранение прогиба вала и резонанса ротора. Центробежная сила в точке А (см. чертеж) компенсируется реакцией опоры. При круговом движении центробежной силы вал ротора через интервал времени Δt выходит на контур недеформируемой опоры, реакция опоры пропадает, и вал находится под действием только центробежной силы.

С этого момента начинает нарастать радиальное перемещение вала на опоре с овальной дорожкой качения. Радиальные перемещения от центробежной силы на податливой опоре будут такими же, как и для абсолютно жесткой опоры только при увеличении времени до посадки вала ротора на опору на величину Δt.

Посадка вала ротора при минимальном параметре овала на абсолютно жестких опорах, при котором обеспечивается устранение прогиба вала в течение четверти периода свободных колебаний ротора, происходит при угле посадки, равном

,

где β - параметр, определяющий посадку вала ротора при условии полного устранения прогиба вала, β=fк/fc; fк - критическая частота вращения ротора, при которой он теряет устойчивость; fc - собственная частота колебаний ротора на двух опорах.

Посадка вала ротора на упругоподатливых опорах при минимальном параметре овала происходит при значении параметра β, увеличенного на β′, определяемого из условия α=0.15=β′·π/2

.

Перемещение вала ротора при совпадении малой оси овала с направлением силы тяжести ротора от статического и динамического дисбаланса, а также перемещение вала ротора от скорости, которую он получил за время Δt до посадки его на опору, будет таким же, как и при совпадении большой оси овала с направлением силы тяжести ротора (см. патент РФ №2528789, кл. F02C 7/06, F01D 25/16, 2014 г.).

Перемещение вала ротора от его собственного веса установим за время, определяемое с момента устранения реакции и до посадки вала ротора на опору. Данное перемещение с достаточной точностью можно определить в интервале времени от t₁=0 до (См. Ю.Б. Назаренко. Устранение резонанса на критической частоте вращения роторов при эллиптической траектории вращения оси вала на опоре // Авиационно-космическая техника и технология. - Харьков: ХАИ. - 2013. №10(107), 63 с.), и оно составит

,

где m - масса ротора, приходящаяся на опору с овальной дорожкой качения

,

m_i и x_i - масса и координата диска относительно опоры с круговыми дорожками качения; J_O - суммарный момент инерции ротора при его колебании относительно опоры с круговыми дорожками качения, ; β - коэффициент, равный β=f_K/f_C; f_K и f_C - критическая частота вращения ротора и собственная частота колебаний ротора; - коэффициент, равный ; ω_k - круговая критическая скорость вращения ротора; L - пролет ротора, g - ускорение свободного падения.

Минимальное значение параметра овала, при котором устраняется резонанс, определенное с учетом центробежных сил, собственного веса и с учетом перемещения от скорости, полученной в момент устранения реакции, составит

,

где Δ_min - минимальный параметр овала, Δ_min=(D_max-D_min)/2; δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения.

Минимальное значение параметра овала µ, равное разности максимального D_max и минимального D_min диаметра составит

,

где λ - параметр, определяемый из выражения λ=(1.234·β²+0.761·β⁴+0.118β); η - параметр, равный .

Если параметр овала меньше указанного минимального значения, то, как показали исследования, полного распрямления вала за четверть периода собственной частоты колебаний ротора не произойдет и резонанс не устранится.

Максимальное значение параметра овала Δ_max определяется при большем значении параметра β, чем при посадке в точке Е, равном β=1.35 и , при котором работа ротора будет стабильной, а при большем значении может наступить хаотичное его движение (см. патент РФ №2528789, кл. F02C 7/06, F01D 25/16, 2014 г.)

,

Статический дисбаланс ротора на опоре с овальной дорожкой качения определяется на балансировочной установке с технологическим подшипником с круговыми кольцами при диаметре беговой дорожки наружного кольца, равном минимальному диаметру овальной дорожки качения.

При большем значении максимального значения параметра овала посадка вала на опору происходит при критическом угле удаления от точки В (см. чертеж), и наступает хаотичное движение вала ротора на опоре, что дополнительно ухудшает работу ротора на критической частоте.

Заявленный способ будет более понятен из приведенного ниже примера.

Пример реализации способа проведен на моделе, представляющей собой полый стальной стержень, имитирующий вал, на котором закреплены три разнесенных по его длине стальных диска, имитирующих ротор. Стержень посредством подшипников качения смонтирован на опорах, в одной из которых установлен роликовый подшипник с овальной дорожкой качения.

После монтажа стержня в опорах два диска расположены на удалении от опор на расстоянии L/4 и один - посередине полого стержня. Длина стержня составляет L=0,5 м, внешний и внутренний его диаметры равны 80 мм и 60 мм. Массы каждого диска (m₁, m₂, m₃) одинаковы и равны 10,2 кг, диаметр диска D=300 мм и его толщина t=20 мм. Дисбаланс имитированного ротора, приходящийся на опору с овальной дорожкой качения, равен δ=6 г·см.

С учетом принятых исходных данных собственная частота колебаний стержня с дисками на двух опорах составила f_C=291,4 Гц, а критическая частота вращения вала - 315,6 Гц (См. Ю.Б. Назаренко, А.Ю. Потапов. Способ устранения резонанса ротора турбореактивного двигателя при критической частоте его вращения с помощью овализации дорожки качения неподвижного кольца роликового подшипника // Двигатель. №1, 2012. - С. 17).

Для устранения резонанса при критической скорости вращения ротора ω_k=1983 рад/с при параметре β=1.08, определяющем угол посадки вала на опоре, минимальный параметр овала равен µ_min=18 мкм. При меньшем параметре овала не происходило полного устранения прогиба стержня и резонанса имитируемого ротора.

Максимальное значение параметра овала на опоре равно µ_max=57 мкм. При большем параметре овала наблюдалось хаотичное движение вала ротора в опоре, что ухудшало работу имитируемого ротора на критических частотах.

Задавалась минимально допустимая жесткость опоры, которая составляла С>C_min=3.1·10⁷ H/м.

Критические скорости вращения ротора составляли: ω_K=1876.6 рад/с (минимально допустимая) и ω_k=1983 рад/с (фактическая).

При поименованных выше параметрах колебаний имитируемого ротора в процессе его вращения практически не наблюдалось.

Аналогичная картина имела место при овальной дорожке качения неподвижного внутреннего кольца, которое устанавливалось на опору. При угловом перемещении вектора центробежной силы от неуравновешенной массы ротора в зонах кольца подшипника на участках с уменьшением радиуса дорожки качения внутреннего кольца и при приращении смещения контура к оси вращения, превышающем радиальное перемещение вала ротора на опоре в этом же направлении, реакция на вал со стороны опоры отсутствовала. В течение времени, равного четверти периода собственных колебаний ротора, вал ротора распрямлялся. Применительно к графическим материалам, если вектор центробежной силы от неуравновешенной массы ротора направлен на четвертый квадрант в направлении от центра (чертеж), то посадка вала ротора на внутреннее кольцо будет осуществляться в третьем квадранте. В этом случае силы тяжести ротора уменьшают радиальное перемещение ротора, и параметры овала были такими же, как и для неподвижного наружного кольца при посадке вала ротора во втором квадранте.

Применение данного способа позволяет гарантировано обеспечить полное распрямление вала в одном из квадрантов за четверть периода собственных колебаний ротора и, тем самым, предотвратить резонанс ротора на критических частотах его вращения, в том числе при использовании упругодемпферных опор.

Способ монтажа ротора газотурбинного двигателя, согласно которому вал ротора посредством подшипников качения устанавливают с возможностью вращения в опорах, причем для монтажа вала ротора в одной из опор используют подшипник роликовый с овальной беговой дорожкой его кольца, связанного силовыми элементами со статором двигателя, а установку этого подшипника в опоре осуществляют таким образом, что одна из осей овала беговой дорожки кольца совпадает с направлением силы тяжести ротора, и задают жесткость опоры и параметр овала беговой дорожки кольца подшипника, при которых обеспечивается устранение резонанса ротора на критических частотах его вращения, отличающийся тем, что установку подшипника с овальной беговой дорожной его кольца в опоре осуществляют таким образом, что с направлением силы тяжести ротора совпадает малая ось овала беговой дорожки, жесткость опоры выбирают из условия C>13,3·(δω_k ²-mg)/µ_min, а параметр овала µ задают в диапазоне от минимального значения μ min = 2 L 2 ⋅ ( λ ⋅ δ − η ⋅ m ⋅ g / ω K 2 ) / [ sin ( π ⋅ β ¯ / 2 ) ⋅ J O ] и до максимального значения µ_max=L²(12.896·δ-2.882·m·g/ω_K ²)/J_O, где δ - статический дисбаланс ротора, приходящийся на опору с овальной дорожкой качения; J_O - момент инерции ротора при его угловом перемещении относительно опоры с круговыми дорожками качения подшипника; λ - параметр, равный λ=1,234·β²+0,761·β⁴+0,118β; η - параметр, равный η = − 0.637 ⋅ β ¯ 5 + 1.244 β ¯ 4 − 1.42 β ¯ 3 + 2.016 ⋅ β ¯ 2 − 0.161 ⋅ β ¯ ; β - коэффициент, равный β=f_K/f_C; β ¯ - коэффициент, равный β ¯ = β + 0,095 ; f_K и f_C - критическая частота вращения ротора и собственная частота колебаний ротора; ω_k - круговая критическая скорость вращения ротора; L - пролет ротора; C - жесткость опоры; µ - параметр овала дорожки качения кольца подшипника, µ=(D_max-D_min); D_max и D_mjn - максимальный и минимальный диаметр овальной дорожки качения; m - масса ротора, приходящаяся на опору с овальной дорожкой качения; g - ускорение свободного падения.