Профиль зубчатого колеса, обеспечивающий передачу постоянного крутящего момента

Профиль зубчатого колеса, обеспечивающий передачу постоянного крутящего момента

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение, в целом, относится к колесам и шестеренкам, образующим зубчатую передачу наручных часов, а именно к профилю зубьев подобных колес и подобных шестеренок. Настоящее изобретение также относится к часовым механизмам и часовым устройствам, содержащим колеса и шестеренки согласно изобретению.

Уровень техники

Известно, что в наручных часах колебания пружинного баланса никогда не бывают идеально изохронными. Другими словами, продолжительность колебаний не является полностью независимой от их амплитуды. Также известно, что если общий угол колебаний баланса превышает предельное значение, то ось ролика баланса может упираться во внешнюю часть вилки, что существенно ускоряет ход часов. В этом случае говорят, что часы спешат. Из вышесказанного следует, что желательно максимально выровнять амплитуду колебаний баланса.

Изменения амплитуды колебаний спирального баланса могут быть вызваны разными причинами. С одной стороны, хорошо известно, что интенсивность трения, которому подвергаются оси баланса, увеличивается при перемещении часов из горизонтального положения в вертикальное. С другой стороны, также хорошо известно, что изменения усилия, передаваемого спусковым механизмом на баланс, могут вызывать изменения амплитуды колебаний баланса.

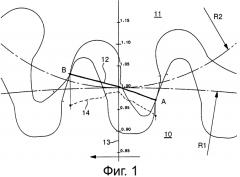
Причины изменения усилия, передаваемого со спускового механизма на баланс, могут быть разными. Во-первых, натяжение пружины заводного барабана зависит от степени завода последнего. Обычно это приводит к изменению усилия, передаваемого зубчатой передачей, в функциональной зависимости от резерва мощности. С другой стороны, в зубчатом зацеплении точка касания между профилями боковых частей двух зацепляющихся зубьев перемещается радиально во время хода зуба, поднимаясь к вершине ведущего зуба. Данное явление схематически изображено на прилагаемой фиг.1, где показано зацепление ведущего колеса 10, имеющего восемьдесят два зуба и радиус R1 начальной окружности, с приводным колесом 11, имеющим двенадцать зубьев и радиус R2 начальной окружности. Стрелкой показано направление вращения. Линия точек касания, именуемая линией 12 зацепления, проходит от точки А до точки В и пересекает две начальные окружности колес вблизи линии 13 центров, соединяющей центры двух колес. В известных зубчатых передачах при перемещении точки касания ведущего колеса с ведомым колесом вдоль линии зацепления соотношение между переданным крутящим моментом и принятым крутящим моментом не является постоянным. В свою очередь, во время хода зуба подобное соотношение меняется, как это показано на примере кривой 14, относительно вертикальной центральной координаты, изображенной на фиг.1.

В часовом механизме именно зубчатая передача передает усилие с заводного барабана на спусковой механизм. Известно, что подобная зубчатая передача является мультипликаторной зубчатой передачей. Поэтому если анкерное колесо, расположенное по ходу после зубчатой передачи, обычно перемещается на несколько тактов в секунду, то часть зубчатой передачи, расположенная по ходу спереди, в этот момент едва передвигается. В подобной ситуации за один ход зуба, расположенного по ходу спереди зубчатой передачи, может происходить значительное число колебаний баланса. Таким образом, следует понимать, что длительности изменения крутящего момента, передаваемого за время хода одного зуба, расположенного по ходу спереди зубчатой передачи, обычно бывают достаточными для того, чтобы повлиять на амплитуду колебаний баланса.

Наконец, усилие, передаваемое со спускового механизма на баланс, также может меняться от одного часового устройства к другому, даже если подобные часовые устройства теоретически являются идентичными. На самом деле, из-за высокой степени миниатюризации, присущей наручным часам и часостроению, производственные допуски при расположении колес и шестеренок наручных часов, по существу, вполне могут влиять на усилие, передаваемое зубчатой передачей наручных часов. Причина этого заключается в том, что при передаче крутящего момента с использованием известных профилей зубчатых колес величина крутящего момента существенно различается, если расстояние между осями вращения двух зубчатых колес отклоняется от теоретического значения. Наиболее серьезный недостаток подобной чувствительности зубчатого зацепления к изменению расстояния между осевыми центрами заключается в том, что необходимо замерять в течение длительного времени амплитуду колебаний баланса каждого механизма наручных часов для обеспечения точности хода.

В часовой области и в часостроении профиль зубьев зубчатых колес и грани шестеренок обычно определяются на основе геометрических кривых, например циклоидальных, эпициклоидальных, гипоциклоидальных или эвольвент окружности. Полученные подобным образом колеса и шестеренки обладают параметрами, обеспечивающими «пропорциональную передачу» или, другими словами, передачу скорости вращения, которая остается постоянной в течение одного хода зуба. Помимо этого, колеса и шестеренки, имеющие зубья, профиль которых очерчен по эвольвенте окружности, обладают дополнительными параметрами, обеспечивающими пропорциональную передачу с одинаковым передаточным числом, даже если расстояние между осями двух колес отклоняется от теоретического значения.

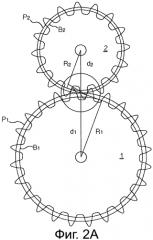
На фиг.2А, где изображено эвольвентное зубчатое зацепление, показано зацепление колеса 1, имеющего двадцать четыре зуба, с колесом 2, имеющим шестнадцать зубьев. На фиг.2А также показаны две концентрические окружности, наложенные на каждое из двух колес. Меньшая из этих двух окружностей (соответственно обозначенных ссылочными позициями В1 и В2) является основной эвольвентной окружностью. Большая окружность (соответственно обозначенная ссылочными позициями Р1 и Р2) является начальной окружностью. Начальная окружность Р1 колеса 1 и начальная окружность Р2 колеса 2 по определению являются касательными. Кроме этого, отношение радиусов d₁ и d₂ начальных окружностей выбирается равным передаточному отношению. Следует заметить, что, в отличие от радиусов d₁ и d₂ начальных окружностей, радиусы R₁ и R₂ двух основных окружностей В1 и В2 не зависят от расстояния между центрами двух колес. Между тем, по определению они имеют такое же отношение, как d₁ и d₂.

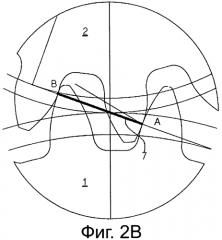
Линия 7 зацепления также показана на фиг.2А и 2В. Можно заметить, что в приведенном примере линия зацепления является отрезком прямой линии, разграниченным двумя точками А и В. Также можно заметить, что по отличительному признаку эвольвентного зубчатого зацепления прямая линия, противолежащая линии 7 зацепления, является точно касательной к двум основным окружностям В1 и В2. Другим отличительным признаком эвольвентного зубчатого зацепления является то, что общая нормаль к кромкам двух зубьев в точке касания всегда направлена в сторону линии зацепления (фиг.2В). Преимущественным признаком эвольвентного зубчатого зацепления является то, что отношение между угловыми скоростями ведущего и ведомого колеса остается постоянным и не зависит от расстояния между центрами осей колес. Другими словами, как уже отмечалось, признаком эвольвентного зубчатого зацепления является то, что оно обеспечивает пропорциональную передачу, с одинаковым передаточным числом, даже если расстояние между осями двух колес отклоняется от теоретического значения. Может возникнуть желание сделать из вышесказанного вывод о том, что крутящий момент, передаваемый эвольвентным зубчатым зацеплением, остается постоянным во время хода зуба, вне зависимости от расстояния между осевыми центрами двух колес. Однако при этом не учитываются силы трения, которые неизбежно возникают при потере равновесия зубчатого зацепления. На самом деле вращение колес всегда сопровождается скольжением касающихся поверхностей относительно друг друга, а следовательно, и силами трения, направленными по касательной к боковым поверхностям двух соприкасающихся зубьев. Следует понимать, что подобные силы трения направлены перпендикулярно общему перпендикуляру к кромкам двух зубьев в точке касания. Силы трения, таким образом, заставляют передаваемое усилие отклоняться от линии зацепления. Со ссылкой на фиг.3, которая аналогична фиг.2В, показаны усилия, создаваемые кромками, соприкасающимися друг с другом (подобные усилия обозначены двумя противоположными стрелками, берущими начало в точках касания между двумя зубьями). Можно заметить, что направление подобных усилий не является коллинеарным с линией зацепления. В результате расхождения между усилием и линией зацепления передаваемый крутящий момент не является постоянным во время хода зуба.

На самом деле, можно показать, что для передачи постоянного крутящего момента необходимо, чтобы с начала до конца хода зуба усилие в месте касания между двумя зубьями было постоянно направлено в одну и ту же точку линии центров (обозначенную ссылочной позицией Р₀ на фиг.8А, 8В и 8С). Таким образом, из вышесказанного следует понимать, что эвольвентное зубчатое зацепление может передавать постоянный крутящий момент только в том случае, если соприкасающиеся зубья будут скользить относительно друг друга без трения.

Раскрытие изобретения

Задача настоящего изобретения, таким образом, заключается в устранении недостатков, присущих предшествующему уровню техники, за счет использования профиля зубчатых колес, обеспечивающего передачу постоянного крутящего момента во время хода зуба, даже если расстояние между осями двух колес отклоняется от теоретического значения. Данная задача решена в настоящем изобретении за счет использования, с одной стороны, колеса или шестеренки по п.1 формулы изобретения, а, с другой стороны, часового механизма или часового устройства, содержащего колеса и шестеренки согласно изобретению.

Краткое описание чертежей

Другие признаки и преимущества настоящего изобретения станут очевидны из следующего описания, предлагаемого исключительно в качестве иллюстративного и не ограничивающего примера, со ссылкой на прилагаемые чертежи.

На фиг.1 показан частичный, схематический вид известного зубчатого зацепления;

на фиг.2А - схематический вид известного эвольвентного зубчатого зацепления;

на фиг.2В - частичный, увеличенный схематический вид эвольвентного зубчатого зацепления, показанного на фиг.2А;

на фиг.3 - схематический вид, аналогичный виду по фиг.2В, на котором также показано действие сил, создаваемых зубьями при их соприкосновении друг с другом в точке касания;

на фиг.4 - частично схематический вид зубчатого зацепления согласно настоящему изобретению в момент, когда точка касания между двумя зубьями совпадает с линией центров;

на фиг.5 - соотношение между положением точки касания между двумя зубьями вдоль линии центров и средней производительностью зубчатого зацепления;

на фиг.6 - угол наклона кромок зубьев в точке касания при проходе линии центров;

на фиг.7 - функциональная вершина и основание кромок зубьев двух колес зубчатого зацепления;

на фиг.8А, 8В и 8С - три последовательных положения, на которых фактически показано, что в зубчатом зацеплении согласно настоящему изобретению направление передаваемого усилия всегда пересекает линию центров в одной и той же точке;

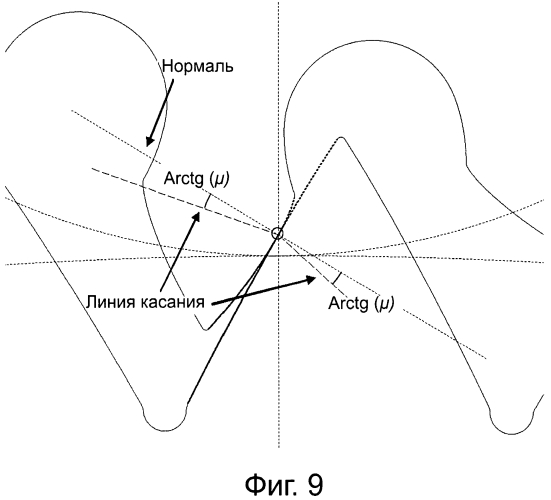
на фиг.9 - схематический вид, аналогичный виду по фиг.8В, на котором показана линия зацепления, образуемая двумя прямолинейными участками;

на фиг.10А, 10В и 10С - три частичных схематических вида, на которых соответственно показаны зацепления одной и той же пары колес, расположенных на трех разных расстояниях друг от друга;

на фиг.11 - график, на котором показаны три кривые, соответственно отображающие изменения крутящего момента, передаваемого во время хода зуба в трех положениях по фиг.10А, 10В и 10С;

на фиг.12А и 12В - зубчатое зацепление согласно второму варианту осуществления настоящего изобретения в двух разных положениях во время хода зуба.

Осуществление изобретения

На фиг.4 схематически показан частичный вид зубчатого зацепления согласно настоящему изобретению в момент, когда точка касания (ссылочная позиция Р₀) между двумя зубьями 17, 18 расположена на линии центров. Далее кратко описаны этапы проектирования зубчатой передачи, показанной на фиг.4.

Рассматриваемый процесс начинается с того момента, когда значение определенных параметров уже известно (или задано). К числу подобных параметров относятся следующие:

- номинальное расстояние d между осевыми центрами;

- допуск для расстояния между осевыми центрами или, другими словами, интервал [dmin, dmax], в котором профили зубьев должны обеспечивать передачу постоянного крутящего момента;

- количество зубьев z₁ и z₂ у каждого из двух колес;

- коэффициент µ трения в точке касания между двумя зубьями.

1. На первом этапе определяют КПД ε зубчатой передачи.

Если крутящий момент, передаваемый колесом 1 на колесо 2, обозначен M_1→2, a противодействие колеса 2 на колесо 1 обозначено M_2→1, то работа (энергия), передаваемая колесом 1 на колесо 2, во время хода зуба будет равна 2π/z₁ M_1→2, а энергия, получаемая колесом 2, будет равна 2π/z₂ M_2→1. При этом условии, если получаемый КПД равен ε, то тогда 2π/z₂ M_2→1=ε 2π/z₁ M_1→2 или ε = M 1 → 2 M 2 → 1 z 1 z 2 .

Для создания профиля согласно изобретению необходимо выбрать средний КПД ε. Предпочтительно выбирать значение ε, близкое к 1, например, в промежутке [0.9; 0.99].

Если d₁ является расстоянием между центром колеса 1 и Р₀, т.е. пересечением между линией центров и линией зацепления, a d₂ является расстоянием между центром колеса 2 и Р₀, то очевидно, что M 1 → 2 M 2 → 1 d 2 d 1 . На самом деле, с одной стороны, сила F_1→2, передаваемая колесом 1 на колесо 2, равна силе F_2→1 противодействия колеса 2 на колесо 1, но с другой стороны, в момент, когда точка касания находится на линии центров, М_2→1=d₁ sinβ F_2→1, a M_1→2=d₂ sinβ F_1→2 (где β - это угол между линией действия силы и линией центров).

Положение точки Р₀ касания на линии центров зависит, таким образом, от значения КПД ε в отношении d 2 d 1 = ε z 2 z 1 , где d₁+d₂=d. На фиг.5 данное отношение изображено графически.

2. На втором этапе выбирается угол наклона зубьев.

Так же как и у профилей известных зубчатых колес, необходимо выбрать наклон зубьев. Как показано на фиг.6, в данном примере наклон кромок зубьев выбирается в точке Р₀ касания на линии центров. Наклон может быть выражен в виде угла α между касательной к одному из зубьев в Р₀ и линией центров. Подобный угол предпочтительно выбирается в диапазоне от 10 до 30°.

3. На третьем этапе рассчитываются радиусы R₁ и R₂ для осиновых окружностей.

В данном примере функциональная (или полезная) часть кромки каждого зуба образована из двух частей, а и b; полезной вершины и полезного основания. Как показано на фиг.7, основание и вершина соединяются в точке Р₀, являющейся общей для двух зубьев во время соприкосновения. Функциональная часть кромки зуба колеса 1 образована полезным основанием, обозначенным ссылочной позицией a₁, и полезной вершиной, обозначенной ссылочной позицией b₁. Аналогичным образом, функциональная часть кромки зуба колеса 2 образована полезным основанием, обозначенным ссылочной позицией а₂, и полезной вершиной, обозначенной ссылочной позицией b₂.

Также со ссылкой на фиг.4, в дополнение к фиг.7, следует понимать, что вначале основание a₁ кромки зуба ведущего колеса (колеса 1) выталкивает вершину b₂ кромки зуба ведомого колеса (колеса 2). Затем вершина b₁ выталкивает основание а₂. Кроме этого, сила трения, возникающая между кромками двух соприкасающихся зубьев, меняет направление после того, как точка касания проходит через линию центров или, другими словами, сила трения меняет направление в точке Р₀. Следовательно, коэффициент µ трения считается отрицательным до пересечения линии центров (трение между частями a₁ и b₂) и положительным после этого (трение между частями b₁ и a₂).

Радиусы R₁ и R₂ основной окружности двух колес получают при помощи следующих формул:

R₁=d₁ cos(α-arctg(µ));

R₂=d₂ cos(α-arctg(µ)).

Зуб, таким образом, образован двумя частями разных профилей, как, например, у циклоид. На самом деле, поскольку знак коэффициента трения изменяется в Р₀, то для каждого зуба будет два радиуса R(a) и R(b) основной окружности. Радиус основной окружности части а и радиус основной окружности части b кромки зуба. Согласно настоящему изобретению профили двух частей а и b касаются в точке Р₀.

4. На четвертом этапе рассчитываются профили частей а и b каждого зуба.

Части а и b зубьев каждого колеса рассчитываются по следующим формулам:

x ( y ) = R 1 [ cos ( 1 μ ln ( 1 − μ u ) ) − u sin ( 1 μ ln ( 1 − μ u ) ) ] ,

y ( u ) = R 1 [ sin ( 1 μ ln ( 1 − μ u ) ) + u cos ( 1 μ ln ( 1 − μ u ) ) ]

Можно заметить, что два отношения выше дают следующий результат: x²+y²=R²(1+u²).

В приведенной выше формуле радиус R основной окружности определяется в соответствии с описанием выше. С другой стороны, параметр u изменяется в интервале [0, 1/µ]. Изменение u обеспечивает прохождение кривой. Для каждой части определяется первоначальное значение (u_ini) переменной u для того, чтобы соответствующая радиальная координата была равна d₁ (для колеса 1) и d₂ (для колеса 2) или, другими словами, таким образом, чтобы значение u_ini соответствовало Р₀. Поскольку для каждой части а₁, b₁, а₂ и b₂ зуба существует разное значение R, то соответственно для каждого зуба и для каждой части а или b первоначальное значение переменной u_ini будет разным. Каждая часть а или b каждого зуба 1 или 2 проходит от Р₀, изменяя значение и от u_ini в сторону увеличения или уменьшения таким образом, чтобы профиль проходил «в правильном направлении» (т.е. с радиальным уменьшением координат для частей а и радиальным увеличением координат для частей b).

Кроме этого, следует отметить, что при этом также необходимо осуществлять вращение профилей, полученных при помощи вышеуказанных формул для x и y, чтобы смещать каждую часть а или b профиля каждого колеса 1 или 2 в положение, при котором точка касания будет находиться на линии центров.

5. На пятом этапе определяются размеры частей а и b.

За счет изменения первоначального значения u_ini переменной u в интервале [0,1/µ] можно увеличивать длину частей а и b: до бесконечности - для частей b (что соответствует значению u, стремящемуся к 1/µ) и до радиуса R основной окружности - для частей а (что соответствует предельному значению u=0). Значения u_fin переменной u, определяющие длину данных частей, просто выбираются таким образом, чтобы с учетом допусков расстояний между осевыми центрами касание между двумя зубьями всегда происходило вдоль функциональных или полезных частей а и b кромок зуба, независимо от расстояния между осевыми центрами. Специалист в данной области техники также обеспечит, чтобы профиль одного зуба не заходил за профиль другого зуба колеса. Для этого он может изменять как угол λ наклона кромок зубьев, так и КПД ε зубчатой передачи.

6. На шестом этапе происходит добавление оснований и вершин зубьев. В приведенных выше формулах описаны лишь функциональные части профиля зубьев, т.е. область, в которой может происходить соприкосновение между зубьями. Между тем, необходимо завершить формирование зубьев, дополнив каждый зуб «нефункциональной» вершиной и т.п., а также основаниями, которые соединяются с основаниями соседних зубьев. При добавлении подобных нефункциональных частей важно, чтобы они не мешали функциональным областям во время зацепления. Примеры цифровых значений:

- номинальное расстояние между осевыми центрами d=2.958 мм;

- интервал расстояний между осевыми центрами [dmin, dmax]=[2.913 мм, 2.968 мм];

- количество зубьев у каждого из двух колес z₁=82 и z₂=12;

- коэффициент трения µ=0.2;

- передаваемая часть крутящего момента: ε=0.966;

- угол наклона: α=30.5°.

Из приведенных выше значений следует, что:

- для части a₁

R=1.932 мм, u_ini=0.894, a u_fin=0.821;

- для части а₂

R=0.346 мм, u_ini=0.348, a u_fin=0.013;

- для части b₁

R=2.447 мм, u_ini=0.348, a u_fin=0.408;

- для части b₂

R=0.273 мм, u_ini=0.894, а u_fin=1.162.

На фиг.8А, 8В и 8С показаны три последовательных положения во время хода зуба в зубчатой передаче согласно изобретению. На фиг.8А показано положение, при котором точка касания находится перед линией центров, а на фиг.8С показано положение, при котором точка касания находится после линии центров. На фиг.8В показано промежуточное положение, при котором точка касания находится на линии центров. На фиг.8А и 8С показано, что сила противодействия противоположных поверхностей направлена не перпендикулярно, а наклонно. Кроме этого, поскольку скольжение поверхностей относительно друг друга с обеих сторон от точки зацепления направлено в противоположные стороны, отклонение направления силы относительно нормали также проходит в противоположном направлении с обеих сторон от точки зацепления.

Как можно убедиться из фиг.8А, 8В и 8С, направление силы в точке касания связано с точкой Р₀ пересечения в течение всего времени зацепления двух кромок. Данный признак является обязательным условием для обеспечения передачи постоянного крутящего момента. Как уже отмечалось, одно из преимуществ профилей зубчатых колес согласно изобретению заключается в том, что крутящий момент всегда передается примерно постоянным образом, даже если расстояние между центрами двух колес отличается от теоретического.

Аналогично фиг.8В, на фиг.9 показано положение, при котором точка касания находится непосредственно на линии центров. На фиг.9 линия зацепления обозначена прерывистой линией. Можно заметить, что в отличие от эвольвентного зацепления, в зубчатом зацеплении согласно настоящему изобретению линия зацепления образована из двух прямолинейных участков, которые соединяются в точке Р₀. Также следует понимать, что направление линии зацепления соответствует в каждой точке направлению силы. Наконец, можно уточнить, что угол между линией зацепления и нормалью, являющийся общим для двух соприкасающихся кромок, равен касательной дуге коэффициента трения.

На фиг.10А, 10В и 10С представлены три частичных схематических вида, на которых соответственно показаны зацепления одной и той же пары колес, расположенной на трех разных расстояниях друг от друга. В свою очередь, на графике, изображенном на фиг.11, показано изменение крутящего момента, передаваемого во время хода зуба для трех разных расстояний между осевыми центрами соответствующих фиг.10А, 10В и 10С. Кривая, показанная непрерывной линией, соответствует номинальному расстоянию между осевыми центрами и соответственно ситуации, изображенной на фиг.10А; кривая, показанная точечной линией, соответствует ситуации, изображенной на фиг.10В; и, наконец, кривая, показанная пунктирными линиями и точками, соответствует ситуации, изображенной на фиг.10С.

В зубчатом зацеплении по фиг.10А расстояние между центрами двух колес соответствует теоретическому значению. В данном «идеальном» случае, во время прохода линии центров точка касания между зубьями находится непосредственно на границе между частью а и частью b кромки каждого из колес. В данном случае, как показывает кривая в виде непрерывной линии по фиг.11, передаваемый крутящий момент является практически постоянным.

В зубчатом зацеплении по фиг.10В расстояние между центрами двух колес больше теоретического значения. В зубчатом зацеплении на фиг.10С расстояние между центрами двух колес меньше теоретического значения. Как показывает кривая по фиг.11 в виде точек, а также кривая в виде прерывистых линий и точек, передаваемый крутящий момент остается практически постоянным, тогда как расстояние между осевыми центрами отклоняется от номинального значения, за исключением пространства вокруг перехода линии центров. На самом деле, когда расстояние между колесами не соответствует номинальному расстоянию между осевыми центрами, две переходные точки между основаниями и вершинами двух соприкасающихся зубьев никогда точно не совпадают. В этом случае переход точки касания от одной полезной части к другой не происходит одновременно для двух зубьев. Подобная неравномерность вызывает временное изменение передаваемого крутящего момента.

На фиг.12А и 12В показаны три последовательных положения во время хода зуба в зубчатом зацеплении согласно второму варианту осуществления настоящего изобретения. Согласно данному второму варианту осуществления изобретения функциональная часть кромки одного зуба содержит только один профиль, а не два, как в варианте осуществления изобретения, изображенном на фиг.7-11.

Предположив, что ведущим колесом является колесо 101, а ведомым колесом - колесо 102, на фиг.12А и 12В можно заметить, что два зуба соприкасаются только после линии центров. В этом случае, при соблюдении тех же условий, что описаны выше, можно сказать, что коэффициент µ трения всегда будет положительным. На самом деле, соприкосновение между кромками всегда происходит после линии центров (однако следует понимать, что при вращении колес в обратном направлении, когда колесо 102 становится ведущим колесом, а колесо 101 - ведомым колесом, соприкосновение между кромками всегда будет происходить перед линией центров, а не после).

Преимущество только что рассмотренного второго варианта осуществления настоящего изобретения заключается в том, что при передаче крутящего момента удается избежать переходных изменений, связанных с неравномерностью, описанной выше для первого варианта осуществления изобретения.

Предлагаемое изобретение позволяет теоретически добиться изменений, абсолютно равных нулю (0%). Между тем, изменения все же могут наблюдаться, если расстояние между осевыми центрами отличается от нормы или из-за того, что коэффициент трения может отличаться у разных частей или с течением времени. Тем не менее, заявителю удалось вычислить, что подобные изменения, безусловно, будут меньше, чем у существующих профилей.

1. Зубчатая передача, содержащая первое колесо с первыми зубьями и второе колесо со вторыми зубьями, причем первые зубья выполнены с возможностью зацепления со вторыми зубьями, причем точки касания образуют линию (12) зацепления, при этом функциональная часть кромки каждого зуба первых зубьев имеет первый профиль, соответствующий параметрической двойной формуле (в прямоугольной декартовой системе координат): где R₁=d₁ cos(α-arctg(µ)), при этом α является углом наклона кромок зубьев в точке касания на линии, которая соединяет центры первого и второго колес и именуется линией центров, a d₁ является расстоянием между центром первого колеса и пересечением между линией центров и линией зацепления,при этом функциональная часть кромки каждого зуба вторых зубьев имеет второй профиль, соответствующий параметрической двойной формуле (в прямоугольной декартовой системе координат): где R₂=d₂ cos(α-arctg(µ)), a d₂ является расстоянием между центром второго колеса и пересечением между линией центров и линией зацепления;при этом µ является параметром, который соответствует коэффициенту трения в точке касания между функциональной частью кромки зуба первых зубьев и функциональной частью кромки зуба второго колеса, при этом µ может находиться в диапазоне от 0,05 до 0,5, а u является переменной, которая изменяется в интервале (0, 1/µ) таким образом, что за счет изменения и происходит переход первого и второго профилей.

2. Зубчатая передача по п. 1, у которой первая функциональная часть и вторая функциональная часть упомянутой кромки каждого зуба первых зубьев являются смежными, а профиль каждой из них соответствует параметрической двойной формуле: где параметр d₁ является одинаковым для первой и второй частей, причем µ считается положительным для первой части и отрицательным для второй, при этом первая функциональная часть и вторая функциональная часть упомянутой кромки каждого зуба вторых зубьев являются смежными, а профиль каждой из них соответствует параметрической двойной формуле: где параметр d₂ является одинаковым для первой и второй частей, причем µ считается положительным для первой части и отрицательным для второй, при этом параметр α и абсолютная величина µ являются одинаковыми для четырех функциональных частей.

3. Зубчатая передача по п. 1, у которой функциональная часть кромки каждого зуба первых зубьев содержит полностью функциональную часть упомянутой кромки каждого зуба первых зубьев.

4. Зубчатая передача по п. 3, у которой функциональная часть кромки каждого зуба вторых зубьев содержит полностью функциональную часть упомянутой кромки каждого зуба вторых зубьев.