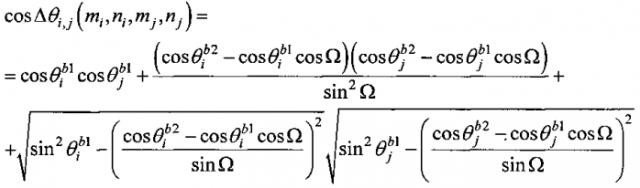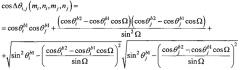Способ определения угловой ориентации летательного аппарата в среде глобальных радионавигационных систем

Способ определения угловой ориентации летательного аппарата в среде глобальных радионавигационных систем

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области навигации по сигналам космических аппаратов глобальных радионавигационных спутниковых систем и может быть использовано для определения угловой ориентации летательного аппарата в пространстве. Известны способы определения ориентации объектов по сигналам космических аппаратов глобальных радионавигационных систем, основанные на приеме сигналов от космических аппаратов антеннами количеством не менее трех, расположенных на объекте так, чтобы они не лежали на одной прямой, при этом антенны принимают сигналы от космических аппаратов, на основе которых определяются разности фаз несущей частоты сигналов, принимаемых на разнесенные антенны, в которых (разностях фаз) содержится информация об углах между направлениями на космические аппараты и векторами, образованными антеннами, на основе которой с привлечением информации о расположении антенн относительно объекта решается задача ориентации, при этом антенны принимают сигналы от трех космических аппаратов, а информация о координатах объекта и космических аппаратов известна [1, 2, 3].

Недостатком способа является необходимость проведения разновременных измерений фазовых сдвигов между разнесенными антеннами объекта, что увеличивает время, требуемое для определения углового положения.

Известен способ определения угловой ориентации объекта по сигналам глобальных спутниковых радионавигационных спутниковых систем [4], основанный на приеме сигналов от космических аппаратов глобальных спутниковых радионавигационных спутниковых систем на разнесенные антенны, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, подборе значений целочисленных неоднозначностей измерений фазовых сдвигов, решении системы уравнений для определения угловой ориентации, при этом искомая угловая ориентация объекта определяется из условия максимума функции правдоподобия.

Недостатком способа является просмотр большого количества комбинаций целочисленных неоднозначностей измерений фазовых сдвигов, в котором не учитывается информация о положении космических аппаратов, векторов, соединяющих антенны.

Задачей изобретения является сокращение количества комбинаций при использовании переборного метода разрешения фазовой неоднозначности при определении углов между направлениями на космические аппараты и векторами, образованными линиями, соединяющими антенны, и использование функции правдоподобия, которая учитывает положение космических аппаратов и векторов, образованных линиями, соединяющими антенны.

Поставленная задача решается тем, что в способе определения угловой ориентации по сигналам космических аппаратов глобальных спутниковых радионавигационных систем, основанном на приеме сигналов от космических аппаратов на антенны, количеством не менее трех, расположенные на объекте так, чтобы они не лежали на одной прямой, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, подборе целочисленных неоднозначностей, позволяющем определить возможные значения угловой ориентации, определении значения искомой угловой ориентации объекта по максимуму функции правдоподобия, согласно изобретению возможные значения угловой ориентации определяют с использованием измеренных фазовых сдвигов и выражений, учитывающих положение космических аппаратов, векторов, образованных линиями, соединяющими антенны, и их взаимную связь.

Предлагаемый способ поясняется фигурами 1÷6.

На фиг. 1 показана прямоугольная Земная система координат и показана связь прямоугольных и геодезических координат.

Фиг. 2 иллюстрирует ориентацию нормальной земной системы координат относительно Земной системы через геодезические координаты.

На фиг. 3 показана ориентация антенн относительно системы координат пеленгатора.

На фиг. 4 показана схема пеленгации двух источников излучения.

На фиг. 5 показана ориентация системы координат пеленгатора относительно связанной системы координат летательного аппарата.

Фиг. 6 иллюстрирует порядок определения углов курса, тангажа и крена летательного аппарата в нормальной земной системе координат.

Угловая ориентация объекта через углы крена, курса и тангажа определяется в нормальной (земной) системе координат в соответствии с [5]. Нормальная земная система координат связана с земной системой координат, в которой осуществляют определение координат объектов в среде ГНСС.

Земная система координат OXYZ - правая прямоугольная декартовая система координат, начало и оси которой фиксированы по отношению к Земле. Начало системы координат расположено в центре масс Земли, ось OZ направлена в Международное условное начало (условному земному полюсу, как определено рекомендациями Международной службы вращения Земли), ось ОХ лежит в плоскости начального астрономического меридиана, установленного Международным бюро времени (в точку пересечения плоскости экватора и начального меридиана), ось OY дополняет систему до правой (ПЗ-90.11).В этой системе координат положение точки в пространстве определяется значениями координат X, Y, Z (см. фиг. 1). Геодезические координаты В, L, Н относятся к общеземному эллипсоиду. При этом центр общеземного эллипсоида совпадает с центром масс Земли, его малая полуось (ось вращения) совмещена с осью OZ, а оси ОХ и OY расположены в плоскости экватора так, что ось ОХ проходит через начальный меридиан. Общеземная система координат вращается вместе с Землей. Геодезическая широта В определяется как угол между нормалью к эллипсоиду, проходящей через заданную точку и плоскостью экватора; геодезическая долгота L - двугранный угол между плоскостью начального меридиана и плоскостью меридиана, проходящего через точку (положительное направление счета долгот от начального меридиана к востоку, от 0° до 360°); геодезическая высота Н - отрезок нормали к общеземному эллипсоиду от его поверхности до точки. Положительные значения высот соответствуют точкам, расположенным над эллипсоидом.

Нормальная (земная) система координат O_gX_gY_gZ_g - земная система координат, ось которой O_gY_g направлена вверх по местной вертикали, а ось O_gZ_g направлена на восток, ось O_gX_g совпадает с направлением на север. Под местной вертикалью понимают прямую, совпадающую с направлением силы тяжести в рассматриваемой точке (см. фиг. 2).

Сущность предлагаемого способа можно пояснить следующим образом. На объекте устанавливают пеленгатор, который имеет, например, три антенны (антенн может быть три и более, но для простоты понимания рассматриваются три антенны). Угол между вектором r_AB, образованными антеннами А, В, и вектором r_АС, образованным антеннами А, С, равен Ω, при этом расстояния между антеннами А, В и А, С (базы) равны соответственно |r_AB|=b₁, |r_AC|=b₂.

Антенны А, В, С располагаются в плоскости OX_пZ_п системы координат OX_пY_пZ_п, в которой направление оси ОХ_п совпадает с направлением вектора r_AB, ось OY_п перпендикулярна плоскости расположения антенн, а ось OZ_п дополняет систему координат до правой (см. фиг. 3).

Антенны принимают сигналы от трех космических аппаратов и более, например от k космических аппаратов R₁, R₂, R_3, …, R_k, по которым определяются координаты космических аппаратов объекта в земной системе координат и измеряются разности фаз сигналов и здесь

i - номер космического аппарата

- разность фаз сигналов, принимаемых антеннами А, В от космического аппарата S_i, излучающего сигнал с длиной волны λ_i;

- разность фаз сигналов, принимаемых антеннами А, С от космического аппарата S_i, излучающего сигнал с длиной волны λ_i (верхний индекс относится к указанию, на какой базе выполнено измерение, а второй - номер космического аппарата).

Схема пеленгации двух источников излучения показана на фиг. 4.

Зная в земной системе координат координаты космических аппаратов с номерами объекта и разности фаз сигналов принимаемых антеннами А, В и А, С, запишем выражения, характеризующие углы между векторами баз, образованными антеннами r_АВ=r_B-r_А, r_АС=r_C-r_А, где r_А, r_B, r_C - координаты антенн в земной системе координат, и векторами наблюдения источников излучения r_0i=r_i-r₀, r_0j=r_j-r₀.

Угол между векторами наблюдения космических аппаратов с номерами i, j равен:

Угол между векторами r_АВ, r_АС, образованными антеннами А, В и А, С, равен:

Для величин расстояний между антеннами |r_AB|, |r_АС| и величин векторов наблюдения КA |r_0i|, |r_0j| выполняются условия

Выполнение этих условий позволяет считать фронт принимаемой электромагнитной волны плоским, и, соответственно, для измеренных разностей фаз принятых сигналов выражения для пеленгов источников излучения космических аппаратов i, j имеют вид:

здесь - целочисленные значения из множеств:

где М_i - целое число длин волн λ_i, укладывающихся на длине b₁;

N_i - целое число длин волн λ_i, укладывающихся на длине b₂;

M_j - целое число длин волн λ_j, укладывающихся на длине b₁;

N_j - целое число длин волн λ_j, укладывающихся на длине b₂.

Выражение для углового расстояния между источниками излучения через пеленги источников относительно векторов баз и угла Ω их взаимной ориентации, имеет вид:

здесь и далее i, j - номера источников излучений;

- пеленг i-го источника, определенный на первой базе и на второй базе;

- пеленг j-го источника, определенный на первой базе и на второй базе.

Выражение для углового расстояния между векторами баз пеленгатора как функция от значений пеленгов и величины угла Δθ_i,j между источниками излучения имеет вид:

Для пеленгов как функций от значений параметров фазовой неопределенности существуют следующие выражения:

Вариант 1 для условия:

- пеленг j-го источника по второй базе через пеленги i-го источника и пеленг j-го источника по первой базе равен:

- пеленг i-го источника по первой базе через пеленги j-го источника и пеленг i-го источника по второй базе равен:

- пеленг i-го источника по второй базе:

- пеленг j-го источника по первой базе:

Вариант 2 для условия:

- пеленг j-го источника по второй базе через пеленги i-го источника и пеленг j-го источника по первой базе равен:

- пеленг i-го источника по первой базе через пеленги j-го источника и пеленг i-го источника по второй базе равен:

- пеленг i-го источника по второй базе:

- пеленг j-го источника по первой базе:

Расчеты угловых расстояний Ω, Δθ_i,j осуществляются с ошибками, измерения пеленгов возмущены ошибками измерения разностей фаз и, как следствие, принятие решения о выборе соответствующих параметров устранения фазовой неоднозначности становится вероятностной процедурой.

Определим функцию правдоподобия как условную плотность вероятности параметров неоднозначности при измеренных значениях пеленгов и заданных угловых расстояниях между векторами баз (Ω) и источниками излучения (Δθ_i,j). В допущении нормального закона распределения погрешностей измерений косинусов углов пеленгации, угла между векторами баз и угла между векторами наблюдения источников излучения функция правдоподобия имеет вид:

где σ_Ω, - среднеквадратическая погрешность оценки косинусов углов Ω, Δθ_i,j по измерениям на объекте установки и расчетах по данным эфемерид космических аппаратов;

- среднеквадратическая погрешность измерения косинусов пеленгов источников k=i, j на базах b=b1, b2;

Δ - невязки соответствующих переменных равные:

Максимум функции правдоподобия соответствует минимуму значения показателя экспоненты, то есть он соответствует минимуму функции, определенной как сумма показателей экспонент:

Из полученного набора возможных значений с параметрами неоднозначности выбираются параметры при которых достигается минимум что соответствует максимуму функции правдоподобия. При параметрах фазовой неопределенности, равных значения с максимальной вероятностью соответствуют истинным значениям пеленгов источников излучения.

Критерий поиска решения, соответствующий максимуму функции правдоподобия, может быть использован при наличии взаимной корреляции погрешностей измерений и законах распределения ошибок, отличающихся от нормального закона. В этом случае изменяется вид функции правдоподобия, однако поиск оптимального решения по-прежнему базируется на поиске максимума функции правдоподобия, учитывающей положение космических аппаратов, векторов, соединяющих антенны, пеленги космических аппаратов и их взаимную связь.

Переборный алгоритм устранения фазовой неоднозначности, реализующий автономное рассмотрение по каждой базе, требует выполнения просмотра (2М_i+1) значений восстановления полных фазовых задержек для одной базы и (2N_i+1) значений для второй базы, таким образом, должны рассматриваться (2М_i+1)(2N_i+1) комбинаций положения источника излучения в пространстве, из которых выбирается одно, удовлетворяющее критерию выбора. Количество комбинаций, равное (2M+1)(2N+1), пропорционально площади прямоугольника со сторонами (2b₁/λ+1, 2b₂/λ+1).

Условие пеленгования источника по двум базам (например, когда базы ортогональны, то есть Ω=90°), а именно, существование пересечения конусов возможных положений источника в пространстве по первой и второй базам при параметрах неоднозначности (m, n) имеет вид: где и Для этого случая количество комбинаций параметров (m, n) пропорционально площади эллипса с полуосями Коэффициент уменьшения просматриваемых комбинаций, определяемый как отношение возможных комбинаций параметров уточненного алгоритма устранения фазовой неоднозначности к количеству комбинаций возможных неоднозначностей по базам, оценочно равен обратной величине отношения площади прямоугольника к площади, вписанного в него эллипса, то есть равен π/4.

Выражение для углового расстояния между двумя источниками излучения определяется при двух условиях:

что соответствует условию существования источников сигналов на пеленгах, равных и при пеленгации их одновременно двумя базами. В этом случае коэффициент уменьшения комбинаций параметров неоднозначности равен произведению коэффициентов уменьшения комбинаций параметров неоднозначности по каждой базе, то есть он оценочно равен чем достигается поставленная цель - уменьшение количества просмотра комбинаций неоднозначности при переборном методе устранения фазовой неоднозначности при определении углов между направлениями на космические аппараты и векторами, образованным антеннами.

Направляющие косинусы векторов наблюдения источников сигналов относительно летательного аппарата в земной системе координат имеют вид:

Пусть неизвестные направляющие косинусы векторов баз в земной системе координат равны:

для первой базы -

для второй -

тогда система уравнений пеленгации источников излучения на первой базе имеет вид:

система уравнений пеленгации источников излучения на второй базе имеет вид:

Введем обозначения:

Система уравнений относительно неизвестных направляющих косинусов вектора базы примет вид:

Система уравнений методом подстановки сводится к решению квадратного уравнения относительно переменной z вида:

Az²+2Bz+С=0

Корни уравнения:

отсюда: х_1,2=u_xz_1,2+ν_x

y_1,2=u_yz_1,2+ν_y

здесь

В=u_xv_x+u_yν_y

D=d₁₁d₂₂-d₂₁d₁₂

Первое решение для направляющих векторов базы:

второе решение:

Решение для направляющих векторов второй базы выполняется аналогично и так же получается два решения относительно направляющих косинусов вектора второй базы соответственно: и

Выбор правильного решения осуществляется путем привлечения результатов измерений по третьему источнику излучения. Для этого определяется вторая пара источников, в которой хотя бы один не использовался при нахождении направляющих косинусов векторов баз, и для нее повторяется процедура выбора параметров неоднозначности и решение задачи определения направляющих косинусов баз. Из полученных значений направляющих косинусов векторов баз за истинное значение принимаются значения, совпадающие в решениях по первой паре и второй паре источников излучения.

По значениям направляющих косинусов векторов баз вычисляются параметры фазовых неоднозначностей источников сигналов космических аппаратов, которые не были использованы при определении ориентации. Для источника l параметры неоднозначности равны:

здесь - направляющие косинусы вектора наблюдения источника сигнала l относительно летательного аппарата в геоцентрической системе координат;

int[…] - операция определения целого числа, ближайшего к целой части операнда;

sign(…) - функция принимает нулевое значение при положительном значении операнда и равна единице в противном случае.

После определения параметров неоднозначностей для всех источников осуществляется решение системы уравнений для определения уточненной угловой ориентации векторов баз с учетом всей совокупности фазовых сдвигов принятых сигналов.

Система уравнений, описывающая связь измеренных фазовых сдвигов с расчетными значениями, которые определяются через направляющие косинусов векторов наблюдения источников излучения и баз пеленгатора, имеет вид:

здесь - номера космического аппарата;

- оценки косинусов пеленгов через измеренные полные фазовые задержки на базах, равные соответственно

e_0i×e_b1, e_0i×e_b2, - скалярные произведения направляющих косинусов векторов наблюдения источников сигнала i-го космического аппарата и неизвестных векторов баз, равные по определению косинусам углов между соответствующими векторами, равные:

последние три уравнения - уравнения связи, которые определяют ориентацию векторов баз относительно друг друга и условие нормировки направляющих косинусов векторов.

В результате решения этой системы уравнений находятся уточненные направляющие косинусы векторов баз в земной системе координат по результатам измерений разностей фаз сигналов от всех космических аппаратов.

По определению направляющие косинусы орта оси ОХ_П системы координат OX_пY_пZ_п совпадают с направляющими косинусами первой базы, то есть Второй орт определяющий положение оси OY_П системы координат, находится как векторное произведение векторов е_b1 и е_b2

здесь ⊗ - операция векторного произведения.

Третий орт e_Zп, определяющий положение оси OZ_П и дополняющий ориентацию осей системы координат OX_пY_пZ_п до правой, определяется векторным произведением векторов e_Xп и e_Yп:

Орты совпадают с осями связанной с пеленгатором системы координат и определяют ориентацию ее относительно земной системы координат.

Преобразование координат из земной системы координат в нормальную (земную) систему координат и обратно осуществляется с использованием соотношений [9]:

здесь - элементы сдвига (координаты центра нормальной системы координат в земной системе координат), равные:

а - большая полуось эллипсоида, м;

α - сжатие эллипсоида;

В - долгота;

L - широта.

Связь прямоугольных пространственных координат X, Y, Z и геодезических L, В, Н описывается формулами:

где X, Y, Z - прямоугольные координаты точки;

L, В, H - геодезические координаты точки (соответственно широта и долгота в рад, и высота в м);

N - радиус кривизны первого вертикала, м;

е - эксцентриситет эллипсоида.

Значения радиуса кривизны первого вертикала и квадрата эксцентриситета эллипсоида вычисляют соответственно по формулам:

е²=2α-α²

где а - большая полуось эллипсоида, м;

α - сжатие эллипсоида.

Для преобразования пространственных прямоугольных координат в геодезические выполняется итерационная процедура вычисления геодезической широты и геодезической высоты:

1) вычисляют вспомогательную величину D по формуле:

2) если D=0, то

3) если D≠0, то

при этом

4) если Z=0, то

B=0, H=D-a

5) если Z≠0, находят вспомогательные величины r, c, p по формулам и реализуют итеративный процесс:

начало итеративного процесса:

s₁=0

М:

b=c+s₁

если d, меньше установленного значения δ, то

В=b

если d равно или больше установленного значения δ, то

s₁=s₂ и вычисления продолжают, начиная с метки М.

Примечания

1. При преобразованиях координат в качестве допуска δ прекращения итеративного процесса принимают значение 0,0001" (4.848136811·10^-6). В этом случае погрешность вычисления геодезической высоты не превышает 0,003 м.

2. Большая полуось эллипсоида а=6378136 м

Коэффициент сжатия α=1/298,25784.

Для определения угловой ориентации летательного аппарата преобразуем орты системы координат OX_пY_пZ_п из земной системы координат в нормальную (земную) систему координат. Преобразование имеет вид:

где матрица преобразования координат M_N приведена выше.

Для случая, когда система координат пеленгатора повернута относительно связанной системы координат летательного аппарата по курсу на угол Δψ, по тангажу на угол Δθ, по крену на угол Δγ, производится преобразование ортов (см. фиг. 5) из нормальной системы в связанную систему летательного аппарата по формуле:

здесь М_Δ - матрица, определенная следующим образом:

где а₁₁=cosΔθ·cosΔψ

a₂₁=sinΔγ·sinΔψ-cosΔγ·sinΔθ·cosΔψ

a₃₁=sinΔγ·sinΔθ·cosΔψ+cosΔγ·sinΔψ

a₁₂=sinΔθ

a₂₂=cosΔγ·cosΔθ

a₃₂=-sinΔγ·cosΔθ

a₁₃=-cosΔθ·sinΔψ

а₂₃=cosΔγ·sinΔθ·sinΔψ+sinΔγ·cosΔψ

a₃₃=cosΔγ·cosΔψ-sinΔγ·sinΔθ·sinΔψ

Матрица направляющих косинусов, определяющая разворот связанной с пеленгатором системы координат OX_пY_пZ_п (положительное направление оси ОХ_п совпадает с направлением положительное направление оси OY_п совпадает с направлением а положительное направление оси OZ_п совпадает с направлением ) относительно нормальной (земной) системы координат OX_gY_gZ_g, имеет вид:

где

Углы курса, тангажа и крена летательного аппарата (см. фиг. 6) в нормальной земной системе координат определяются выражениями:

ψ=-arctg2(c₁₁,c_3l)

θ=arcsin(c₂₁)

γ=-arctg2(c₂₂,c₂₃)

Проведенное математическое моделирование подтвердило эффективность предлагаемого способа определения угловой ориентации в среде глобальных радионавигационных систем.

Источники информации

1. УДК 621.396.96:629.783 Сетевые спутниковые радионавигационные системы / B.C. Шибшаевич, П.П. Дмитриев, Н.В. Иванцевич, и др.; Под ред. B.C. Шибшаевича, - 2-е изд., перераб. и доп. - М.; Радио и связь, 1993. - 408 с.: ил. - ISBN 5-526-00174-4, стр. 205).

2. Патент №2185637, Российская Федерация. Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем (варианты) / Алешечкин A.M., Кокорин В.И., Фатеев Ю.Л. // Опубл. 2002, бюл. №20.

3. Патент №2379700, Российская Федерация. Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем / Алешечкин A.M., Кокорин В.И., Фатеев Ю.Л. // Опубл. 2010, бюл. №2.

4. Патент №2446410, Российская Федерация. Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем / Алешечкин А.М. // Опубл. 27.03.2012.

5. ГОСТ 20058-80 Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения. Издательство стандартов, 1981.

Способ определения угловой ориентации летательного аппарата, при котором принимают сигналы от космических аппаратов глобальных радионавигационных систем на разнесенные антенны количеством не менее трех, измеряют фазовые сдвиги между принятыми сигналами от каждого космического аппарата, подбирают значения целочисленных неоднозначностей измерений фазовых сдвигов, определяют угловую ориентацию из условия максимума функции правдоподобия,отличающийся тем, что антенны расположены на летательном аппарате не на одной прямой, а подбор значений параметров фазовой неоднозначности осуществляют только для случаев осуществимых пеленгаций космических аппаратов, при этом значения угловой ориентации определяют с учетом положения космических аппаратов, векторов, соединяющих антенны, пеленгов космических аппаратов и их взаимной связи: где i, j - номера космических аппаратов (КА), при этом i≠j;Δθ_i,j - угол между векторами, образованными линиями, соединяющими объект и космические аппараты с номерами i, j;Ω - угол между векторами, образованными линиями, соединяющими антенны и образующими первую и вторую базы пеленгатора; - пеленг космического аппарата номер i на первой базе; - пеленг космического аппарата номер i на второй базе; - пеленг космического аппарата номер j на первой базе; - пеленг космического аппарата номер j на второй базе;для условия выражения связи для пеленгов: для условия выражения связи для пеленгов: