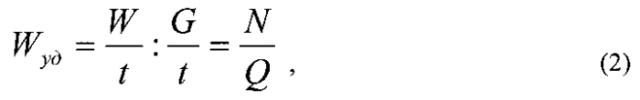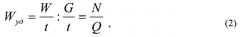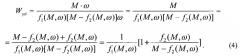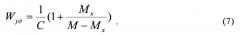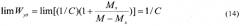Способ минимизации энергоемкости машины непрерывного действия на основе комплексного анализа экспериментальных исследований её прототипа

Способ минимизации энергоемкости машины непрерывного действия на основе комплексного анализа экспериментальных исследований её прототипа

Иллюстрации

Показать все

Реферат

Изобретение относится к области повышения энергетической эффективности машин различного назначения, в первую очередь применительно к машинам, оборудованным активным рабочим органом непрерывного действия, который имеет возможность изменять нагрузочный режим в процессе выполнения технологической операции. В частности, такими объектами минимизации энергозатрат являются машины с отделяющим органом (фреза, цепной бар, рабочий орган многоковшового экскаватора и т.п.), обрабатывающим органом (рабочий орган для измельчения, дробления материала и т.п.), транспортирующим органом (скребковый транспортер, ленточный транспортер, отделяющий цепной транспортер и т.п.).

Одной из причин неэффективности энергетических показателей существующих машин является отсутствие методик их комплексного энергетического анализа, где машина представлялась бы в виде энергетического объекта, объединяющего в единое целое силовую установку, трансмиссию и рабочий орган. В связи с этим в настоящее время разработчики приводных двигателей (электрических машин и двигателей внутреннего сгорания), специалисты по конструированию узлов и деталей передаточных механизмов и создатели рабочих органов анализируют энергетические параметры машины только в рамках своей специализации. В результате несогласованность конструкторских решений специалистов различного профиля в конечном итоге негативно отражается на энергетических характеристиках разрабатываемых машин в целом [1, 2].

Ввиду отсутствия детерминированных зависимостей, увязывающих между собой все три компонента машины, в машиностроении применяют методы пассивного прогноза (например, метод аппроксимации [3]). Однако такие методы пассивного (статистического) прогноза не позволяют получать проектируемую машину с оптимальными энергетическими параметрами.

В работах автора [2, 4] выполнено теоретическое и экспериментальное обоснование комплексного энергетического анализа машинных агрегатов. При этом машина представляется как энергетический объект, объединяющий в единое целое три компонента: энергоустановку, трансмиссию, рабочий орган. Благодаря комплексному подходу установлены необходимые детерминированные связи между указанными компонентами машины.

Установленные автором [2, 4] зависимости послужили основанием для разработки предлагаемого способа определения энергетически рациональных параметров машины. Способ минимизации энергопотребления машин непрерывного действия, описанный в [2], является наиболее близким к предлагаемому изобретению.

Технический результат достигается благодаря тому, что сначала проводят экспериментальные исследования прототипа машины и устанавливают энергетические характеристики рабочего органа и трансмиссии. Затем на их основе с учетом детерминированных связей подбирают соответствующие режимные параметры приводного двигателя, которые обеспечивают минимизацию удельных затрат энергии на единицу продукции, производимой машиной, тем самым существенно снижают ее энергоемкость.

Теоретические основы способа

Показатель энергоемкости W_уд широко используют в инженерной практике для сравнительной оценки энергетической эффективности транспортирующих, обрабатывающих механизмов и машин с отделяющим рабочим органом одного назначения:

где G - количество транспортируемого (обрабатываемого и т.п.) материала, определяемого массой, весом, объемом и т.п.; W - потребляемая механизмом энергия, необходимая для транспортирования (обработки) G количества материала.

Представляют этот показатель также и в другом виде:

где t - промежуток времени, за который транспортировалось (обрабатывалось) G материала; N - мощность приводного двигателя, необходимая для совершения технологического процесса; Q - производительность механизма, то есть количество транспортируемого (обрабатываемого) материала в единицу времени.

Несмотря на популярность этого энергетического показателя, его информационные возможности до настоящего времени используются весьма ограниченно. С целью расширения такой возможности введем новые характеристики и выполним подробный анализ влияния всех факторов на величину W_уд.

Производительность машины можно представить как функцию полезной мощности:

где Ν_пол - полезная мощность (мощность на рабочем органе); f₁(M,·ω) - коэффициент, зависящий от крутящего момента Μ и частоты ω вращения приводного вала; f₁(Μ, ω) выражается массой (объемом) транспортируемого (обрабатываемого) материала, отнесенной к единице затраченной полезной энергии. Другими словами, этот коэффициент характеризует способность рабочего органа конвертировать энергию в продукцию. В дальнейшем будем именовать его коэффициентом качества рабочих органов.

Для анализа используем также зависимости: N=Μω; N_пол=M_полω; M_пол=М-М_c; М_c=f₂(M, ω), где M_пол - полезный крутящий момент, приведенный к приводному валу; М_с - момент сопротивления трансмиссии прокручиванию (определяет величину фрикционных потерь в трансмиссии, то есть характеризует ее энергоемкость).

С учетом указанных зависимостей модернизируем выражение энергоемкости (2):

Из полученной закономерности (4) следует, что энергоемкость транспортирующего (обрабатывающего) устройства непрерывного действия обратно пропорциональна нагрузке (крутящему моменту М) на приводном валу двигателя и зависит от коэффициента качества рабочих органов и энергетической характеристики трансмиссии, определяемой ее моментом сопротивления прокручиванию. При этом очевиден тот факт, что изменение скоростного режима машины оказывает на энергоемкость только косвенное влияние.

Зависимость (4) обеспечивает возможность комплексного энергетического анализа машины, так как учитывает взаимное влияние на энергоемкость всех трех ее компонентов.

Выражение (4) является универсальным, т.е. применимо для анализа любых механизмов непрерывного действия. Однако предлагаемый способ имеет ограничение: он распространяется только на определенную выше группу машин, для которых характерны следующие особенности:

- коэффициент качества рабочих органов практически не зависит от нагрузочного и скоростного режимов:

- момент сопротивления трансмиссии может быть принят постоянным и равным моменту Μ_x прокручивания трансмиссии на холостом ходу:

Тогда зависимость (4) принимает вид гиперболы:

В результате обработки автором экспериментальных исследований, проведенных разными исследователями независимо друг от друга на абсолютно различных по своей конструкции устройствах (роторные и цепные экскаваторы, почвенные и болотные фрезы, погрузчики силоса, кормораздатчики и др. [5, 6, 7]), было выявлено существование группы машин, обладающих постоянством коэффициента качества рабочих органов и практически неизменным от режимных параметров привода моментом сопротивления трансмиссии прокручиванию; изменение энергоемкости данных машин подчиняется закономерности (7).

На основании (3) записываем уравнение производительности таких машин:

Система уравнений (7) и (8) увязывает между собой все энергетические характеристики данных машин: W_уд, Q, M, M_x, ω, C. Эта связь представлена графически на фиг. 1, где 1 - зависимость W_уд=1/C[1+M_x/(M-M_x)]; 2 - зависимости Q=C·ω_i·(M-M_x) при различных значениях ω_i. A_ГР - такая точка на гиперболе W_уд=f(M), движение от которой вправо по кривой (то есть в сторону увеличения параметра (M) практически не приводит к снижению энергоемкости. Значение ординаты в данной точке определим значением M_ГР (фиг. 1).

График, представленный на фиг. 1, демонстрирует, что одна и та же заданная производительность Q_ЗАД механизма может быть получена при различных скоростных и нагрузочных режимах приводного двигателя. При этом менее энергоемким будет тот механизм, который при прочих равных условиях обеспечит заданную производительность при большем крутящем моменте на приводном валу и наименьшей частоте его вращения (ω₁>ω₂>ω₃).

Предварительные экспериментальные исследования на прототипе машины позволяют:

- при заданной частоте ω вращения приводного вала двигателя установить энергетические характеристики машины: коэффициент С качества рабочего органа и момент М_x холостого хода трансмиссии;

- определить функциональную зависимость энергоемкости машины от нагрузочного момента W_уд=f(M) и представить ее в виде графика;

- определить граничное значение крутящего момента M_гр на приводном валу, при наличии которого исключается возможность попадания машины в область «дограничных» нагрузочных режимов, характеризующихся большими энергозатратами на единицу продукции.

Для реального использования зависимостей (7) и (8) необходимо фиксировать величину крутящего момента на приводном валу. Для этой цели применяют три приема.

1. Метод тензометрирования приводного вала. Этот метод универсален и может быть использован при любом типе приводного двигателя, но весьма трудоемок.

2. Метод измерения электрической мощности приводного двигателя. Этот метод приемлем при использовании приводных электродвигателей, имеющих жесткую механическую характеристику (синхронные и асинхронные двигатели переменного тока, двигатели постоянного тока параллельного возбуждения, электродвигатели с импульсной системой регулирования частоты). При условии постоянной частоты вращения легко устанавливается связь между механической N и электрической P мощностями двигателя: Ν=Μω=η_ДP, где η_Д - КПД, определяющий величину электрических потерь в электродвигателе. При заданной частоте вращения искомый крутящий момент определяется на основе электрической мощности, измеренной ваттметром. Тогда M=η_ДP/ω. Это существенно упрощает проведение измерительных работ по сравнению с первым методом.

3. Метод нагружения приводного двигателя за счет контролируемого изменения нагрузки на рабочем органе. Этот метод наиболее удобен для испытания прототипа в естественных (полевых) условиях взаимодействия со средой, что следует признать большим преимуществом в сравнении с испытаниями в лабораторных условиях. Ниже приведены зависимости, определяющие данный метод испытаний.

При проведении исследований в полевых условиях энергетические показатели N, Q, W_уд представляют в виде функции от величины H, определяющей степень взаимодействия рабочего органа со средой (материалом). Суть параметра H можно определить величиной подачи рабочего органа относительно взаимодействующей с ним среды. В одних случаях это толщина срезаемой стружки, в других - величина внедрения в материал рабочего органа, что практически равноценно. Могут быть и другие интерпретации этого параметра (например, для пильных цепей электрических и бензомоторных пил определяющим параметром оказывается величина усилия прижатия рабочего органа к материалу [8]). Однако во всех случаях H представляет собой меру степени загрузки рабочего органа и, следовательно, равноценен величине полезного крутящего момента на рабочем органе

Последовательность экспериментальных испытаний прототипа путем контролируемого нагружения рабочего органа в полевых условиях

Нагружают рабочий орган, пошагово изменяя величину H. В каждом опыте измеряют производительность машины и мощность на приводном валу. В результате получают два массива экспериментальных значений: Q=f(H) и N=f(H) (фиг. 2). Используя метод наименьших квадратов [9, 10], аппроксимируют экспериментальные точки обеих зависимостей. На фиг. 2: 3 - зависимость (10), 4 - зависимость - (11), 5 - зависимость - (13).

где B, B₁, N_х - константы аппроксимирующих функций. При этом N_х - величина мощности холостого хода машины, которая может быть определена не только в результате аппроксимации массива экспериментальных данных, но и путем прокручивания трансмиссии машины при отсутствии нагрузки на рабочем органе.

При выполнении аппроксимации оценивают ее достоверность. Для этой цели вычисляют относительную ошибку D измерений с учетом t - распределения Стьюдента [11]:

где σ - величина среднего квадратичного отклонения ординат экспериментальных точек от теоретических значений; n - количество экспериментальных точек; H ¯ - среднее арифметическое (математическое ожидание) экспериментальных значений H.

В инженерных расчетах допустимо принимать доверительный интервал в пределах 10% [11]. Если значение относительной ошибки D существенно превышает данную величину, то это указывает: а) либо на недостаточность числа экспериментальных точек, б) либо на несоответствие выбранного вида аппроксимирующей функции. В последнем случае следует отказаться от использования предлагаемого способа.

На основании (2), (10), (11) имеем:

где A и A₁ - константы.

Следовательно, функция W_уд=f(H) также является гиперболической зависимостью (фиг. 2).

Следует подчеркнуть, что функциональные зависимости Q=f(H) и N=f(H) получают при практическом постоянстве скоростного режима, что необходимо четко фиксировать. Дело в том, что имеется возможность расширить область применения способа для машин, у которых скоростной режим оказывает влияние на коэффициент качества рабочего органа. При этом методика остается прежней, только увеличивается количество испытаний при различных значениях ω.

С учетом условия (9) сопоставим предельные значения W_уд, получаемые на основании формул (7) и (13).

Μ→∝ M→∝

H→∝ H→∝

Следовательно, константа A есть не что иное, как обратная величина коэффициента качества: A=1/C.

Из уравнения (11) следует, что полезная мощность N_пол равна N_пол=B₁·H.

После аппроксимации экспериментальных данных, полученных путем естественного нагружения рабочего органа (функции (10), (11)), имеем возможность перейти к энергетическому анализу на основе закономерности (7):

- вычисляем величину обратную коэффициенту качества: ;

- определяем момент холостого хода трансмиссии: Ν_Х/ω=М_Х;

- представляем результаты исследований в виде зависимости (7) (фиг. 1).

В работе [2] доказано, что на гиперболической зависимости (7) может быть определено такое граничное значение аргумента M_ГР, при котором значение величина W_уд стабилизируется в пределах не превышающих величину 1/C на 10%. Эта величина вычисляется по формуле

Обоснование величины граничных значений крутящего момента и мощности на приводном валу двигателя

Представим новый подход к определению величины M_ГР, который существенно упрощает его определение, а следовательно, минимизирует вычислительные операции, ускоряет реализацию способа и расширяет возможности его широкого применения в инженерной практике.

Граничное значение энергоемкости W_у∂ГР принимают в пределах 10-процентного доверительного интервала (см. выше), т.е., другими словами, можно считать, что W_у∂ГР превышает минимально достижимую величину энергоемкости, равную А=1/С, на 10% (см. фиг. 1):

W у ∂ Г Р = 1,1 ( 1 / С ) .           ( 16 )

Решение системы уравнений (7) и (16) позволяет определить величину граничного крутящего момента:

Следовательно, мощность приводного двигателя, соответствующая требованиям минимизации энергоемкости, должна составлять:

N Г Р ≥ 11 M x ⋅ ω           ( 18 )

Условия (16), (17), (18) существенно упрощают выбор режимных параметров приводного двигателя, исключающих работу машины в неэкономичных (дограничных) нагрузочных режимах. А именно: если исследователь обладает надежной информацией о том, что коэффициент качества рабочих органов имеет стабильное значение в рабочих скоростных и нагрузочных режимах, то для выбора граничной (то есть минимально необходимой) мощности приводного двигателя достаточно методом прокручивания установить мощность холостого хода трансмиссии машины, а затем вычислить граничное значение мощности двигателя, приняв ее равной мощности холостого хода трансмиссии, увеличенной в 11 раз. При этом, естественно, частота вращения двигателя остается равной заданной, а реализация расчетной мощности обеспечивается исключительно за счет соответствующего нагружения рабочего органа.

СПИСОК ЛИТЕРАТУРЫ

1. Александров, И.К. Совершенствование сельскохозяйственных машин и агрегатов на основе энергетического анализа: дис. … д-ра техн. наук / И.К. Александров. - СПб.: СПбГАУ, 1993. - 414 с.

2. Александров, И.К. Энергетический анализ механизмов и машин. Теоретическое и экспериментальное обоснование принципов исследования и определения энергетических потерь в механизмах и машинах: монография / И.К. Александров. - 2 изд., испр. и доп. - Вологда: ВоГТУ, 2012. - 244 с.

3. Домбровский, Н.Г. Строительные машины: учебник для специальности вузов "Строит. и дор. машины и оборудование" Ч. 1 / Н.Г. Домбровский, Ю.Л. Картвелишвили, М.И. Гальперин. - М.: Машиностроение, 1976. - 391 с.

4. Александров, И.К. Энергосбережение в машинных агрегатах (основы энергетического анализа, пути снижения энергоемкости машин и механизмов) / И.К. Александров. - Вологда: Сев.-Двинское отдел. инженерной академии РФ, 1993. - 192 с.

5. Алексеева, Т.В. Машины для земляных работ / Т.В. Алексеева, К.А. Артемьев, А.А. Бромберг. - М.: Машиностроение, 1964. - 567 с.

6. Кутлембетов, А.А. Исследование процесса отделения силоса от общей массы рабочими органами погрузчиков непрерывного действия: Автореф. дис. … канд. техн. наук / А.А. Кутлембетов. - М., 1969. - 20 с.

7. Петлах, Я. Выбор экономичных технологий для первичного освоения болот и заболоченных земель / Я. Петлах, А. Лукьянов, В. Пятковский // Техника в сельском хозяйстве. - 1971. - №1. - С. 24-26.

8. Александров, И.К. Методика определения топливной экономичности бензиномоторных пил / И.К. Александров, И.В. Григорьев // Деловой журнал «Дерево.ru». - 2010. - №1. - С. 48-51.

9. Корн, Г. Справочник по математике (для научных работников и инженеров) / Г. Корн, Т. Корн. - М.: Наука, 1973. - 831 с.

10. Лопатников, Л.И. Экономико-математический словарь: Словарь современной экономической науки / Л.И. Лопатников. - 5-е изд., перераб. и доп. - М.: Дело, - 2003. - 520 с.

11. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. - М.: Высшая школа, 1977. - 479 с.

1. Способ минимизации энергоемкости машины, оборудованной рабочим органом непрерывного действия, на основе комплексного энергетического анализа экспериментальных исследований ее прототипа, заключающийся в том, что предварительно экспериментальным путем на прототипе, пошагово изменяя величину Н, определяющую степень взаимодействия рабочего органа со средой, при заданной частоте вращения ω приводного вала устанавливают два массива экспериментальных значений: производительности Q в функции от Н (Q=ƒ(H)) и механической мощности N на выходном валу приводного электродвигателя в функции от Н (N=ƒ(H)); используя метод наименьших квадратов, аппроксимируют данные массивы соответственно линейными зависимостями:Q=B·HиN=В₁·Н+N_X,где В, B₁, N_X - константы аппроксимирующих функций;используя соотношение B 1 B = 1 / C , находят величину, обратную коэффициенту качества рабочих органов 1/С; вычисляют момент M_X холостого хода трансмиссии по формулеM_X=N_X/ω;представляют энергоемкость машины в виде зависимости: W у ∂ = 1 C ( 1 + M x M − M x ) ,где М - текущее значение крутящего момента на валу двигателя; вычисляют величину граничного момента на валу приводного двигателя по формуле M Г Р = 0,563 M x C + M x ,при реализации которой исключается работа машины на энергетически неэффективных нагрузочных режимах, отличающийся тем, что принимают граничное значение энергоемкости машины равным W_у∂ГР=1,1(1/С) и вычисляют граничную мощность приводного двигателя по формулеN_ГР=11M_X·ω.

2. Способ по п. 1, отличающийся тем, что величину M_X устанавливают на основе тензометрирования приводного вала двигателя.